1.Floyed算法
1.1适用范围
∙ \bullet ∙ 求每队顶点的最短路径
∙ \bullet ∙ 有向图、无向图和混合图
1.2算法思想
直接在图的带权邻接矩阵中用插入顶点的方法依次递推地构造出n个矩阵D(1),D(2)…D(n)(每次加入一个点然后更新最短路径矩阵D),D(n)是图的最短距离矩阵,同时引入一个后继点矩阵path记录两点间的最短路径。
1.3实例
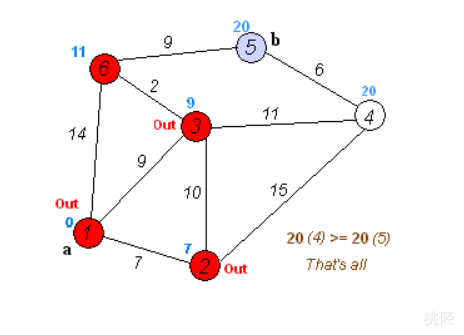
对于如下无向图:
我们可以得如下带权邻接矩阵:
[
0
7
9
i
n
f
i
n
f
14
7
0
10
15
i
n
f
i
n
f
9
10
0
11
i
n
f
2
i
n
f
15
11
0
6
i
n
f
i
n
f
i
n
f
i
n
f
6
0
9
14
i
n
f
2
i
n
f
9
0
]
\begin{bmatrix} 0 & 7 & 9 & inf & inf & 14\\ 7 & 0 & 10 &15 & inf & inf\\ 9 & 10 & 0 & 11 & inf & 2\\ inf & 15 & 11 & 0 & 6 & inf\\ inf & inf & inf & 6 & 0 & 9\\ 14 & inf & 2 & inf & 9 & 0\\ \end{bmatrix}
⎣⎢⎢⎢⎢⎢⎢⎡079infinf14701015infinf910011inf2inf151106infinfinfinf60914inf2inf90⎦⎥⎥⎥⎥⎥⎥⎤
实现步骤:
∙ \bullet ∙ 变量:输入变量与输出变量
| 输入变量 | 含义 |
|---|---|
| w矩阵 | 带权邻接矩阵 |
| start | 初始点 |
| terminal | 终止点 |
| 输出变量 | 含义 |
|---|---|
| D矩阵 | D(i,j)表示i到j的最短路径 |
| path矩阵 | path(i,j)表示i到j之间的最短路径上顶点i的后继点 |
| min1 | start与terminal之间的最短距离 |
| path1 | start与terminal之间的最短路径 |
∙ \bullet ∙ 赋初值:对所有的i、j, D ( i , j ) = w ( i , j ) , p a t h ( i , j ) = j , k = 1 ( k 表 示 加 入 的 顶 点 个 数 ) D(i,j)=w(i,j),path(i,j)=j,k=1(k表示加入的顶点个数) D(i,j)=w(i,j),path(i,j)=j,k=1(k表示加入的顶点个数)
∙
\bullet
∙ 更新D(i,j)、path(i,j),对于所有i、j,若
D
(
i
,
k
)
+
D
(
k
,
j
)
<
D
(
i
,
j
)
D(i,k)+D(k,j)<D(i,j)
D(i,k)+D(k,j)<D(i,j)
则:
D
(
i
,
j
)
=
D
(
i
,
k
)
+
D
(
k
,
j
)
,
p
a
t
h
(
i
,
j
)
=
p
a
t
h
(
i
,
k
)
,
k
=
k
+
1
D(i,j)=D(i,k)+D(k,j), path(i,j)=path(i,k),k=k+1
D(i,j)=D(i,k)+D(k,j),path(i,j)=path(i,k),k=k+1
∙
\bullet
∙ 每次插入一个顶点重复进行更新操作,直到 k=n+1 终止。
2.代码
2.1floyd函数
function [D,path,min1,path1]=floyd(a,start,terminal)
%D(i,j)表示i到j的最短路径,path(i,j)表示i到j之间的最短路径上顶点i的后继点。
%min1返回start和terminal之间的最短距离,path1返回start和terminal之间的最短路径
%a为带权邻接矩阵,start、terminal分别是起始点和终止点
D=a;n=size(D,1);path=zeros(n,n);
%n为顶点个数,生成D、path矩阵
%遍历一遍矩阵,初始化path矩阵,先将可以直接相连的点的path进行补充
for i=1:n
for j=1:n
if D(i,j)~=inf
path(i,j)=j;
end
end
end
%三重遍历,查找是否有中继点可以使得路径缩短,若有则更新D、path矩阵
for k=1:n
for i=1:n
for j=1:n
if D(i,k)+D(k,j)<D(i,j)
D(i,j)=D(i,k)+D(k,j);
path(i,j)=path(i,k);
end
end
end
%这里演示了每一步的调整过程
k,D,path
end
%判断输出参数是否为三个
if nargin==3
min1=D(start,terminal);
m(1)=start;
i=1;
path1=[ ];
%根据path路径一步一步跳转找到具体路径,返回path1
while path(m(i),terminal)~=terminal
k=i+1;
m(k)=path(m(i),terminal);
i=i+1;
end
m(i+1)=terminal;
path1=m;
end
2.2调用函数
w = [0,7,9,inf,inf,14;
7,0,10,15,inf,inf;
9,10,0,11,inf,2;
inf,15,11,0,6,inf;
inf,inf,inf,6,0,9;
14,inf,2,inf,9,0];
start=1;terminal=5;
[D,path,min,path1]=floyd(w,start,terminal);
D,path,min,path1
结果:
这里介绍一下如何看path矩阵查找最短路径:比如说要查找1到5的最短路径
∙ \bullet ∙ 那么我们就要找 path(1,5)=3,所以目前路径为1->3
∙ \bullet ∙ 接着我们就要找 path(3,5)=6,所以目前路径为1->3->6
∙ \bullet ∙ 接着我们就要找 path(6,5)=5,到达终点,所以最终路径为1->3->6->5
注意:调用floyd函数的时候,同时还会输出每次插入一个顶点之后D矩阵和path矩阵的变化。