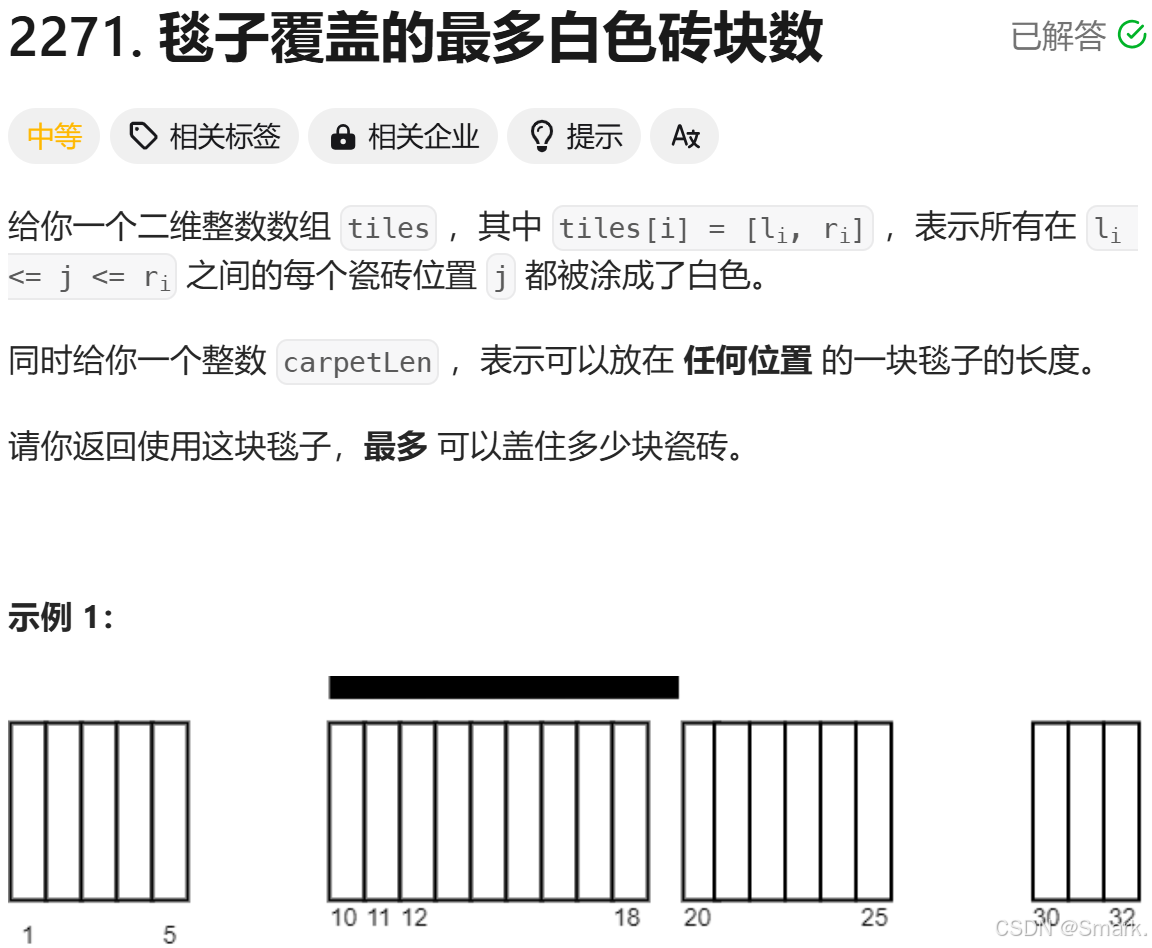
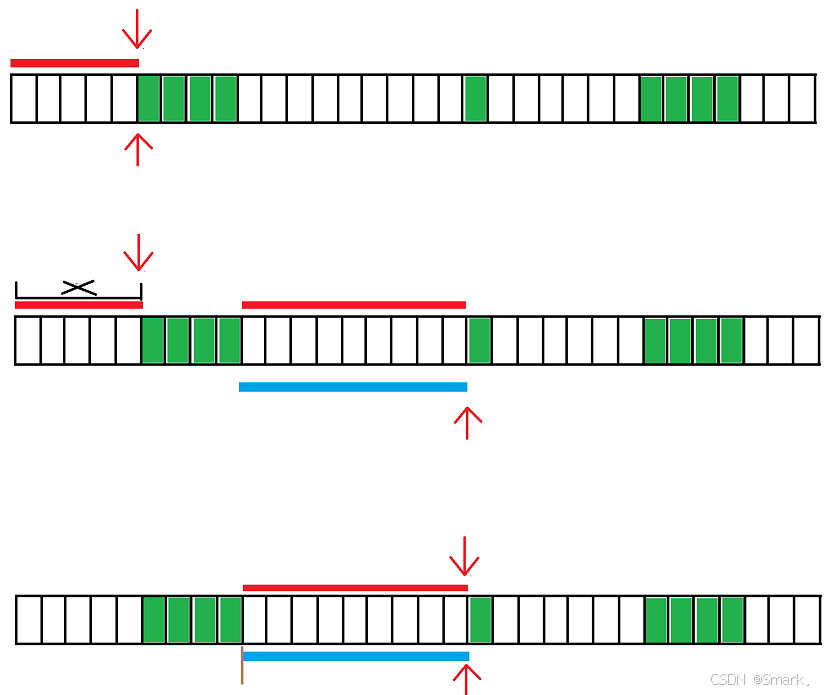
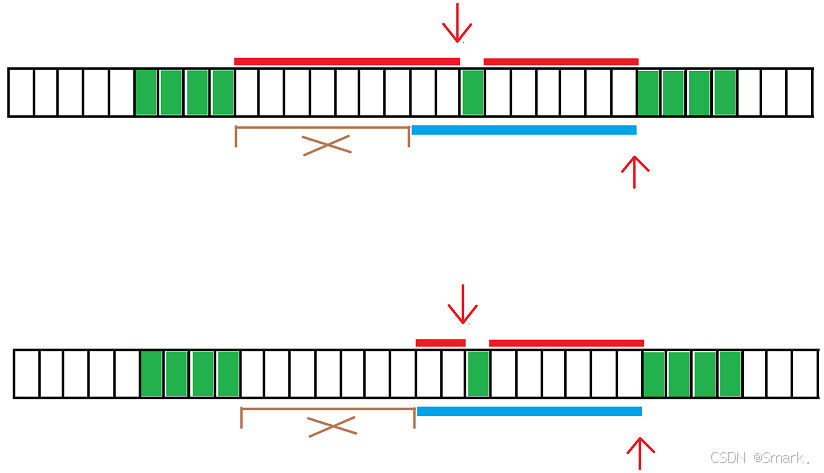
滑动窗口的窗口长度固定,那么其研究的窗口所在位置一定是通过画图遍历,这样能够快速的分析问题,直接围绕这些特殊的位置求解固定长度的滑动窗口问题
h
下面说明只研究一种状态的窗口,
将窗口的右端点,放在tiles中每个瓷砖的右端点来确定每一个状态,
从图中可以看出,之所以这么选,是因为中间的把蓝条(毯子)的右端点放到瓷砖的右端点,其覆盖的瓷砖的长度总是大于等于把蓝条(毯子的右端点)放到瓷砖的中间,
注意:这里的l 和 r 应该作为tiles的下标,那么l和r在不同位置时代表什么含义?
case1: l == r - k (k > 0)
此时代表将 l 指向的 tile, l + 1, ... l + k 指向的tile都作为窗口中的内容,不会考虑绿色区域
case2: l == r
此时代表 只考虑将 r 指向的 tile作为窗口中的内容
这个题目需要问以下几个问题
Q1. 什么情况需要考虑开始从 r 所指的位置循环执行进窗口动作?
r 遍历到的当前tiles, 需要不断进窗口
Q2. 什么时候需要暂停执行进窗口动作?
r 遍历到的当前tiles, 需要不断进窗口
Q3. 什么时候需要考虑开始从 l 所指的位置循环执行出窗口动作?
l 指向的tiles 的右端点 大于 r指向的tiles的右端点 - 毯子的长度 + 1
Q4. 什么时候需要暂停执行出窗口动作?
l 指向的tiles 的右端点 小于等于 r指向的tiles的右端点 - 毯子的长度 + 1
Q5. 什么时候更新结果?
每次进窗口动作执行一次之后,执行以下逻辑来更新结果
首先,判断出窗口,
如果对 l 指向的 tiles 进行出窗口,那么 l 每出一个窗口,
就用结果将当前的 l 指向的tiles的长度给减去
其次,在出窗口暂停后,
如果 毯子从 r 所指向的 tiles的右端点无法覆盖完 l 所指向的 tiles 的左端点
那么用结果将 减去 α,其中α分两种情况
case1: r 指向的tiles的右端点 - 毯子的长度 > l 所指向的 tiles 的左端点,也就是说毯子右端
点在r 指向的右端点,左端点在l 所指向的 tiles 的中间
此时 α = r 指向的tiles的右端点 - 毯子的长度 - l 所指向的 tiles 的左端点 + 1
case2: r 指向的tiles的右端点 - 毯子的长度 < l 所指向的 tiles 的左端点,也就是说毯子右端
点在r 指向的右端点,左端点在l 所指向的 tiles 的左端点的左边,但是不在 l - 1 所指
向的tiles 的右端点的左边,此时 α = 0
以tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 9为例(注意和原题示例不同)
下图中黑色叉号表明的是出窗口要删除的瓷砖长度,
棕色叉号表明的是当蓝色的毯子盖不住从 l 指向tiles的左端点到l指向的tiles的右端点时,需要删除的长度
// 3413. 收集连续 K 个袋子可以获得的最多硬币数量 和 2271. 毯子覆盖的最多白色砖块数
// 用相同的滑动窗口算法
class Solution {
public:
int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
int n = tiles.size();
sort(tiles.begin(), tiles.end(), [&](vector<int>& v1, vector<int>& v2){
return v1[0] < v2[0];
});
int ret = 0, left = 0, curlen = 0;
for(int i = 0; i < n; ++i){
int tl = tiles[i][0], tr = tiles[i][1];
curlen += (tr - tl + 1);
while(tiles[left][1] < tr - carpetLen + 1){
curlen -= (tiles[left][1] - tiles[left][0] + 1);
left++;
}
int uncover = max(0, tr - carpetLen - tiles[left][0] + 1);
ret = max(ret, curlen - uncover);
}
return ret;
}
};