Gurobi基础语法之 addConstr, addConstrs, addQConstr, addMQConstr

在新版本的 Gurobi 中，向 addConstr 这个方法中传入一个 TempConstr 对象，在模型中就会根据这个对象生成一个约束。更重要的是：TempConstr 对象可以传给所有addConstr系列方法，所以下面先介绍 TempConstr 对象

TempConstr

TempConstr 类的对象作为约束条件，其对象可以有以下几种形式：

1. 线性约束：x + y <= 5

2. 带上下界的线性约束：1 <= x + y <= 5

3. 二次约束：x * x + y * y <= 3

4. 用矩阵建立的线性约束：A @ x <= 1

5. 二次型约束：x @ Q @ x <= y @ A @ y

6. 带绝对值的函数的约束：x == abs_(y)

7. 带逻辑运算符的约束：x == or_(y, z) 或者 x == and_(y, z)

8. 带最大值或最小值函数的约束：x == max_(y, z) 或者 x == min_(y, z)

9. 借助 TempConstr 自定义的运算符 >> 作为表达式中的运算符：(x == 1) >> (y + z <= 5)

有以下几点值得说明：

1. Gurobi 中所有关系运算符都必须带等号，比如 <=, >=, == ，<, >, = 不合法，想要表示小于，例如 x + y < 5 这样的严格不等式约束，可以引入一个很小的值 epsilon，辅助实现严格不等式

2. 上面说的第 7 点中，要求x, y 和 z 都是二元变量，即在添加进模型的时候就设计为GRB.BINARY

3. 上面说的第 9 点中，(x == 1) >> (y + z <= 5) 表达的是，如果 x 为1，则 y + z 必须小于等于5，即 x 这个二元变量控制了后面的不等式约束是否存在

addConstr

Python定义：addConstr(constr, name='')

这个方法的第一个参数就是需要传入 TempConstr 类型的对象

addConstrs

Python定义：addConstrs(generator, name='')

这个方法的第一个参数是 Python 语法中的生成器，也就是说可以传入一个迭代器，通过循环就可以方便的在一行代码中就生成多个约束，下面是这个方法使用的一些例子

m.addConstrs(x.sum(i, '*') <= capacity[i] for i in range(5))
m.addConstrs(x[i] + x[j] <= 1 for i in range(5) for j in range(5))
m.addConstrs(x[i]*x[i] + y[i]*y[i] <= 1 for i in range(5))
m.addConstrs(x.sum(i, '*') == [0, 2] for i in [1, 2, 4])

约束不可能凭空产生，起码需要先添加变量，关于添加变量的方法，已经在我的另外一篇博客 addVar 和 addVars的使用中进行了说明

考虑到读者可能还不是很清楚 Gurobi 中 sum 方法的使用，这已经在我的另外一篇博客tupledict 中的 sum 方法中进行了说明

对于第三个添加的约束，实际上是添加了一个二次约束，对于二次约束，在模型的结果上有很多与线性约束不同的地方，这写不同点已经在我的另外一篇博客带二次约束的模型解构说明中进行了说明

如何建立起一个约束带有上下界的线性优化模型？这在我的另一篇博客中Electricity Market Optimization 探索系列（一）已经进行了说明，

addQConstr

这个方法有两个版本

版本一：addQConstr(lhs, sense=None, rhs=None, name='')

代码示例：

model.addQConstr(x*x + y*y, GRB.LESS_EQUAL, z*z, "c0")

版本二：使用 generator 添加约束

代码示例：

model.addQConstr(x*x + y*y <= 2.0, "c1")

addMQConstr

Python 定义：addMQConstr(Q, c, sense, rhs, xQ_L=None, xQ_R=None, xc=None, name='')

实际上这里使用一个矩阵来定义二次约束，（注意可以不是二次型，而是带有交叉项的二次式）

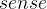
这个二次约束形如 ${x}'_{Q_{L}}Qx_{Q_{R}} + c{}'x_{c}$ sense rhs

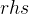
其中sense是一个关系运算符，rhs是一个常数

Q = np.full((2, 3), 1)
xL = model.addMVar(2)
xR = model.addMVar(3)
model.addMQConstr(Q, None, '<', 1.0, xL, xR)