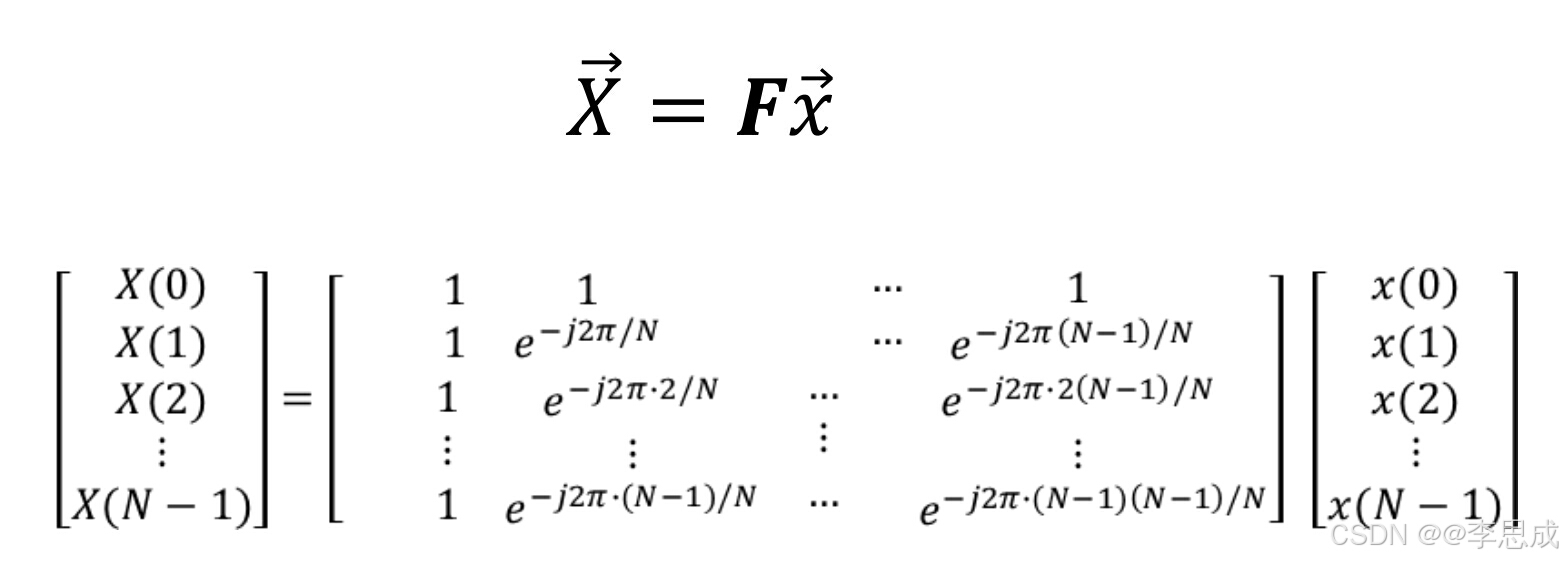语音信号处理及特征提取

一.数字信号处理基础

1.基础知识

模拟信号到数字信号转化（ADC）

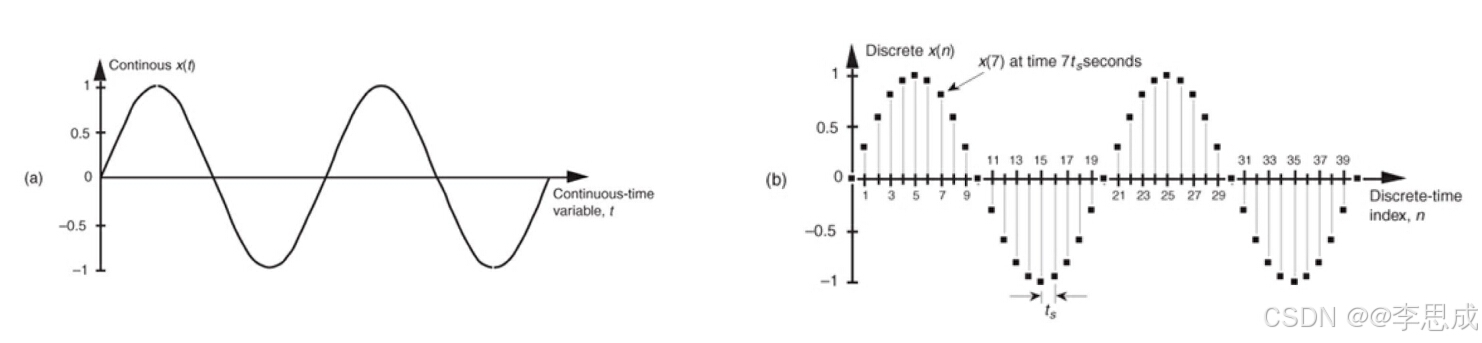
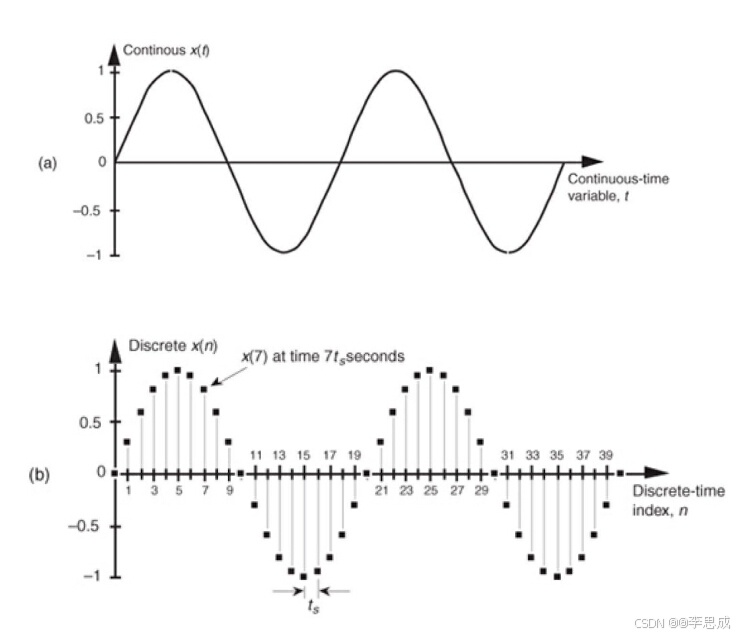
在科学和工程中，大多数信号都是连续的模拟信号，例如电压随时间的变化、一昼夜中的温度变化等。然而，计算机只能处理离散的信号，因此必须对这些连续的模拟信号进行转化。这个转化过程包括采样和量化，将模拟信号转化为数字信号。

以正弦波为例

一个连续的正弦波可以表示为：

$$x(t)=\sin (2\pi f_{0}t)$$

其中 $f_0$为信号的频率，$t$为时间。对该正弦波进行采样时，每隔 $t_s$ 秒进行一次采样，可以得到采样后的离散信号：

$$x(n)=\sin (2\pi f_{0}n{t}_s)$$

其中 $t_s$ 为采样周期，$f_s=\frac{1}{t_s}$ 为采样率，$n$ 为离散序列。

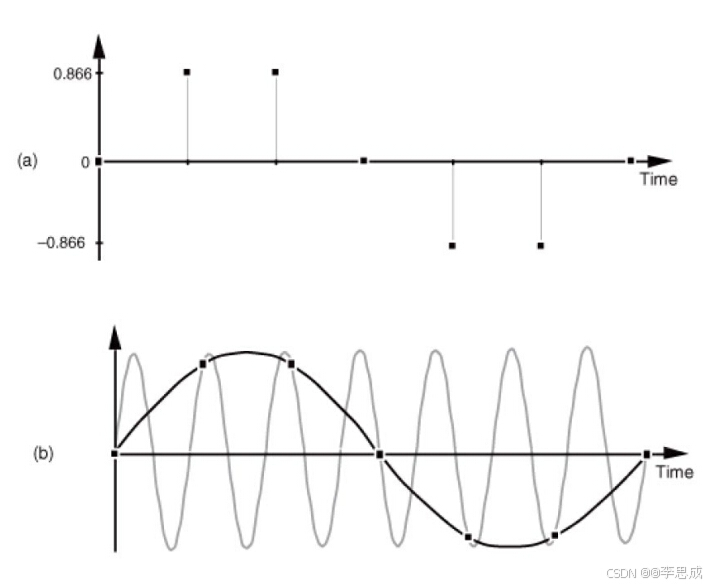
频率混叠

不同频率的正弦波经过采样后可能出现完全相同的离散信号，这种现象称为频率混叠。频率混叠会导致信号无法正确还原，因此需要通过适当的采样率来避免。

奈奎斯特采样定律

奈奎斯特采样定律指出，采样频率必须大于信号中最高频率的两倍，即：

$$f_s>2f_{\text{max}}$$

只有这样，在原始信号的一个周期内，至少要采样两次，才能有效避免频率混叠问题。

2.傅里叶分析

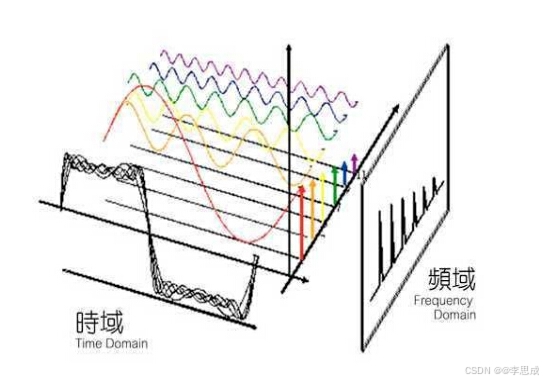
为什么要进行离散傅里叶变换（DFT）？

DFT的作用是将时域信号转换到频域，以分析信号中的频率成分。时域表示信号随时间变化的规律，频域表示信号中的频率成分。在频域中可以更容易地分析和处理信号，特别是当信号包含多个频率成分时。

什么信号可以进行DFT？

时域离散且周期的信号可以直接进行DFT。对于非周期的离散信号，需要通过周期延拓的方法，即将当前信号视为整个信号的一个周期来进行DFT。

什么是DFT？

对于一个长度为 $N$ 的时域离散信号 $x(n)$，其对应的离散频域序列 $X(m)$ 为：

$$X(m)=\sum _{n=0}^{N-1}x(n)e^{-j2\pi nm/N},m=0,1,\dots ,N-1$$

其中 $j=\sqrt{-1}$，$e$ 为自然对数底。根据欧拉公式，DFT的公式还可以表示为：

$$X(m)=\sum _{n=0}^{N-1}x(n)\left[\cos \left(\frac{2\pi nm}{N}\right)-j\sin \left(\frac{2\pi nm}{N}\right)\right]$$

DFT本质上是一个线性变换：

DFT的性质

• 对称性：对于实数信号，有：
  $$X(m)=X^{\ast }(N-m)$$

• 谱密度：对于一个幅度为 $A$ 的正弦波进行 $N$ 点DFT，对应频率上的幅度 $M$ 和 $A$ 之间的关系为：

  $$M=\frac{A}{2N}=\frac{AN}{2}$$

• 线性：DFT的线性，如果 $x_{\text{sum}}(n)=x_1(n)+x_2(n)$，则对应的频域上有：

  $$X_{\text{sum}}(m)=X_1(m)+X_2(m)$$

• 时移性：对 $x(n)$ 左移 $k$ 个采样点，得到的 $x_{\text{shift}}(n)=x(n-k)$，其DFT为：
  $$X_{\text{shift}}(m)=e^{j2\pi km/N}X(m)$$

DFT的频率轴

频率分辨率为 $\frac{f_s}{N}$，表示最小的频率间隔。当 $N$ 越大时，频率分辨率越高。在频域上，第 $m$ 个点表示的频率为：

$$f_{\text{analysis}}(m)=\frac{m}{N}{f}_s$$

3.快速傅里叶变换（FFT）

FFT的基本思想是将原始的 $N$ 点序列分解成一系列短序列，利用DFT计算式中指数因子的对称性质和周期性质，求出这些短序列的DFT并进行适当组合，从而删除重复计算，减少乘法运算，简化结构。

4.推荐教材：

• Understanding DSP，第4章
• 《数字信号处理，理论、算法与实现》，胡广书，清华大学出版社

二.特征提取

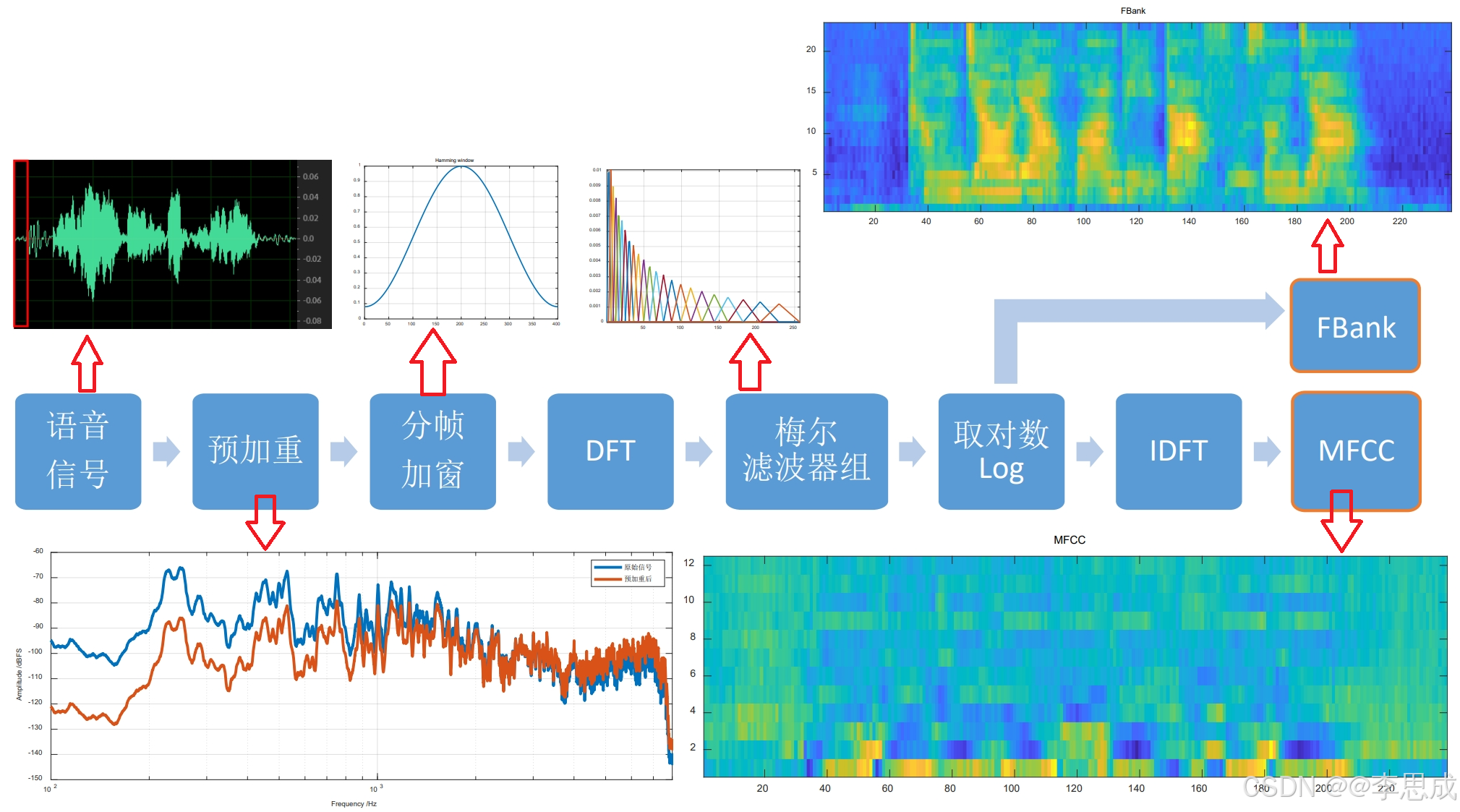
Fbank和MFCC（Mel-Frequency Cepstral Coefficients）提取流程

Fbank和MFCC特征目前仍是主要使用的特征，虽然有工作尝试直接使用波形建模，但是效果并没有超越基于频域的特征

1.预加重

预加重是为了提高信号高频部分的能量。由于高频信号在传递过程中衰减较快，但高频部分又蕴含许多对语音识别有利的特征，因此在特征提取部分，需要提高高频部分的能量。

预加重滤波器是一个一阶高通滤波器。给定时域输入信号 $x[n]$，预加重之后的信号为：$y[n]=x[n]-\alpha x[n-1]$其中，$0.9\le \alpha \le 1.0$。

2.加窗分帧

语音信号是一种非平稳信号，但具有短时平稳的属性。在进行语音识别时，对于一句话，识别的过程也是以较小的发音单元为单位进行识别。因此，用滑动窗来提取短时片段。

对于采样率为16KHz的信号，帧长和帧移一般为25ms和10ms，即400和160个采样点。

分帧的过程即在时域上，用一个窗函数和原始信号相乘。常用的窗函数有矩形窗和汉明窗。加窗的过程实际上是在时域上将信号截断，窗函数与信号在时域相乘，相当于对频域表示进行卷积。矩形窗的主瓣窄，但旁瓣大，将其与原始信号的频域表示卷积，会导致频率泄露。

常用的汉明窗函数定义为：

$$w[n]=0.54-0.46\cos \left(\frac{2\pi n}{L-1}\right)$$

其中，$L$ 为窗长度。

3.傅里叶变换

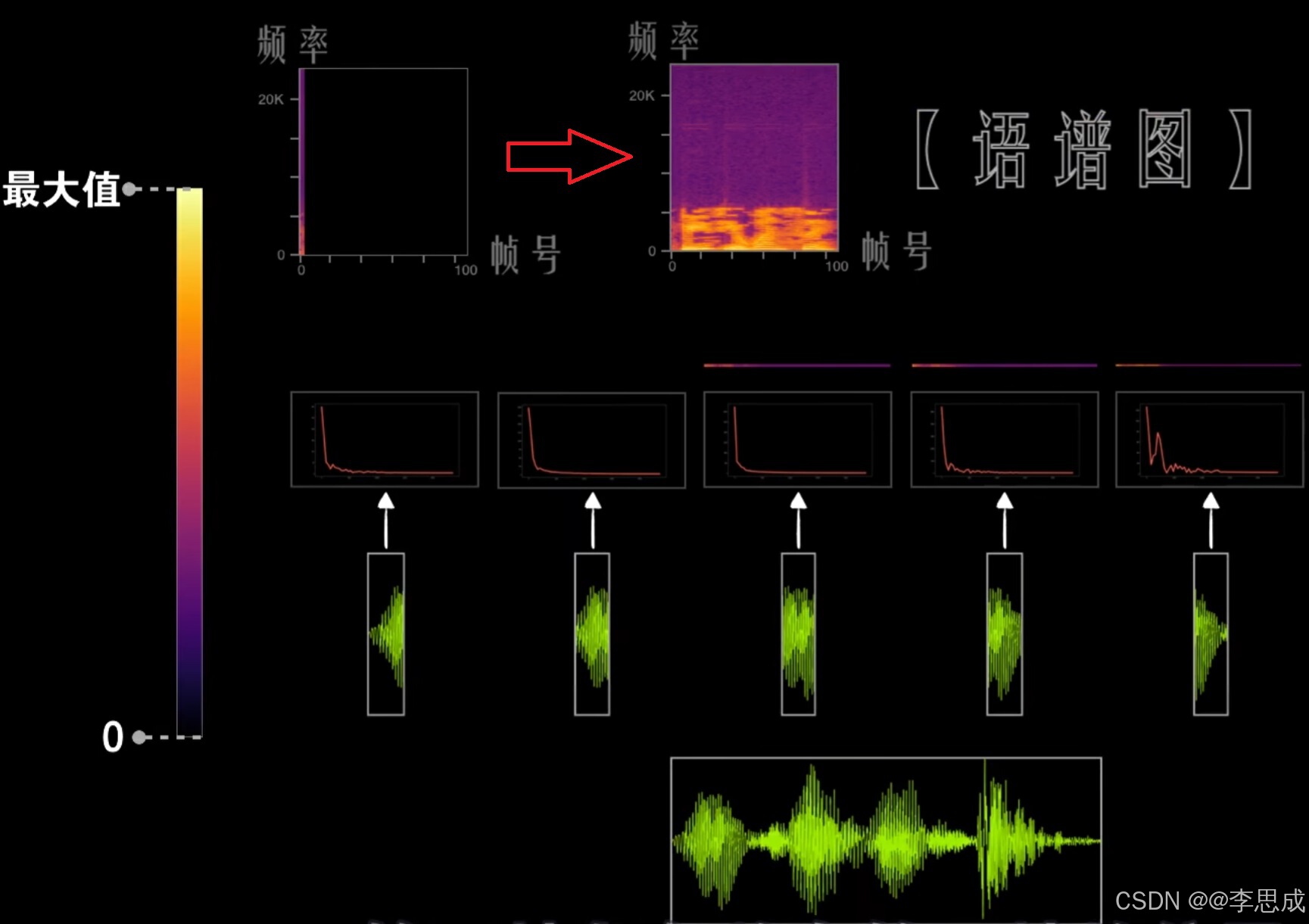
将上一步分帧的语音帧，由时域变换到频域，取DFT系数的模，得到谱特征。具体步骤如下：

1. 对每一帧信号进行DFT（通常使用FFT），将时域信号转换为频域信号。
2. 计算DFT系数的模，得到频域语谱图。

4.梅尔滤波器组及对数操作

梅尔滤波器组是一种符合人耳听觉特性的滤波器组。DFT得到每个频带上的信号能量，但人耳对频率的感知不是等间隔的，近似于对数函数。

将线性频率转换为梅尔频率，梅尔频率和线性频率的转换关系为：

$$\text{mel}(f)=2595{\log }_{10}\left(1+\frac{f}{700}\right)$$

梅尔三角滤波器组可以根据起始频率、中间频率和截止频率确定各滤波器的系数。其设计步骤如下：

1. 确定滤波器组个数 $P$。
2. 根据采样率 $f_s$，DFT点数 $N$ 和滤波器个数 $P$，在梅尔域上等间隔产生每个滤波器的起始频率、中间频率和截止频率。上一个滤波器的中间频率为下一个滤波器的起始频率。
3. 将梅尔域上每个三角滤波器的起始、中间和截止频率转换到线性频率域，并对DFT之后的谱特征进行滤波，得到 $P$ 个滤波器组的能量，进行对数操作，得到Fbank特征。
4. 在Fbank特征基础上进行倒谱变换（IDFT），得到MFCC特征。

梅尔滤波器组的公式为：

$$H_m(k)=\{\begin{array}{ll}0& \text{if }k<f(m-1)\\ \frac{k-f(m-1)}{f(m)-f(m-1)}& \text{if }f(m-1)\le k<f(m)\\ \frac{f(m+1)-k}{f(m+1)-f(m)}& \text{if }f(m)\le k<f(m+1)\\ 0& \text{if }k>f(m+1)\end{array}$$

其中，$m$ 表示第 $m$ 个滤波器组，$k$ 表示第 $k$ 个频率点，$f(m)$ 表示第 $m$ 个滤波器组的起始频率对应的索引值。

5.倒谱分析

倒谱分析用于将频谱的对数进行逆变换，以提取MFCC特征。具体步骤如下：

1. 计算对数谱。
2. 对对数谱进行离散余弦变换（DCT），得到MFCC特征。

6.动态特征计算

动态特征用于捕捉语音特征的时间变化，包括一阶差分和二阶差分。

• 一阶差分（类比速度）：

  $$\Delta c_t=\frac{c_{t+1}-c_{t-1}}{2}$$

• 二阶差分（类比加速度）：

  $$\Delta \Delta c_t=\frac{\Delta c_{t+1}-\Delta c_{t-1}}{2}$$

7.能量计算

能量用于描述语音信号的强度，最简单的能量计算公式为：

$$E=\sum x[n{]}^2$$

8.特征总结

Fbank特征通常用于深度神经网络（DNN）的训练，它是一种基于滤波器组的声音特征提取方法，常用于语音识别和语音处理领域。

MFCC特征是一种常见的语音特征提取方法，一般包括39维：

• 12维原始MFCC
• 12维一阶差分
• 12维二阶差分
• 1维能量
• 1维能量的一阶差分
• 1维能量的二阶差分

这些特征通常用于对角高斯混合模型（GMM）的训练，因为它们的各维度之间相关性较小，适合用于统计建模和分类任务。

三.课后作业

给定一段音频，请提取12维MFCC特征和23维FBank，阅读代码预加重、分帧、加窗部分，完善作业代码中FBank特征提取和MFCC特征提取部分，并给出最终的FBank特征和MFCC特征，存储在纯文本中，用默认的配置参数，无需进行修改。

import librosa
import numpy as np
from scipy.fftpack import dct
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('Agg')

# 展示频谱图
def plot_spectrogram(spec, note, file_name):
    """绘制频谱图
        :param spec: 特征维度 x 帧数 的数组（实数）
        :param note: 图片标题
        :param file_name: 文件名
    """ 
    fig = plt.figure(figsize=(20, 5))
    heatmap = plt.pcolor(spec)
    fig.colorbar(mappable=heatmap)
    plt.xlabel('time(s)')
    plt.ylabel(note)
    plt.tight_layout()
    plt.savefig(file_name)

# 预加重系数配置
alpha = 0.97

# 分帧配置
frame_len = 400      # 25毫秒, fs=16kHz
frame_shift = 160    # 10毫秒, fs=16kHz
fft_len = 512

# Mel滤波器配置
num_filter = 23
num_mfcc = 12

# 读取wav文件
wav, fs = librosa.load('./test.wav', sr=None)


def preemphasis(signal, coeff=alpha):
    """对输入信号进行预加重处理。

        :param signal: 需要过滤的信号
        :param coeff: 预加重系数，0表示无过滤，默认为0.97
        :returns: 过滤后的信号
    """
    # 对输入信号进行预加重处理
    # 预加重公式：y[n] = x[n] - a * x[n-1]
    # np.append(signal[0], ...) 确保返回的信号长度与输入信号相同
    return np.append(signal[0], signal[1:] - coeff * signal[:-1])


def enframe(signal, frame_len=frame_len, frame_shift=frame_shift, win=np.hamming(frame_len)):
    """使用Hamming窗函数进行分帧。
        :param signal: 待分帧的信号
        :param frame_len: 每帧的长度，默认为400
        :param frame_shift: 帧移长度，默认为160
        :param win: 窗函数，默认为Hamming窗
        :returns: 分帧后的信号，num_frames x frame_len 的数组
    """

    # 获取信号的采样点数
    num_samples = signal.size

    # 计算帧的数量
    # (num_samples - frame_len) // frame_shift 是帧移后的有效帧数
    # +1 是因为第一帧是从0开始的
    num_frames = np.floor((num_samples - frame_len) / frame_shift) + 1

    # 初始化分帧后的数组，大小为 num_frames x frame_len
    frames = np.zeros((int(num_frames), frame_len))

    # 将信号分成若干帧，每帧长度为 frame_len，并加上窗函数
    for i in range(int(num_frames)):
        # 取出当前帧的数据
        frames[i, :] = signal[i * frame_shift:i * frame_shift + frame_len]

        # 乘以窗函数进行加窗
        frames[i, :] = frames[i, :] * win

    return frames


def get_spectrum(frames, fft_len=fft_len):
    """使用FFT获取频谱
        :param frames: 分帧后的信号，num_frames x frame_len 的数组
        :param fft_len: FFT长度，默认为512
        :returns: 频谱，num_frames x (fft_len/2 + 1) 的数组（实数）
    """
    # 对每帧信号进行快速傅里叶变换（FFT）
    # 计算得到的cFFT是一个复数数组，大小为 num_frames x fft_len
    cFFT = np.fft.fft(frames, n=fft_len)
    
    # 获取有效的频谱长度
    # 对于实数输入信号，FFT的频谱是对称的，只需保留前一半加一个元素
    valid_len = int(fft_len / 2) + 1
    
    # 取FFT的绝对值（幅度谱），并只保留前valid_len个元素
    # 结果spectrum是一个实数数组，大小为 num_frames x valid_len
    spectrum = np.abs(cFFT[:, 0:valid_len])
    
    return spectrum


def fbank(spectrum, num_filter=num_filter, fs=fs, fft_len=fft_len):
    """从频谱中获取Mel滤波器组特征
        :param spectrum: num_frames x (fft_len/2 + 1) 的数组（实数）
        :param num_filter: Mel滤波器数量，默认为23
        :param fs: 采样率，默认为16kHz
        :param fft_len: FFT长度，默认为512
        :returns: fbank特征，num_frames x num_filter 的数组 
        不要忘记在Mel滤波后进行对数操作！
    """
    # 计算Mel滤波器组

    # 定义最低频率
    low_freq = 0

    # 定义最高频率（采样率的一半）
    high_freq = fs / 2

    # 将最低频率和最高频率转换为Mel频率
    # Mel频率是将实际频率映射到感知频率的尺度
    mel_low_freq = 2595 * np.log10(1 + low_freq / 700)
    mel_high_freq = 2595 * np.log10(1 + high_freq / 700)

    # 在Mel频率尺度上等间距划分num_filter+2个点
    # 加2是因为包含了起始点和终止点
    mel_points = np.linspace(mel_low_freq, mel_high_freq, num_filter + 2)

    # 将这些点从Mel频率转换回实际频率
    hz_points = 700 * (10**(mel_points / 2595) - 1)

    # 将实际频率转换为对应的FFT bin（频率点对应的索引）
    # FFT的频率范围是从0到fs/2
    bin_points = np.floor((fft_len + 1) * hz_points / fs).astype(int)

    # 创建滤波器组矩阵
    # 这里的fbank是一个num_filter行，(fft_len/2 + 1)列的矩阵
    # 每一行对应一个Mel滤波器
    fbank = np.zeros((num_filter, int(np.floor(fft_len / 2 + 1))))

    # 为每一个Mel滤波器生成三角形滤波器
    for i in range(1, num_filter + 1):
        left = bin_points[i - 1]    # 三角形滤波器的左边界
        center = bin_points[i]      # 三角形滤波器的中心
        right = bin_points[i + 1]   # 三角形滤波器的右边界
        
        # 填充三角形滤波器的左半部分
        for j in range(left, center):
            fbank[i - 1, j] = (j - bin_points[i - 1]) / (bin_points[i] - bin_points[i - 1])
        
        # 填充三角形滤波器的右半部分
        for j in range(center, right):
            fbank[i - 1, j] = (bin_points[i + 1] - j) / (bin_points[i + 1] - bin_points[i])

    # 应用滤波器组到频谱上，并计算滤波后的能量
    # 通过矩阵乘法将频谱特征与滤波器组相乘
    feats = np.dot(spectrum, fbank.T)

    # 避免log(0)的情况，将所有为0的值替换为最小正浮点数值
    feats = np.where(feats == 0, np.finfo(float).eps, feats)

    # 对滤波后的能量取对数
    feats = np.log(feats)

    return feats


def mfcc(fbank_feats, num_mfcc=num_mfcc):
    """从fbank特征中获取MFCC特征

        :param fbank_feats: num_frames x num_filter 的数组（实数）
        :param num_mfcc: MFCC系数数量，默认为12
        :returns: MFCC特征，num_frames x num_mfcc 的数组 
    """
    # 对fbank特征进行DCT变换
    feats = dct(fbank_feats, type=2, axis=1, norm='ortho')[:, :num_mfcc]

    # 让MFCC特征更加稳健
    feats -= (np.mean(feats, axis=0) + 1e-8)

    return feats

def write_file(feats, file_name):
    """将特征写入文件
        :param feats: num_frames x feature_dim 的数组（实数）
        :param file_name: 文件名
    """
    f = open(file_name, 'w')
    (row, col) = feats.shape
    for i in range(row):
        f.write('[')
        for j in range(col):
            f.write(str(feats[i, j]) + ' ')
        f.write(']\n')
    f.close()


def main():
    # 加载音频文件
    # librosa.load()函数将音频文件加载为时域信号，并返回音频时间序列和采样率
    wav, fs = librosa.load('./test.wav', sr=None)

    # 对音频信号进行预加重处理
    # preemphasis()函数对信号进行预加重，强调高频部分
    signal = preemphasis(wav)

    # 对预处理后的信号进行分帧处理
    # enframe()函数将信号分割成多个帧，每帧长度为frame_len，并加上Hamming窗
    frames = enframe(signal)

    # 获取每帧的频谱
    # get_spectrum()函数对每一帧进行FFT，获取频谱
    spectrum = get_spectrum(frames)

    # 计算FBank特征
    # fbank()函数从频谱中提取Mel滤波器组特征
    fbank_feats = fbank(spectrum)
    print(fbank_feats.shape) # (356, 23)  
    # 计算MFCC特征
    # mfcc()函数从FBank特征中提取MFCC特征
    mfcc_feats = mfcc(fbank_feats)
    print(mfcc_feats.shape) # (356, 12) #356 表示帧数，12 表示每帧提取的 MFCC 系数数量

    # 绘制FBank特征的频谱图，并保存为fbank.png
    # plot_spectrogram()函数绘制频谱图并保存到文件
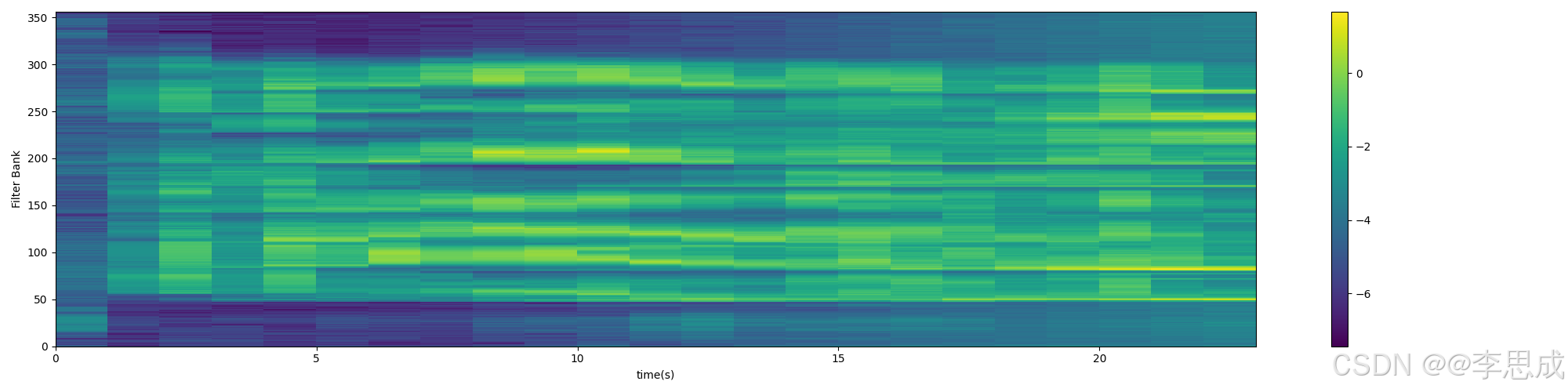
    plot_spectrogram(fbank_feats, 'Filter Bank', 'fbank.png')

    # 将FBank特征写入文件test.fbank
    # write_file()函数将特征数组写入文本文件
    write_file(fbank_feats, './test.fbank')

    # 绘制MFCC特征的频谱图，并保存为mfcc.png
    # 注意：由于MFCC特征的维度较高，转置后绘制频谱图
    plot_spectrogram(mfcc_feats.T, 'MFCC', 'mfcc.png')

    # 将MFCC特征写入文件test.mfcc
    write_file(mfcc_feats, './test.mfcc')


if __name__ == '__main__':
    main()

FBank特征的频谱图:

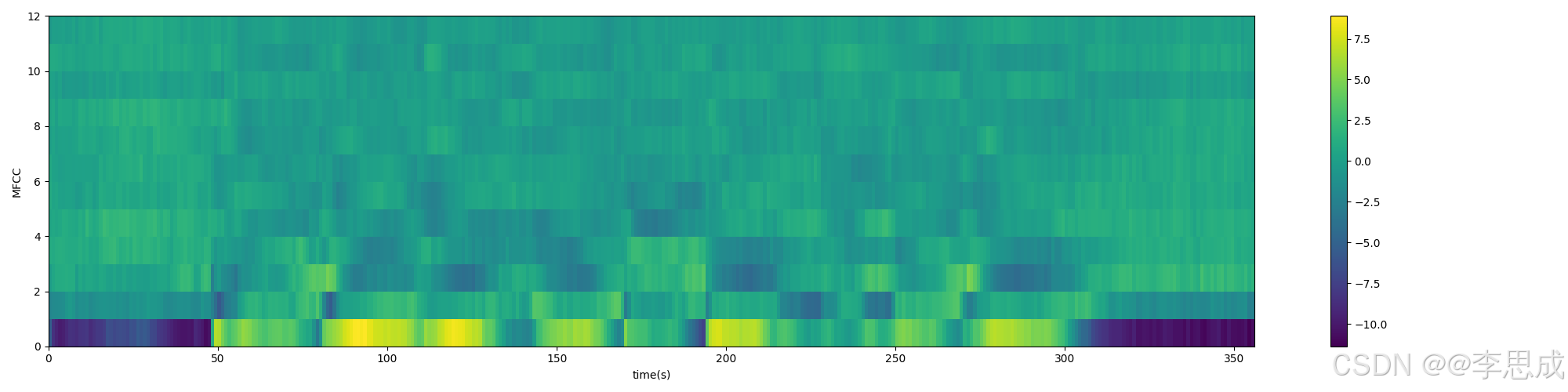
MFCC特征的频谱图: