1.求函數極值
定义:
设函数
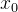
如果对于该邻域内异于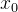
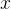


那么就称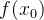

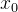
极大值与极小值统称为极值,极大值点与极小值点统称为极值点 。
例题1:
求函数
对
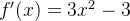
令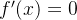
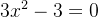

当
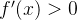
当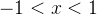
当
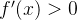
所以
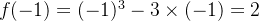

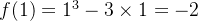
例题2:
求函数
求导得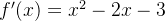
令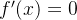
,解得


当
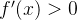
当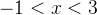
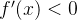
当
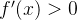
则极大值为,
极小值为。
例题3:
求函数
求导,根据乘积求导法则,
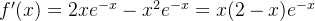
令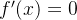

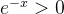


当
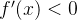
当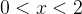
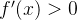
当
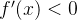
所以极小值为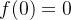
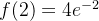
例题4:
求函数
设函数
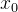
如果对于该邻域内异于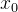
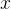


那么就称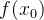

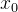
极大值与极小值统称为极值,极大值点与极小值点统称为极值点 。
求函数
对
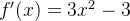
令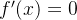
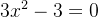

当
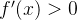
当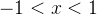
当
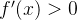
所以
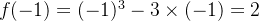

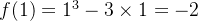
求函数
求导得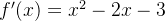
令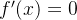
,解得


当
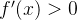
当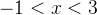
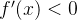
当
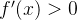
则极大值为,
极小值为。
求函数
求导,根据乘积求导法则,
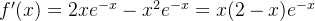
令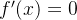

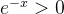


当
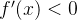
当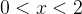
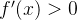
当
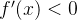
所以极小值为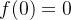
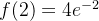
求函数
道可道,非常道;名可名,非常名。 无名,天地之始,有名,万物之母。 故常无欲,以观其妙,常有欲,以观其徼。 此两者,同出而异名,同谓之玄,玄之又玄,众妙之门。