第1章 實分析與函數論:快速回顧(上)
一、集合相關例題
例題1:集合運算
已知集合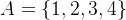
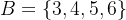
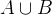
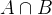
(假設全集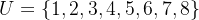
解析:
- 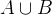
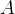
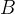

- 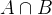
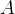
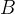

- 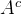
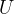
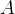

例題2:子集關係判斷
判斷集合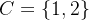
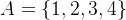
解析:
- 對於集合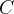
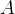

- 又因為集合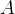
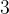
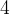


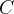
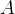
例題3:等價關係驗證
在整數集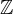
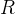
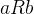
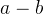
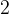
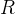
解析:
- 自反性:對於任意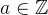
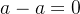
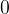
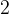
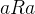
- 對稱性:若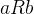
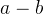
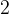

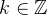
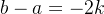
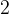
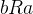
- 傳遞性:若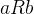
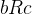

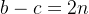
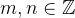
,能被
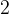
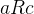
所以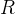
例題4:商集的構造
對於例題3中的等價關係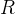

解析:
- 等價類![[0]_R=\{a\in\mathbb{Z}:a - 0](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIwJTVEX1IlM0QlNUMlN0JhJTVDaW4lNUNtYXRoYmIlN0JaJTdEJTNBYSUyMC0lMjAw)
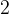
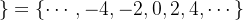
- 等價類![[1]_R=\{a\in\mathbb{Z}:a - 1](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIxJTVEX1IlM0QlNUMlN0JhJTVDaW4lNUNtYXRoYmIlN0JaJTdEJTNBYSUyMC0lMjAx)
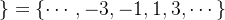
所以![\mathbb{Z}/R=\{[0]_R,[1]_R\}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNtYXRoYmIlN0JaJTdE/R%3D%5C%7B%5B0%5D_R%2C%5B1%5D_R%5C%7D)
例題5:集合包含關係證明
證明若


解析:
任取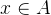

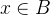
又因為
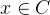
即對於任意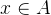
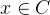

例題6:集合運算性質證明
證明
解析:
- 先證
任取
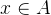

若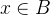

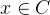

所以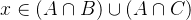

- 再證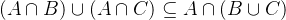
任取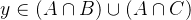
若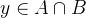
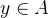
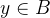
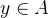


若

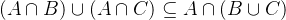
综上,
例題7:利用集合運算求集合
已知


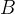
解析:
根據集合運算的性質,
先求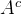



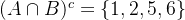
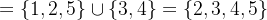
例題8:無限集合的子集關係
設

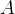
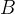
解析:
對於集合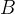
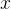


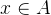

又因為存在0 < x<1的實數,比如




二、映射相關例題
例題1:映射的判斷
判斷
