【leetcode】排列序列

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

"123"
"132"
"213"
"231"
"312"
"321"

给定 n 和 k，返回第 k 个排列。

示例 1：

输入：n = 3, k = 3
输出："213"

示例 2：

输入：n = 4, k = 9
输出："2314"

示例 3：

输入：n = 3, k = 1
输出："123"

提示：

1 <= n <= 9
1 <= k <= n!

解题思路：

例如： n = 4， k = 9

可以知道全排列有：4*3*2*1 = 24种，如下：红色框住的为第9个

从上图可知，以1开头的全排列 (4-1)! = 6 共6种；

9 / 6 = 1······3，也就是该数位于2开头的第三个。

同理，第一位2确定后，剩下三位 1 3 4，接下来需要确定第二位；

由上面的图片可知， 1 3 4全排列每一列分别有两个数（3-1）！，3 / 2 = 1······1，可知位于第二列开头的第一个

然后确定第三位，第三位则还剩下2个数：1和4；

1和4的全排列：

1 4排列，每类（2-1)! = 1，1 / 1 = 1·····0,可知位于1开头的第一个

最后一位数，只有一种情况: （1-1)！ = 1

具体算法如下：

1、定义一个逆康托数组，记录n位数字对应每个数字开头序列的个数，例如4位数prenum[1, 1, 2, 6]

将k值-1，再进行计算，这里-1是为了 9 % 6 = 3，而数组下标从0开始，-1后方便计算。

2、定义一个valid数组[0.....n];记录还没有被使用的数字，已经使用的需要移除

3、(k -1 ) / prenum[n - i - 1] + 1就是分别计算每一位数字位于那一列；例如（9 -1）/ 6 + 1= 2，说明第一个数字为2，ans累加vali[2] ,2被使用后erase掉，valid中剩余[0,1,3,4]

然后k记录剩余未计算的数 8 % 6 = 2

k = 2再重复计算，可得到 2/2 + 1 = 2; 再取走valid中的第2个

同理依次取完。

完整代码如下：

class Solution {
public:
    string getPermutation(int n, int k) {
        //prenum = {0!, 1!, 2!, 3!, .....(n-1)!}
        vector<int> pernum(n);
        pernum[0] = 1;
        for(int i= 1; i < n; i++) {
            pernum[i] = pernum[i-1] * i;
        }

        //k-- 方便取余后计算
        k--;
        string ans;
        vector<int> valid(n+1);
        //生成[0,1,2....n]的数组
        iota(valid.begin(), valid.end(), 0);
        for(int i = 0; i < n; i++) {
            int order = k / pernum[n-i-1] + 1;
            ans += (valid[order] + '0');
            //用了就从数组中删除
            valid.erase(valid.begin() + order);
            k %= pernum[n-i-1];
        }
        return ans;

    }
};

拓展：康托展开，也就是在全排列中，给定一个序列，求该序列位于第几个。

#include <iostream>
#include <string>
using namespace std;

class Solution {

public:
    //求阶乘
    int fact(int x) {
        int ret = 1;
        for(int i = 2; i <= x; i++) {
            ret *= i;
        }
        return ret;
    }

    int getStringId(string str) {
        int len = str.size();
        int ans = 0;
        for(int i = 0; i < len; i++) {
            int cnt = 0;
            //记录后面的数有几个比当前的数小；
            //例如2314  314中只有1个数比第一位小，说明该数位于第二列。
            for(int j = i + 1 ; j < len; j++) {
                if(str[j] < str[i]) {
                    cnt ++;
                }
            }
            ans += cnt*fact(len- i -1);
        }
        return ans+1;
    }
};
int main()
{
    string s;
    cin >> s;
    Solution sol;
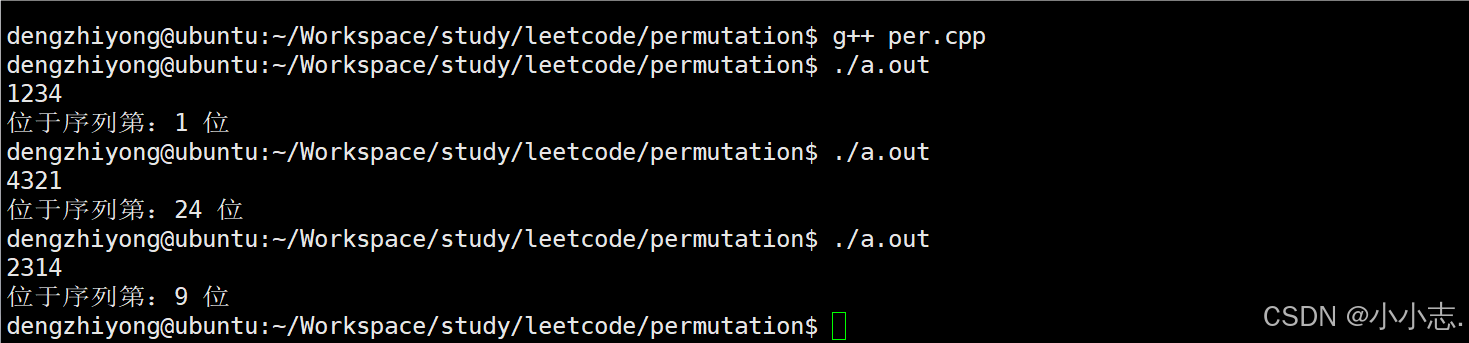
    cout << "位于序列第：" << sol.getStringId(s) << " 位" << endl;
    return 0;
}

【leetcode】排列序列

悦读