在看MIT的线性代数课,感谢Gilbert Strang教授,让我对线性代数有了新的理解。本篇从对应的课程视频和课本出发,讲一讲有意思的AX=b的2种解释和矩阵乘法的5种视角,当然,这属于我的个人阐发,以保留思维的启迪。
AX=b的2种解释
我就随便举例子,比如矩阵A和矩阵B
A
=
[
1
2
3
4
]
B
=
[
6
2
1
4
4
1
7
6
1
]
A= \begin{bmatrix}1 &2 \\ 3&4 \end{bmatrix} \ \ \ \ \ \ B= \begin{bmatrix}6 &2 & 1\\ 4&4 &1 \\ 7 & 6 &1 \end{bmatrix}
A=[1324] B=⎣
⎡647246111⎦
⎤
如果我们将其写做方程的形式,不如假设矩阵A对应方程的右值为5和6,那么就有
x
1
+
2
x
2
=
5
3
x
1
+
4
x
2
=
6
x_1 + 2x_2 = 5 \\ 3x_1 + 4x_2 =6
x1+2x2=53x1+4x2=6
Row Picture
借助初高中所学知识,我们知道 这其实是
x
1
x
2
x_1x_2
x1x2平面中的两条直线,在平面中两条直线应该只有相交和平行两种情况 。我们可以借助matlab画出这两条直线:
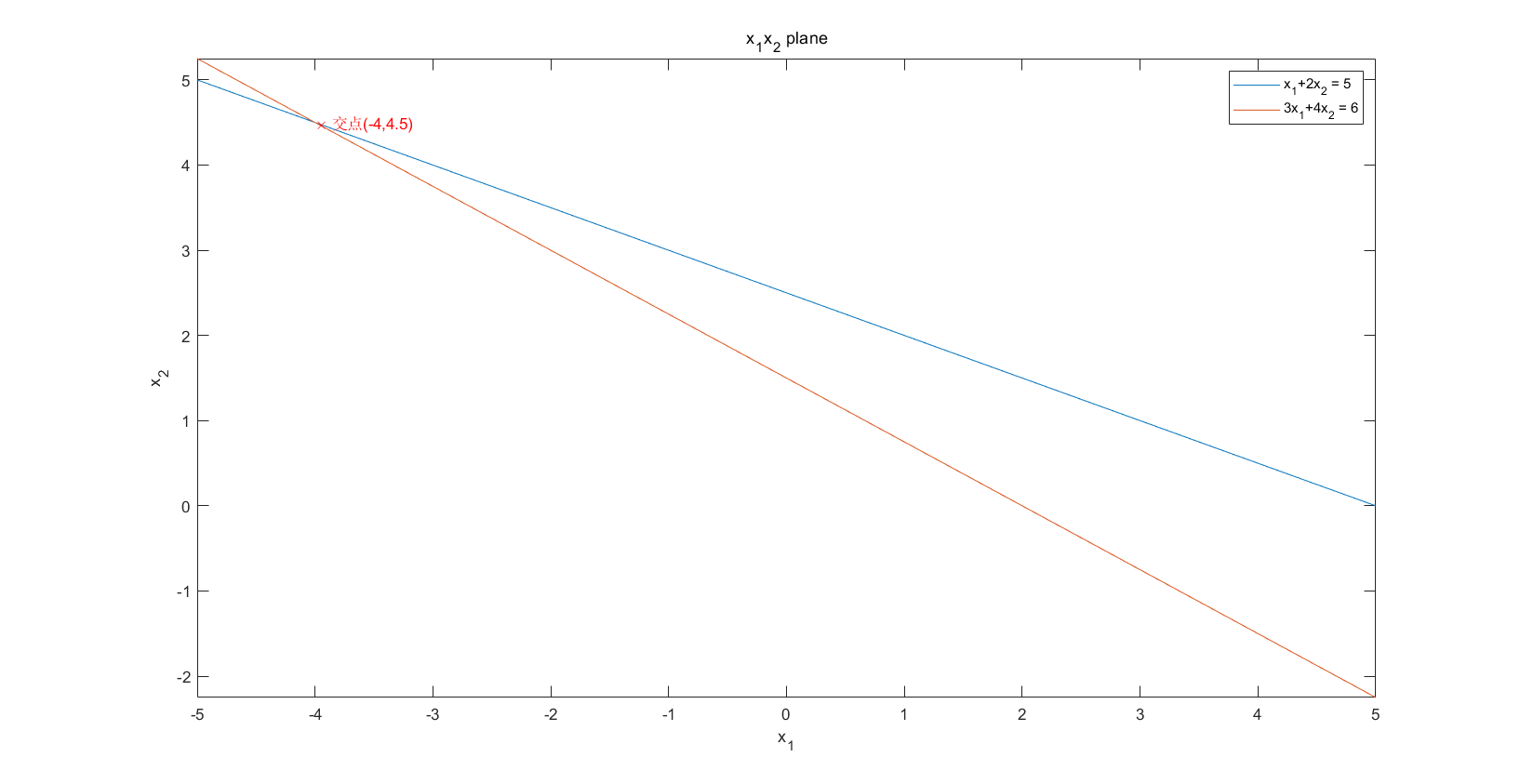
对应的绘图代码为:
% 画二维直线
% 定义
syms x1;
y1 = 2.5-0.5*x1; y2 = 1.5-3/4*x1;
% fplot画线
fplot(y1); hold on; fplot(y2);
% 直线标注
legend('x_1+2x_2 = 5','3x_1+4x_2 = 6');
% solve求解交点
xp = double(solve(y1==y2)); % 转换数据格式
yp = 2.5-0.5*xp;
% 交点标注
text(xp,yp,['\times ','交点','(',num2str(xp),',',num2str(yp),')'],Color = 'red');
% 标题和坐标轴
title('x_1x_2 plane');
xlabel('x_1');
ylabel('x_2');
我们可以发现两条直线有一个交点,这个交点是(-4,4.5)。实际上这个交点也就是原方程的解。应该说明:这种解空间中的交点情况与矩阵方程的对应关系,就是“Row Picture”,即将矩阵所表示的方程视作空间中的点、线、面。我将其理解为可视化的解空间。
我们再来看复杂点的三维场景,假设矩阵B对应方程的右值为8、9和10,即
6
x
1
+
2
x
2
+
x
3
=
8
4
x
1
+
4
x
2
+
x
3
=
9
7
x
1
+
6
x
2
+
x
3
=
10
6x_1 +2x_2 + x_3= 8 \\ 4x_1 + 4x_2 + x_3=9 \\ 7x_1 + 6x_2 + x_3=10
6x1+2x2+x3=84x1+4x2+x3=97x1+6x2+x3=10
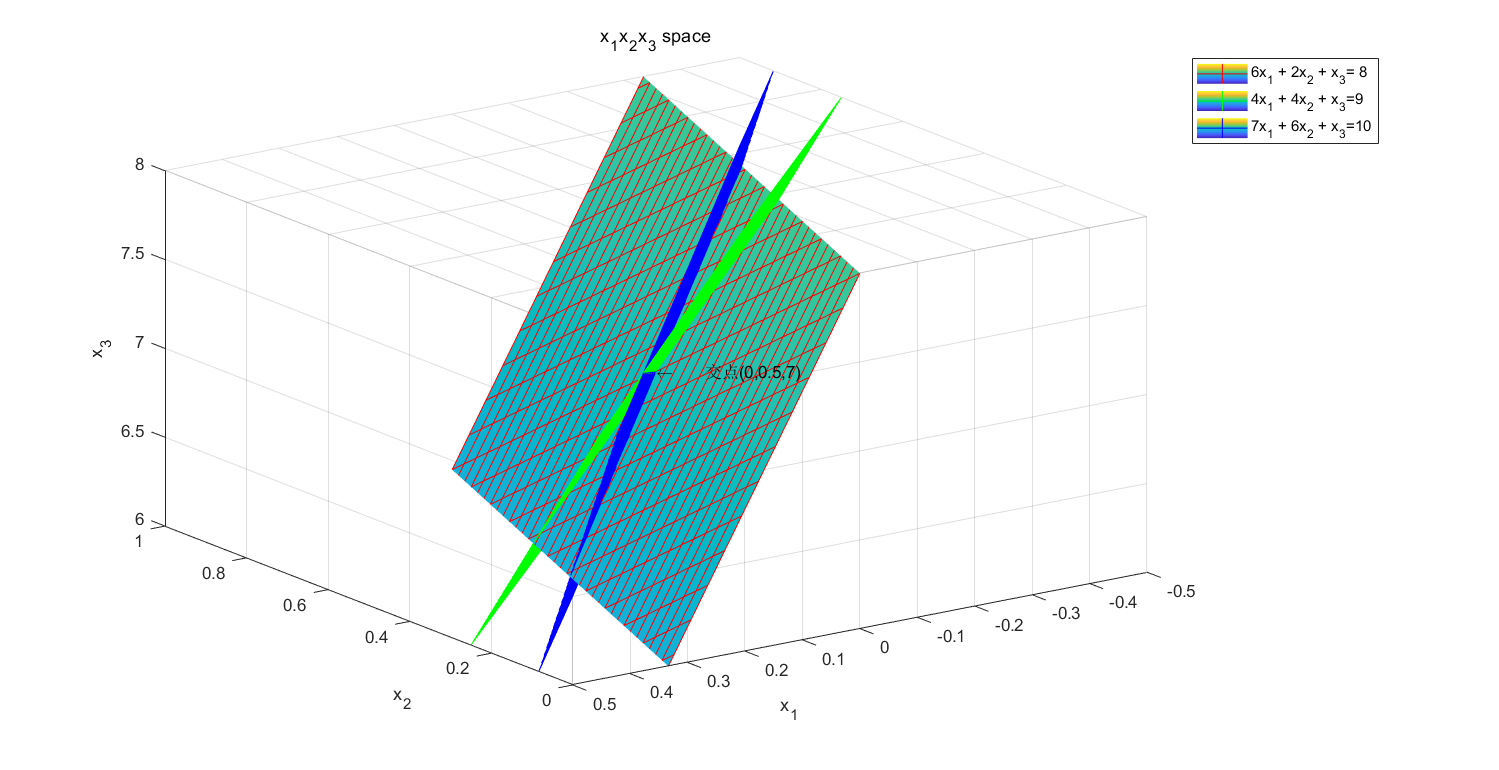
对应的绘图结果和绘图代码分别为:
% 画三维平面
% 定义
syms x1;
syms x2;
y1 = 8-6*x1-2*x2; y2 = 9-4*x1-4*x2; y3 = 10-7*x1-6*x2;
% fmesh画平面
fsurf(y1,EdgeColor='r'); hold on; fsurf(y2,EdgeColor='g'); hold on ;fsurf(y3,EdgeColor='b');
% 平面标注
legend('6x_1 + 2x_2 + x_3= 8','4x_1 + 4x_2 + x_3=9','7x_1 + 6x_2 + x_3=10');
% solve求解交点
result = solve([y1==y2,y1==y3]);
xp = double(result.x1); % 转换数据格式
yp = double(result.x2);
zp = 8-6*xp-2*yp;
% 交点标注
text(xp,yp,zp,['\leftarrow ',' 交点','(',num2str(xp),',',num2str(yp),',',num2str(zp),')'],Color = 'black');
% 标题和坐标轴
title('x_1x_2x_3 space');
xlabel('x_1'); xlim([-0.5,0.5]);
ylabel('x_2'); ylim([0,1]);
zlabel('x_3'); zlim([6,8]);
同样我们可以发现三个平面有三条交线,取其中某条交线与第三个平面的交点就是(0,0.5,7),同样可以验证这个交点也就是原方程的解。借助Matlab的绘图工具,我们弥补了手绘这种解空间时不够直观的缺陷。可以想象,对于更高维的空间,矩阵所表示的方程仍旧是空间中的点、线和超平面。
Column Picture
“Column Picture” 蕴含了我们将矩阵视作线性代数运算的根本性质,即将其应视作两种基本运算的组合,即加法运算和标量乘法运算,也即 a x ⃗ + b y ⃗ a\vec{x}+b\vec{y} ax+by 的形式。我将其理解为矩阵列的加权和 。
我们来看一个阐述就能明白,以矩阵A对应的方程为例:
[
1
2
3
4
]
[
x
1
x
2
]
=
[
5
6
]
\begin{bmatrix}1 &2 \\ 3&4 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix}5 \\ 6 \end{bmatrix}
[1324][x1x2]=[56]
实际上,
x
1
x_1
x1和
x
2
x_2
x2就是对矩阵A中两列所分配的加权系数,即上式应该可以写成:
x
1
[
1
3
]
+
x
2
[
2
4
]
=
[
5
6
]
x_1 \begin{bmatrix}1 \\ 3 \end{bmatrix} + x_2 \begin{bmatrix}2 \\ 4 \end{bmatrix} = \begin{bmatrix}5 \\ 6 \end{bmatrix}
x1[13]+x2[24]=[56]
Gilbert Strang教授希望我们在这里能着重体会,去真正明白线性代数运算中所谓的线性。其实,观察这个解的结构,我们就很容易想到,如果b作为结果列,其必然是矩阵A两列的线性组合,也就是说,所谓方程的解,即应该是一组满足了b列的矩阵列加权和系数。体会到这一层,比直接上来告诉你去按照 矩阵点乘的运算法则 将
A
X
=
b
AX=b
AX=b展开为方程,再利用消元法去求解方程要好得多,因为你发现了线性的含义所在。
实际上,还有其他方式同样可以说明线性。在这里,我们发现X作为列矩阵是放在了矩阵A的右边,从而实现的是对矩阵A的列操作。如果对于一般的矩阵乘法,放在右边的某列系数会是怎样的呢?我们下面就回答这个问题。
矩阵乘法的5种视角
我们面对的问题即求解矩阵乘法:
A
B
?
AB \ \ ?
AB ?
第一视角:点乘法则
给出A和B的例子:
A
1
=
[
1
3
2
4
]
B
1
=
[
5
7
6
8
]
A_1= \begin{bmatrix}1 &3 \\ 2&4 \end{bmatrix} \ \ \ \ \ \ B_1= \begin{bmatrix}5 &7 \\ 6&8 \end{bmatrix}
A1=[1234] B1=[5678]
点乘法则广泛应用,但其实一开始并不能直观指出,即左矩阵的第i行的元素与右矩阵第j列元素的点乘作为结果矩阵第i行第j列的元素。结合例子,此种思路可表述为:
A
1
B
1
=
[
1
3
2
4
]
[
5
7
6
8
]
=
[
1
×
5
+
3
×
6
1
×
7
+
3
×
8
2
×
5
+
4
×
6
2
×
7
+
4
×
8
]
=
[
23
31
34
46
]
A_1B_1 = \begin{bmatrix}1 &3 \\ 2&4 \end{bmatrix} \begin{bmatrix}5 &7 \\ 6&8 \end{bmatrix} = \begin{bmatrix}1\times5+3\times6 &1\times7+3\times8 \\ 2\times5+4\times6 & 2\times7+4\times8 \end{bmatrix} = \begin{bmatrix}23 &31 \\ 34&46 \end{bmatrix}
A1B1=[1234][5678]=[1×5+3×62×5+4×61×7+3×82×7+4×8]=[23343146]
第二视角:行的线性组合
我们在这里回答“放在右边的某列系数会是怎样的呢?”这个问题,答案为对行的线性组合。即此时将B作为一个整体看待,而将A的各行系数视为对B中行的加权。
修改A和B的例子:
A
2
=
[
1
3
2
4
]
B
2
=
[
5
7
6
8
]
A_2= \begin{bmatrix}1 \\ 3 \\ 2 \\ 4 \end{bmatrix} \ \ \ \ \ \ B_2= \begin{bmatrix}5 &7 & 6&8 \end{bmatrix}
A2=⎣
⎡1324⎦
⎤ B2=[5768]
此种思路就表述为:
A
2
B
2
=
[
1
3
2
4
]
[
5
7
6
8
]
=
[
1
×
(
5
7
6
8
)
3
×
(
5
7
6
8
)
2
×
(
5
7
6
8
)
4
×
(
5
7
6
8
)
]
=
[
5
7
6
8
15
21
18
24
10
14
12
16
20
28
24
32
]
A_2 B_2= \begin{bmatrix}1 \\ 3 \\ 2 \\ 4 \end{bmatrix} \begin{bmatrix}5 &7 & 6&8 \end{bmatrix} = \begin{bmatrix}1 \times (5 &7 & 6&8) \\ 3 \times (5 &7 & 6&8) \\ 2 \times (5 &7 & 6&8) \\ 4 \times (5 &7 & 6&8) \end{bmatrix} = \begin{bmatrix}5 &7 & 6&8 \\ 15&21 & 18&24 \\ 10 &14 & 12&16\\ 20 & 28 & 24&32 \end{bmatrix}
A2B2=⎣
⎡1324⎦
⎤[5768]=⎣
⎡1×(53×(52×(54×(5777766668)8)8)8)⎦
⎤=⎣
⎡5151020721142861812248241632⎦
⎤
第三视角:列的线性组合
其实在
A
X
=
b
AX=b
AX=b的讨论中,我们已经知道了“放在左边的某列系数会是怎样的呢?”的答案,其应该就是关于列的线性组合。 修改A和B的例子为:
A
3
=
[
1
3
2
4
]
B
3
=
[
5
7
6
8
]
A_3= \begin{bmatrix}1 &3 & 2 & 4 \end{bmatrix} \ \ \ \ \ \ B_3= \begin{bmatrix}5 \\ 7 \\ 6\\8 \end{bmatrix}
A3=[1324] B3=⎣
⎡5768⎦
⎤
此种思路表述为:
A
3
B
3
=
[
1
3
2
4
]
[
5
7
6
8
]
=
5
×
1
+
7
×
3
+
6
×
2
+
8
×
4
=
70
A_3B_3= \begin{bmatrix}1 &3 & 2 & 4 \end{bmatrix} \begin{bmatrix}5 \\ 7 \\ 6\\8 \end{bmatrix} =5\times 1+7\times 3+ 6 \times2 + 8 \times 4 = 70
A3B3=[1324]⎣
⎡5768⎦
⎤=5×1+7×3+6×2+8×4=70
这是一个足够特殊的例子,容易发现,此时按照前三种视角得到的方程式都将得到这样一致的一个求和式,但它们得到这个求和式的角度不同的。综合第二视角和第三视角,我们可以自然地发现左乘的矩阵是对矩阵行的线性组合,而右乘的矩阵是对矩阵列的线性组合。
第四视角:列行向量的线性组合
下面我们重新看待 A 1 B 1 A_1B_1 A1B1 ,基于前面的理解,实际上矩阵乘法也可表述为一种向量乘法的线性组合形式,即:
A
B
=
Σ
(
c
o
l
u
m
n
i
o
f
A
)
×
(
r
o
w
i
o
f
B
)
AB = \Sigma (column_i \ of \ A) × (row_i \ of \ B)
AB=Σ(columni of A)×(rowi of B)
即
A
1
B
1
A_1B_1
A1B1可以重新写为:
A
1
B
1
=
[
1
3
2
4
]
[
5
7
6
8
]
=
[
1
2
]
[
5
7
]
+
+
[
3
4
]
[
6
8
]
=
[
5
7
10
14
]
+
[
18
24
24
32
]
=
[
23
31
34
46
]
A_1B_1= \begin{bmatrix}1 &3 \\ 2&4 \end{bmatrix} \begin{bmatrix}5 &7 \\ 6&8 \end{bmatrix} = \begin{bmatrix}1 \\ 2 \end{bmatrix} \begin{bmatrix}5 &7 \end{bmatrix}+ + \begin{bmatrix}3 \\4 \end{bmatrix} \begin{bmatrix}6 &8 \end{bmatrix} = \begin{bmatrix}5 &7 \\ 10&14 \end{bmatrix} +\begin{bmatrix}18 &24 \\ 24&32 \end{bmatrix} = \begin{bmatrix}23 &31 \\ 34&46 \end{bmatrix}
A1B1=[1234][5678]=[12][57]++[34][68]=[510714]+[18242432]=[23343146]
从这个角度看,我们对于标量乘法和加法何以作为线性空间中的两种基本运算又得到一种直观的感觉。
第五视角:矩阵分块
比如需要我们求解下面这样一个矩阵乘法问题:
A
4
=
[
1
3
0
0
2
4
0
0
0
0
1
0
0
0
0
1
]
B
4
=
[
5
7
0
0
6
8
0
0
0
0
1
0
0
0
0
1
]
A_4= \begin{bmatrix}1 &3 & 0 & 0\\ 2&4 & 0 & 0\\ 0& 0 &1 & 0 \\ 0& 0 & 0 &1 \end{bmatrix} \ \ \ \ \ \ B_4= \begin{bmatrix}5 &7 & 0 & 0\\ 6&8 & 0 & 0\\ 0& 0 &1 & 0 \\ 0& 0 & 0 &1 \end{bmatrix}
A4=⎣
⎡1200340000100001⎦
⎤ B4=⎣
⎡5600780000100001⎦
⎤
尽管借助视角一和视角四都可以求解好这个问题,但其实我们可以站在一个更高的视角看,即
A
4
=
[
A
1
0
0
I
]
B
4
=
[
B
1
0
0
I
]
A_4= \begin{bmatrix}A_1& 0 \\ 0&I \end{bmatrix} \ \ \ \ \ \ B_4= \begin{bmatrix}B_1 &0 \\ 0&I \end{bmatrix}
A4=[A100I] B4=[B100I]
也就是说,矩阵分块后,可将分块的矩阵就视作参与矩阵乘法的一个元素。我们直接按第一视角展开求解,就有
A
4
B
4
=
[
A
1
0
0
I
]
[
B
1
0
0
I
]
=
[
A
1
B
1
+
0
×
0
A
1
×
0
+
0
×
0
×
B
1
+
I
×
0
0
×
0
+
I
×
I
]
=
[
A
1
B
1
0
0
I
]
=
[
23
31
0
0
34
46
0
0
0
0
1
0
0
0
0
1
]
A_4 B_4= \begin{bmatrix}A_1& 0 \\ 0&I \end{bmatrix} \begin{bmatrix}B_1 &0 \\ 0&I \end{bmatrix} = \begin{bmatrix}A_1B_1+ 0 \times 0 &A_1\times0+0\times \\ 0\times B_1+I\times0& 0\times 0+I\times I \end{bmatrix} = \begin{bmatrix}A_1B_1 &0 \\ 0&I \end{bmatrix} = \begin{bmatrix}23 &31 & 0 & 0\\ 34&46 & 0 & 0\\ 0& 0 &1 & 0 \\ 0& 0 & 0 &1 \end{bmatrix}
A4B4=[A100I][B100I]=[A1B1+0×00×B1+I×0A1×0+0×0×0+I×I]=[A1B100I]=⎣
⎡23340031460000100001⎦
⎤
应用之前所求的结果,可以发现运算得到了明显的简化。
上述四个矩阵乘法的Matlab求解过程验证如下:
>> A1 = [1,3;2,4]; B1 = [5,7;6,8];
>> A1*B1
ans =
23 31
34 46
>> A2 = reshape(A1,[4,1]);B2 = reshape(B1,[1,4]);%reshape函数改变矩阵维度
>> A2*B2
ans =
5 6 7 8
10 12 14 16
15 18 21 24
20 24 28 32
>> A3 = reshape(A1,[1,4]);B3 = reshape(B1,[4,1]);
>> A3*B3
ans =
70
>> A4 = [1,3,0,0;2,4,0,0;0,0,1,0;0,0,0,1]; B4 = [5,7,0,0;6,8,0,0;0,0,1,0;0,0,0,1];
>> A4*B4
ans =
23 31 0 0
34 46 0 0
0 0 1 0
0 0 0 1