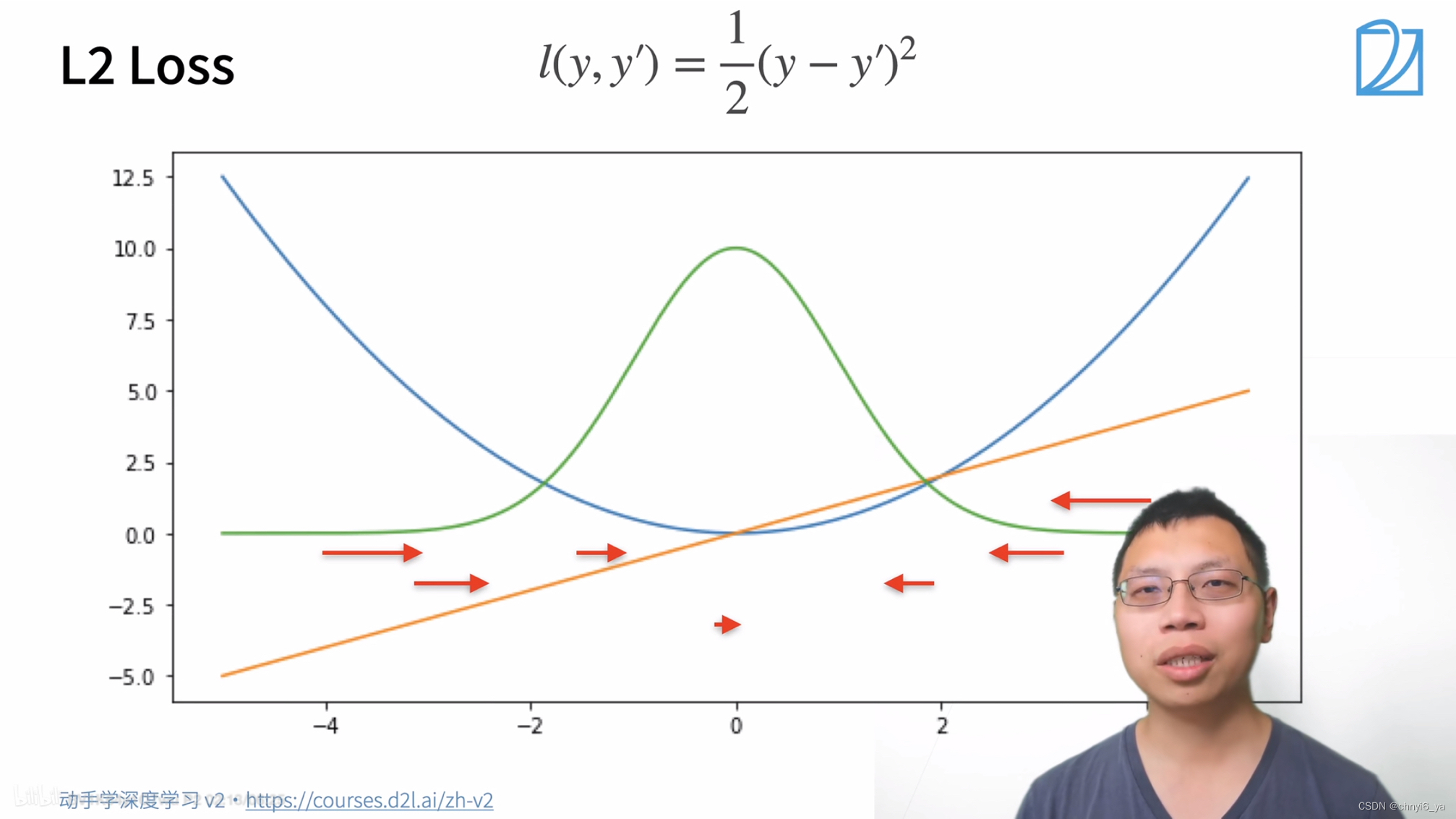
1. L2 loss (均方损失)
除以2就是可以在求导时2和1/2可以相乘抵消。
蓝色的曲线表示:y=0时,变化预测值y’的函数。
绿色曲线表示:似然函数。e^-l。 是一个高斯分布。
橙色的线:表示损失函数的梯度
可以看到:但真实值y‘和真实值隔得比较远的时候,梯度的绝对值比较大,对参数的更新是比较多的。随着预测值慢慢靠近真实值的时候,靠近原点的时候,梯度的绝对值会变得越来越小,也意味着参数更新的幅度也变得越来越小。
但是有时候这够好,比如有时候,我希望离原点远的时候也不要那么大的梯度来更新参数。
似然函数
似然:描述的是在结果已知的情况下,该事件在不同条件下发生的可能性。
似然函数的值越大,表示该事件在对应条件下发生的可能性越大。
- 已知结果就是–模型的参数和样本的参数最接近。其中,模型的参数就是似然函数的变量。
- 上图中,是指y(真实值)取0,来看三个函数曲线随着y‘的变化而变化。
- 看绿色曲线的变化,可以看出,当模型的参数(不同条件)改变使y’左右移动取不同的值时,似然函数的值也在变化,似然函数的值就是事件(模型的参数和样本的参数最接近)发生的可能性。
- 从上图可知,在y=0的时候,当某个参数使得y‘ 能取值为0,那么这个参数是最有可能(似然值)接近样本参数的,也就是可能性最大。
最大似然估计就是要找到使得概率最大的时候的参数值。
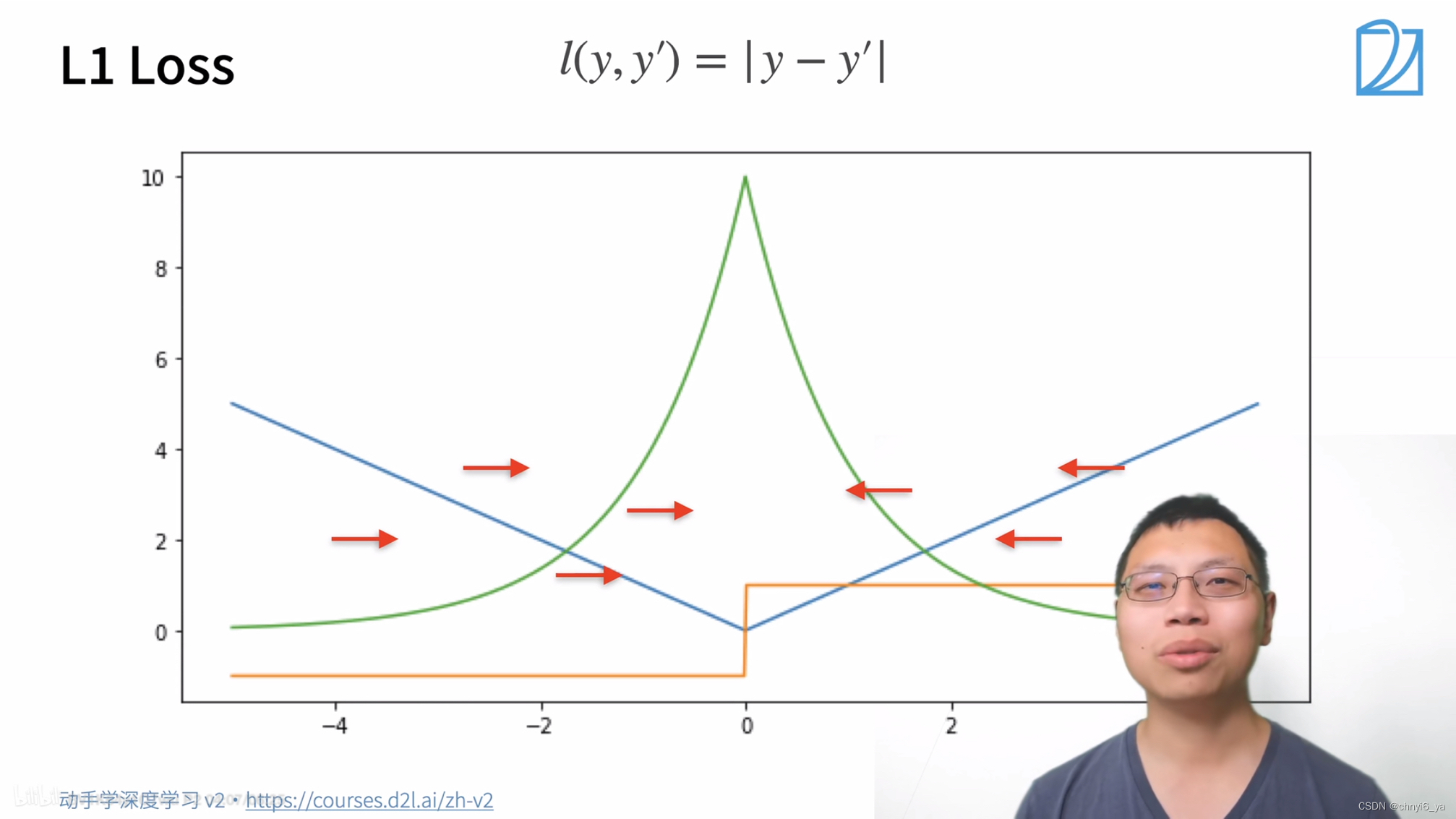
2. L1 Loss(绝对值损失函数)
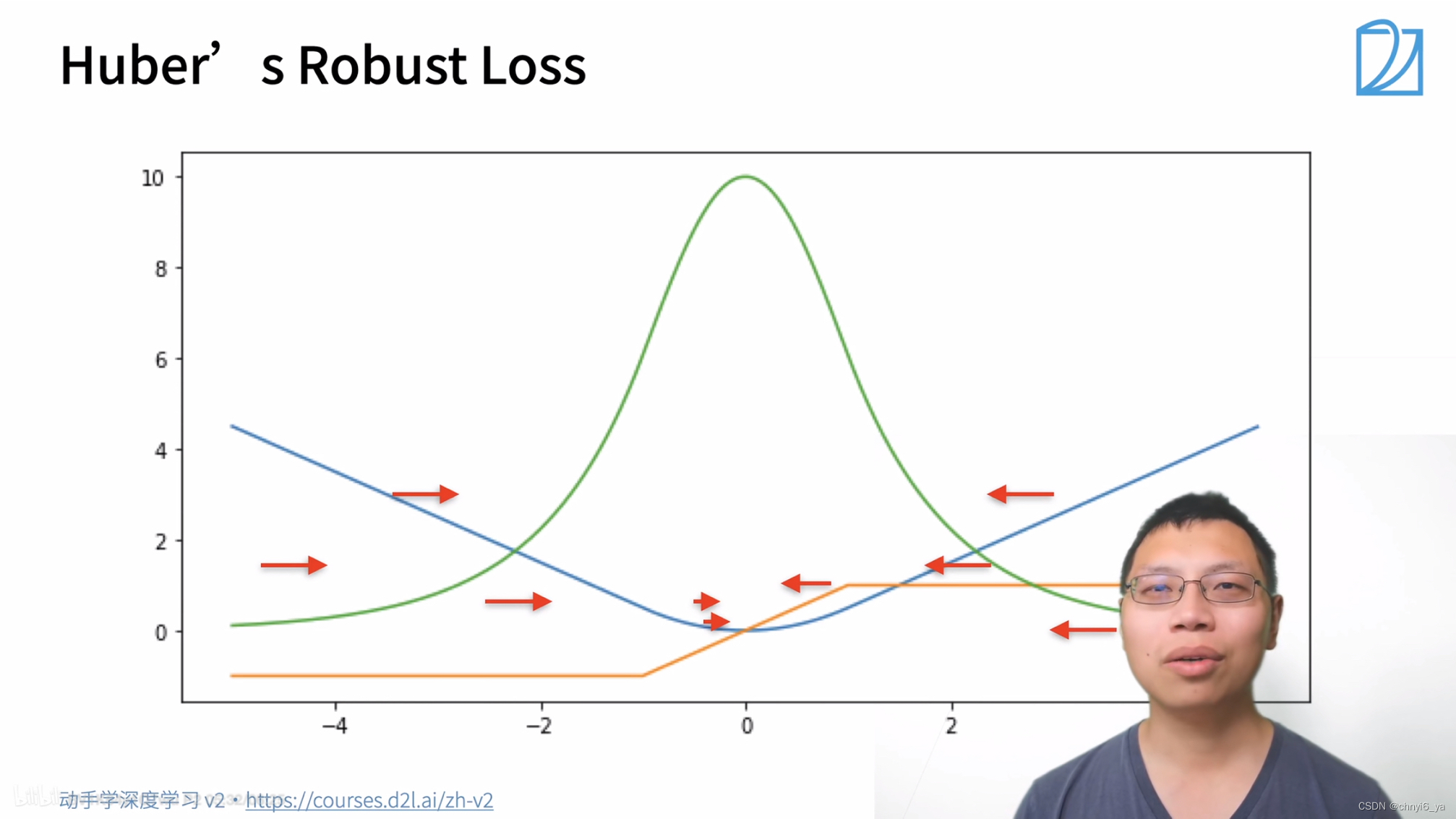
3. Huber‘s Robust Loss(鲁棒损失)
定义:当预测值和真实值差得比较大时,绝对值大于1时,是绝对值误差-1/2.当预测值和真实值靠的比较近的时候,就是平方误差。
好处是:当真实值和预测值差得比较远的时候,梯度是个固定值,用一个比较均匀的力度帮你往回拉,在比较靠近的时候,也就是优化末期的时候,梯度的绝对值会变得越来越小,这样可以保证优化是比较平滑的。