Bootstrap

遗传算法（Genetic Algorithm，GA）解决3维TSP问题

遗传算法（Genetic Algorithm，GA）是一种基于自然选择和遗传学原理的搜索和优化技术。它通常用于求解复杂的优化和搜索问题。遗传算法模拟生物进化过程，通过选择、交叉和变异操作逐步改进解决方案。

主要概念

  1. 个体（Individual）：一个可能的解决方案。
  2. 种群（Population）：一组个体。
  3. 基因（Gene）：个体的一部分，表示解决方案的某个参数。
  4. 染色体（Chromosome）：由多个基因组成的字符串，表示一个完整的解决方案。
  5. 适应度（Fitness）：衡量个体优劣的标准，适应度值越高，个体越优秀。

基本步骤

  1. 初始化种群：随机生成初始种群，包含若干个体。
  2. 计算适应度：评估每个个体的适应度值。
  3. 选择（Selection）：根据适应度值选择优良个体参与繁殖。常用的方法有轮盘赌选择、锦标赛选择等。
  4. 交叉（Crossover）：将选中的个体按一定概率进行交叉，生成新的个体。常用的方法有单点交叉、两点交叉和均匀交叉等。
  5. 变异（Mutation）：按一定概率对新个体的基因进行变异，以增加种群的多样性。常用的方法有位翻转、交换变异等。
  6. 生成新种群：将新生成的个体组成新的种群。
  7. 重复以上步骤：不断迭代，直到满足停止条件（如达到最大迭代次数或适应度值达到阈值）。

遗传算法的流程

  1. 种群初始化：随机生成初始种群。
  2. 适应度评估：计算每个个体的适应度。
  3. 选择操作：根据适应度选择优秀个体。
  4. 交叉操作：对选中的个体进行交叉，生成新个体。
  5. 变异操作：对新个体进行变异。
  6. 生成新种群：更新种群，进入下一代。
  7. 检查终止条件：如果满足终止条件，输出最优解；否则返回第2步。

应用领域

遗传算法广泛应用于以下领域：

  • 优化问题：如函数优化、参数优化等。
  • 组合优化：如旅行商问题（TSP）、背包问题等。
  • 机器学习：如特征选择、神经网络训练等。
  • 工程设计：如电路设计、结构优化等。

遗传算法因其通用性和鲁棒性，在许多复杂的优化问题中都表现出良好的性能。

使用遗传算法来解决3DTSP问题

这个代码实现了使用遗传算法（GA）来解决旅行商问题（TSP），通过模拟自然选择、交叉和变异过程，逐步优化路径长度。以下是代码的结构和主要过程的详细解释：

代码结构

  1. 数据加载和初始化
  2. 距离矩阵计算
  3. 初始种群生成
  4. 遗传算法主循环
  5. 路径长度计算与适应度评估
  6. 选择操作
  7. 交叉操作
  8. 变异操作
  9. 结果显示

主要过程

1. 数据加载和初始化
clc;
clear all;

file_path = '..\chapter2\data.csv';
Location = csvread(file_path, 1, 1);
N = size(Location, 1);  % TSP问题的规模
  • 加载数据文件，读取加工区域的坐标。
  • 确定问题规模 ( N )，即城市（加工区域）的数量。
2. 距离矩阵计算
D = zeros(N);  % 任意两个加工区域的距离间隔矩阵

for i = 1:N
    for j = 1:N
        D(i, j) = sqrt((Location(i, 1) - Location(j, 1))^2 + (Location(i, 2) - Location(j, 2))^2 + (Location(i, 3) - Location(j, 3))^2);
    end
end
  • 计算任意两个城市之间的欧氏距离，存储在距离矩阵 ( D ) 中。
3. 初始种群生成
NP = 500;  % 种群规模
G = 8000;  % 最大遗传代数
f = zeros(NP, N);  % 用于存储种群
F = [];  % 种群更新中间存储

for i = 1:NP
    f(i, :) = randperm(N);  % 随机生成初始种群
end

R = f(1, :);  % 存储最优种群
len = zeros(NP, 1);  % 存储路径长度
fitness = zeros(NP, 1);  % 存储归一化适应值
gen = 0;
  • 初始化种群规模 ( NP ) 和最大遗传代数 ( G )。
  • 随机生成初始种群，每个个体是一个城市序列。
4. 遗传算法主循环
while gen < G
  • 主循环继续进行，直到达到最大代数 ( G )。
5. 路径长度计算与适应度评估
    for i = 1:NP
        len(i, 1) = D(f(i, N), f(i, 1));
        for j = 1:(N-1)
            len(i, 1) = len(i, 1) + D(f(i, j), f(i, j+1));
        end
    end
    maxlen = max(len);  % 最长路径
    minlen = min(len);  % 最短路径
    rr = find(len == minlen);
    R = f(rr(1, 1), :);
    for i = 1:length(len)
        fitness(i, 1) = 1 - ((len(i, 1) - minlen) / (maxlen - minlen + 0.0001));
    end
  • 计算每个个体（路径）的总长度，并找到最短路径和最长路径。
  • 根据路径长度计算适应度值。
6. 选择操作
    nn = 0;
    for i = 1:NP
        if fitness(i, 1) >= rand  % 基于概率的选择
            nn = nn + 1;
            F(nn, :) = f(i, :);
        end
    end
  • 根据适应度值进行选择操作，保留优秀个体。
7. 交叉操作
    [aa, bb] = size(F);
    while aa < NP
        nnper = randperm(nn);
        A = F(nnper(1), :);
        B = F(nnper(2), :);
        W = ceil(N / 10);  % 交叉点个数
        p = unidrnd(N - W + 1);  % 随机选择交叉范围，从p到p+W
        for i = 1:W
            x = find(A == B(p + i - 1));
            y = find(B == A(p + i - 1));
            temp = A(p + i - 1);
            A(p + i - 1) = B(p + i - 1); 
            B(p + i - 1) = temp;
            temp = A(x); 
            A(x) = B(y); 
            B(y) = temp;
        end
  • 随机选择两个个体进行交叉操作，交换部分基因序列。
8. 变异操作
        p1 = floor(1 + N * rand());
        p2 = floor(1 + N * rand());
        while p1 == p2
            p1 = floor(1 + N * rand());
            p2 = floor(1 + N * rand());
        end
        tmp = A(p1); 
        A(p1) = A(p2); 
        A(p2) = tmp;
        tmp = B(p1); 
        B(p1) = B(p2); 
        B(p2) = tmp;
        F = [F; A; B];
        [aa, bb] = size(F);
    end
    if aa > NP
        F = F(1:NP, :);  % 保持种群规模为NP
    end
    f = F;  % 更新种群
    f(1, :) = R;  % 保留每代最优个体
    clear F;
    gen = gen + 1;
    Rlength(gen) = minlen;
end
  • 随机选择基因进行变异操作，进一步增加种群的多样性。
  • 更新种群，保留最优个体。
9. 结果显示
figure;
hold on;
view(3);  % 设置为3D视图

for i = 1:N-1
    plot3([Location(R(i), 1), Location(R(i+1), 1)], [Location(R(i), 2), Location(R(i+1), 2)], [Location(R(i), 3), Location(R(i+1), 3)], 'bo-');
    pause(0.1);
end

plot3([Location(R(N), 1), Location(R(1), 1)], [Location(R(N), 2), Location(R(1), 2)], [Location(R(N), 3), Location(R(1), 3)], 'ro-');
pause(0.1);
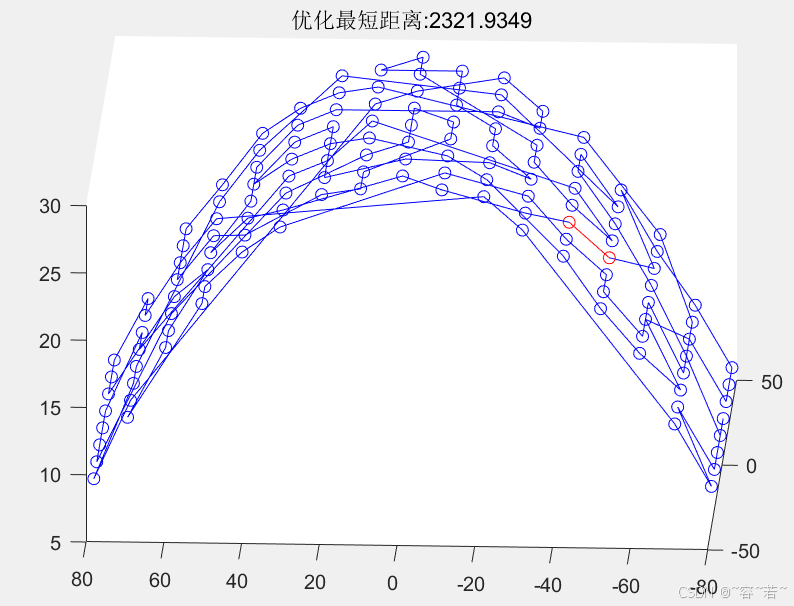
title(['优化最短距离:', num2str(minlen)]);

figure;
plot(Rlength);
xlabel('迭代次数');
ylabel('目标函数值');
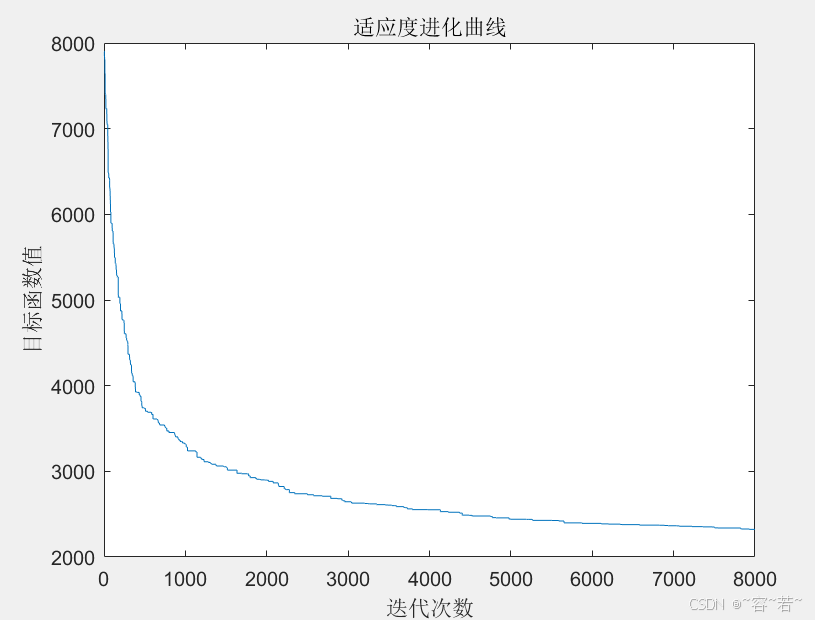
title('适应度进化曲线');
  • 绘制最终路径和适应度进化曲线，展示优化结果。

全部代码

clc;
clear all;
%%%%%%%%%绘制加工区域中心图%%%%%%%%%%%%%%%%%
file_path = '..\chapter2\data.csv';
Location = csvread(file_path, 1, 1);
% figure
% for i = 1 : size(Location,1)
%     scatter3(Location(i,1),Location(i,2),Location(i,3),'blue','filled')
%     hold on;
% end
% xlabel('x');
% ylabel('y');
% zlabel('z');
% title("加工区域中心");
%%%%%%%%遗传算法解决TSP问题，假设加工区域开始在中心，且最后回到中心%%%%%%%%
N=size(Location,1);                    %TSP问题的规模
D=zeros(N);                     %任意两个加工区域的距离间隔矩阵
%%%%%%%%%%%%%%%%%%%%%求任意两个城市距离间隔矩阵%%%%%%%%%%%%%%%%%%%%%
for i=1:N
    for j=1:N
        D(i,j)=((Location(i,1)-Location(j,1))^2+(Location(i,2)-Location(j,2))^2+(Location(i,3)-Location(j,3)))^0.5;
    end
end
NP=500;                          %种群规模
G=8000;                          %最大遗传代数
f=zeros(NP,N);                   %用于存储种群
F=[];                            %种群更新中间存储
for i=1:NP
    f(i,:)=randperm(N);          %随机生成初始种群
end
R=f(1,:);                        %存储最优种群
len=zeros(NP,1);                 %存储路径长度
fitness=zeros(NP,1);             %存储归一化适应值
gen=0;
%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
while gen<G
    %%%%%%%%%%%%%%%%%%%%%计算路径长度%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:NP
        len(i,1)=D(f(i,N),f(i,1));
        for j=1:(N-1)
            len(i,1)=len(i,1)+D(f(i,j),f(i,j+1));
        end
    end
    maxlen=max(len);              %最长路径
    minlen=min(len);              %最短路径
    %%%%%%%%%%%%%%%%%%%%%%%%%更新最短路径%%%%%%%%%%%%%%%%%%%%%%%%%%
    rr=find(len==minlen);
    R=f(rr(1,1),:);
    %%%%%%%%%%%%%%%%%%%%%计算归一化适应值%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:length(len)
        fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.0001)));
    end
    %%%%%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    nn=0;
    for i=1:NP
        if fitness(i,1)>=rand %%基于概率的选择
            nn=nn+1;
            F(nn,:)=f(i,:);
        end
    end
    [aa,bb]=size(F);
    %%%补充新种群F的规模到NP
    while aa<NP
        nnper=randperm(nn);
        A=F(nnper(1),:);
        B=F(nnper(2),:);
        %%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%
        W=ceil(N/10);              %交叉点个数
        p=unidrnd(N-W+1);          %随机选择交叉范围，从p到p+W
        for i=1:W
            x=find(A==B(p+i-1));
            y=find(B==A(p+i-1));
            temp=A(p+i-1);
            A(p+i-1)=B(p+i-1); 
            B(p+i-1)=temp;
            temp=A(x); 
            A(x)=B(y); 
            B(y)=temp;
        end
        %%%%%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%%%%
        p1=floor(1+N*rand());
        p2=floor(1+N*rand());
        while p1==p2
            p1=floor(1+N*rand());
            p2=floor(1+N*rand());
        end
        tmp=A(p1); 
        A(p1)=A(p2); 
        A(p2)=tmp;
        tmp=B(p1); 
        B(p1)=B(p2); 
        B(p2)=tmp;
        F=[F;A;B];
        [aa,bb]=size(F);
    end
    if aa>NP
        F=F(1:NP,:);             %保持种群规模为n
    end
    f=F;                         %更新种群
    f(1,:)=R;                    %保留每代最优个体
    clear F;
    gen=gen+1
    Rlength(gen)=minlen;
end
figure;
hold on;

view(3); % Set the view to 3D

for i = 1:N-1
    plot3([Location(R(i),1), Location(R(i+1),1)], [Location(R(i),2), Location(R(i+1),2)], [Location(R(i),3), Location(R(i+1),3)], 'bo-');
 
    pause(0.1); % Pause for 0.5 seconds
end

plot3([Location(R(N),1), Location(R(1),1)], [Location(R(N),2), Location(R(1),2)], [Location(R(N),3), Location(R(1),3)], 'ro-');
pause(0.1); % Pause for 0.5 seconds
title(['优化最短距离:',num2str(minlen)]);
figure
plot(Rlength)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')

结果

在这里插入图片描述
在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
景区负氧离子监测站如何与景区管理相结合？
Mysql之正则函数REGEXP的使用，适合复杂查询条件
Groupings sets详解
2024网站动态文字广告安全检测跳转源码
STM32实现ADC采样
Redis实战篇--商户查询缓存
什么是图神经网络
（附源码）基于ssm的银行助学贷款管理系统的设计与实现-计算机毕设 01013
人工智能算法优化：数学建模与实战案例
【Go】使用Go语言连接mysql数据库
;