Bootstrap

蚁群算法（Ant Colony Optimization, ACO）解决三维TSP问题

蚁群算法（Ant Colony Optimization, ACO）是一种仿生算法，由意大利科学家Marco Dorigo在20世纪90年代初提出。它受到蚂蚁觅食行为的启发，主要用于解决组合优化问题。以下是蚁群算法的一些关键概念和特点：

关键概念

  1. 信息素（Pheromone）：蚂蚁在路径上留下的信息素痕迹，这些痕迹会引导其他蚂蚁选择路径。信息素浓度越高，路径被选择的概率越大。

  2. 路径选择：蚂蚁在寻找食物的过程中，根据路径上的信息素浓度和启发函数（通常是路径长度或路径质量）来选择路径。

  3. 信息素更新：当蚂蚁找到食物并返回巢穴后，它们会加强路径上的信息素，使得其他蚂蚁更容易选择这条路径。与此同时，信息素会随时间逐渐挥发，避免算法陷入局部最优解。

算法步骤

  1. 初始化：在所有路径上初始化信息素浓度。

  2. 构建解：每只蚂蚁根据信息素和启发函数选择路径，构建一个完整的解。

  3. 局部更新：在构建解的过程中，蚂蚁会更新路径上的信息素浓度。

  4. 全局更新：所有蚂蚁构建解之后，根据解的质量进行全局信息素更新，强化优质解对应的路径。

  5. 迭代：重复以上步骤，直到达到停止条件（如迭代次数或找到满意的解）。

应用领域

  • 旅行商问题（TSP）：寻找最短路径问题。
  • 车辆路径问题（VRP）：优化物流配送路径。
  • 网络路由优化：优化数据传输路径。
  • 调度问题：优化生产调度计划。
  • 图像处理：边缘检测和图像分割。

蚁群算法通过模拟蚂蚁群体的自组织行为，能够有效解决许多复杂的优化问题，具有较强的鲁棒性和适应性。

蚁群算法解决三维TSP问题代码

这段代码实现了蚁群算法（Ant Colony Optimization, ACO）来解决旅行商问题（Traveling Salesman Problem, TSP），并可视化了优化过程和结果。以下是对代码的详细介绍：

数据导入与初始化

clc;
clear all;
%%%%%%%%%绘制加工区域中心图%%%%%%%%%%%%%%%%%
file_path = '..\chapter2\data.csv';
Location = csvread(file_path, 1, 1);
  • 清空工作区和命令行。
  • 从指定路径加载数据文件，数据文件中的位置信息存储在 Location 变量中。

距离矩阵计算

n = size(Location, 1); % TSP问题的规模
D = zeros(n); % 任意两个加工区域的距离间隔矩阵

for i = 1:n
    for j = 1:n
        D(i,j) = ((Location(i,1)-Location(j,1))^2 + (Location(i,2)-Location(j,2))^2 + (Location(i,3)-Location(j,3)))^0.5;
    end
end
  • 计算任意两个位置间的距离，并存储在距离矩阵 D 中。

蚁群算法参数设置

m = 50; % 蚂蚁个数
Alpha = 1; % 信息素重要程度参数
Beta = 5; % 启发式因子重要程度参数
Rho = 0.1; % 信息素蒸发系数
G_max = 100; % 最大迭代次数
Q = 100; % 信息素增加强度系数
Eta = 1 ./ D; % Eta为启发因子，这里设为距离的倒数
Tau = ones(n,n); % Tau为信息素矩阵
Tabu = zeros(m, n); % 存储并记录路径的生成
NC = 1; % 迭代计数器
R_best = zeros(G_max, n); % 各代最佳路线
L_best = inf .* ones(G_max, 1); % 各代最佳路线的长度
figure(1); % 优化解
  • 设置蚁群算法的参数，包括蚂蚁数量、信息素重要程度、启发因子、信息素蒸发系数、最大迭代次数等。

主要算法循环

while NC <= G_max            
    % 将m只蚂蚁放到n个城市上
    Randpos = [];
    for i = 1:(ceil(m / n))
        Randpos = [Randpos, randperm(n)];
    end
    Tabu(:, 1) = (Randpos(1, 1:m))'; 

    % m只蚂蚁按概率函数选择下一座城市
    for j = 2:n
        for i = 1:m
            visited = Tabu(i, 1:(j-1)); % 已访问的城市
            J = zeros(1, (n - j + 1)); % 待访问的城市
            P = J; % 待访问城市的选择概率分布
            Jc = 1;
            for k = 1:n
                if length(find(visited == k)) == 0
                    J(Jc) = k;
                    Jc = Jc + 1;
                end
            end

            % 计算待选城市的概率分布
            for k = 1:length(J)
                P(k) = (Tau(visited(end), J(k)) ^ Alpha) * (Eta(visited(end), J(k)) ^ Beta);
            end
            P = P / (sum(P));

            % 按概率原则选取下一个城市
            Pcum = cumsum(P);
            Select = find(Pcum >= rand);
            to_visit = J(Select(1));
            Tabu(i, j) = to_visit;
        end
    end

    if NC >= 2
        Tabu(1, :) = R_best(NC - 1, :);
    end

    % 记录本次迭代最佳路线
    L = zeros(m, 1);
    for i = 1:m
        R = Tabu(i, :);
        for j = 1:(n - 1)
            L(i) = L(i) + D(R(j), R(j + 1));
        end
        L(i) = L(i) + D(R(1), R(n));
    end
    L_best(NC) = min(L);
    pos = find(L == L_best(NC));
    R_best(NC, :) = Tabu(pos(1), :);

    % 更新信息素
    Delta_Tau = zeros(n, n);
    for i = 1:m
        for j = 1:(n - 1)
            Delta_Tau(Tabu(i, j), Tabu(i, j + 1)) = Delta_Tau(Tabu(i, j), Tabu(i, j + 1)) + Q / L(i);
        end
        Delta_Tau(Tabu(i, n), Tabu(i, 1)) = Delta_Tau(Tabu(i, n), Tabu(i, 1)) + Q / L(i);
    end
    Tau = (1 - Rho) .* Tau + Delta_Tau;

    % 禁忌表清零
    Tabu = zeros(m, n);

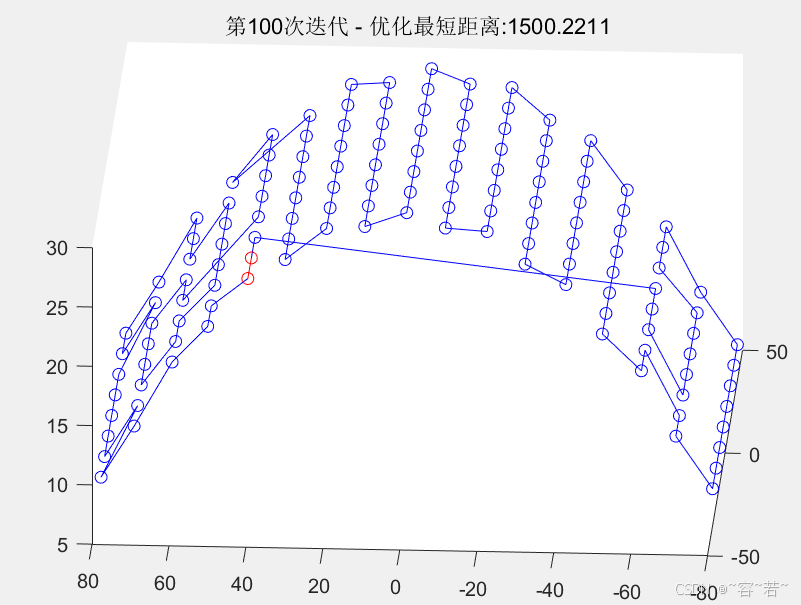
    % 绘制历代最优路线
    for i = 1:n-1
        plot3([Location(R_best(NC, i), 1), Location(R_best(NC, i + 1), 1)], [Location(R_best(NC, i), 2), Location(R_best(NC, i + 1), 2)], [Location(R_best(NC, i), 3), Location(R_best(NC, i + 1), 3)], 'bo-');
        hold on;
    end
    plot3([Location(R_best(NC, n), 1), Location(R_best(NC, 1), 1)], [Location(R_best(NC, n), 2), Location(R_best(NC, 1), 2)], [Location(R_best(NC, n), 3), Location(R_best(NC, 1), 3)], 'ro-');  
    title(['第', num2str(NC), '次迭代 - 优化最短距离:', num2str(L_best(NC))]);
    hold off;
    pause(0.005);
    NC = NC + 1;    
end
  • 蚂蚁从随机位置出发，按概率选择下一座城市。
  • 记录每次迭代的最佳路线，并更新信息素矩阵。
  • 可视化每次迭代的最优路线。

结果输出与绘图

Pos = find(L_best == min(L_best));
Shortest_Route = R_best(Pos(1), :); % 最佳路线
Shortest_Length = L_best(Pos(1)); % 最佳路线长度

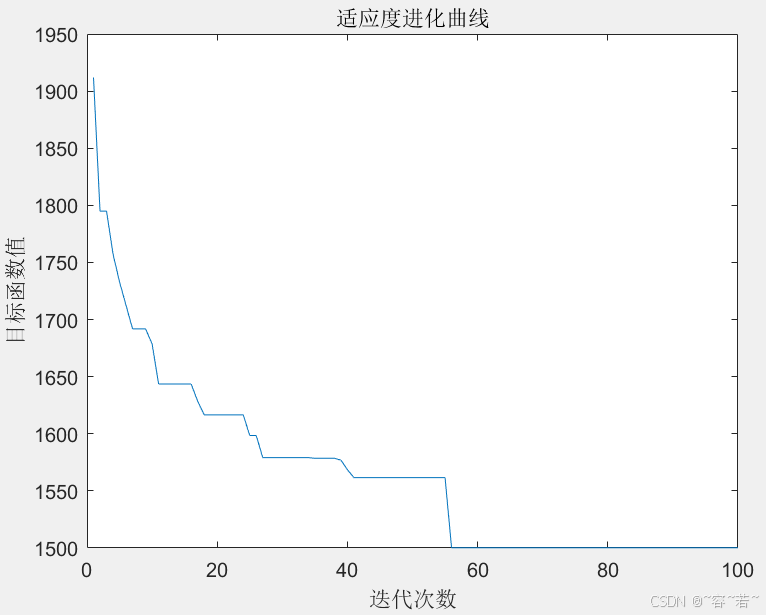
figure(2),
plot(L_best)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
  • 输出最佳路线和最短距离。
  • 绘制适应度进化曲线，显示目标函数值随迭代次数的变化。

全部代码

clc;
clear all;
%%%%%%%%%绘制加工区域中心图%%%%%%%%%%%%%%%%%
file_path = '..\chapter2\data.csv';
Location = csvread(file_path, 1, 1);
% figure
% for i = 1 : size(Location,1)
%     scatter3(Location(i,1),Location(i,2),Location(i,3),'blue','filled')
%     hold on;
% end
% xlabel('x');
% ylabel('y');
% zlabel('z');
% title("加工区域中心");
%%%%%%%%遗传算法解决TSP问题，假设加工区域开始在中心，且最后回到中心%%%%%%%%
n=size(Location,1);                    %TSP问题的规模
D=zeros(n);                     %任意两个加工区域的距离间隔矩阵
%%%%%%%%%%%%%%%%%%%%%求任意两个城市距离间隔矩阵%%%%%%%%%%%%%%%%%%%%%
for i=1:n
    for j=1:n
        D(i,j)=((Location(i,1)-Location(j,1))^2+(Location(i,2)-Location(j,2))^2+(Location(i,3)-Location(j,3)))^0.5;
    end
end
m=50;                     %蚂蚁个数
Alpha=1;                  %信息素重要程度参数              
Beta=5;                   %启发式因子重要程度参数
Rho=0.1;                  %信息素蒸发系数
G_max=100;                %最大迭代次数
Q=100;                    %信息素增加强度系数
Eta=1./D;                    %Eta为启发因子，这里设为距离的倒数
Tau=ones(n,n);               %Tau为信息素矩阵
Tabu=zeros(m,n);             %存储并记录路径的生成
NC=1;                        %迭代计数器
R_best=zeros(G_max,n);       %各代最佳路线
L_best=inf.*ones(G_max,1);   %各代最佳路线的长度
figure(1);%优化解
while NC<=G_max            
    %%%%%%%%%%%%%%%%%%第二步：将m只蚂蚁放到n个城市上%%%%%%%%%%%%%%%%
    Randpos=[];
    for i=1:(ceil(m/n))
        Randpos=[Randpos,randperm(n)];
    end
    Tabu(:,1)=(Randpos(1,1:m))'; 
    %%%%%第三步：m只蚂蚁按概率函数选择下一座城市，完成各自的周游%%%%%%
    for j=2:n
        for i=1:m
            visited=Tabu(i,1:(j-1));  %已访问的城市
            J=zeros(1,(n-j+1));       %待访问的城市
            P=J;                      %待访问城市的选择概率分布
            Jc=1;
            for k=1:n
                if length(find(visited==k))==0
                    J(Jc)=k;
                    Jc=Jc+1;
                end
            end
            %%%%%%%%%%%%%%%%%%计算待选城市的概率分布%%%%%%%%%%%%%%%%
            for k=1:length(J)
                P(k)=(Tau(visited(end),J(k))^Alpha)...
                    *(Eta(visited(end),J(k))^Beta);
            end
            P=P/(sum(P));
            %%%%%%%%%%%%%%%%按概率原则选取下一个城市%%%%%%%%%%%%%%%%
            Pcum=cumsum(P);
            Select=find(Pcum>=rand);
            to_visit=J(Select(1));
            Tabu(i,j)=to_visit;
        end
    end
    if NC>=2
        Tabu(1,:)=R_best(NC-1,:);
    end
    %%%%%%%%%%%%%%%%%%%第四步：记录本次迭代最佳路线%%%%%%%%%%%%%%%%%%
    L=zeros(m,1);
    for i=1:m
        R=Tabu(i,:);
        for j=1:(n-1)
            L(i)=L(i)+D(R(j),R(j+1));
        end
        L(i)=L(i)+D(R(1),R(n));
    end
    L_best(NC)=min(L);
    pos=find(L==L_best(NC));
    R_best(NC,:)=Tabu(pos(1),:);
    %%%%%%%%%%%%%%%%%%%%%%%%%第五步：更新信息素%%%%%%%%%%%%%%%%%%%%%%
    Delta_Tau=zeros(n,n);
    for i=1:m
        for j=1:(n-1)
            Delta_Tau(Tabu(i,j),Tabu(i,j+1))=...
                Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
        end
        Delta_Tau(Tabu(i,n),Tabu(i,1))=...
            Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
    end
    Tau=(1-Rho).*Tau+Delta_Tau;
    %%%%%%%%%%%%%%%%%%%%%%%第六步：禁忌表清零%%%%%%%%%%%%%%%%%%%%%%
    Tabu=zeros(m,n);
    %%%%%%%%%%%%%%%%%%%%%%%%%历代最优路线%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:n-1
        plot3([ Location(R_best(NC,i),1), Location(R_best(NC,i+1),1)],...
            [Location(R_best(NC,i),2), Location(R_best(NC,i+1),2)],...
            [Location(R_best(NC,i),3), Location(R_best(NC,i+1),3)],'bo-');
        hold on;
    end
    plot3([Location(R_best(NC,n),1), Location(R_best(NC,1),1)],...
        [Location(R_best(NC,n),2), Location(R_best(NC,1),2)], ...
        [Location(R_best(NC,n),3), Location(R_best(NC,1),3)],'ro-');  
    title(['第', num2str(NC), '次迭代 - 优化最短距离:', num2str(L_best(NC))]);
    hold off;
    pause(0.005);
    NC=NC+1;    
end
%%%%%%%%%%%%%%%%%%%%%%%%%%第七步：输出结果%%%%%%%%%%%%%%%%%%%%%%%%%%
Pos=find(L_best==min(L_best));
Shortest_Route=R_best(Pos(1),:);            %最佳路线
Shortest_Length=L_best(Pos(1));             %最佳路线长度
figure(2),
plot(L_best)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')

结果

在这里插入图片描述
在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
Kafka搭建(集群版)
springCloud微服务系列——链路跟踪第四篇——hystrix链路跟踪器
keras实现swin_transformer
Python导入csv数据画对比柱状图
oracle11G已正常开启监听服务，但oracle client远程连接仍无监听程序
基于ssm+vue基于Vue技术的流浪动物管理系统的设计与实现【开题+程序+论文】-计算机毕业设计
python torch.optim模块
IPython 使用技巧整理
数据中台-让数据用起来-第一章笔记
JVM（二、类加载系统）
;