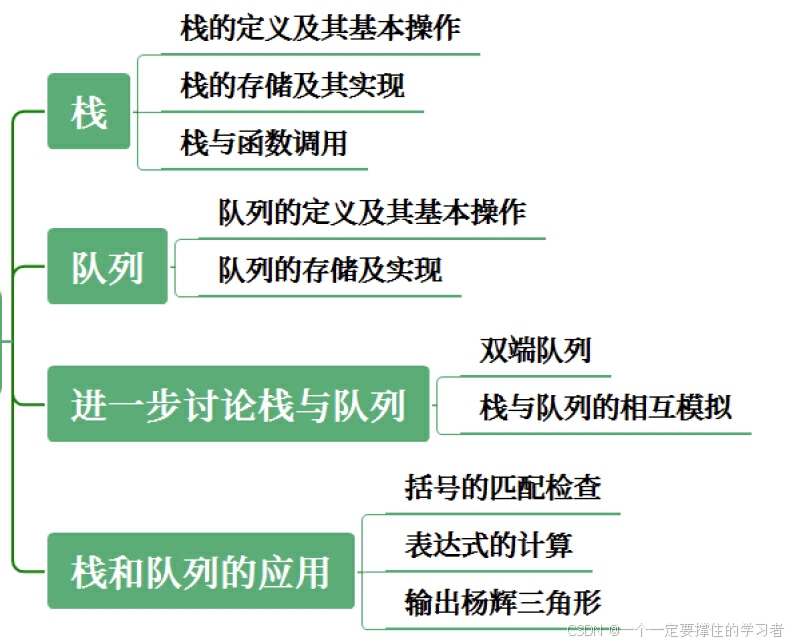
第三章栈和队列总览

第一节栈概览

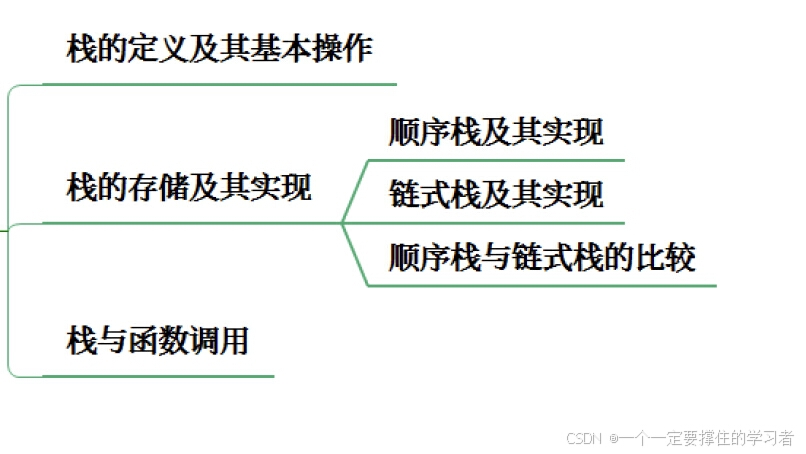
栈的定义及其基本操作

栈是一 种特殊的线性表，

它的特殊性体现在操作的位置上。

在含n个元素的线性表中进行插入或删除时，操作位詈可以有n+1 个或n个。

• n+1是因为带头节点的单链表是不是

• 当将操作位詈限定在线注表的同一端时，得到的数据结构就是栈。

它是— 种受限的线性表。

定义3-1 栈是限定仅在一 端进行插入和删除的线性表。

能进行插入和删除的一 端称为栈顶，

​ 在栈顶插入一 个元素称为入栈，也称为进栈或压栈；

​ 从栈顶删除一 个元素称为出栈，也称为退栈。

另一 端称为栈底。

栈中最多能保存的元素个数称为栈的容量；

• 怎么和用顺序方式，也就是数组存储的线性表有点像呢，还有容量

  确实如此，顺序栈，就是用数组来存储的，所以数组大小，就是栈的容量

可以沿用线性表的表示方法，将栈S表示为：
$$\begin{gathered} S=(a_0,a_1,\cdots ,a_{n-1}) \\ 在这个表示中，将哪—端规定为栈顶都是可以的， \\ 通常指定a{n}_1一端为栈顶 \\ {a}_0一端是栈底。因为是a_0先进入，先开始，肯定是栈底了 \\ 栈中元素个数n称为栈的长度 \\ 当n=0时，称为空栈 \end{gathered}$$

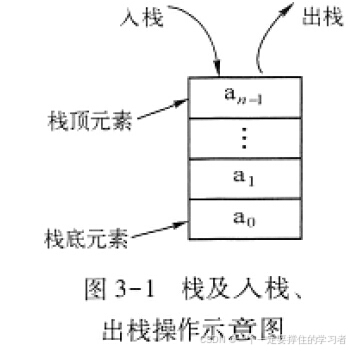
栈及入栈和出栈操作的示意图如图3-1所示

入栈橾作及出栈橾作只能在栈顶进行，实际上，只能看到栈顶元素，栈顶之下的所有元素都是不可见的，

即不允许访问非栈顶元素。

如何定义栈和栈的操作？合理的出栈序列个数如何计算？

栈中每个元素的类型都是ELEMType，定义如下。

typedef int ELEMType ;

栈的抽象数据类型为Stack，为简单起见，仅列出栈的基本操作如下：

int initStack(Stack * mys);
											// 初始化栈, 创建一个空栈mys
int clear(Stack * mys);
											// *、将栈mys清空
int pop(Stack * mys, ELEMTType * x);
											// 2、将栈顶元素出栈
int push(Stack * mys, ELEMTType x);
											// 1、将元素x入栈
int gettop(SeqStack * mys, ELEMTType * x);
											// 7、获取栈顶元素 (不出栈)
int isEmpty(Stack * mys);
											// 5、如果栈mys为空, 则返回1, 否则返回0
int isFull(Stack * mys);
											// 6、如果栈mys为满, 则返回1, 否则返回0

设有栈S，元素a0，a.，…，an-1依次入栈，然后依次出。

入时，首先a0入栈，然后a1入栈……最后an-1入栈。

出栈时，首先an-1出栈，然后an-2出栈……最后a0出栈。

得到的出栈次序刚好与入栈次序相反，最先入栈的元素最后出栈。

所以栈具有后进先出的特性。

对于栈，给定了入栈序列，是不是只能得到唯一的出栈序列?

一般来说，只要栈不空，就允许出栈;

只要栈不满，就允许入栈。

当没有其他的特殊限制时，对于同一个入栈序列，可能会得到很多个正确合理的出栈序列。

• 从另一方面来说，对于含n (n≥3) 个元素的入栈序列，它的**全排列共有n!**个。

• 这些序列不全是合理的出栈序列，实际上，合理的出栈序列个数为

$$\begin{gathered} （3-1）： \\ {C}_n=\frac{C_{2n}^n}{n+1} \end{gathered}$$

栈的两种存储方式及其实现？

和线性表一样，栈也有两种主要的存储方式，分别是顺序存储和链式存储。

顺序存储方式使用数组保存栈元素，得到的是顺序栈。

链式存储方式使用单链表保存栈元素，得到的是链式栈。

• 注意，是单链表，而不是什么双，循环之类的，应该会带头节点

顺序栈及其实现，还有对应时间复杂度

在顺序栈中，栈中的元素保存在一维数组中，为方便起见，将栈底定义在数组下标为0的位置。

同时还需要一个变量来标记栈顶的位置，即栈顶位置。

习惯上，栈顶位置也称为栈顶指针，

不过它只是数组中的一个下标，并不是真正意义上的一个指针。

顺序栈的定义如下

typedef int ELEMTType;  		 //以int类型为例
typedef struct {
    ELEMTType element[maxSize];  //maxSize是数组最大容量, 已定义的常量
    int top;  					 //栈顶位置
} SeqStack;  					 //顺序栈

顺序栈的基本操作如下。

int initStack(SeqStack * mys);
												// 初始化栈
int clear(SeqStack * mys);
												// *、将栈mys清空
int pop(SeqStack * mys, ELEMTType * x);
												// 2、将栈顶元素出栈
int push(SeqStack * mys, ELEMTType x);
												// 1、将元素x入栈
int gettop(SeqStack * mys, ELEMTType * x);
												// 7、获取栈顶元素 (不出栈)
int isEmpty(SeqStack * mys);
												// 5、如果栈mys为空, 则返回1, 否则返回0
int isFull(SeqStack * mys);
												// 6、如果栈mys为满, 则返回1, 否则返回0

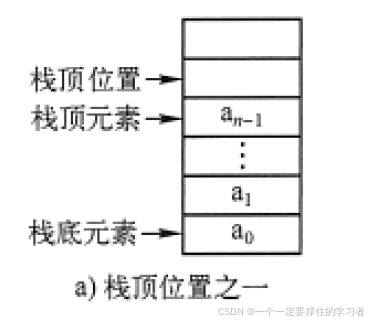
栈顶位置top具体指向数组中的哪个位置呢?

它有两种不同的定义方式，

• 一种是定义在紧邻栈顶元素的下一个空位置，如图3-4a所示;

本书实现时采用图34a所示的定义方式。

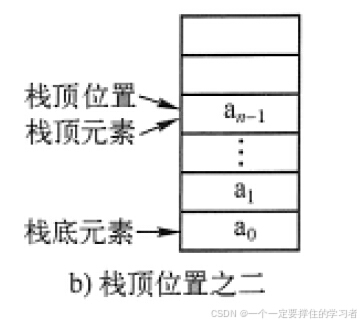
• 另一种是定义在栈顶元素所在的位置，如图3-4b所示。

*、清空栈，初始化栈

5、栈空，6、栈满

判定栈空及栈满等操作的时间复杂度也是O(1)。

入栈时，新元素放在element[top]处，然后top值加1，表明栈顶移向下一个位置，为下一次的入栈操作做好准备。

第一个元素入栈时放在数组下标为0的位置。

因为数组空间有限，最大容量是maxSize，所以入栈时需要判定栈是否是满的。

出栈时，需要先将top值减1，然后将element[top]处的值通过参数x返回。

与入栈操作时要判定栈是否为满类似，出栈时需要判定栈是否是空的。

top的值既是保存下一个入栈元素的位置，也是栈中所含元素个数的计数器，可谓“身兼数职”

1、入栈，2、出栈

因为栈的入栈操作及出栈操作都在栈顶进行，入栈及出栈时都不需要移动栈中已有的元素，避免了顺序表中插入及删除操作时的数据移动，

故顺序栈入栈操作、出栈操作及获取栈顶元素操作的时间复杂度都是O(1)。

有时，也可以将数组下标最大的一端作为栈底，入栈时，栈顶指针减1，出栈时，栈顶指针加1。

7、获取栈顶元素

另外，栈顶指针可以定义在栈顶元素所在的位置。

链式栈及其实现，还有对应时间复杂度

与顺序表类似，顺序栈也受数组大小的限制。

如果不能提前预知栈中元素的最大个数，就不能精确地设定maxSize的值，这种情况下可以使用链式栈。

链式栈，可以看作一个仅在表头位置进行操作的单链表。

将头指针所指的这一端作为栈顶，

表尾一端作为栈底。

入栈操作及出栈操作都可以通过头指针完成。

所以，在链式栈中，可以只定义头指针，尾指针及头结点 都可以不定义。

例如，图3-4a所示的顺序栈使用链式方式存储时，得到的链式栈如图3-7所示。

• 这是不带头节点的单链表

链式栈的基本操作要实现的基本功能与顺序栈的基本操作是一样的，但因为两种栈的存储方式不同，所以实现方式也不同。

*、初始化栈

2、出栈

与顺序栈一样，链式栈的入栈、出栈等操作的时间复杂度也都是O(1)。

*清空栈

1、入栈

与顺序栈一样，链式栈的入栈、出栈等操作的时间复杂度也都是O(1)。

5、栈空

顺序栈和链式栈的比较

实现顺序栈和链式栈的所有操作都只需要常数时间，因此栈的两种实现方式的优从前面的分析中知道，劣仅体现在它们的存储效率上。

顺序栈需要预先申请一个固定长度的一维数组，并自始至终全部占用。

​ 当栈中元素个数相对较少时，空间浪费较大。

虽然链式栈的长度可变，但是每个元素都需要一个指针域，这又产生了结构性空间开销。

​ 链式栈的空间可能会非常零碎，且需要在程序中动态申请及释放。

根据以上分析，两种实现方式在优劣方面没有本质差别，在实际中都可选用。

• 当不能预先估算出栈中元素最大个数时，只能使用链式栈，

• 而如果知道栈的最大元素个数，则可以使用顺序栈。

• 其实就和顺序表，链表的比较差不多

函数调用中的递归调用，为什么最适合采用栈来保存信息？

设计程序时不可避免地会出现函数调用，系统如何处理这些函数调用呢?

通常来讲，当遇到函数调用语句时，当前正在执行的函数被暂停，程序控制转去执行被调用的函数。

函数中直接或间接调用自身的函数称为递归函数，

和递归法类似，见，Day25-【13003】短文，有哪些设计策略？顺序存储链式存储和线性非线性结构考题解析？，中：递归法是什么？

​ 相应的函数调用称为递归调用。

以函数A调用函数B为例。

在函数A的语句序列中遇到调用函数B的语句时，函数A暂停，这个位置不妨称为断点。

接下来执行函数B的函数体。函数B执行完毕，程序又回到断点，继续执行函数A中后续的语句。

为了能让函数A接续执行，转去函数B之前的相关信息都要保存起来，其目的是从函数B返回后，这些信息逐一恢复，从而函数A能继续执行。

用什么结构来保存这些信息呢?

• 如果只有这一次函数调用，那么使用哪种数据结构来保存这些信息都不是问题。

关键是，函数调用可能是一系列的，甚至函数还可以调用自身，形成递归调用，这样的调用通常都不是一次性的，需要保存的信息会是一系列的。

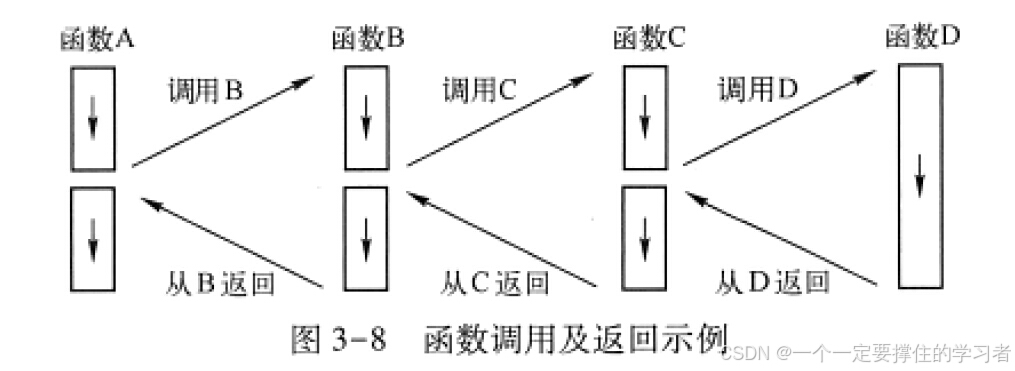
例如，函数A调用函数B，函数B又调用函数C，函数C又调用函数D，

这个调用过程如图3-8所示。

在图3-8所示的一系列函数调用中，系统需要依次保存函数A中的断点、函数B中的断点和函数C中的断点。

当函数D的执行结束后，最先返回到函数C中的断点继续执行，然后返回到函数B中的断点继续执行，最后返回到函数A中的断点继续执行。

可以看出，保存与恢复的次序刚好是互逆的。

这表明，栈是保存这些信息的最佳结构。

• ！流弊，原来栈这种数据结构，特别适合于函数调用，特别特别是递归调用

实际上，系统内部会开辟一个函数调用栈用来保存函数在调用过程中所需的一些信息。