unicycleKinematics
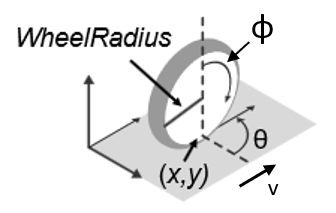
unicycleKinematics 创建了一个独轮车模型,用于模拟类似汽车的简化车辆动力学。车辆状态被定义为一个三元素向量 [x y theta],其中全局 xy 位置以米为单位,车辆航向角 theta 以弧度为单位。该模型近似于一个具有给定车轮半径(WheelRadius)的独轮车,它可以根据航向角(theta)原地旋转。要计算模型的时间导数状态,可使用导数函数,输入指令和机器人当前状态。
创建
语法
kinematicModel = unicycleKinematics
kinematicModel = unicycleKinematics(Name,Value)
描述
kinematicModel = unicycleKinematics 创建一个具有默认属性值的独轮车运动模型对象。
kinematicModel = unicycleKinematics(Name,Value) 将附加属性设置为指定值。可以任意顺序指定多个属性。
属性
WheelRadius - 车辆的车轮半径
0.1(默认) | 正数 值标量
车辆的车轮半径,单位为米。
WheelSpeedRange - 车轮速度范围
[-Inf Inf](默认) | 双元素向量
车速范围是一个双元素向量,提供最小和最大车速[MinSpeed MaxSpeed],单位为米/秒。
VehicleInputs - 车辆运动输入类型
"WheelSpeedHeadingRate"(默认) | 字符向量 | 字符串标量
VehicleInputs 属性用于指定使用derivative函数时模型输入命令的格式。选项指定为以下字符串之一:
"WheelSpeedHeadingRate" - 车轮速度和航向角速度,单位为弧度/秒。
"VehicleSpeedHeadingRate" - 车辆速度和航向角速度,单位为弧度/秒。
对象函数
derivative 车辆状态的时间导数
kinematicModel = unicycleKinematics; %定义一个机器人
initialState = [0 0 0]; %设置初始位置和方向
%模拟机器人运动
%将模拟时间跨度设置为 1 秒,时间步长为 0.05 秒,
%输入指令为 10 m/s,航向角速度为 pi/4 rad/s,以进行左转。
%使用求导函数 ode45 求解器模拟机器人的运动。
tspan = 0:0.05:1; %模拟的时间
inputs = [10 pi/4]; %匀速左转
[t,y] = ode45(@(t,y)derivative(kinematicModel,y,inputs),tspan,initialState);
%画图
figure
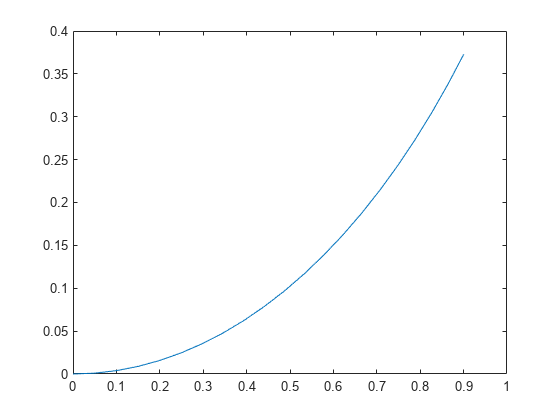
plot(y(:,1),y(:,2))运行结果
differentialDriveKinematics
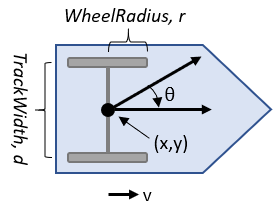
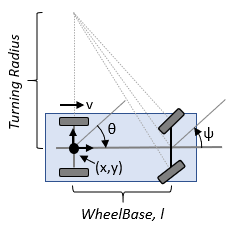
differentialDriveKinematics 可创建差速驱动车辆模型,模拟简化的车辆动力学。该模型近似于带有单个固定车轴的车辆,车轮之间有指定的轨道宽度。车轮可独立驱动。车速和方向由车轴中心确定。车辆状态被定义为一个三元素向量 [x y theta],其中全局 xy 位置以米为单位,车辆航向 theta 以弧度为单位。要计算模型的时间导数状态,可使用导数函数,输入指令和机器人当前状态。
创建
语法
kinematicModel = differentialDriveKinematics
kinematicModel = differentialDriveKinematics(Name,Value)
描述
kinematicModel = differentialDriveKinematics 将创建具有默认属性值的差分驱动运动模型对象。
kinematicModel = differentialDriveKinematics(Name,Value) 将对象上的属性设置为指定值。可以任意顺序指定多个属性。
属性
WheelRadius - 车辆的车轮半径
0.05(默认值) | 正数 值标量
车辆的车轮半径,单位为米。
WheelSpeedRange - 车轮速度范围
[-Inf Inf](默认) | 双元素向量
车速范围是一个双元素向量,提供最小和最大车速[MinSpeed MaxSpeed],单位为米/秒。
TrackWidth - 车轴上车轮之间的距离
0.2(默认值) | 正数值标量
车辆轨道宽度指车轮之间的距离或车轴长度,单位为米。
VehicleInputs - 车辆运动输入类型
"WheelSpeeds"(默认) | 字符向量 | 字符串标量
VehicleInputs 属性用于指定使用导数函数时模型输入命令的格式。选项指定为以下字符串之一:
"WheelSpeeds" - 每个车轮的角速度,单位为弧度/秒。
"VehicleSpeedHeadingRate" - 车辆速度和航向角速度,分别以米/秒和弧度/秒为单位。
kinematicModel = differentialDriveKinematics;%定于一个机器人
initialState = [0 0 0]; %设置初始位置和方向
%模拟机器人运动
%将模拟时间跨度设为 1 秒,时间步长为 0.05 秒,
%输入指令左轮为 50 rad/s,右轮为 40 rad/s,以实现右转。
%使用导数函数上的 ode45 求解器模拟机器人的运动。
tspan = 0:0.05:1;
inputs = [50 40]; %左轮转得更快
[t,y] = ode45(@(t,y)derivative(kinematicModel,y,inputs),tspan,initialState);
%画图
figure
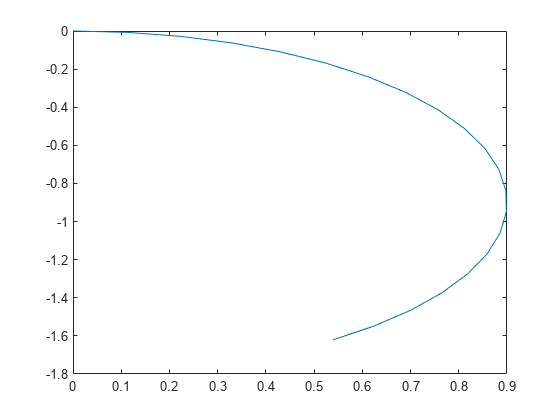
plot(y(:,1),y(:,2))
运行结果
bicycleKinematics
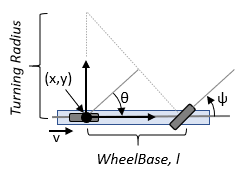
bicycleKinematics 创建了一个自行车车辆模型,用于模拟类似汽车的简化车辆动力学。该模型表示车辆的两个车轴之间有一定的距离,即轮距(WheelBase)。车辆状态被定义为一个三元素向量 [x y theta],其中全局 xy 位置以米为单位,车辆航向角 theta 以弧度为单位。前轮可通过转向角 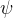
创建
语法
kinematicModel = bicycleKinematics
kinematicModel = bicycleKinematics(Name,Value)
描述
kinematicModel = bicycleKinematics 创建一个具有默认属性值的自行车运动模型对象。
kinematicModel = bicycleKinematics(Name,Value) 将附加属性设置为指定值。您可以按任意顺序指定多个属性。
属性
WheelBase - 前后轴之间的距离
1(默认) | 正数 值标量
轮距是指前后车轴之间的距离,单位为米。
VehicleSpeedRange - 车辆速度范围
[-Inf Inf](默认) | 正数标量
车辆速度范围是一个双元素向量,提供最小和最大车辆速度[MinSpeed MaxSpeed],单位为米/秒。
MaxSteeringAngle - 最大转向角
π/4(默认值) | 数值标量
最大转向角 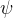
如果 MaxSteeringAngle 设置为 pi/2,则最小转弯半径值为 0。
MinimumTurningRadius - 最小车辆转弯半径
1.0000(默认值) | 数值标量
此属性为只读。
车辆最小转弯半径,以数字标量形式指定,单位为米。最小转弯半径使用轮距和最大转向角计算得出。
VehicleInputs - 车辆运动输入类型
"车辆速度转向角"(默认) | 字符向量 | 字符串标量
VehicleInputs 属性用于指定使用derivative函数时模型输入命令的格式。该属性有两个有效选项,分别指定为字符串或字符矢量:
"VehicleSpeedSteeringAngle" - 车辆速度和转向角
"VehicleSpeedHeadingRate" - 车辆速度和航向角速度
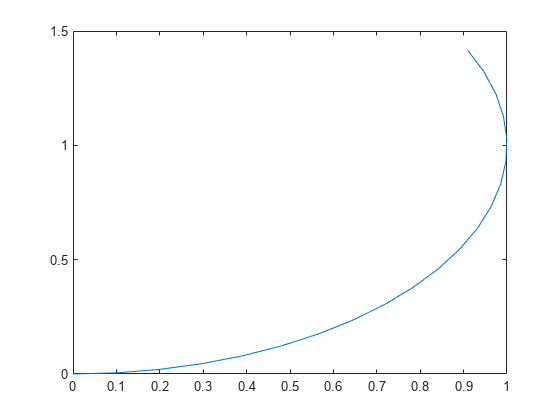
kinematicModel=bicycleKinematics; %定义一个机器人
initialState=[0 0 0]; %设置初始位置和方向
%模拟机器人运动
%将模拟时间跨度设为 1 秒,时间步长为 0.05 秒,
%输入指令为 2 米/秒的车速和 pi/4 弧度的转向角,以创建一个左转弯。
%使用导数函数上的 ode45 求解器模拟机器人的运动。
tspan=0:0.05:1;
inputs=[2 pi/4]; %左转弯
[t y]=ode45(@(t,y)derivative(kinematicModel,y,inputs),tspan,initialState);
%画图
figure
plot(y(:,1),y(:,2))运行结果
ackermannKinematics
ackermannKinematics 创建了一个使用阿克曼转向系统的汽车模型。该模型表示车辆的两个车轴之间的距离(WheelBase)。车辆的状态被定义为一个四元素向量 [x y theta 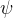
创建
语法
kinematicModel = ackermannKinematics
kinematicModel = ackermannKinematics(Name,Value)
描述
kinematicModel = ackermannKinematics 以默认属性值创建阿克曼运动模型对象。
kinematicModel = ackermannKinematics(Name,Value) 将附加属性设置为指定值。可以任意顺序指定多个属性。
属性
WheelBase - 前后轴之间的距离
1(默认) | 正数值标量
轮距是指前后车轴之间的距离,单位为米。
VehicleSpeedRange - 车辆轮速范围
[-Inf Inf](默认) | 双元素向量
车辆速度范围是一个双元素向量,提供最小和最大车辆速度[MinSpeed MaxSpeed],单位为米/秒。
%模拟移动机器人的不同运动模型
% 该示例展示了如何在一个环境中建立不同的机器人运动学模型,
% 并对它们进行比较。
% 用运动学约束条件定义移动机器人
% 有许多方法可以建立移动机器人的运动学模型。
% 所有方法都规定了车轮速度与机器人状态的关系:
% [x y theta],即 xy 坐标和以弧度为单位的机器人航向 theta。
% 独轮车运动学模型
% 表示移动机器人车辆运动学的最简单方法是使用独轮车模型,
% 该模型的车轮速度由围绕中心轴的旋转来设定,并可围绕 Z 轴转动。
% 差速驱动和自行车运动学模型都可以简化为独轮车运动学模型,
% 前提是输入的是车辆速度和车辆速度,而不考虑其他约束条件。
unicycle = unicycleKinematics("VehicleInputs","VehicleSpeedHeadingRate");
% 差速器传动运动学模型
% 差速驱动车型使用后驱动桥来控制车速和压头率。驱动桥上的车轮可以双向旋转。
% 由于大多数移动机器人都有一些与低级车轮命令的接口,
% 该模型将再次使用车辆速度和航向率作为输入,以简化车辆控制。
diffDrive = differentialDriveKinematics("VehicleInputs","VehicleSpeedHeadingRate");
% 为了将这种行为与独轮车模型区分开来,可在差速驱动运动学模型中添加车轮速度约束条件
diffDrive.WheelSpeedRange = [-10 10]*2*pi;
% 自行车运动模型
% 自行车模型将机器人视为一个类似汽车的模型,有两个车轴:
% 一个是后驱动车轴,另一个是绕 Z 轴转动的前车轴。
% 自行车模型的工作假设是,每个车轴上的车轮都可以建模为一个居中的车轮,
% 并且可以像自行车一样直接设置前轮的方向。
bicycle = bicycleKinematics("VehicleInputs","VehicleSpeedHeadingRate","MaxSteeringAngle",pi/8);
% 其他模型
% 阿克曼运动学模型是一种假设阿克曼转向的改进型类汽车模型。
% 在大多数类似汽车的车辆中,前轮并不围绕同一轴线转动,
% 而是在略微不同的轴线上转动,以确保它们围绕车辆转弯中心的同心圆行驶。
% 这种转动角度上的差异被称为阿克曼转向,在实际车辆中通常是通过机械装置来实现的。
% 从车辆和车轮运动学的角度来看,可以通过将转向角作为速率输入来实现。
carLike = ackermannKinematics;
% 设置模拟参数
% 这些移动机器人将沿着一组航点前进,这些航点旨在显示不同运动学造成的一些差异。
waypoints = [0 0;
0 10;
10 10;
5 10;
11 9;
4 -5];
% 定义总时间和采样率
sampleTime = 0.05; % 采样时间 [s]
tVec = 0:sampleTime:20; % 时间数组
initPose = [waypoints(1,:)'; 0]; % 初始姿势(x y theta)
% 创建车辆控制器
% 车辆使用 "纯粹追逐 "控制器跟踪一组航点。
% 给定一组航点、机器人当前状态和一些其他参数后,控制器会输出车辆速度和航向率。
% 定义控制器 每个机器人都需要自己的控制器
controller1 = controllerPurePursuit("Waypoints",waypoints,"DesiredLinearVelocity",3,"MaxAngularVelocity",3*pi);
controller2 = controllerPurePursuit("Waypoints",waypoints,"DesiredLinearVelocity",3,"MaxAngularVelocity",3*pi);
controller3 = controllerPurePursuit("Waypoints",waypoints,"DesiredLinearVelocity",3,"MaxAngularVelocity",3*pi);
% 使用 ODE 求解器模拟模型
%
% 使用导数函数对模型进行模拟,以更新状态。
% 本示例使用常微分方程 (ODE) 求解器生成解决方案。
% 另一种方法是使用循环更新状态,如《差分驱动机器人的路径跟踪》中所示。
%
% 由于 ODE 求解器要求将所有输出作为单一输出提供,
% 因此必须将纯粹的追逐控制器封装在一个函数中,
% 将线速度和航向角速度作为单一输出输出。
% 为此,我们使用了一个示例辅助函数 exampleHelperMobileRobotController。
% 示例助手还确保机器人在目标指定半径内停止。
goalPoints = waypoints(end,:)';
goalRadius = 1;
% 每种类型的模型都会调用一次 ode45。
% 导数函数根据 initPose 设置的初始状态计算状态输出。
% 每个导数都接受相应的运动模型对象、当前机器人姿态和控制器在该姿态下的输出。
% 为运动控制下的每个运动模型计算轨迹
[tUnicycle, unicyclePose] = ode45(@(t,y)derivative(unicycle, y,exampleHelperMobileRobotController(controller1,y,goalPoints,goalRadius)),tVec,initPose);
[tBicycle, bicyclePose] = ode45(@(t,y)derivative(bicycle, y,exampleHelperMobileRobotController(controller2,y,goalPoints,goalRadius)),tVec,initPose);
[tDiffDrive,diffDrivePose] = ode45(@(t,y)derivative(diffDrive,y,exampleHelperMobileRobotController(controller3,y,goalPoints,goalRadius)),tVec,initPose);
% 绘制结果图
%
% 使用 plotTransforms 可以在一张图上轻松查看 ODE 求解器的结果,
% 从而一次性直观地看到所有轨迹的结果。
%
% 首先必须将姿态输出转换为平移和四元数的索引矩阵。
unicycleTranslations = [unicyclePose(:,1:2) zeros(length(unicyclePose),1)];
unicycleRot = axang2quat([repmat([0 0 1],length(unicyclePose),1) unicyclePose(:,3)]);
bicycleTranslations = [bicyclePose(:,1:2) zeros(length(bicyclePose),1)];
bicycleRot = axang2quat([repmat([0 0 1],length(bicyclePose),1) bicyclePose(:,3)]);
diffDriveTranslations = [diffDrivePose(:,1:2) zeros(length(diffDrivePose),1)];
diffDriveRot = axang2quat([repmat([0 0 1],length(diffDrivePose),1) diffDrivePose(:,3)]);
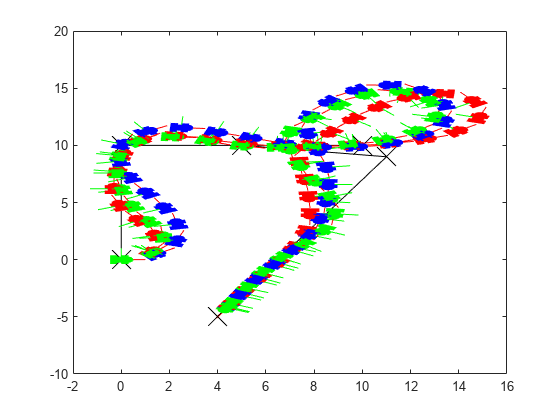
% 接下来,可以绘制所有变换的集合,并从顶部查看。
% 独轮车、自行车和差速驱动机器人的路径分别为红色、蓝色和绿色。
% 为了简化绘图,只显示每十个输出。
figure
plot(waypoints(:,1),waypoints(:,2),"kx-","MarkerSize",20);
hold all
plotTransforms( unicycleTranslations(1:10:end,:), unicycleRot(1:10:end,:),'MeshFilePath','groundvehicle.stl',"MeshColor","r");
plotTransforms( bicycleTranslations(1:10:end,:), bicycleRot(1:10:end,:),'MeshFilePath','groundvehicle.stl',"MeshColor","b");
plotTransforms(diffDriveTranslations(1:10:end,:),diffDriveRot(1:10:end,:),'MeshFilePath','groundvehicle.stl',"MeshColor","g");
view(0,90)
function robotRefState = exampleHelperMobileRobotController(purePursuitObj, robotPose, robotGoal, goalRadius)
% exampleHelperMobileRobotController 将纯粹追逐控制器的输出转换为单一输出
% 此函数接受纯粹追随控制器对象 PUREPURSUITOBJ 和受控机器人的当前姿态。
% 该函数将控制器的两个输出合并为一个 2x1 输出,
% 即 ROBOTREFSTATE。这样,控制器就可以轻松地与ode 求解器。
% 获取控制器输出
controller = purePursuitObj;
[vRef, wRef] = controller(robotPose);
% 达到目标后停止控制器
distanceToGoal = norm(robotPose(1:2) - robotGoal(:));
if distanceToGoal < goalRadius
vRef = 0;
wRef = 0;
end
robotRefState = [vRef; wRef];
end
运行结果
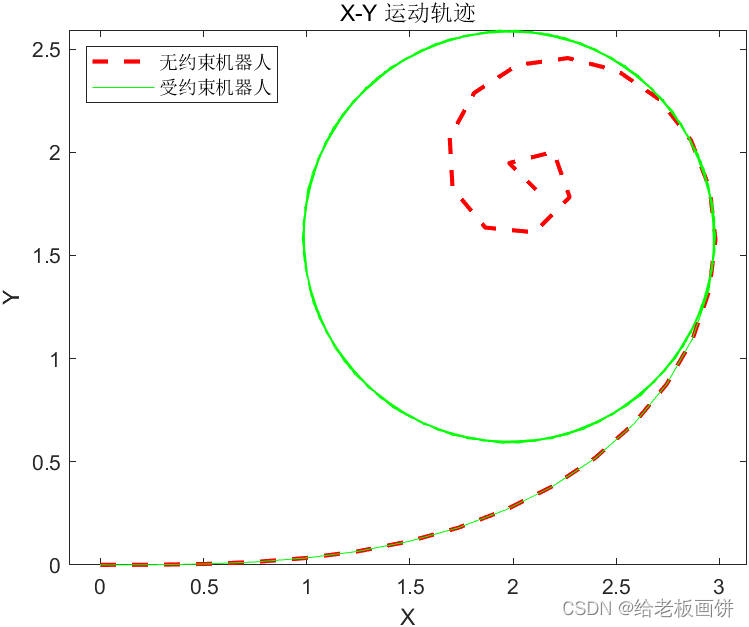
% 利用转向角约束模拟阿克曼运动模型
% 模拟一个使用阿克曼转向技术的移动机器人模型,并对其转向角度进行限制。
% 在模拟过程中,模型在达到转向极限后会保持最大转向角。
% 为了解转向饱和的影响,您可以比较两个机器人的轨迹,
% 其中一个有转向角限制,另一个没有任何转向限制。
% 定义模型
%
% 定义阿克曼运动模型。在这个类似汽车的模型中,前轮之间有一定的距离。
% 为了确保它们在同心圆上转动,车轮具有不同的转向角。
% 转弯时,前轮接收到的转向输入为转向角的变化率。
carLike = ackermannKinematics;
% 设置模拟参数
%
% 设置移动机器人以恒定线速度移动,并接收恒定转向率作为输入。
% 对受限机器人进行较长时间的模拟,以显示转向饱和。
velo = 5; % 恒定线速度
psidot = 1; % 恒定左转向率
% 定义总时间和采样率
sampleTime = 0.05; % 采样时间 [s]
timeEnd1 = 1.5; % 无约束机器人的模拟结束时间
timeEnd2 = 10; % 受约束机器人的模拟结束时间
tVec1 = 0:sampleTime:timeEnd1; % 无约束机器人的时间阵列
tVec2 = 0:sampleTime:timeEnd2; % 受约束机器人的时间阵列
initPose = [0;0;0;0]; % 初始姿势(x y theta phi)
% 为 ODE 求解器创建选项结构
%
% 在本例中,您需要将一个选项结构作为参数传递给 ODE 求解器。
% 该选项结构包含有关转向角限制的信息。
% 要创建选项结构,请使用 odeset 的 Events 选项和创建的事件函数 detectSteeringSaturation。
%
% 有关如何定义 detectSteeringSaturation 的说明,请参阅本示例末尾的定义事件函数。
options = odeset('Events',@detectSteeringSaturation);
% 使用 ODE 求解器模拟模型
%
% 接下来,您可以使用导数函数和 ODE 求解器 ode45 来求解模型并生成解决方案。
% 模拟无约束机器人
[t1,pose1] = ode45(@(t,y)derivative(carLike,y,[velo psidot]),tVec1,initPose);
% 模拟受约束机器人
[t2,pose2,te,ye,ie] = ode45(@(t,y)derivative(carLike,y,[velo psidot]),tVec2,initPose,options);
% 检测转向饱和度
%
% 当模型达到转向极限时,它会记录下事件的时间戳。达到极限的时间存储在 te 中。
if te < timeEnd2
str1 = "转向角达到极限值";
str2 = " 秒";
comp = str1 + te + str2;
disp(comp)
end
% 用新的初始条件模拟受约束机器人
%
% 现在,使用积分结束前的受约束机器人状态作为第二次模拟的初始条件。
% 修改输入矢量,以表示转向饱和状态,即把转向率设为零。
saturatedPsiDot = 0; % 饱和后的转向率
cmds = [velo saturatedPsiDot]; % 指令向量
tVec3 = te:sampleTime:timeEnd2; % 时间向量
pose3 = pose2(length(pose2),:);
[t3,pose3,te3,ye3,ie3] = ode45(@(t,y)derivative(carLike,y,cmds), tVec3,pose3, options);
% 绘制结果
%
% 使用 plot 和存储在姿势中的数据绘制机器人的轨迹。
figure(1)
plot(pose1(:,1),pose1(:,2),'--r','LineWidth',2);
hold on;
plot([pose2(:,1); pose3(:,1)],[pose2(:,2);pose3(:,2)],'g');
title('X-Y 运动轨迹')
xlabel('X')
ylabel('Y')
legend('无约束机器人','受约束机器人','Location','northwest')
axis equal
% 定义事件函数
% 设置事件函数,使积分在第 4 个状态 Theta 等于最大转向角时终止。
function [state,isterminal,direction] = detectSteeringSaturation(t,y)
maxSteerAngle = 0.785; % 最大转向角(pi/4 弧度)
state(4) = (y(4) - maxSteerAngle); % 当第 4 个状态 Theta 等于最大转向角时,饱和事件发生
isterminal(4) = 1; % 事件发生时终止集成
direction(4) = 0; % 双向终端
end