Update:9/10/2022 鸽了太久…增补了一些新的表述和简单推导，以及FFT在算法竞赛中的应用部分。帖子里的代码已经分别在2021全国大学生电子设计竞赛、洛谷OJ和课程设计中实战过，可靠性有保障。
Origin:10/23/2021 原始文章，刚学完FFT时做的一些笔记…漏洞挺多

原理

找一本数字信号处理的书，把DFT的原理耐心看一遍就能明白所有前置知识的概念，比如什么是W(N,nk），为什么要把实数序列拓展到复数域上，不要看xxx博文的介绍。FFT就是DFT的一种快速实现算法，DFT复杂度O($n^2$),FFT可以把复杂度降到O($nlogn$)。FFT分为基2 时间抽取法与基2 频率抽取法，本文介绍的是时间抽取法。
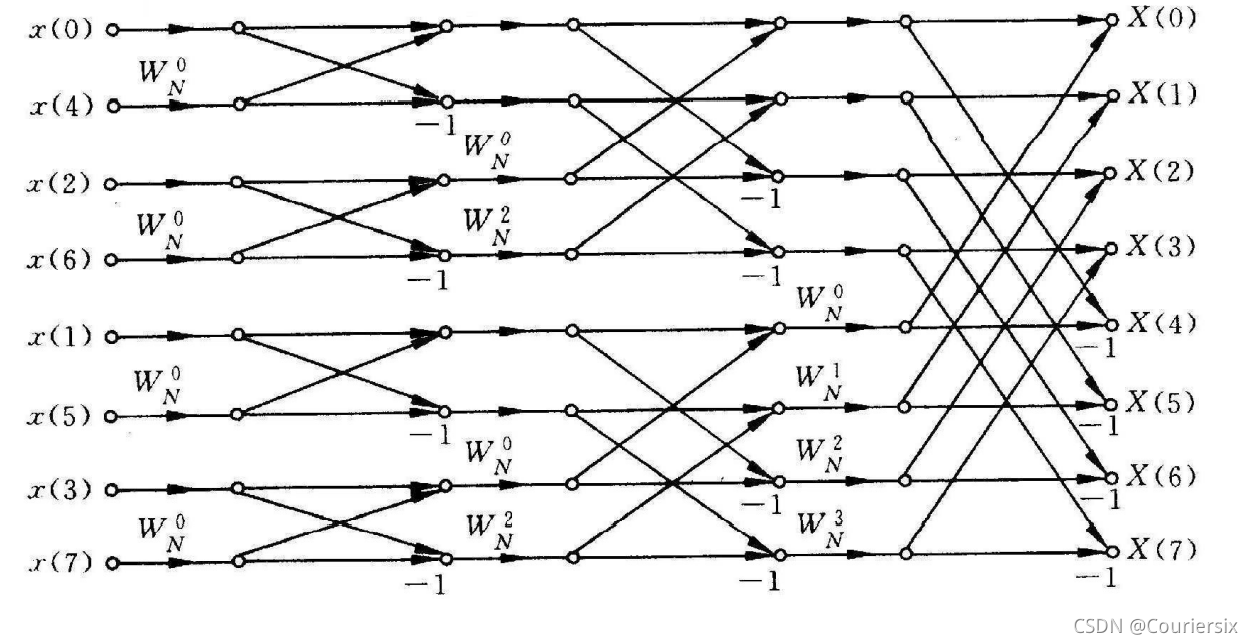
FFT的实现步骤主要分为三步:

• 将原序列扩展到复数域上，然后进行序数重排（元素的交换）
• 归一化蝶形系数
• 按照M级分解的顺序从左到右逐级进行蝶形运算

序数重排

就是把序列下标的二进制编码倒置，新序列x‘[i]=x[rev(i)],软件法或者硬件寻址法(比如DSP)都可以。

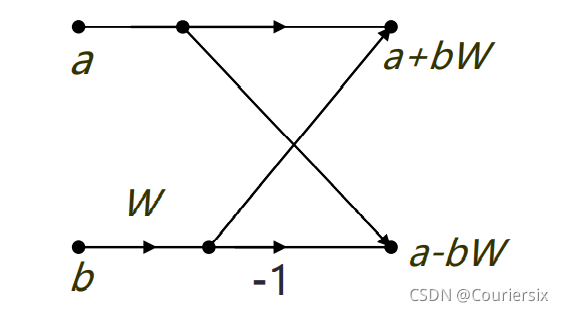
蝶形系数

W就是${W_{\frac{N}{2^{M-i}}}}^j$,

• ${W_A}^B=e^{-j\frac{2\pi B}{A}}$
• i是第i级蝶形计算$(1<=i<=M)$
• j是第i级蝶形运算的第j个W$(0<=j<=2^i)$
• $N=2^M$ （采样点数）

蝶形系数有三个重要性质:

• 周期性:${W_N}^n$ $={W_N}^{n+iN}$，i为整数。
• 可约性:${W_{mN}}^{kn}={W_{\frac{N}{k}}}^{\frac{n}{m}}$ m,k为任意整数。
• 共轭对称性:${W_N}^n={({W_N}^{-n})}^{\ast }$
• 正交性(这个主要是IFFT用，这里不作说明）。

这里主要用到可约性。我们可以把所有${W_{\frac{N}{2^{M-i}}}}^j$化为${W_N}^{j\cdot 2^{M-i}}$,这样，所有的${W_N}^i(0<=i<=N)$就可以直接预处理完成，蝶形计算中要用到的时候直接调用即可。

蝶形运算

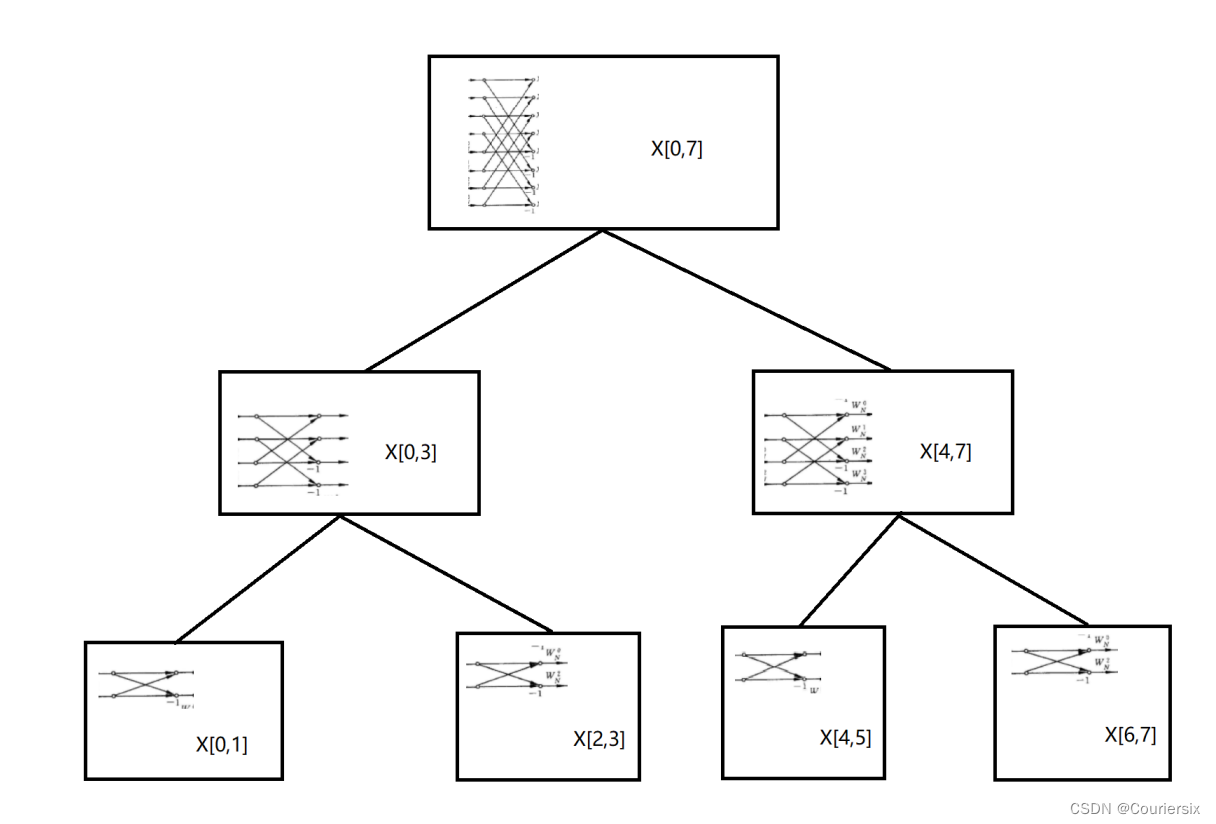
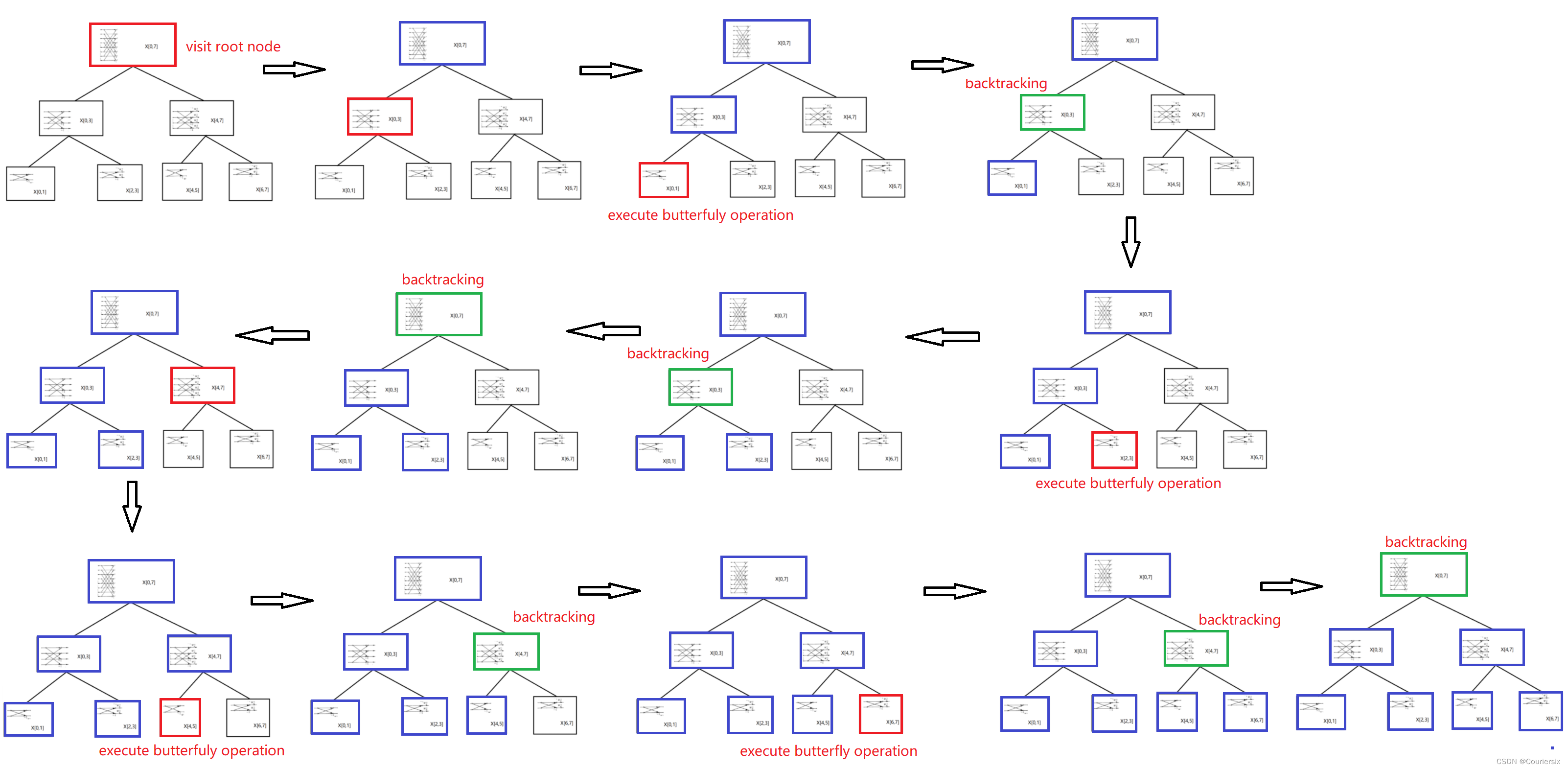
虽然FFT的原理是把每一级的序列细分为奇数下标组和偶数下标组，但由于FFT蝶形计算具有原位同址的特点，第 $i$ 级蝶形输出仅与第 $i-1$ 级的输入有关，所以我们不用关心每一级的第 $i$ 个位置上具体是 $x$ 序列中原本第几个元素，直接按照蝶形方向计算前进即可。我们可以观察到随着每一级的提升，蝶形会"膨胀"，第 $i$ 级一个蝴蝶结两端的间隔是 $2^{i-1}$。根据以上特征，将每一级的序列分治为两个处理区间 $[l,l+n-1]$ 和 $[l+n,r]$，使用递归法实现FFT核心程序，递归法的模型主要就是遍历区间的完全二叉树，以根节点为入口，遍历到每个叶子结点后进行最小蝶形子运算，然后再回溯更新其父节点区间，回溯到根节点即可得到输出序列，具体的实现过程如下所示:
首先，蝶形运算处理过程可以抽象为以下完全二叉树：

然后，整个蝶形运算的过程可以表示为：

典型应用

IFFT

有FFT变换自然就会有其逆变换IFFT，欣喜的是，IFFT也可以靠FFT算法实现！操作步骤如下：

1. 将频域序列X(k)取共轭
2. 直接对新序列进行FFT运算
3. 对输出序列取共轭再除以N，得到时域序列x(n)

数字信号处理中的频谱分析

举个例子，有了FFT，我们可以得到任意时刻音乐信号的实时频谱(音乐软件的特效也大多是FFT频谱可视化)，将信号的频谱分布得到后，我们就可以进行进一步的处理，比如加一个FIR数字滤波器，实现一个均衡器的功能。

算法竞赛

ACM和OI感觉还是用的挺多的…主要是用在快速求解多项式系数上(卷积）。作为EE人，个人不是很认同算法竞赛圈里普遍的复变函数推导FFT，感觉多少有点魔怔了，把简单问题复杂化。可以给一个信号处理视角的FFT卷积运算策略。
首先，两个序列 $x(n)$ 和 $h(n)$ 卷积 $x(n)\ast h(n)$这个操作看作是实现了一个FIR滤波器。
然后，我们把FFT的变换从数学中的实数域到复数域变换看成是时间域到频域的时频变换。
为什么信号处理中经常要考虑时频变换呢？因为一个时域信号的波形往往是很奇形怪状的，看不出什么花头，反而是频域信号，我们可以通过信号的频谱了解构成这个信号的各个频率分量。
下面给出一个信号与系统中的一个时频变换经典结论
$x(n)\ast h(n)<\frac{时频变换}{}>X(k)H(k)$
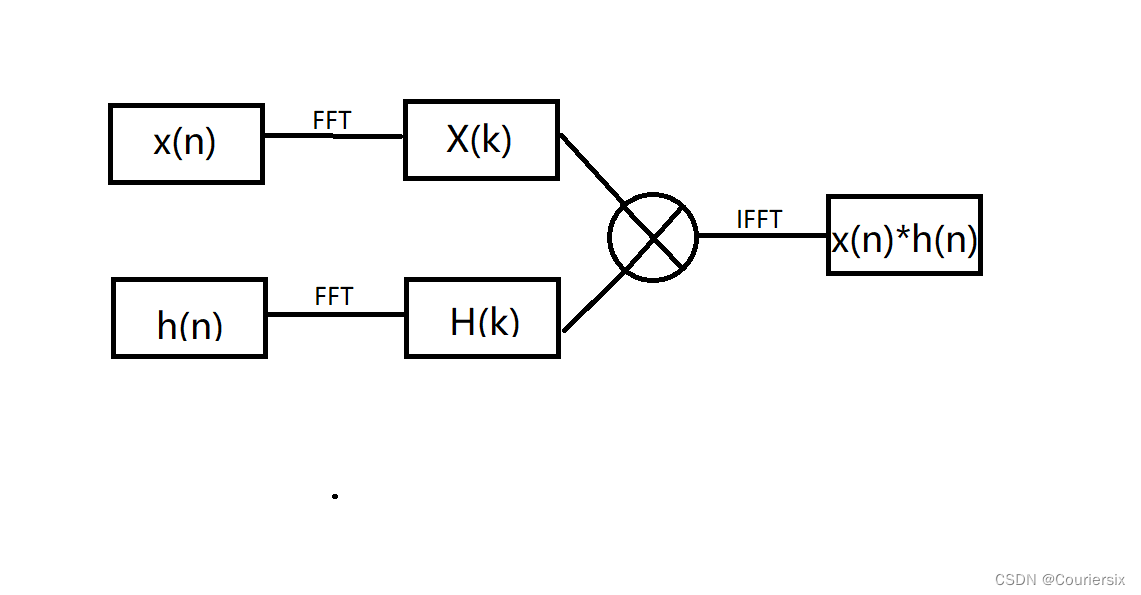
也就是说，时域里做卷积运算相当于频域里做乘积。
而FFT就是实现时频变换的好工具。
因此，快速求解 $x(n)\ast h(n)$ 的方法就变成了

洛谷模板Code:洛谷P3803 【模板】多项式乘法（FFT）
算法竞赛中FFT我自己接触的不是太多（太弱了摸不到做FFT的题捏），但了解了一下似乎是能实现大整数乘法、还有动态规划决策求解（货币系统类问题）。
不过听打ACM的朋友说现在FFT已经成每个队都会的签到题了？？？？

代码实现

递归法实现（不是最好的方法，但是最直观的）
ST官方库有一个用纯汇编实现的FFT，72Mhz的单片机系统下只要4ms就能跑完1024点FFT，以后有机会去逆向一下嘻嘻。

#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define pi 3.1415926
using namespace std;

/***
Codes by LZH on 10/23/2021
***/

typedef struct Complex{
	double a,b; //a:real b:Imagine
}; 
const int N=1024; //Num of Sample Nodes
const double fs=2048; //Sample frequency
Complex x[N],u[N],W[N]; //x:the fft sequence 
const int resolution=fs/N; //Calculation frequency resolution

Complex comp_plus(Complex u,Complex v){
	Complex e;
	e.a=u.a+v.a; e.b=u.b+v.b;
	return e;
}

Complex comp_times(Complex u,Complex v){
	Complex e;
	e.a=u.a*v.a-u.b*v.b;
	e.b=u.a*v.b+u.b*v.a;
	return e;
}

Complex comp_minus(Complex u,Complex v){
	Complex e;
	e.a=u.a-v.a; e.b=u.b-v.b;
	return e;
}

void rev(){ //reverse the sequence in bit order.  
	int len=log2(N);
	int idd,ret,bit;
	for (int i=0; i<N; i++){
		idd=i; ret=0;
		for (int j=0; j<len; j++){
			ret = ret << 1;                 
         	bit = idd & 1;             
         	idd = idd >> 1;   
         	ret = bit | ret;          
		}
		u[i]=x[ret];
	}
	for (int i=0; i<N; i++)
		x[i]=u[i];
}

Complex Wn(double A,double B){  
	Complex u;
	u.a=cos((2*pi/A)*B); u.b=-sin((2*pi/A)*B);
	return u;
}

void fft(int l,int r,int len){
	Complex tmp;
	int n=len/2;
	if (len<2) return; //Level 1 

	fft(l,l+n-1,n); //even seg process 
	fft(l+n,r,n);	//odd seg process
	
	for (int i=l; i<=r; i++){
		if (i<l+n){
			u[i]=comp_plus(x[i],comp_times(W[(i-l)*(N/len)],x[i+n])); 
		}
		else{
			x[i]=comp_minus(x[i-n],comp_times(x[i],W[(i-n-l)*(N/len)]));
			x[i-n]=u[i-n];
		}
	}
	return;
}

int main(){
	for (int i=0; i<N; i++){
		double t=i/fs; //time resolution
		x[i].a=114*sin(2*pi*50*t)+514*sin(2*pi*152*t)+1919*sin(2*pi*536*t)+810*sin(2*pi*996*t); //Generate the original signal sequence and tranfer it to Complex number field
		x[i].b=0; //Im{x(n)}=0 
		W[i]=Wn(N,i); //e^-j((2*pi*i)/N)
	}
	
	rev(); //reverse the original order 
	fft(0,N-1,N);

	for (int i=0; i<N/2; i++){
		double u;
		u=sqrt(x[i].a*x[i].a+x[i].b*x[i].b);
		printf("%d %.3lf\n",i*resolution,u*2/N); //the real Ampltude of the signal is the Amp of fft sequence times 2 divide N.
	}
	
	return 0;
}

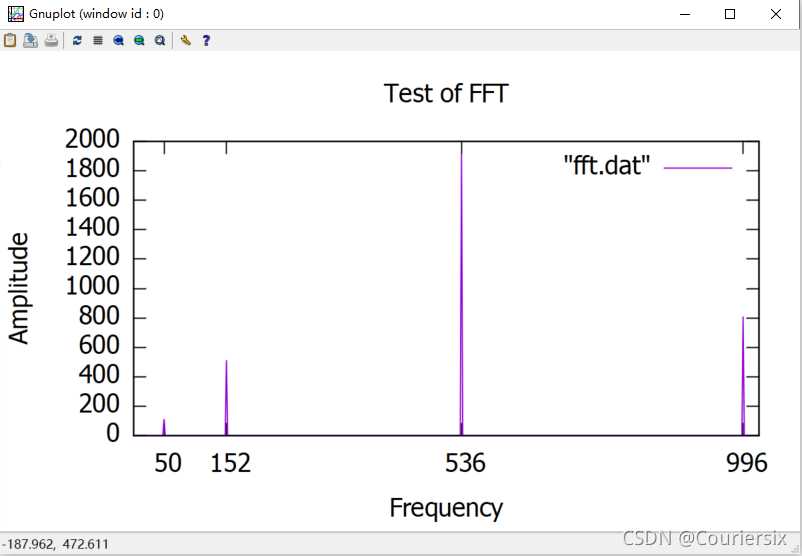
演示结果

上面的代码演示了采样点N=1024，采样频率=2048的FFT，原始信号是四个正弦信号的叠加，频率分别是:50,152,536,996；幅度是:114,514,1919,810。通过实验结果，我们可以发现FFT还是挺成功的，没有发生明显的频谱泄漏。这里要注意的是FFT中信号抽样依然要满足奈奎斯特采样定理 ($f_s>=2f_c$)。

FAQ

1.Q:为什么我用这套程序跑1000点的FFT会跟Matlab出来不一样？
A:帖子里给出的是基2 FFT，也是最常用的一种FFT。基2的含义是FFT运算的点数必须是 $2^n$ ，如果要运算1000点，请先通过补零将序列长度补充到1024，数字信号处理的知识告诉我们，对任意序列补零后再进行FFT运算，并不影响其运算结果。Matlab中任意点数的FFT是另外一种FFT的实现方法，实现过程相当复杂，暂时网络上没看到什么详细的开源工程。
2.Q：频谱泄露那么严重该怎么解决？
A：可以通过加窗进行改善。常用的有汉宁窗、海明窗、布莱克曼窗（幅值特性保留最好）。但是加窗之后会造成频谱能量的衰减，这是因为由帕萨瓦尔定理可知同一信号在时域内和频域内的总能量必然是相等的，但加窗这个过程是一种数学上的近似衰减，这必然会损失部分信号的原始能量。
3.Q：嵌入式系统的内存资源太紧张，FFT跑个1024点都很勉强怎么办？
A：这是工程上一个很常见的问题，嗯…内存优化，目前我只知道工程上64点FFT就够用了，好像需要对FFT进行改进一下进行等效操作…这个本科数字信号处理教材上还真没讲过…内存优化的话还是看看startup.s里怎么进行优化吧，实际项目中似乎启动用的汇编文件内存开销是最大的。
4.Q：上面的例子进一步加速的方法？
A：1.用循环版的非递归实现法。2.序列重排复杂度可以再降到 $O(n)$ , 具体可以参考OI Wiki上的方法。