.mat文件在Matlab中的读取使用操作

1. 数据中的采样频率为100Hz, 根据所分析的信号的特点确定合适的采样频率，截断长度（记录点数）

前言

mat数据格式是Matlab的数据存储的标准格式，.mat文件的方便之处在于其可以连同数据的变量名一同保存下来，并且不需要控制数据的存储格式，matlab会自动保存并区分我们所存储的内容，可以利用load指令可以实现对.mat文件的读取与使用。

利用load指令读取.mat文件：

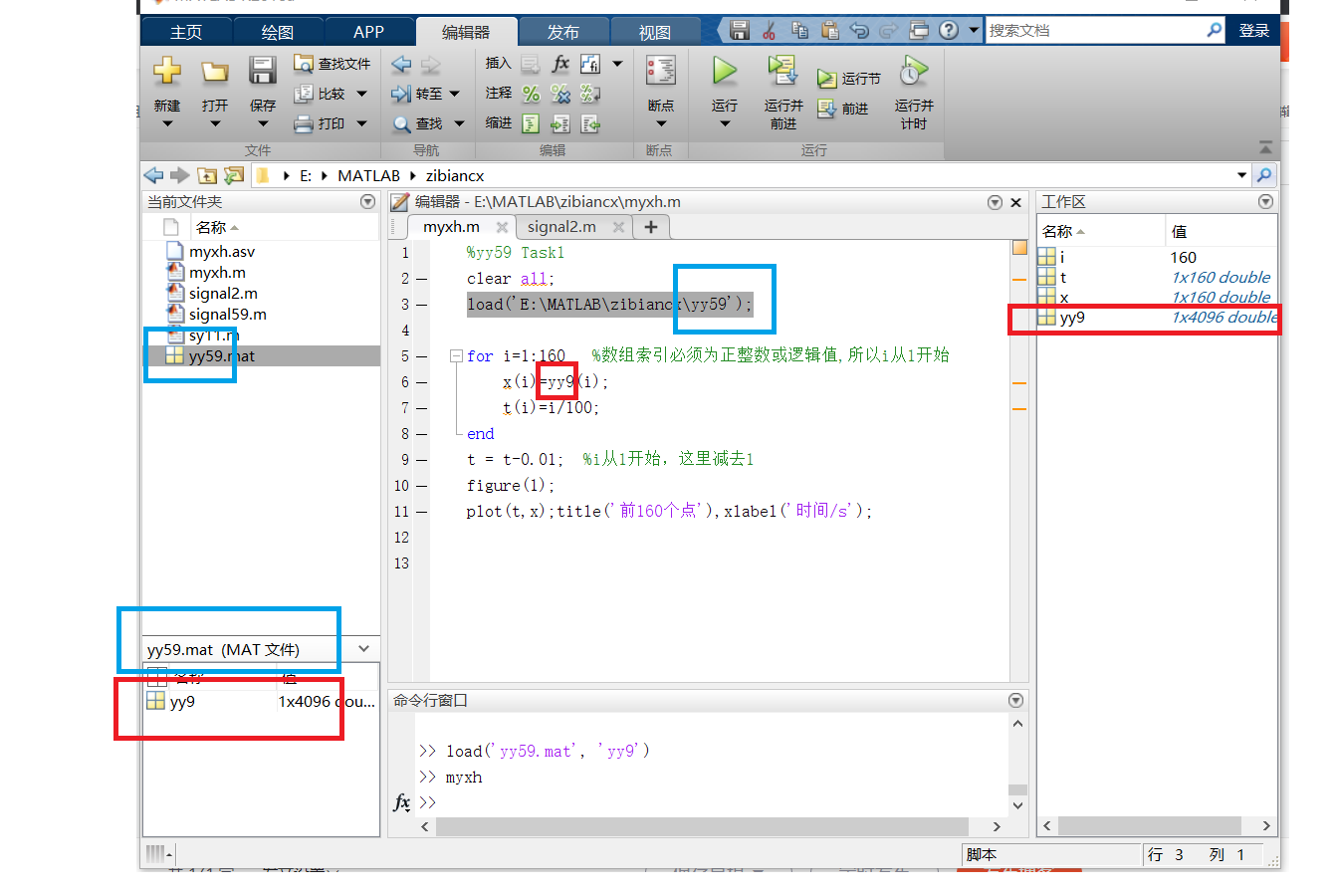
load('E:\文件名'); //不要加.mat后缀

以下图为例，读取并画出.mat文件中前160个点形成的波形。左侧双击.mat文件后，下方出现了mat文件内部变量的名称与类型，处理数据或读写的时候要以变量的名称来处理。

clear all;
load('E:\MATLAB\zibiancx\yy59');

for i=1:160   %数组索引必须为正整数或逻辑值,所以i从1开始
    x(i)=yy9(i);
    t(i)=i/100;
end
t = t-0.01;  %i从1开始，这里减去1
figure(1);
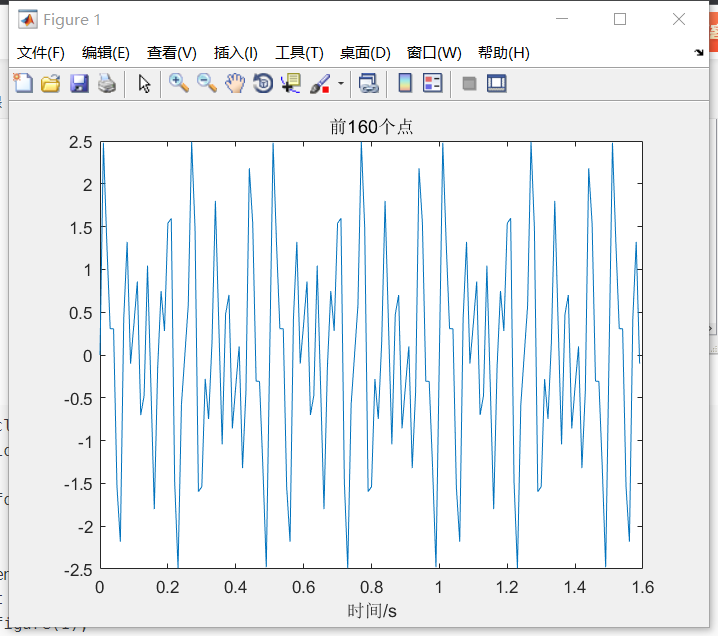
plot(t,x);title('前160个点'),xlabel('时间/s');

1. 数据中的采样频率为100Hz, 根据所分析的信号的特点确定合适的采样频率，截断长度（记录点数）

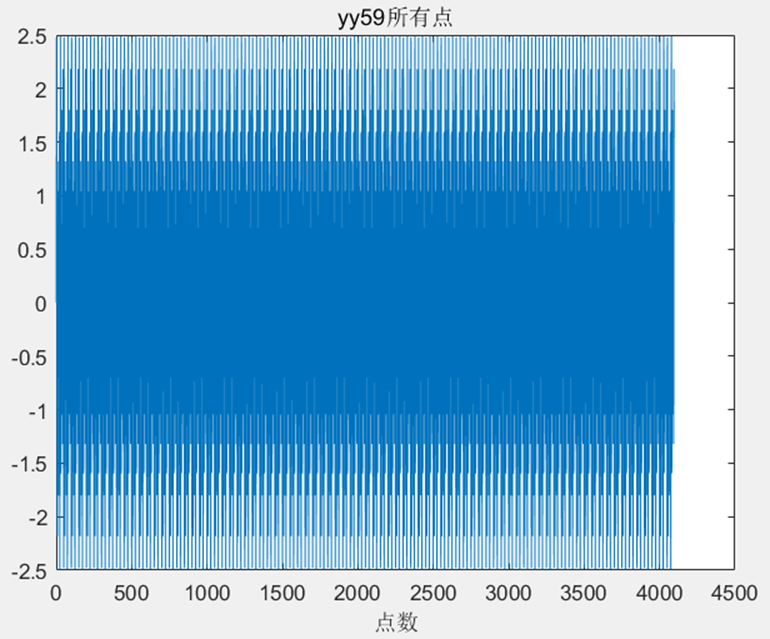
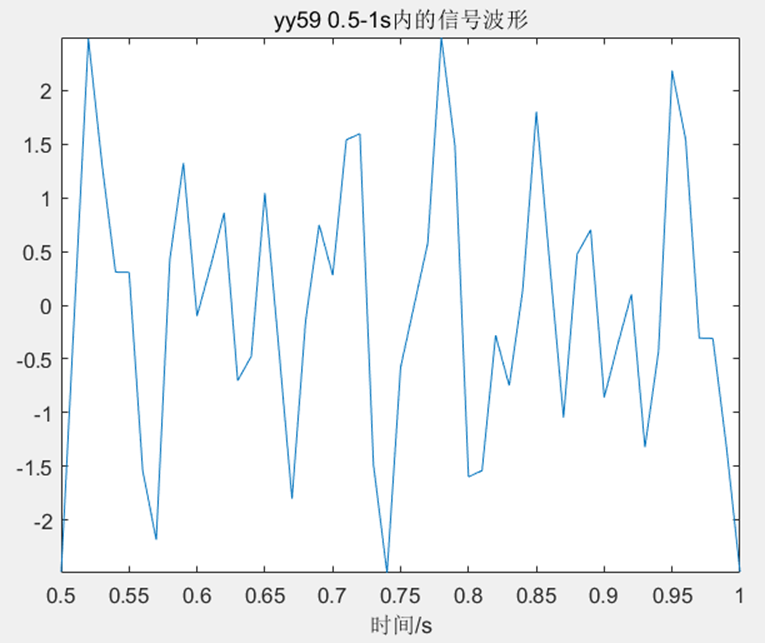
绘制出所有点的图，发现这是一个周期信号。原始信号采样频率100Hz，原始采样周期0.01s，结合前160点图进行分析发现信号周期约为0.5s，画出第50-100个点（0.5-1s）的波形如图所示：

%1.确定合适的采样频率，截断长度（记录点数）
clear all;
load('E:\MATLAB\zibiancx\yy59');
for i=1:4096
    x(i)=yy9(i);
    t(i)=i;
end
figure(2);
plot(t,x);title('yy59所有点'),xlabel('点数');

clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 50;    % 序列长度，每20点近似为一个周期
N = 50;    % 频率域采样个数，取N=L
for i=1:L+1    %取第50-100点进行处理
    x(i)=yy9(i+50);
    t(i)=i/Fs+0.5;
end
figure(3);
plot(t,x);title('yy59 0.5-1s内的信号波形'),xlabel('时间/s');

根据香农采样定理:如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样，那么原始模拟信号就能从采样产生的离散值中完全恢复。所以，先对信号进行DFT频域分析（2. 通过DFT频域分析方法，编程画出该信号的频谱与时域图形）获得频谱，该信号包含12Hz、16Hz、30Hz的信号，信号的最高频率分量为30Hz，所以采样频率应该大于等于60Hz，而给出的数据采样频率为100Hz，符合采样定理的要求。故采样频率沿用100Hz，截断长度（记录点数）取第51-100点，该部分点信号比较完整。

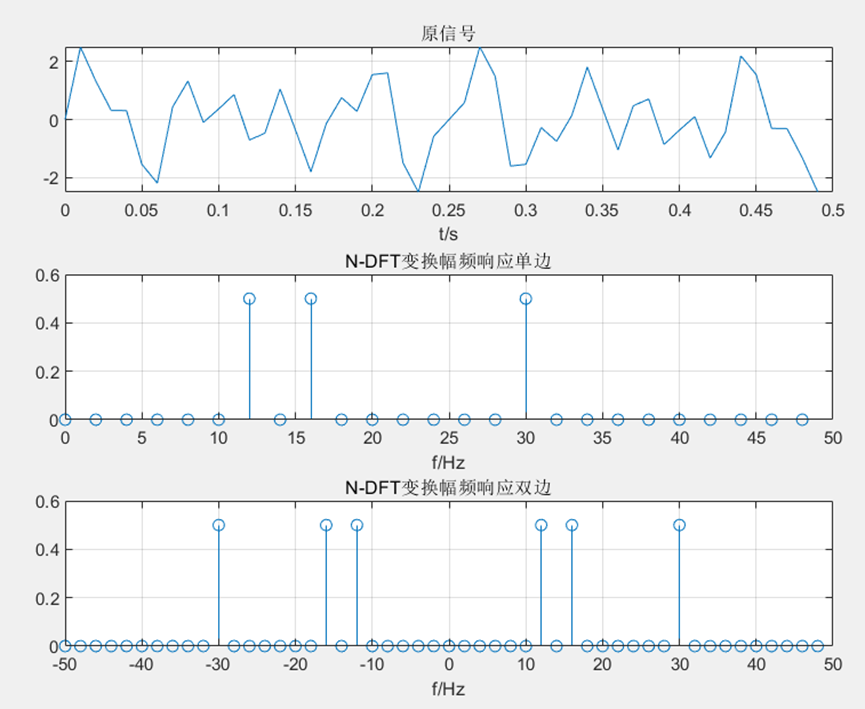
2. 通过DFT频域分析方法，编程画出该信号的频谱与时域图形

MATLAB的fft函数，其用法为Y=fft（x，N），其中x为原信号序列，Y为DFT（也就是FFT）变换后的，FFT与DFT等价，FFT为DFT的算法优化，fft函数中有三个参数：采样频率Fs，原序列长度L，N-DFT变换的N。令Fs=100(Hz)，L=50，N=50，对50—100点内的信号进行编程处理。

%2.DFT频域分析画出信号频谱
%DFT
clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 50;    % 原信号序列长度，每50点近似为一个周期
N = 50;    % 频率域采样个数，取N=L
t=(0:L-1).*Ts;%时域自变量
for i=1:L
    x(i)=yy9(i+50);
end%原信号
figure(4)
subplot(311);
plot(t,x);
title("原信号"),xlabel("t/s");
grid on;
Y=fft(x,N);%fft变换
Y=abs(Y)./N;%实际幅值变换
f=(0:N-1)*Fs./N;%实际频率变换
subplot(312);
stem(f(1:N/2),Y(1:N./2));
title("N-DFT变换幅频响应单边"),xlabel("f/Hz");
grid on;
f=f-Fs./2;%移位
subplot(313);
stem(f,fftshift(Y));%移位
title("N-DFT变换幅频响应双边"),xlabel("f/Hz");
grid on;
%时域内各分量与合成
clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 50;   % 使用原始序列个数，接近一个周期
for i=1:L
    x(i)=yy9(i+50);
    t(i)=i/Fs;
end
figure(5)
subplot(511);
t = t-Ts;
plot(t,x);title('原信号'),xlabel('时间/s');grid on
subplot(512);
t=(0:L-1).*Ts;
x=sin(12*2*pi*t);
plot(t,x,'r');title('12Hz分量'),xlabel('时间/s');grid on
subplot(513);
t=(0:L-1).*Ts;
x=sin(16*2*pi*t);
plot(t,x, 'g');title('16Hz分量'),xlabel('时间/s');grid on
subplot(514);
t=(0:L-1).*Ts;
x=sin(30*2*pi*t);
plot(t,x, 'b');title('30Hz分量'),xlabel('时间/s');grid on
subplot(515);
for i=1:L
    x(i)=yy9(i+50);
    t(i)=i/Fs;
end
t = t-Ts;
plot(t,x);title('合成'),xlabel('时间/s');hold on;
t=(0:L-1).*Ts;
x=sin(12*2*pi*t);
plot(t,x, 'r');hold on;
t=(0:L-1).*Ts;
x=sin(16*2*pi*t);
plot(t,x, 'g');hold on;
t=(0:L-1).*Ts;
x=sin(30*2*pi*t);
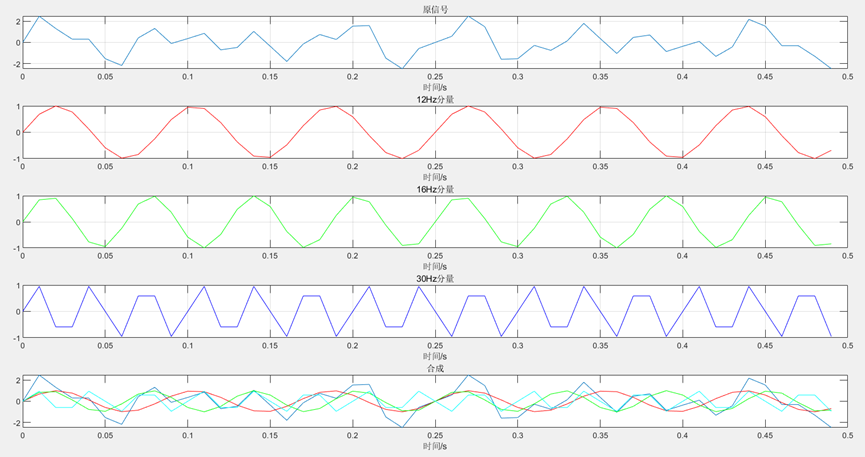
plot(t,x, 'c');hold on;

通过将一个周期的50个点进行DFT频域变换，分析发现该信号是由12Hz、16Hz和30Hz的频率信号组成的。下图为三个分量信号的时域图与叠加后的图像。

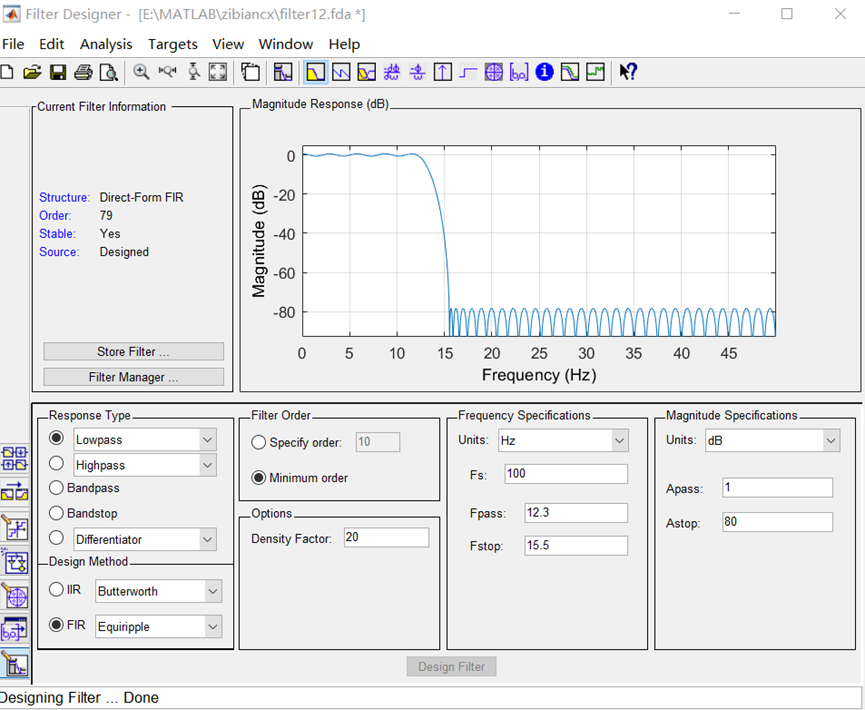
3. 使用滤波器设计方法将这些频率成分分别获得，并以图形显示

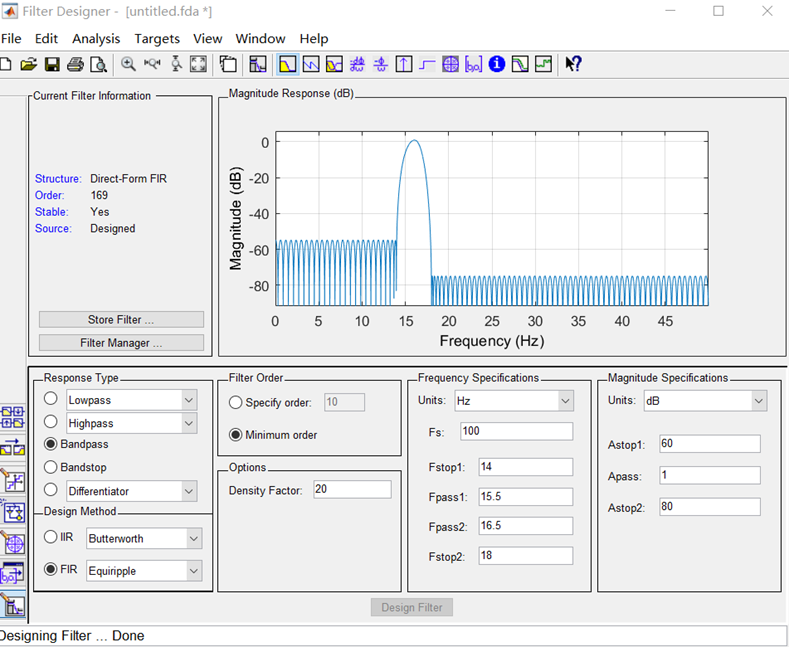
利用MATLAB Filter Designer设计低通滤波器对信号进行滤波。

%3.使用滤波器设计方法将这些频率成分分别获得，并以图形显示。
%12Hz
clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 160;   % 使用原始序列个数
for i=1:L
    y(i)=yy9(i);
    t(i)=i/100;
end

figure(6);
t = t-0.01;
subplot(311);
plot(t,y);title('时域原始信号'),xlabel('时间/s');hold on;

output = filter(filter12, y);
subplot(312);
t = t+0.01;
plot(t,output, 'b');title('时域滤波信号'),xlabel('时间/s');hold on;

y=sin(12*2*pi*t);
subplot(313);
plot(t,y, 'r');title('拟合信号(12Hz)'),xlabel('时间/s');
%16hz
clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 160;   % 使用原始序列个数
for i=1:L
    y(i)=yy9(i);
    t(i)=i/100;
end

figure(7);
t = t-0.01;
subplot(311);
plot(t,y);title('时域原始信号'),xlabel('时间/s');hold on;

output = filter(filter16, y);
subplot(312);
t = t+0.01;
plot(t,output, 'b');title('时域滤波后信号'),xlabel('时间/s');hold on;

y=sin(16*2*pi*t);
subplot(313);
plot(t,y, 'r');title('拟合信号(16Hz)'),xlabel('时间/s');
%30hz
clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 160;   % 使用原始序列个数
for i=1:L
    y(i)=yy9(i);
    t(i)=i/100;
end

figure(8);
t = t-0.01;
subplot(311);
plot(t,y);title('时域原始信号'),xlabel('时间/s');hold on;

output = filter(filter30, y);
subplot(312);
t = t+0.01;
plot(t,output, 'b');title('时域滤波后信号'),xlabel('时间/s');hold on;

y=sin(30*2*pi*t);
subplot(313);
plot(t,y, 'r');title('拟合信号(30Hz)'),xlabel('时间/s');

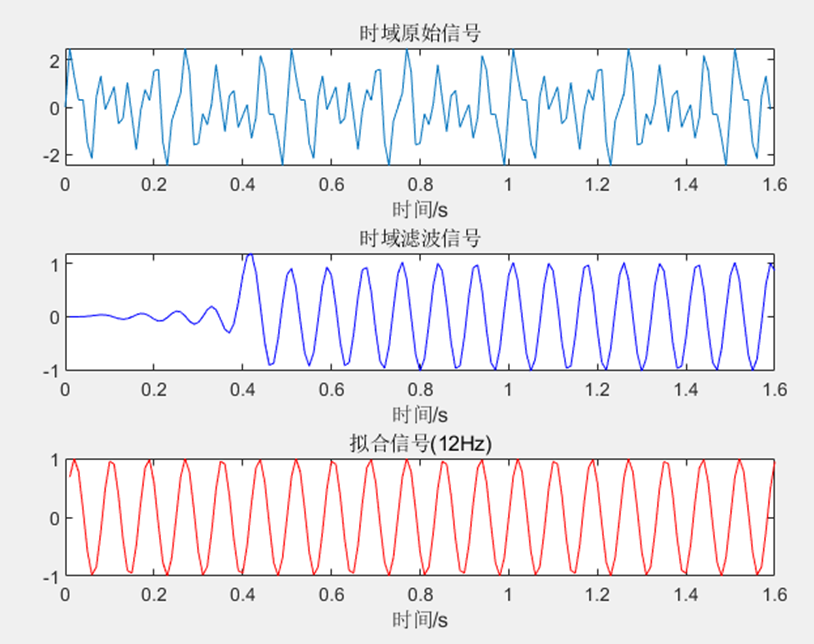
（1）12Hz低通滤波器：滤除16Hz和30Hz信号，如图所示，分别为时域原始信号，滤波后信号以及12Hz正弦产生信号用来对比。

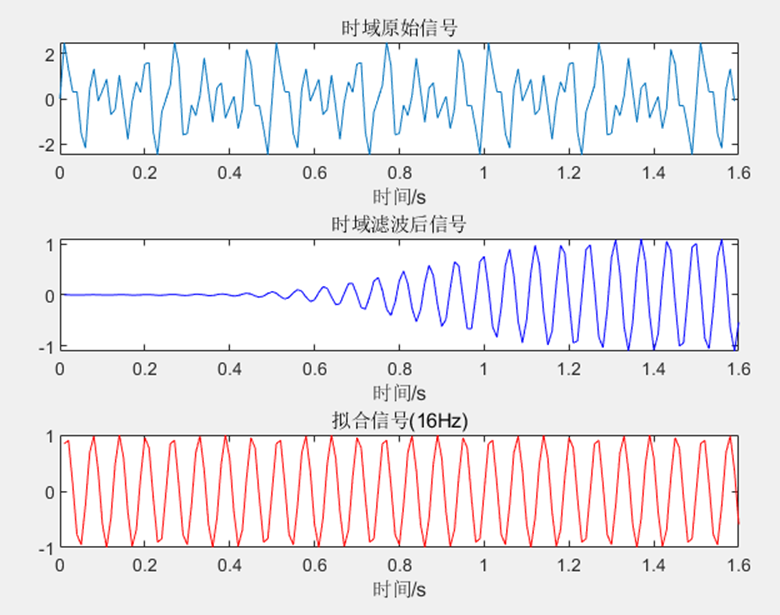
（2）16Hz带通滤波器

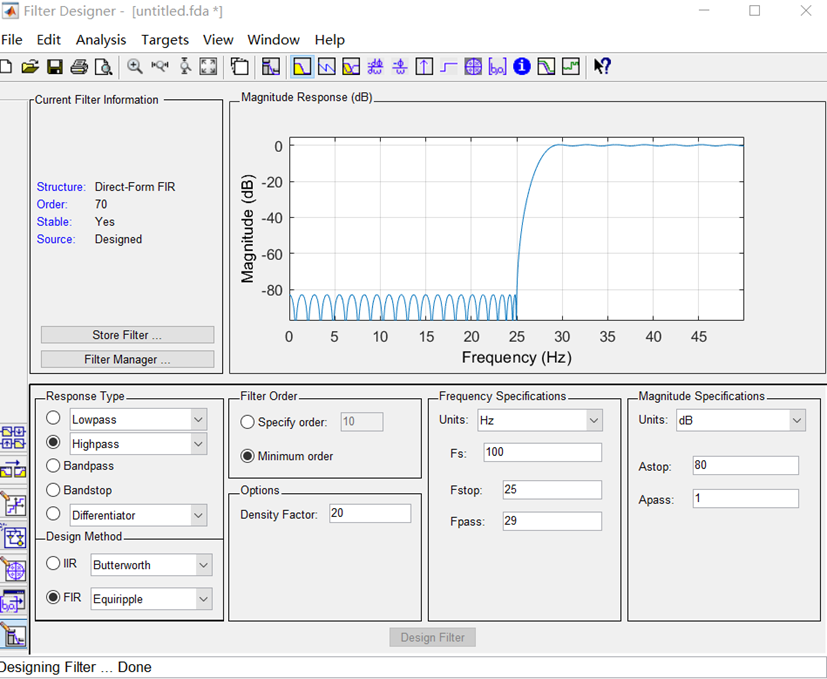
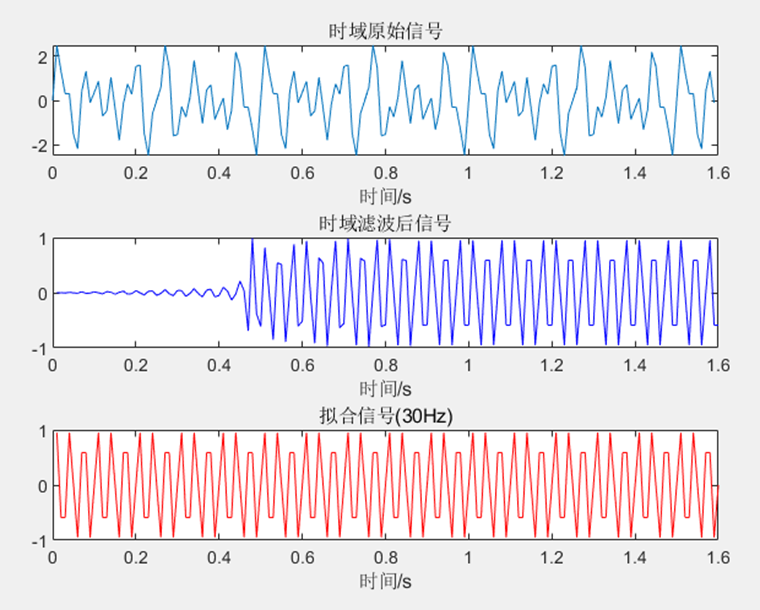
（3）30Hz高通滤波器

通过分析发现信号滤波之后相位会发生一定的滞后。

4. 将滤得的频率成分叠加生产原信号，并与给的标准原信号进行对比

%4.将滤得的频率成分叠加生产原信号，并与给的标准原信号进行对比。
clear all;
load('E:\MATLAB\zibiancx\yy59');
Fs = 100;  % 原始信号采样频率,  100Hz
Ts = 1/Fs; % 原始信号采样周期,  0.01s
L = 160;   % 使用原始序列个数
for i=1:L
    z(i)=yy9(i);
    t(i)=i/100;
end
figure(9);
output1 = filter(filter12, z);
output2 = filter(filter16, z);
output3 = filter(filter30, z);
subplot(511);
plot(t,output1);title('滤波信号(12Hz)'),xlabel('时间/s');
subplot(512);
plot(t,output2, 'b');title('滤波信号(16Hz)'),xlabel('时间/s');
subplot(513);
plot(t,output3, 'g');title('滤波信号(30Hz)'),xlabel('时间/s');
subplot(514);
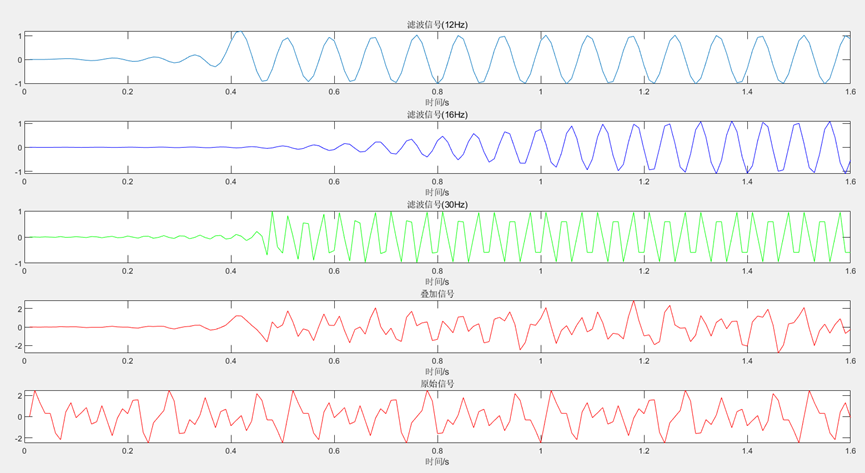
plot(t,output1+output2+output3, 'r');title('叠加信号'),xlabel('时间/s');
subplot(515);
plot(t,z, 'r');title('原始信号'),xlabel('时间/s');

分析可知，从0.8s开始，叠加信号开始稳定，并且呈现出周期性，周期与原始信号一致，但是图像形状与原始信号有差距。可能是因为滤波器参数设置问题，也可能是因为滤波过程中有损失等

下图则为程序运行的全数据：