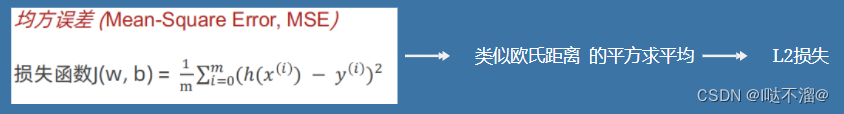目录
目录
前言
前言
机器学习中的线性回归方程算法是一种基础的预测性建模技术,它研究的是因变量(目标变量)与自变量(特征变量)之间的关系。线性回归试图找到一条最佳的直线(在多维空间中可能是超平面),这条直线能够尽可能地拟合数据点,从而能够预测新的数据点的目标值。
在接下来的内容中,我们将详细介绍线性回归方程算法的原理、实现步骤以及其在实践中的应用,并如何去优化对应的参数找到问题的最优解。通过对这些内容的了解,读者将能够掌握线性回归方程算法的基本知识和技能,为进一步学习和应用机器学习算法打下坚实的基础。
文章介绍内容由浅入深,内容非常丰富,适合初学者进行学习。
一、线性回归算法的概述
1. 定义
2. 特点
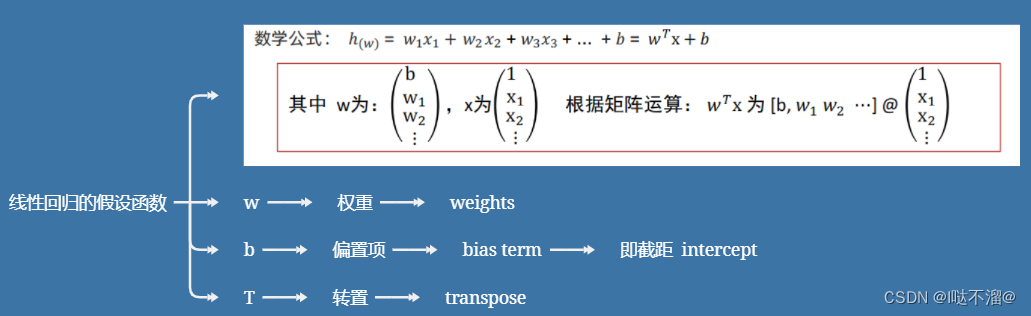
3. 假设函数
4. 举个栗子
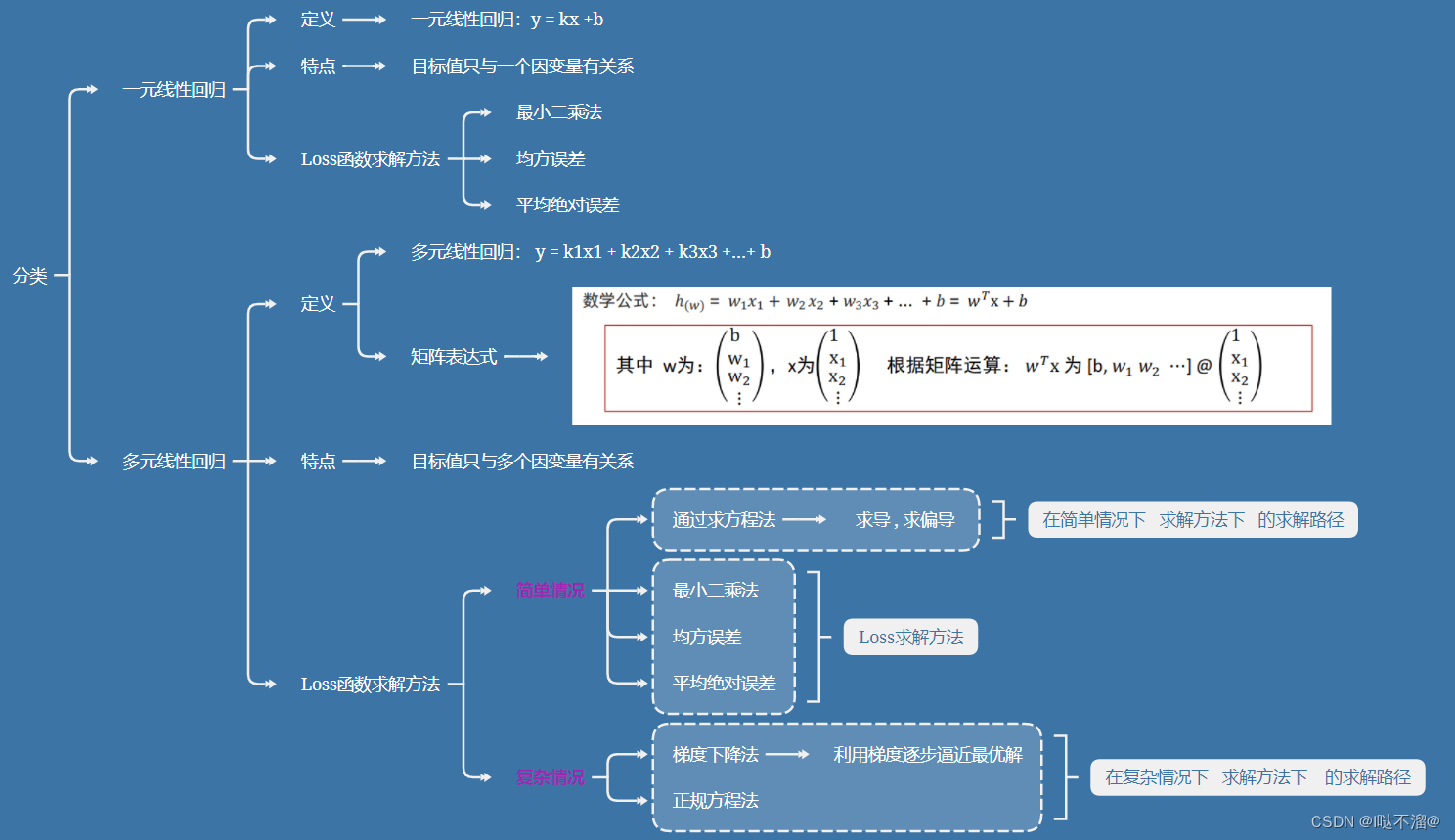
5. 分类
6. 应用场景
二、损失函数
1. 定义
2. 作用
3. 误差和最优解
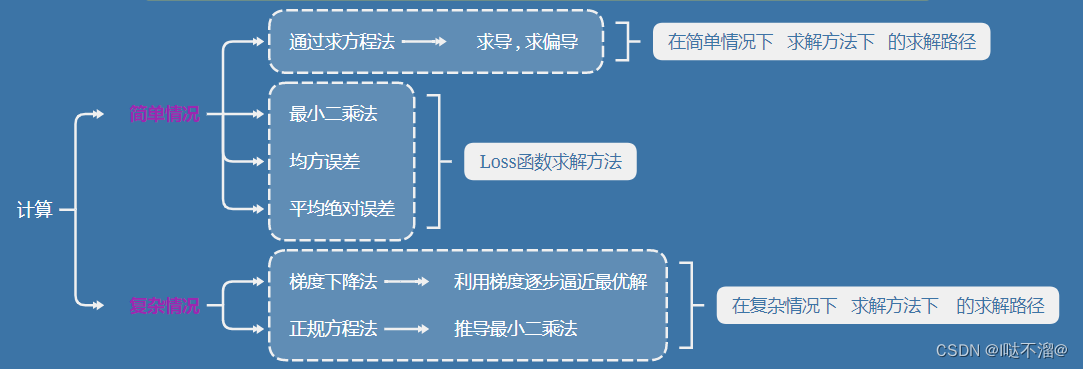
4. 计算
5. 最小二乘误差
6. 均方误差(MSE)
7. 平均绝对误差(MAE)
8. 引入损失函数
三、正规方程法
1. 定义
2. 应用场景
3. 特点
4. 表达式
5. 最优解
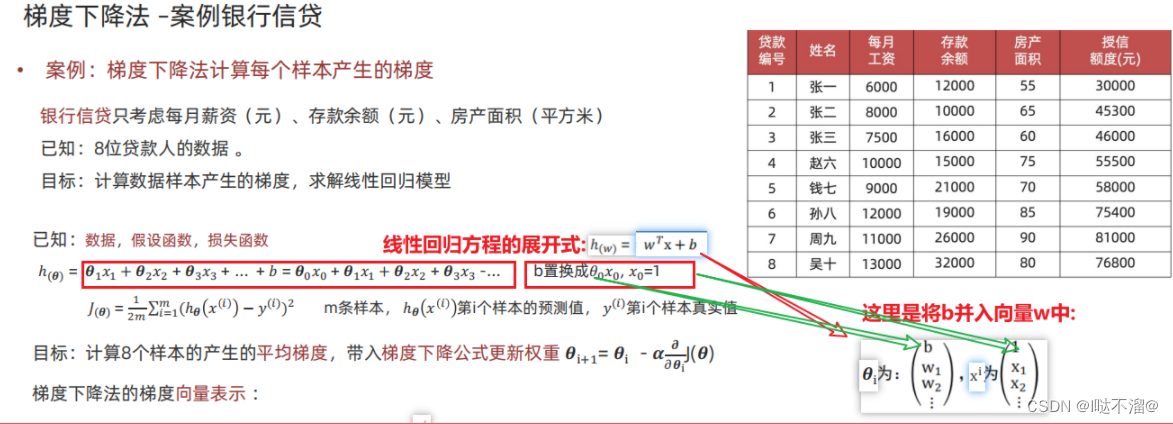
四、梯度下降法(核心)
1. 定义
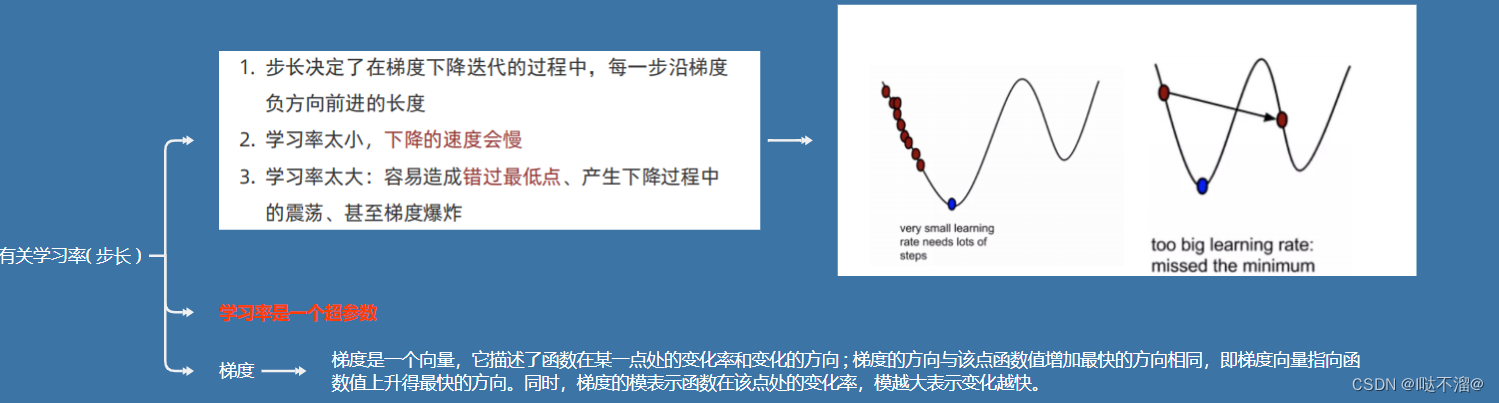
2. 梯度
3. 应用场景
4. 特点
5. 梯度下降过程
5.1 概述
5.2 基本公式
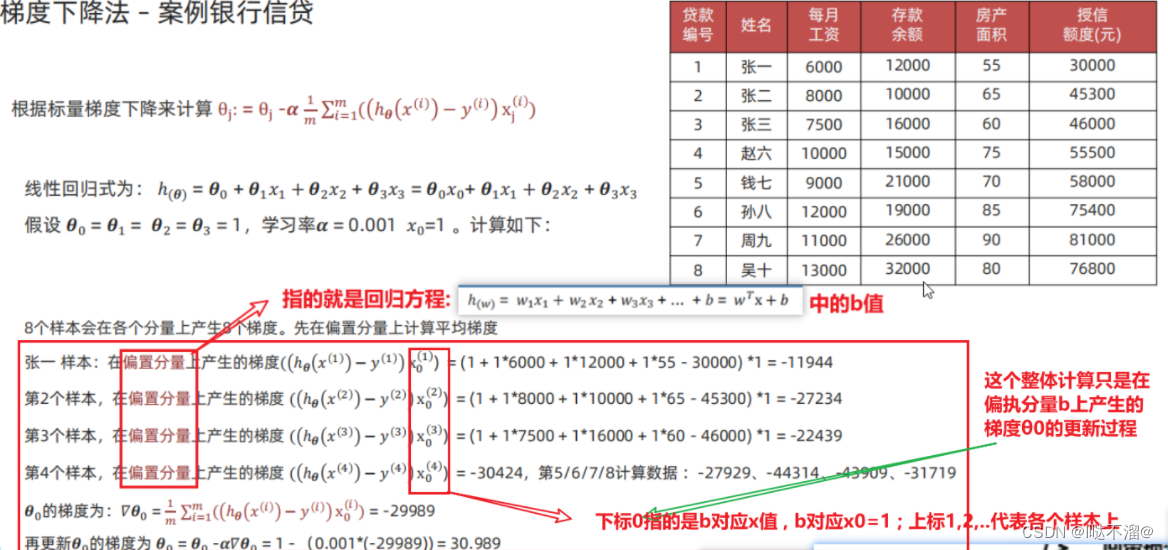
5.3 结合案例推导梯度下降法的标量表示
5.4 有关学习率α
5.5 梯度下降法的过程
5.6 梯度下降法的分类
- 全梯度下降算法 (FGD)
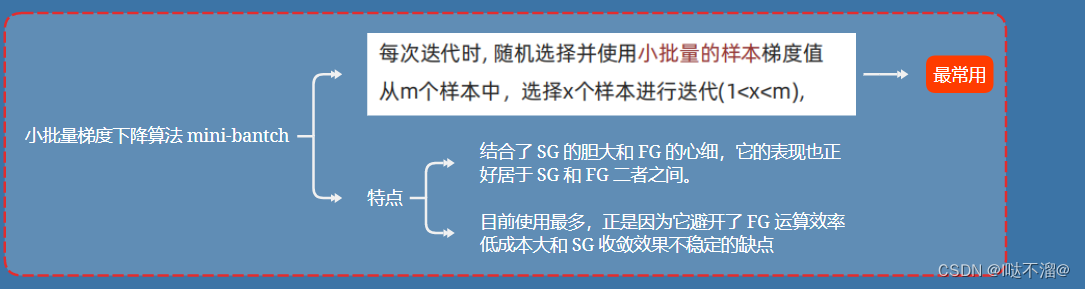
- 小批量梯度下降算法 (mini-bantch)
- 随机平均梯度下降算法(SAG)
- 随机梯度下降算法(SGD)
5.7 过程举例
- 单变量梯度下降
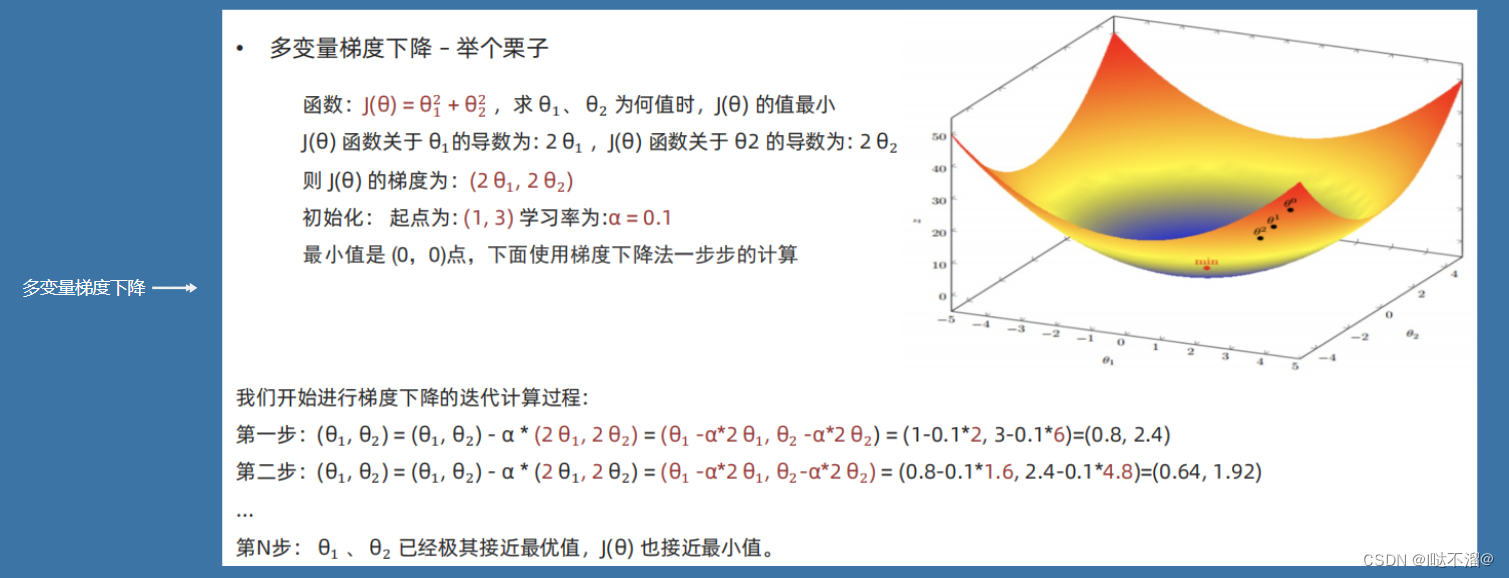
- 多变量梯度下降
五、回归模型评估方法
1. 导包
2. 为什么要评估?
3. 评估分类
3.1 MAE
3.2 MSE
3.3 RMSE
4.对比
六、线性回归方程的API
1. 正规方程API
2. 梯度下降法API
七、欠拟合和过拟合
1. 过拟合
2. 欠拟合
3. 泛化
八、正则化
1. 定义
2. L1正则化
3. L2正则化
4. 注意的点
九、数学基础
1. 标量与向量
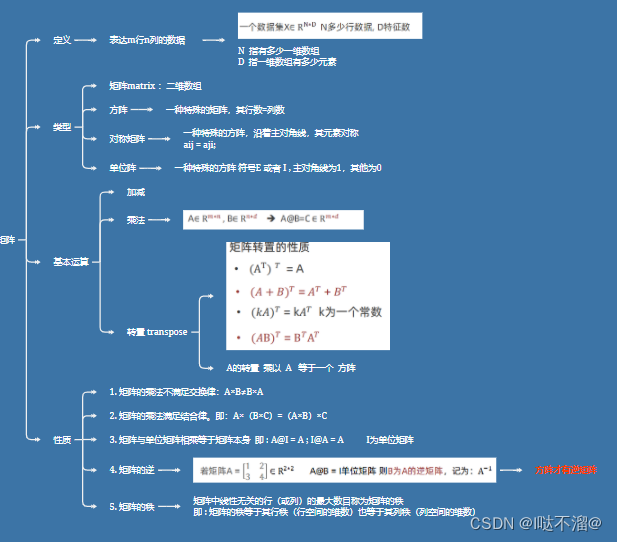
2. 矩阵
3. 张量
4. 导数
十、总结
线性回归方程算法是一种基础且重要的机器学习技术,具有广泛的应用场景和实用价值。通过深入理解其基本原理、关键步骤和注意事项,我们可以更好地应用该算法来解决实际问题。同时,随着技术的不断发展和创新,线性回归方程算法也将不断得到优化和改进,为机器学习领域的发展贡献更多的力量。