在上一篇中,我们讨论了集成学习中的Bagging方法,在本文中,我们将继续深入研究集成学习,学习Boosting方法
一. Boosting思想
在对Bagging思想中随机森林算法有了一定了解之后,我们会发现
在随机森林构建过程中,各棵树之间是相对独立的
也就是说:在构建第m棵子树的时候,不会考虑前面的m-1棵树
那么,我们能否对这个现象进行优化呢?
- 在构建第m棵子树的时候,考虑到前m-1棵子树的结果,会不会对最终
结果产生有益的影响? - 各个决策树组成随机森林后,最终结果能否存在一种既定的决策顺序,即哪颗子树先进行决策、哪颗子树后进行决策
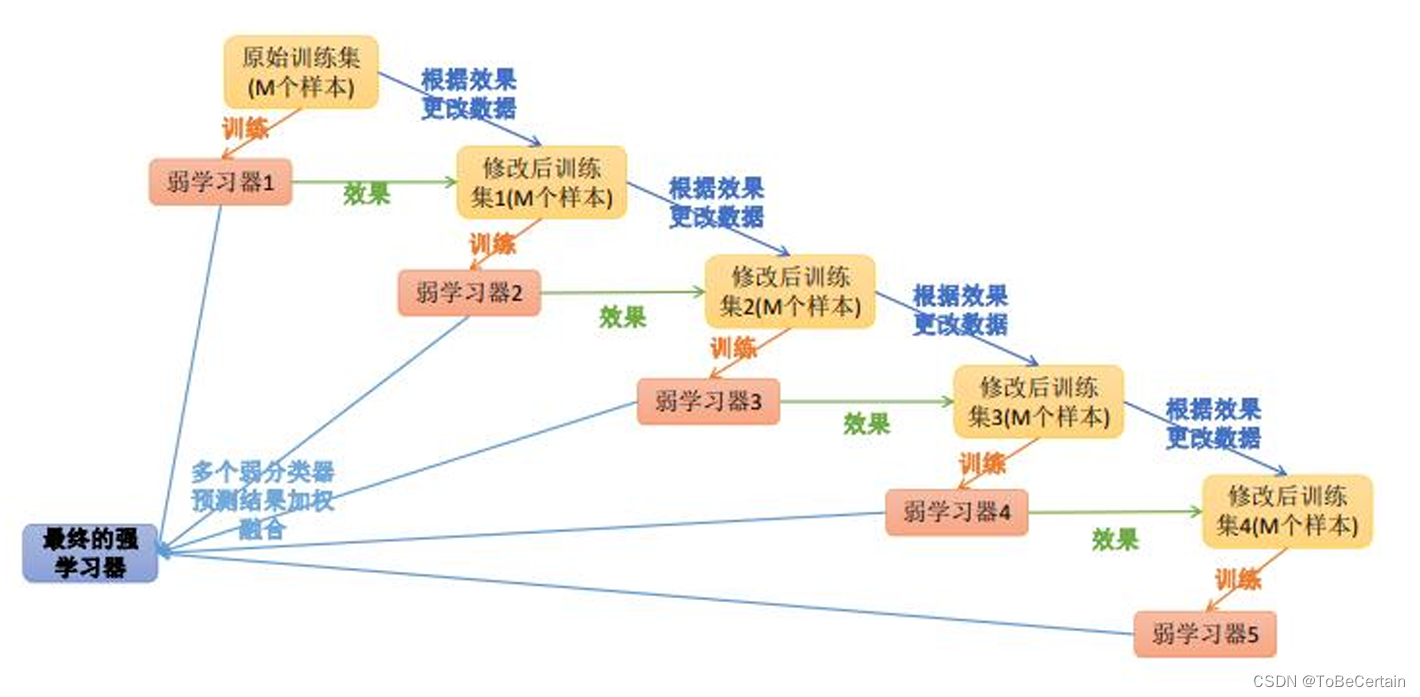
针对上面提出的优化方向,集成学习又提出了提升学习(Boosting)思想
思想:
在弱学习器A的基础上训练得到弱学习器B
弱学习器B+弱学习器A的预测结果一定优于弱学习器A
即:每一步产生的弱预测模型加权累加到总模型中
boosting意义:
弱预测模型可以通过提升技术得到一个强预测模型
boosting思想:
可以用于回归和分类的问题
1. Adaboost 算法
Adaptive Boosting是一种迭代算法,即将基学习器的线性组合作为强学习器
既可以用于分类问题,也可以用于回归问题
AdaBoost算法主要用于解决分类问题,基学习器是CART分类树
AdaBoost算法也可以用于解决回归问题,基学习器是CART回归树,这种变体被称为AdaBoost.R2
具体操作:
1. 训练数据集,产生一个新的弱学习器
2. 使用该学习器对所有训练样本进行预测
3. 评估每个样本的重要性,即为每个样本赋予一个权重
如果某个样本点被预测的越正确,则将样本权重降低
如果某个样本点被预测的越错误,则将样本权重提高,即,越难区分的样本在下一次迭代中会变得越重要
注意:这里样本的权重是归一的
4. 通过迭代,得到n个基学习器
对于误差率较小的基学习器以大的权重值
对于误差率较大的基学习器以小的权重值
注意:这里基学习器的权重不归一
5. 线性组合所有基学习器
停止条件:
错误率足够小或者达到一定的迭代次数
以二分类任务为例子,Adaboost 将基分类器的线性组合作为强分类器,即
f
(
x
)
=
∑
m
=
1
M
α
m
G
m
(
x
)
f(x) = \sum_{m=1}^{M}\alpha_{m}G_{m}(x)
f(x)=m=1∑MαmGm(x)
公式解释:
G m ( x ) G_{m}(x) Gm(x)为基分类器,且 G m ( x ) = ± 1 G_{m}(x)=\pm1 Gm(x)=±1
α m \alpha_{m} αm为基分类器对应的权重,且 α m > 0 \alpha_{m}>0 αm>0,不归一
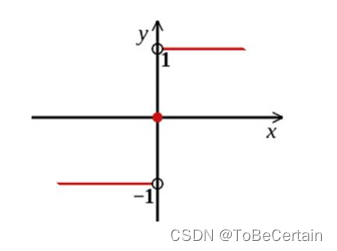
最终分类器是在线性组合的基础上进行Sign函数转换,因此最终的强学习器为:
G
(
x
)
=
s
i
g
n
[
f
(
x
)
]
=
s
i
g
n
[
∑
m
=
1
M
α
m
G
m
(
x
)
]
G(x) = sign[f(x)] = sign[\sum_{m=1}^{M}\alpha_{m}G_{m}(x)]
G(x)=sign[f(x)]=sign[m=1∑MαmGm(x)]
公式解释:
当所有样本的加权和为正数时,输出 G ( x ) = 1 G(x)=1 G(x)=1
当所有样本的加权和为负数时,输出 G ( x ) = − 1 G(x)=-1 G(x)=−1
当所有样本的加权和为0时,返回任意值
根据上面的公式,我们用错误率构建损失函数,就会得到每个学习器的损失函数,即分错了的样本权重和:
l
o
s
s
=
∑
i
=
1
n
w
i
I
[
G
(
x
i
)
≠
y
i
]
,
I
(
b
)
=
{
1
,
b
=
T
r
u
e
0
,
b
=
F
a
l
s
e
,
∑
i
=
1
n
w
i
=
1
loss = \sum_{i=1}^{n}w_{i}I[G(x_{i})\ne y_{i}] ,I(b)=\left\{\begin{matrix}1,b=True \\0,b=False\end{matrix}\right.,\sum_{i=1}^{n} w_{i}=1{\tiny }
loss=i=1∑nwiI[G(xi)=yi],I(b)={1,b=True0,b=False,i=1∑nwi=1
公式解释:
x i , y i x_{i},y_{i} xi,yi分别为训练集的特征值和标签值
∑ i = 1 n \sum_{i=1}^{n} ∑i=1n表示训练集中有n个样本
w i w_{i} wi为每个样本的权重,归一
G ( x i ) G(x_{i}) G(xi)为基学习器的预测值,即输入x值,输出+1 / -1
I [ G ( x i ) ≠ y i ] I[G(x_{i})\ne y_{i}] I[G(xi)=yi]表示当预测错误时, I 函数 I函数 I函数返回1
公式说明:
训练样本固定,但每个样本的权重不同,因此 G ( ) G( ) G()不同
这里,由于损失函数是分段函数,不方便求导,所以我们可以通过边界值来求导,即损失函数(上界)公式为:
l
o
s
s
=
∑
i
=
1
n
w
i
I
[
G
(
x
i
)
≠
y
i
]
≤
∑
i
=
1
n
w
i
e
(
−
y
i
f
(
x
)
)
loss = \sum_{i=1}^{n}w_{i}I[G(x_{i})\ne y_{i}] \le \sum_{i=1}^{n}w_{i}e^{(-y_{i}f(x))}
loss=i=1∑nwiI[G(xi)=yi]≤i=1∑nwie(−yif(x))
公式解释:
当 G ( x i ) ≠ y i G(x_{i})\ne y_{i} G(xi)=yi, I 函数 = 1 I函数=1 I函数=1,此时 f ( x ) < 0 , y i = 1 f(x)<0,y_{i} =1 f(x)<0,yi=1,即 e x > 1 e^{x}>1 ex>1
当 G ( x i ) = y i G(x_{i})= y_{i} G(xi)=yi, I 函数 = 0 I函数=0 I函数=0,此时 f ( x ) > 0 , y i = 1 f(x)>0,y_{i} =1 f(x)>0,yi=1,即 e x > 0 e^{x}>0 ex>0
现在假设我们已经得到了第
k
−
1
k-1
k−1轮的强学习器:
f
k
−
1
(
x
)
=
∑
j
=
1
k
−
1
α
j
G
j
(
x
)
f_{k-1}(x)=\sum_{j=1}^{k-1}\alpha _{j}G_{j} (x)
fk−1(x)=j=1∑k−1αjGj(x)
那么,对于第
k
k
k轮的强化学习器,可以写为:
f
k
(
x
)
=
f
k
−
1
(
x
)
+
α
k
G
k
(
x
)
=
∑
j
=
1
k
α
j
G
j
(
x
)
f_{k}(x)=f_{k-1}(x)+\alpha _{k}G_{k}(x)=\sum_{j=1}^{k}\alpha _{j}G_{j} (x)
fk(x)=fk−1(x)+αkGk(x)=j=1∑kαjGj(x)
因此对于第m次迭代,损失函数为:
l
o
s
s
(
α
m
,
G
m
(
x
)
)
=
∑
i
=
1
n
w
m
−
1
,
i
e
−
(
y
i
f
m
(
x
)
)
loss(\alpha _{m},G_{m}(x)) = \sum_{i=1}^{n}w_{m-1,i}e^{-(y_{i}f_{m}(x))}
loss(αm,Gm(x))=i=1∑nwm−1,ie−(yifm(x))
公式解释:
w m − 1 , i w_{m-1,i} wm−1,i为第m-1轮中,每个样本的权重值
f m ( x ) f_{m}(x) fm(x)为第m轮传入的样本
注意:这里第m-1轮次的参数是已知的
公式推导:= ∑ i = 1 n w m − 1 , i e − ( y i ( f m − 1 ( x ) + α m G m ( x ) ) ) =\sum_{i=1}^{n}w_{m-1,i}e^{-(y_{i}(f_{m-1}(x)+\alpha _{m}G_{m}(x)))} =∑i=1nwm−1,ie−(yi(fm−1(x)+αmGm(x)))
= ∑ i = 1 n w m − 1 , i e − y i ( f m − 1 ( x ) ) e − y i ( α m G m ( x ) ) =\sum_{i=1}^{n}w_{m-1,i}e^{-y_{i}(f_{m-1}(x))}e^{-y_{i}(\alpha _{m}G_{m}(x))} =∑i=1nwm−1,ie−yi(fm−1(x))e−yi(αmGm(x))
= ∑ i = 1 n w m , i e − y i ( α m G m ( x ) ) =\sum_{i=1}^{n}w_{m,i}e^{-y_{i}(\alpha _{m}G_{m}(x))} =∑i=1nwm,ie−yi(αmGm(x))
其中, w m , i = w m − 1 , i e − y i ( f m − 1 ( x ) ) w_{m,i}=w_{m-1,i}e^{-y_{i}(f_{m-1}(x))} wm,i=wm−1,ie−yi(fm−1(x))
此时每个样本的权重值不归一,即 w m , i w_{m,i} wm,i不归一对 w m − 1 , i w_{m-1,i} wm−1,i除以一个常数,做归一化操作:
∑ i = i m w ˉ m , i = 1 \sum_{i=i}^{m} \bar{w}_{m,i}=1 i=i∑mwˉm,i=1
最终的损失函数公式为:
l
o
s
s
(
a
m
,
G
m
(
x
)
)
=
∑
i
=
1
n
w
ˉ
m
,
i
e
−
y
i
(
α
m
G
m
(
x
)
)
loss(a_{m},G_{m}(x))=\sum_{i=1}^{n}\bar{w} _{m,i}e^{-y_{i}(\alpha _{m}G_{m}(x))}
loss(am,Gm(x))=i=1∑nwˉm,ie−yi(αmGm(x))
那么,使损失函数达到最小值的 α m α_{m} αm和 G m G_{m} Gm就是AdaBoost算法的第m个学习器的最终解;
因此,最佳的第m个学习器
G
m
G_{m}
Gm公式为:
G
m
∗
(
x
)
=
min
G
m
(
x
)
∑
i
=
1
n
w
ˉ
m
,
i
I
(
y
i
≠
G
m
(
x
i
)
)
G_{m}^{*} (x)=\min_{G_{m}(x)}\sum_{i=1}^{n}\bar{w} _{m,i}I(y_{i}\ne G_{m}(x_{i}))
Gm∗(x)=Gm(x)mini=1∑nwˉm,iI(yi=Gm(xi))
公式解释:
该公式表示:使得样本权重在 w m , i w_{m,i} wm,i条件下,被分错的数量尽量的少
此时,误差为:
ϵ
m
=
∑
y
i
≠
G
m
(
x
)
w
ˉ
m
,
i
\epsilon _{m}=\sum_{y_{i}\ne G_{m}(x)} \bar{w}_{m,i}
ϵm=yi=Gm(x)∑wˉm,i
公式解释:
这里我们梳理一下求解逻辑:
- 首先通过前 m − 1 m-1 m−1轮求出第 m m m轮的权重 w m , i w_{m,i} wm,i
- 得到权重 w m , i w_{m,i} wm,i后,通过最小化分错的数量,更新第m个学习器 G m ∗ G_{m}^{*} Gm∗
- 此时,也就得到了第m个学习器下分错样本的权重和,即 ϵ m \epsilon_{m} ϵm
在得到
G
m
∗
和
ϵ
m
G_{m}^{*}和\epsilon_{m}
Gm∗和ϵm后,我们就会相应的得到第m轮学习器的权重
α
m
∗
\alpha _{m}^{*}
αm∗,即:
α
m
∗
=
1
2
l
n
(
1
−
ϵ
m
ϵ
m
)
\alpha _{m}^{*} =\frac{1}{2}ln( \frac{1-\epsilon _{m}}{\epsilon _{m}} )
αm∗=21ln(ϵm1−ϵm)
公式推导:
此时, G m ( x ) G_{m}(x) Gm(x)已知
l o s s ( a m , G m ( x ) ) loss(a_{m},G_{m}(x)) loss(am,Gm(x))
= ∑ i = 1 n w ˉ m , i e − y i ( α m G m ( x ) ) =\sum_{i=1}^{n}\bar{w} _{m,i}e^{-y_{i}(\alpha _{m}G_{m}(x))} =∑i=1nwˉm,ie−yi(αmGm(x))
= ∑ y = G ( x ) w ˉ m , i e − α m + ∑ y ≠ G ( x ) w ˉ m , i e α m =\sum_{y = G(x)}\bar{w}_{m,i}e^{-\alpha _{m}} +\sum_{y\ne G(x)} \bar{w}_{m,i}e^{\alpha _{m}} =∑y=G(x)wˉm,ie−αm+∑y=G(x)wˉm,ieαm
= ∑ y = G ( x ) w ˉ m , i e − α m + ϵ m e α m =\sum_{y = G(x)}\bar{w}_{m,i}e^{-\alpha _{m}} +\epsilon _{m}e^{\alpha _{m}} =∑y=G(x)wˉm,ie−αm+ϵmeαm
= ∑ y = G ( x ) w ˉ m , i e − α m + ϵ m e α m + ∑ y ≠ G ( x ) w ˉ m , i e − α m − ∑ y ≠ G ( x ) w ˉ m , i e − α m =\sum_{y = G(x)}\bar{w}_{m,i}e^{-\alpha _{m}} +\epsilon _{m}e^{\alpha _{m}}+\sum_{y\ne G(x)} \bar{w}_{m,i}e^{-\alpha _{m}}-\sum_{y\ne G(x)} \bar{w}_{m,i}e^{-\alpha _{m}} =∑y=G(x)wˉm,ie−αm+ϵmeαm+∑y=G(x)wˉm,ie−αm−∑y=G(x)wˉm,ie−αm
= ∑ i = 1 n w ˉ m , i e − α m + ϵ m e α m − ϵ m e − α m =\sum_{i=1}^{n} \bar{w}_{m,i}e^{-\alpha _{m}} +\epsilon _{m}e^{\alpha _{m}}-\epsilon _{m}e^{-\alpha _{m}} =∑i=1nwˉm,ie−αm+ϵmeαm−ϵme−αm
= e − α m + ϵ m e α m − ϵ m e − α m =e^{-\alpha _{m} }+\epsilon _{m}e^{\alpha _{m}}-\epsilon _{m}e^{-\alpha _{m}} =e−αm+ϵmeαm−ϵme−αm
通过对损失函数求导,即可得到 α m ∗ \alpha _{m}^{*} αm∗
d l o s s d α m = − e − α m + ϵ m e α m + ϵ m e − α m = 0 \frac{\mathrm{d} loss}{\mathrm{d} \alpha _{m}} =-e^{-\alpha _{m} }+\epsilon _{m}e^{\alpha _{m}}+\epsilon _{m}e^{-\alpha _{m}}=0 dαmdloss=−e−αm+ϵmeαm+ϵme−αm=0
⟹ ( ϵ m − 1 ) e − α m + ϵ m e α m = 0 \Longrightarrow (\epsilon _{m}-1)e^{-\alpha _{m} }+\epsilon _{m}e^{\alpha _{m}}=0 ⟹(ϵm−1)e−αm+ϵmeαm=0
⟹ ( 1 − ϵ m ) e − α m = ϵ m e α m \Longrightarrow(1-\epsilon _{m})e^{-\alpha _{m} }=\epsilon _{m}e^{\alpha _{m}} ⟹(1−ϵm)e−αm=ϵmeαm
⟹ e α m e − α m = ( 1 − ϵ m ) ϵ m \Longrightarrow \frac{e^{\alpha _{m}}}{e^{-\alpha _{m} }} =\frac{(1-\epsilon _{m})}{\epsilon _{m}} ⟹e−αmeαm=ϵm(1−ϵm)
⟹ e 2 a m = ( 1 − ϵ m ) ϵ m \Longrightarrow e^{2a_{m}} =\frac{(1-\epsilon _{m})}{\epsilon _{m}} ⟹e2am=ϵm(1−ϵm)
⟹ l n e 2 a m = l n [ ( 1 − ϵ m ) ϵ m ] \Longrightarrow lne^{2a_{m}} =ln[\frac{(1-\epsilon _{m})}{\epsilon _{m}}] ⟹lne2am=ln[ϵm(1−ϵm)]
⟹ a m = 1 2 l n [ ( 1 − ϵ m ) ϵ m ] \Longrightarrow a_{m} =\frac{1}{2} ln[\frac{(1-\epsilon _{m})}{\epsilon _{m}}] ⟹am=21ln[ϵm(1−ϵm)]
1.1 Adaboost算法构建流程
- 存在训练数据集 X = ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . . ( x n , y n ) X={(x1 ,y1 ),(x2 ,y2 )....(xn,yn)} X=(x1,y1),(x2,y2)....(xn,yn)
- 初始化每个样本的权重 D 1 = ( w 11 , w 12 , w 13 , . . . , w 1 n ) , w 1 i = 1 n ( i = 1 , 2 , 3... , n ) D_{1}=(w_{11},w_{12},w_{13},...,w_{1n}),w_{1i}=\frac{1}{n}(i=1,2,3...,n) D1=(w11,w12,w13,...,w1n),w1i=n1(i=1,2,3...,n)
- 使用具有权值分布D1的训练数据集学习,得到基分类器
G
1
(
x
)
G_{1}(x)
G1(x)
注意:这里得到的是每个样本的预测值,即:+1或-1 - 根据预测值,计算 G 1 ( x ) G_{1}(x) G1(x)在训练集上的分类误差: ε 1 = P ( G 1 ≠ y ) = ∑ i = 1 n w ˉ m i I ( y i ≠ G m ( x i ) ) = ∑ y i ≠ G m ( x i ) w ˉ m i \varepsilon _{1}=P(G_{1}\ne y)=\sum_{i=1}^{n}\bar{w}_{mi}I(y_{i}\ne G_{m}(x_{i}))=\sum_{y_{i}\ne G_{m}(x_{i})}\bar{w}_{mi} ε1=P(G1=y)=i=1∑nwˉmiI(yi=Gm(xi))=yi=Gm(xi)∑wˉmi
- 计算
G
1
(
x
)
G_{1}(x)
G1(x)模型的权重系数
α
1
α_{1}
α1
α 1 = 1 2 l n [ ( 1 − ϵ m ) ϵ m ] α_{1}=\frac{1}{2} ln[\frac{(1-\epsilon _{m})}{\epsilon _{m}}] α1=21ln[ϵm(1−ϵm)] - 构建线性组合:
f ( x ) = ∑ m = 1 M α m G m ( x ) f(x)=\sum_{m=1}^{M} \alpha _{m}G_{m}(x) f(x)=m=1∑MαmGm(x) - 更新训练数据集中每个样本的权值分布,用来训练下一个基分类器
D 2 = ( w 21 , w 22 , w 23 , . . . , w 2 n ) D_{2}=(w_{21},w_{22},w_{23},...,w_{2n}) D2=(w21,w22,w23,...,w2n)
w 2 i = w 1 i e − y i α 1 G 1 ( x i ) w_{2i}=w_{1i}e^{-y_{i}\alpha _{1}G_{1}(x_{i})} w2i=w1ie−yiα1G1(xi)
参数解释:
G 1 ( x i ) G_{1}(x_{i}) G1(xi)为上一个弱学习器的预测值,对应第3步
归一化:
w
m
+
1
,
i
=
w
m
,
i
Z
m
e
−
y
i
α
m
G
m
(
x
i
)
归一化:w_{m+1,i}=\frac{w_{m,i}}{Z_{m}}e^{-y_{i}\alpha _{m}G_{m}(x_{i})}
归一化:wm+1,i=Zmwm,ie−yiαmGm(xi)
其中,
Z
m
=
∑
i
=
1
M
w
m
,
i
e
−
y
i
α
m
G
m
(
x
i
)
其中,Z_{m}=\sum_{i=1}^{M}w_{m,i}e^{ -y_{i}\alpha _{m}G_{m}(x_{i})}
其中,Zm=i=1∑Mwm,ie−yiαmGm(xi)
8. 重复上述操作
9. 得到最终的分类器
G
(
x
)
=
s
i
g
n
[
f
(
x
)
]
=
s
i
g
n
[
∑
m
=
1
M
α
m
G
m
(
x
)
]
G(x) = sign[f(x)] = sign[\sum_{m=1}^{M}\alpha_{m}G_{m}(x)]
G(x)=sign[f(x)]=sign[m=1∑MαmGm(x)]
1.2 sklearn库参数说明
对于sklearn.ensemble.AdaBoostClassifier或 sklearn.ensemble.AdaBoostRegressor:
学习器:默认为CART分类树/ CART回归树
最大迭代次数:值过小可能会导致欠拟合,值过大可能会导致过拟合,一般50~100比较适合,默认50
学习率:调节学习速率,可以防止过拟合
2. Gradient Boosting 算法
Gradient Boosting,即梯度提升迭代决策树Gradient Boosting Decison Tree,与AdaBoost类似,也是加法模型;
AdaBoost算法:
根据前一轮弱学习器的误差来更新样本权重值,然后进行迭代
GBDT算法:
根据前一轮的弱学习器的误差来重新计算目标值,然后进行迭代
GBDT算法既可以用于解决分类问题,也可以用于解决回归问题
GBDT算法的基学习器是CART回归树
2.1 Gradient Boosting算法构建流程
目标是找到使损失函数L(Y,F(X))的损失值最小的近似函数F(X)
F ( x ) = arg min c L ( y i , F ( x ) ) F(x) = \arg\min_{c}L(y_{i},F(x)) F(x)=argcminL(yi,F(x))
以回归任务为例子:
- 存在训练数据集 X = ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . . ( x n , y n ) X={(x1 ,y1 ),(x2 ,y2 )....(xn,yn)} X=(x1,y1),(x2,y2)....(xn,yn)
- 给定第一个常数函数 f 0 f_{0} f0,即: f 0 ( x ) = c f_{0}(x) = c f0(x)=c
对于回归任务:
定义损失函数 L ( y , F ( x ) ) = 1 2 ( y − F ( x ) ) 2 L(y,F(x)) = \frac{1}{2}(y-F(x))^{2} L(y,F(x))=21(y−F(x))2
- 在给定的常数函数的基础上,求损失最小:
f 0 ( x ) = c = a r g min c ∑ i = 1 n L ( y i , F ( x ) ) = a r g min c ∑ i = 1 n 1 2 ( y i − c ) 2 f_{0}(x) = c=arg\min_{c} \sum_{i=1}^{n}L(y_{i},F(x))=arg\min_{c} \sum_{i=1}^{n}\frac{1}{2}(y_{i}-c)^{2} f0(x)=c=argcmini=1∑nL(yi,F(x))=argcmini=1∑n21(yi−c)2
在回归任务中,损失最小时,函数的预测值为:均值
即:c一般选择平均值
也就是说:所有Y值取平均
-
构造第1棵树:
计算每一个样本损失函数的负梯度值:
对于初始化常数函数,负梯度值为c对于第1棵树,第2棵树,… ,:
y i m = − ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) y_{im} = -\frac{\partial L(y_{i},F(x_{i}))}{\partial F(x_{i})} yim=−∂F(xi)∂L(yi,F(xi))
其中, F ( x ) = F m − 1 ( x ) 其中,F(x)=F_{m-1}(x) 其中,F(x)=Fm−1(x)
公式解释:
F m − 1 ( x ) F_{m-1}(x) Fm−1(x)是前 m − 1 m-1 m−1个CART树的和
F m − 1 ( x ) = ∑ j = 0 m − 1 f j ( x ) F_{m-1}(x)=\sum_{j=0}^{m-1} f_{j}(x) Fm−1(x)=j=0∑m−1fj(x)
对于第1棵树, F 2 − 1 ( x ) = f 0 ( x ) F_{2-1}(x)=f_{0}(x) F2−1(x)=f0(x)
对于第2棵树, F 3 − 1 ( x ) = f 0 ( x ) + f 1 ( x ) F_{3-1}(x)=f_{0}(x)+f_{1}(x) F3−1(x)=f0(x)+f1(x)
-
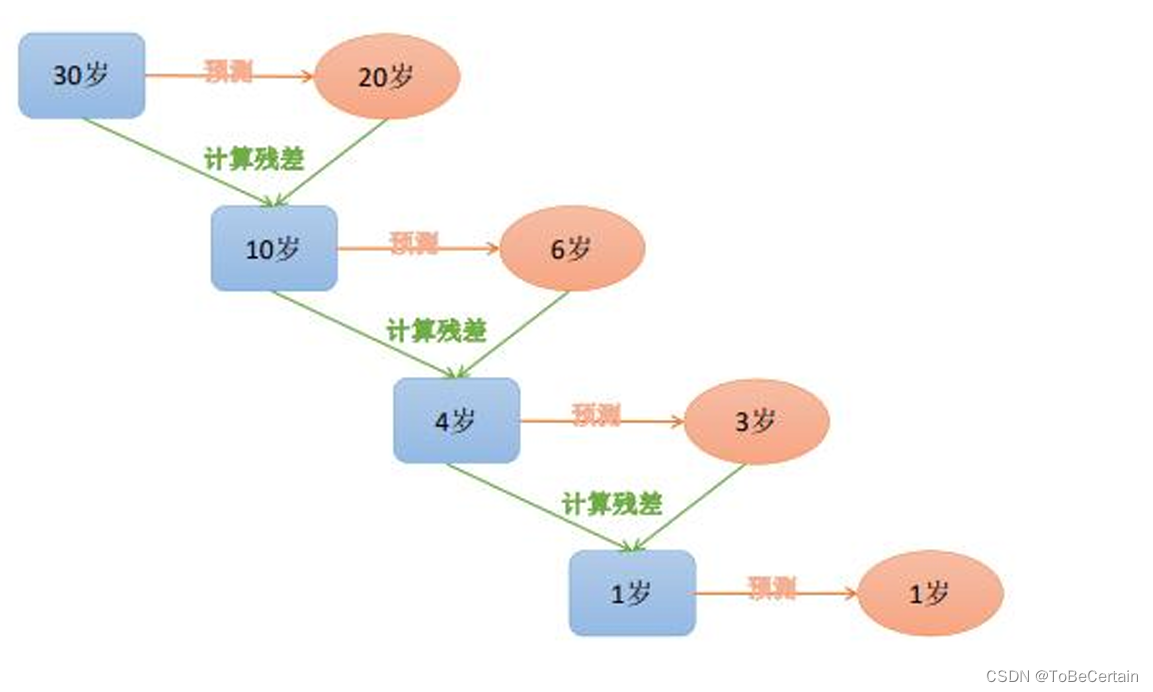
通过求解负梯度值,更新Y值:
对于最小二乘损失构造的损失函数,负梯度值就为残差:
y i m = y i − F m − 1 ( x i ) y_{im}=y_{i}-F_{m-1}(x_{i}) yim=yi−Fm−1(xi) -
更新模型
F ( x ) = ∑ i = 0 M f i ( x ) F(x)=\sum_{i=0}^{M} f_{i}(x) F(x)=i=0∑Mfi(x) -
重复第4步-第6步操作
-
为了防止每个学习器能力过强而导致过拟合,在上述的学习过程中可以给定一个学习率v:
F ( x ) = v ∑ i = 0 M f i ( x ) F(x)=v\sum_{i=0}^{M} f_{i}(x) F(x)=vi=0∑Mfi(x)v减小时,M个数变多
2.2 Gradient Boosting算法的回归与分类问题
GBDT回归算法和分类算法的唯一区别:
选择的损失函数不同,因此对应的负梯度值不同,采用的模型初值也不一样
2.2.1 Gradient Boosting回归算法
损失函数选择一般是均方差(最小二乘)和绝对值误差
均方差损失函数
- 损失函数:$L(y,F_{m}(x))=\frac{1}{2}(y-F_{m}(x))^{2} $
- 负梯度值: y i m = y i − F m − 1 ( x ) y_{im}=y_{i}-F_{m-1}(x) yim=yi−Fm−1(x)
- 初始值:一般采用均值作为初始值
绝对误差损失函数
- 损失函数: L ( y , F m ( x ) ) = ∣ y − F m ( x ) ∣ L(y,F_{m}(x))=|y-F_{m}(x)| L(y,Fm(x))=∣y−Fm(x)∣
- 负梯度值: y i m = s i g n ( y i − F m − 1 ( x ) ) y_{im}=sign(y_{i}-F_{m-1}(x)) yim=sign(yi−Fm−1(x))
- 初始值:一般采用中值作为初始值
2.2.2 Gradient Boosting分类算法
分类算法中一般选择对数损失函数来表示
对数损失函数(二分类)
- 损失函数: L ( y , F m ( x ) ) = − [ y l n ( p m ) + ( 1 − y ) l n ( 1 − p m ) ] , 其中 p m = 1 1 + e − F m ( x ) L(y,F_{m}(x))=-[yln(p_{m})+(1-y)ln(1-p_{m})],其中p_{m}=\frac{1}{1+e^{-F_{m}(x)}} L(y,Fm(x))=−[yln(pm)+(1−y)ln(1−pm)],其中pm=1+e−Fm(x)1
- 负梯度值: y i m = y i − p m y_{im}=y_{i}-p_{m} yim=yi−pm
- 初始值:一般采用 l n ( 正样本个数 / 负样本个数 ) ln(正样本个数/负样本个数) ln(正样本个数/负样本个数)作为初始值
对数损失函数(多分类)
- 损失函数: L ( y , F m l ( x ) ) = − ∑ k = 1 K y k l n p k ( x ) , 其中 p k ( x ) = e f k ( x ) ∑ l = 1 K e f l ( x ) L(y,F_{ml}(x))=-\sum_{k=1}^{K}y_{k}lnp_{k} (x),其中p_{k}(x)=\frac{e^{f_{k}(x)}}{\sum_{l=1}^{K}e^{f_{l}(x)} } L(y,Fml(x))=−∑k=1Kyklnpk(x),其中pk(x)=∑l=1Kefl(x)efk(x)
- 负梯度值: y i m l = y i l − p m l ( x ) y_{iml}=y_{il}-p_{ml}(x) yiml=yil−pml(x)
- 初始值:一般采用0作初始值
2.3 sklearn库参数说明
对于sklearn.ensemble.GradientBoostingClassifier或 sklearn.ensemble.GradientBoostingRegressor:
loss:
分类:对数似然函数deviance / 指数损失函数exponential;
默认为deviance;不建议修改
回归:均方差ls / 绝对损失lad / Huber损失 huber / 分位数损失quantile
默认ls;一般采用默认
如果噪音数据比较多,推荐huber
如果是分段预测,推荐 quantile
最大迭代次数:值过小可能会导致欠拟合,值过大可能会导致过拟合,一般50~100比较适合,默认50
学习率:默认为1;一般从一个比较小的值开始进行调参;该值越小表示需要更多的弱分类器
subsample:不放回采样
默认为1,表示不采用子采样;
小于1时,表示采用部分数据进行模型训练,可以降低模型的过拟合情况
推荐[0.5,0.8]:
3. 小节:Bagging、Boosting区别
1. 样本选择方式对比
Bagging思想是有放回的随机采样
Boosting思想是每一轮训练集不变
改变的是训练集样本在分类器的权重 / 目标属性y
权重 / y值都是根据上一轮的预测结果进行调整
2. 样本权重对比
Bagging思想使用随机抽样,样例是等权重
Boosting思想根据样本被分类错误与否,不断的调整样本的权重值,分类错误的样本权重大(Adaboost)
3. 预测函数
Bagging思想所有预测模型的权重相等
Boosting思想对于误差小的分类器具有更大的权重(Adaboost)
4. 并行计算
Bagging思想可以并行生成各个基模型
Boosting思想理论上只能顺序生产,因为后一个模型需要前一个模型的结果
5. 可解决问题
Bagging思想是减少模型的variance(方差)
基学习器分散,总模型几种
Boosting思想是减少模型的Bias(偏度)
基学习器不断更新模型,达到目标值
e
r
r
o
r
=
B
i
a
s
+
V
a
r
i
a
n
c
e
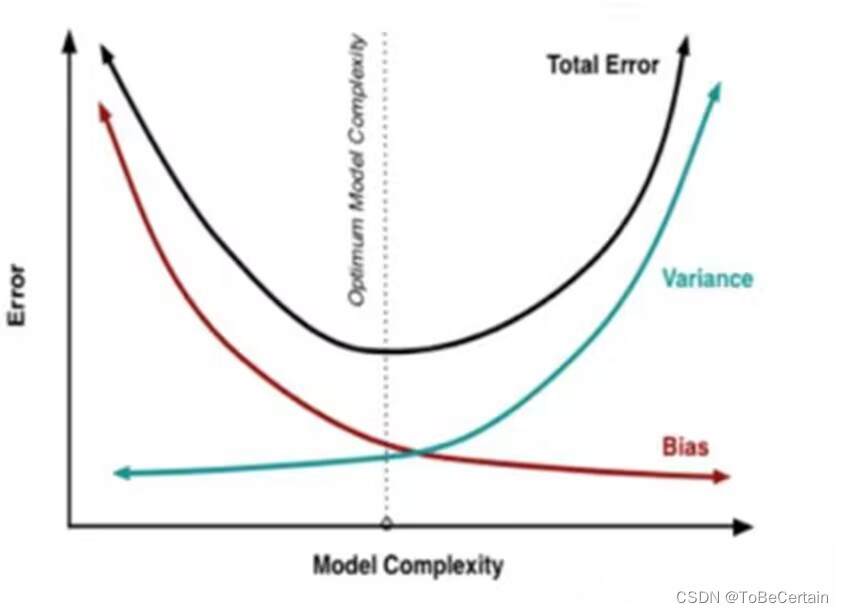
error = Bias + Variance
error=Bias+Variance
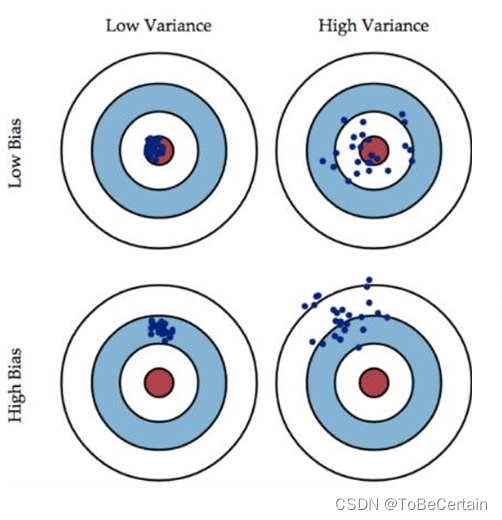
对于Low Variance & Low Bias:模型准确
对于High Variance & Low Bias:模型准但不确
方差大,过拟合现象 => bagging
对于Low Variance & High Bias:模型确但不准
偏度大,欠拟合现象 => boosting对于High Variance & High Bias:模型不准确
bagging是对许多强(甚至过强)的分类器求平均
此时每个单独的分类器bias都是低的,平均之后bias依然低;
然而每个单独的分类器variance都很高,平均之后就是降低这个variance
boosting是把许多弱分类器组合成一个强的分类器
Boosting是迭代算法,每一次迭代都根据上一次迭代的预测结果,对样本进行加权
随着迭代不断进行,误差会越来越小,所以模型的 bias 会不断降低;所以说boosting起到了降低bias的作用
variance不是boosting的主要考虑因素
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
本文相关代码存放位置
【Boosting思想 代码实现】
祝愉快🌟!