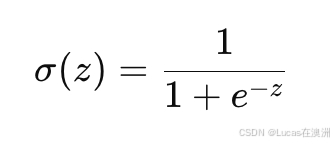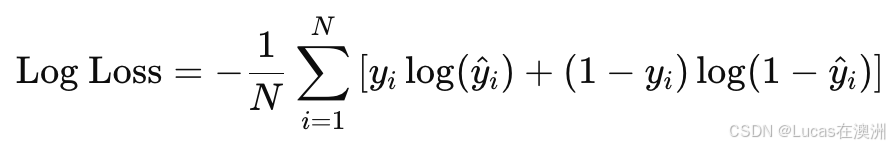Lucas带你手撕机器学习——逻辑回归

逻辑回归

简单理解逻辑回归

逻辑回归（Logistic Regression）是分类问题中常用的模型之一，尽管名字里有“回归”二字，但它实际上是用来做分类的。逻辑回归特别适合用于二分类问题，比如预测一封邮件是否是垃圾邮件、一个客户是否会购买某个产品等。

1. 逻辑回归的直观理解

假设我们要解决一个二分类问题，比如预测一个学生是否能通过考试。学生的学习时间 xxx 是输入特征，而“通过”或“未通过”是输出类别。逻辑回归就是要找到一种方法来将学生的学习时间转换成通过考试的概率。

在逻辑回归中，输出的概率会在 0 到 1 之间，表示某个事件发生的可能性。比如，某个学生学习了 5 个小时，逻辑回归模型预测他通过考试的概率是 0.85，就意味着模型认为这个学生有 85% 的概率会通过考试。

2. 逻辑回归的工作原理

逻辑回归的核心是 逻辑函数（也叫 sigmoid 函数），它的公式如下：

在这里插入图片描述

其中：

σ(z) 是 sigmoid 函数，将任意输入转换为 0 到 1 之间的值。
z 是线性回归的输出，即 z=wx+b

sigmoid 函数的形状像一个“S”形，它能将 z 的值（可以是任意实数）映射到 0 和 1 之间。具体来说：

当 z 很大时（例如，z→+∞），σ(z) 接近 1。
当 z 很小时（例如，z→−∞），σ(z) 接近 0。
当 z=0 时，σ(z)=0.5

3. 为什么用 sigmoid 函数？

sigmoid 函数的输出是一个概率值，可以用来判断某个样本属于哪个类别。比如：

如果 σ(z)>0.5，我们可以预测这个样本属于类别 1（通过考试）。
如果 σ(z)<0.5，我们可以预测这个样本属于类别 0（未通过考试）。

通过学习参数 w 和 b，逻辑回归模型能够找到最适合将输入 x 分类的分界线（决策边界）。

4. 损失函数与优化目标

为了训练逻辑回归模型，我们需要一个衡量模型好坏的指标，也就是损失函数。逻辑回归的损失函数是 对数损失（Log Loss），又叫 交叉熵损失（Cross-Entropy Loss）:

在这里插入图片描述

其中：

yi 是第 i 个样本的真实标签（0 或 1）。
y^i是第 i 个样本的预测概率值（通过 sigmoid 函数得到的）。

这个损失函数的目标是最大化模型的预测概率与真实值之间的相似度。我们通过梯度下降法来最小化这个损失函数，逐步调整 w 和 b，以找到最佳的分类模型。

5. 使用 Scikit-Learn 实现逻辑回归

下面是一个使用 Scikit-Learn 实现逻辑回归的简单例子：

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 生成模拟数据
np.random.seed(42)
X = np.random.rand(100, 1) * 10  # 学习时间（0到10小时）
y = (X > 5).astype(int).ravel()  # 如果学习时间超过5小时，标记为通过（1），否则为未通过（0）

# 拆分数据为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建逻辑回归模型并进行训练
model = LogisticRegression()
model.fit(X_train, y_train)

# 预测并计算准确率
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'模型在测试集上的准确率: {accuracy}')

# 输出模型的系数和截距
print(f'模型的权重（w）: {model.coef_[0]}')
print(f'模型的截距（b）: {model.intercept_[0]}')

在这里插入图片描述

6. 代码解释

生成模拟数据：创建了一些模拟数据，表示学生学习的时间 X 和是否通过的结果 y。学习时间超过 5 小时的标记为 1（通过），否则为 0（未通过）。
数据集拆分：将数据拆分成训练集和测试集，80% 用于训练，20% 用于测试。
训练模型：使用 LogisticRegression 类创建模型，并用训练集数据拟合模型。
预测和评估：使用测试集进行预测，并计算模型的准确率。

7. 代码解释

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score

# 步骤1：生成合成数据
X, y = make_classification(n_samples=1000, n_features=2, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 步骤2：标准化数据
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 将数据转换为 PyTorch 张量
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32).view(-1, 1)

# 步骤3：定义逻辑回归模型
class LogisticRegressionModel(nn.Module):
    def __init__(self, input_dim):
        super(LogisticRegressionModel, self).__init__()
        self.linear = nn.Linear(input_dim, 1)
    
    def forward(self, x):
        return torch.sigmoid(self.linear(x))

# 初始化模型、损失函数和优化器
input_dim = X_train.shape[1]
model = LogisticRegressionModel(input_dim)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 步骤4：训练模型
num_epochs = 100
for epoch in range(num_epochs):
    # 前向传播
    outputs = model(X_train)
    loss = criterion(outputs, y_train)
    
    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    # 每10个epoch打印一次损失
    if (epoch+1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 步骤5：评估模型
with torch.no_grad():
    y_pred = model(X_test)
    y_pred_class = y_pred.round()
    accuracy = accuracy_score(y_test, y_pred_class)
    print(f'Accuracy: {accuracy * 100:.2f}%')

数据生成：使用 sklearn 的 make_classification 创建适合二分类问题的合成数据集，然后将数据集拆分为训练集和测试集。
数据标准化：使用 StandardScaler 对特征进行归一化，提升模型训练效果。
模型定义：创建一个使用 PyTorch 的 nn.Module 的逻辑回归模型。它包含一个线性层，之后使用 sigmoid 激活函数将输出转换为概率。
模型训练：使用二元交叉熵损失函数 (BCELoss) 和随机梯度下降优化器 (SGD) 进行训练，训练100个epoch。
模型评估：对测试数据进行预测，并计算模型的准确率。

8. 总结

逻辑回归的核心思路是：

通过 wx+b 计算出一个线性结果 z，再通过 sigmoid 函数将这个结果转换为概率值。
概率值用于判断样本属于哪个类别（0 或 1）。
通过最小化对数损失（Log Loss）来优化模型参数，使得模型的预测更准确。

感谢阅读！！！我是正在澳洲深造的Lucas！！！
在这里插入图片描述