为了增加模型的非线性表达能力，引入了激活函数。为了不影响反向求导，对激活函数$f$有以下三点要求：
1、$f$要为连续可导函数
2、$f$的定义域为$R$
3、$f$是单调递增的$S$型曲线

1、基础知识

1）什么是饱和函数和非饱和函数？
饱和函数输入超出一定范围时，输出值接近于一个固定值，导致函数的导数接近于零。
非饱和函数在其输入范围内，输出值和导数都不会趋于饱和。
2）导数为饱和函数为什么会导致梯度消失？
在深度网络中，如果使用饱和函数，随着层数的增加，梯度在反向传播过程中会逐渐减小，因为饱和函数的导数接近于零。这就会导致早期的层难以学习，因为这些层的权重更新非常缓慢。
3）导数为非饱和函数为什么会导致梯度爆炸？
在非饱和函数中，尤其是在使用较大的学习率时，梯度可能会迅速增大，导致模型参数的更新过大，从而破坏模型的稳定性。梯度爆炸可能导致模型无法收敛，甚至造成数值溢出。
4）非零均值函数和零均值函数是什么？
在统计学和函数分析中，非零均值函数和零均值函数是指函数的均值（或期望值）是否为零。

2、sigmoid激活函数

$sigmoid$函数表达式如下：
$$\sigma =\frac{1}{1+e^{-y}}$$
$\sigma$对$y$求导，可得到对应的导数为$$\begin{gathered} \sigma =(\frac{1}{1+e^{-y}}{)}^{\prime }=\frac{e^{-y}}{(1+e^{-y}{)}^2} \\ =\frac{1}{1+e^{-y}}\times \frac{1+e^{-y}-1}{1+e^{-y}}=\sigma (1-\sigma ) \end{gathered}$$
其中$y$为预测值，通过激活函数可映射到0到1内。我们通过之前学习的matplotlib不难画出$sigmoid$函数及其导数的图像，具体代码如下：

from math import exp
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family']='STFangsong'
plt.figure()
figure,axes = plt.subplots(nrows=1,ncols=2,figsize=(20,8),dpi=80)
# 准备数据
x = list(np.linspace(-10,10,2000))
sigmoid = [1/(1+exp(-i)) for i in x]
sigmoid_grad=[i*(1-i) for i in sigmoid]
axes[0].plot(x,sigmoid,label='sigmoid')
axes[1].plot(x,sigmoid_grad,label='sigmoid_grad')
axes[0].set_title("sigmoid function")
axes[1].set_title("sigmoid_grad_function")
axes[0].grid(linestyle='--',alpha=0.5)
axes[1].grid(linestyle='--',alpha=0.5)
plt.show()

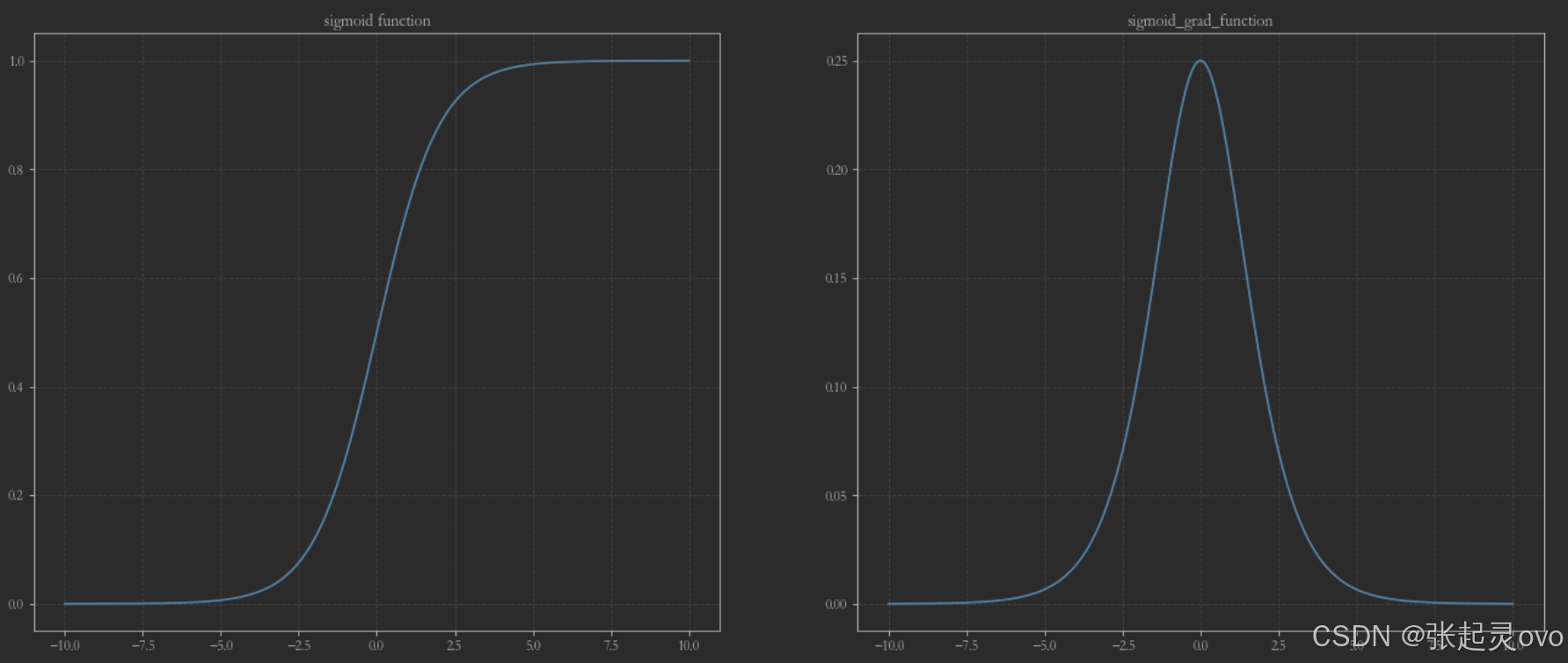
其图像如下所示：

观察发现，$sigmoid$函数的均值为$\frac{1}{2}$，不是非零均值函数，不易收敛(梯度变换缓慢)，其导数为饱和函数，容易导致梯度消失。

3、tanh激活函数

为了解决不易收敛的问题，采用$tanh$作为激活函数，其表达式如下:
$$tanh=\frac{1-e^{-y}}{1+e^{-y}}$$
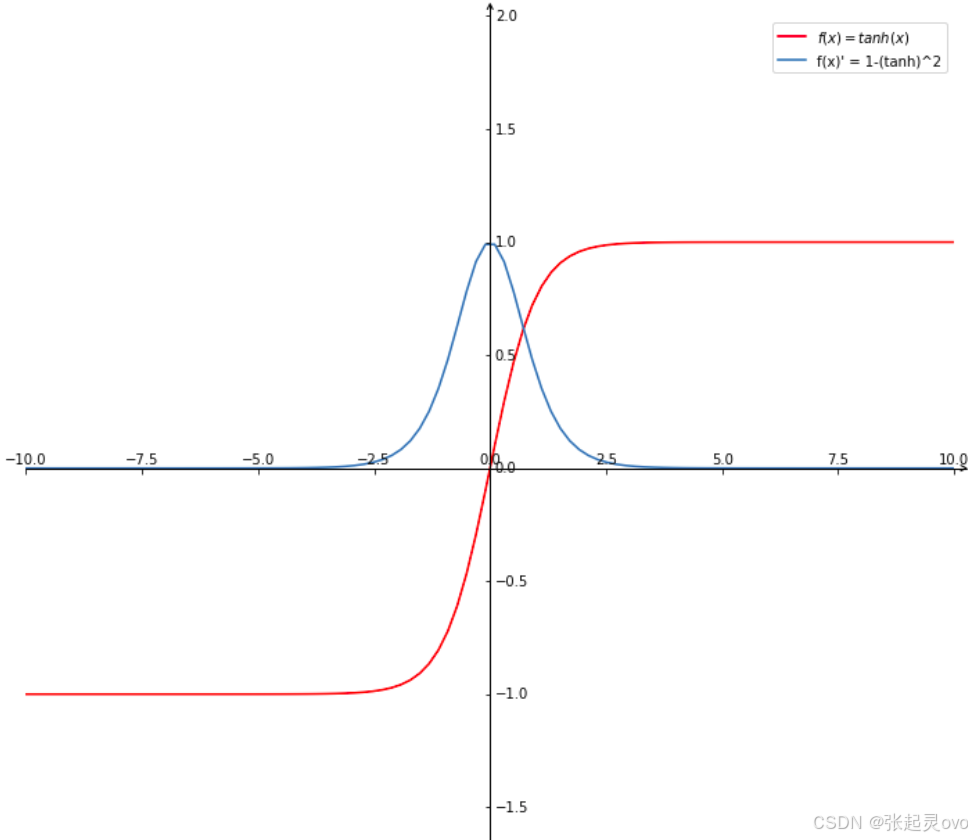
其图像同上修改对应函数关系即可画出来，如下所示：

可发现该函数是零均值函数，容易收敛，但是其导数仍然是饱和函数，容易导致梯度消失。

4、ReLu激活函数

全称：Rectified Linear Unit，即修正线性单元。其函数表达式如下：
$$relu(y)=\{\begin{array}{ll}y& y\ge 0\\ 0& y\le 0\end{array}$$
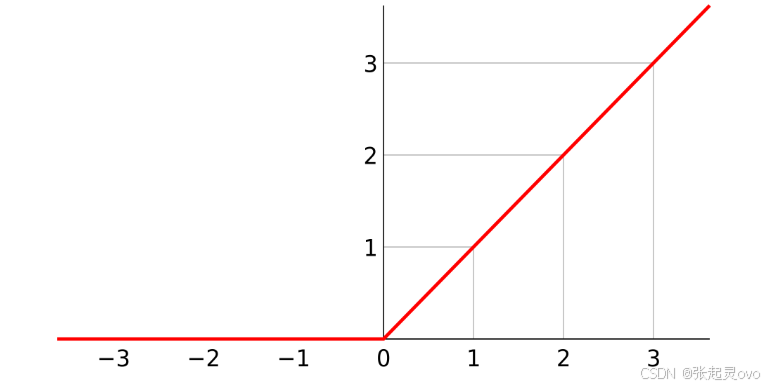
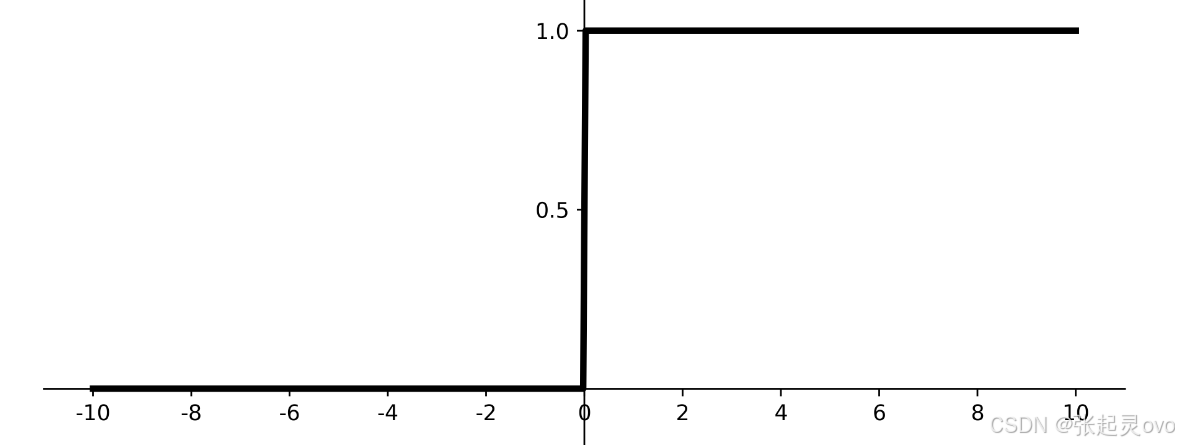
函数及其导数图形如下所示:

不难发现，该函数是非零均值函数，但是其计算简单，收敛速度快，而导数为非饱和函数，会导致梯度爆炸，解决这一问题的方案是进行参数初始化和归一化。$ReLu$函数是目前应用最广泛的激活函数。