使用FFT（快速傅里叶变换）实现高精度大整数乘法

一、题目

~~众所周知~~ ，快速傅里叶变换(Fast Fourier Transform, FFT)能够将计算DFT(离散傅里叶变换)的复杂度从只用DFT定义计算需要的 $O(n^2)$ ，降低到 $O(n\log n)$ ，其中 n 为数据大小,因此，FFT常被用于加速高精度乘法中。那么问题来了，给定两个非负整数 A 和 B ，请输出它们的乘积 $A * B$ 。

二、FFT

简单介绍

FFT是DFT的快速算法，它能够将多项式乘法转变成点值乘法，时间复杂度也从 $O(n^2)$ 降低到了 $O(n\log n)$ 。

如果将x=10代入多项式中，那么多项式的系数就是对应的数位，所以完全可以用FFT来进行大整数乘法的运算。

如何转换为点值乘法

假设我们现在有两个多项式，它们分别为

$\begin{aligned} &f(x) = 1+2x + 3x^2\\&g(x)=x + 2x^2\end{aligned}$

它们的乘积 $h(x)=f(x)g(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4$

如果取 $x = [1, 2, 3]$

x 1 2 3
h(x) 18 272 714

$\begin{bmatrix}a_0&a_1&a_2&a_3&a_4\end{bmatrix}* \begin{bmatrix}1&1&1\\x_0&x_1&x_2\\x_0^2&x_1^2&x_2^2\\x_0^3&x_1^3&x_2^3\\x_0^4&x_1^4&x_2^4\end{bmatrix} = \begin{bmatrix}h(x_0)&h(x_1)&h(x_2)\end{bmatrix}$

据此可以求出 $a_0,a_1,a_2,a_3,a_4$

x	1	2	3
h(x)	18	272	714

如果我们使用代码实现以上逻辑的话，时间复杂度为 $O(n^2)$ ，这并没有产生优化。

为什么呢？

这是因为我们的取值是随机的，那么就猜想如果对 $x_0,x_1...x_n$ 的取值符合某种规律，运用这种规律的性质是否可以产生优化。

答案是肯定的，这就需要用到复数的知识了：

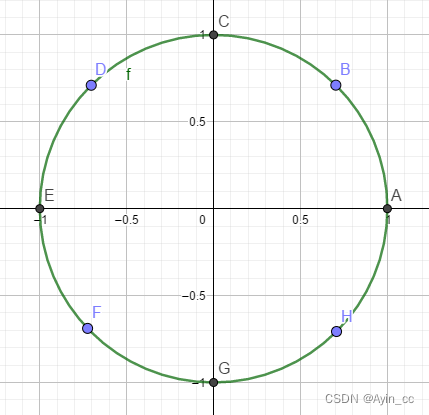
在这里插入图片描述

在复平面上，我们作出一个单位圆，易知 $x^8=1$ 的解为A、B…H这八个点，不妨把A点记为 $\omega_8^0$ ，将 $\omega_8^0$ 不断旋转45°后，我们可以依次得到 $\omega_8^1,\omega_8^2...\omega_8^7$ ，这些点对应着 $x^8=1$ 的解，所以 $\omega_8^8=\omega_8^0=1$ ，其中， $\omega_8$ 叫做旋转因子
而如果我们把 $x^8=1$ 变为 $x^4=1$ ， $\omega_8$ 变为 $\omega_4$ ，那么可以得到 $\omega_4^1=\omega_8^2,\omega_4^0=-\omega_8^4$

在知道了这些以后，我们就可以把 $x\in \{\omega_8^0,\omega_8^1...\omega_8^7\}$ 代入到 $f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7$ 中

$\begin{aligned} &f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7 \\ &x\in \{\omega_8^0,\omega_8^1...\omega_8^7\} \\ &f(x)=a_0x^0+a_2x^2+a_4x^4+a_6x^6+x(a_1x^0+a_3x^2+a_5x^4+a_7x^6) \\ &设p_1(x)=a_0x^0+a_2x^1+a_4x^2+a_6x^3,\ p_2(x)=a_1x^0+a_3x^1+a_5x^2+a_7x^3 \\ &那么f(x)=p_1(x^2)+xp_2(x^2),f(-x)=p_1(x^2)-xp_2(x^2) \\ &这就将1个8项多项式的计算转换成了2个4项多项式的子问题计算， \\ &这显然是分治的思想 \\ &之后再根据\omega_4^1=\omega_8^2,\omega_4^0=-\omega_8^4,就将子问题解决了 \\ &于是，我们就得到了 \\ &f(\omega_8^0)=p_1(w_4^0)+\omega_4^0p_2(\omega_4^0) \\ &f(\omega_8^1)=p_1(w_4^1)+\omega_4^1p_2(\omega_4^1) \\ &f(\omega_8^2)=p_1(w_4^2)+\omega_4^2p_2(\omega_4^2) \\ &f(\omega_8^3)=p_1(w_4^3)+\omega_4^3p_2(\omega_4^3) \\ &f(\omega_8^4)=f(\omega_8^4*\omega_8^0)=f(-\omega_4^0)=p_1(\omega_4^0)-\omega_4^0p_2(\omega_4^0) \\ &f(\omega_8^5)=p_1(w_4^1)-\omega_4^1p_2(\omega_4^1) \\ &f(\omega_8^6)=p_1(w_4^2)-\omega_4^2p_2(\omega_4^2) \\ &f(\omega_8^7)=p_1(w_4^3)-\omega_4^3p_2(\omega_4^3) \end{aligned}$

对f(x)进行的这种变换就叫做FFT（快速傅里叶变换）

补充

FFT的计算必须保证多项式的项数是2的整数次幂，如果不足的话，那就在后面补0（令系数为0）

三、IFFT

至此，我们已经解决了把多项式乘法转换成点值乘法的问题，即 $A*\Omega\stackrel{FFT}{\Rightarrow} R$

$A=\begin{bmatrix}a_0&a_1&a_2&a_3&a_4&a_5&a_6&a_7\end{bmatrix},\ \Omega=\begin{bmatrix}\omega^{0*0}&\omega^{1*0}&\omega^{2*0}&\omega^{3*0}&\omega^{4*0}&\omega^{5*0}&\omega^{6*0}&\omega^{7*0}\\\omega^{0*1}&\omega^{1*1}&\omega^{2*1}&\omega^{3*1}&\omega^{4*1}&\omega^{5*1}&\omega^{6*1}&\omega^{7*1}\\\omega^{0*2}&\omega^{1*2}&\omega^{2*2}&\omega^{3*2}&\omega^{4*2}&\omega^{5*2}&\omega^{6*2}&\omega^{7*2}\\\omega^{0*3}&\omega^{1*3}&\omega^{2*3}&\omega^{3*3}&\omega^{4*3}&\omega^{5*3}&\omega^{6*3}&\omega^{7*3}\\\omega^{0*4}&\omega^{1*4}&\omega^{2*4}&\omega^{3*4}&\omega^{4*4}&\omega^{5*4}&\omega^{6*4}&\omega^{7*4}\\\omega^{0*5}&\omega^{1*5}&\omega^{2*5}&\omega^{3*5}&\omega^{4*5}&\omega^{5*5}&\omega^{6*5}&\omega^{7*5}\\\omega^{0*6}&\omega^{1*6}&\omega^{2*6}&\omega^{3*6}&\omega^{4*6}&\omega^{5*6}&\omega^{6*6}&\omega^{7*6}\\\omega^{0*7}&\omega^{1*7}&\omega^{2*7}&\omega^{3*7}&\omega^{4*7}&\omega^{5*7}&\omega^{6*7}&\omega^{7*7}\end{bmatrix}$

现在，我们要做的就是根据 $R$ 求出 $A$ ,这一步叫做IFFT（逆快速傅里叶变换）

即 $R*\Omega^{-1}\stackrel{IFFT}{\Rightarrow}A$

$\Omega$ 矩阵本质上是个范德蒙德矩阵，我们可以根据性质得到其逆矩阵为

$\Omega^{-1}=\frac18\begin{bmatrix}\tau^{0*0}&\tau^{1*0}&\tau^{2*0}&\tau^{3*0}&\tau^{4*0}&\tau^{5*0}&\tau^{6*0}&\tau^{7*0}\\\tau^{0*1}&\tau^{1*1}&\tau^{2*1}&\tau^{3*1}&\tau^{4*1}&\tau^{5*1}&\tau^{6*1}&\tau^{7*1}\\\tau^{0*2}&\tau^{1*2}&\tau^{2*2}&\tau^{3*2}&\tau^{4*2}&\tau^{5*2}&\tau^{6*2}&\tau^{7*2}\\\tau^{0*3}&\tau^{1*3}&\tau^{2*3}&\tau^{3*3}&\tau^{4*3}&\tau^{5*3}&\tau^{6*3}&\tau^{7*3}\\\tau^{0*4}&\tau^{1*4}&\tau^{2*4}&\tau^{3*4}&\tau^{4*4}&\tau^{5*4}&\tau^{6*4}&\tau^{7*4}\\\tau^{0*5}&\tau^{1*5}&\tau^{2*5}&\tau^{3*5}&\tau^{4*5}&\tau^{5*5}&\tau^{6*5}&\tau^{7*5}\\\tau^{0*6}&\tau^{1*6}&\tau^{2*6}&\tau^{3*6}&\tau^{4*6}&\tau^{5*6}&\tau^{6*6}&\tau^{7*6}\\\tau^{0*7}&\tau^{1*7}&\tau^{2*7}&\tau^{3*7}&\tau^{4*7}&\tau^{5*7}&\tau^{6*7}&\tau^{7*7}\end{bmatrix},\tau=\omega^{-1}$

这样一来，求IFFT与求FFT没有什么区别了，因此求FFT的函数也可用于求IFFT，我们只需要引入一个参数inverse，若其为true，则是求IFFT，将 $\omega$ 变为 $\tau$ ，若为false，就是求FFT

四、代码

根据以上思路，我们的代码逻辑如下

#include <iostream>
#include <vector>
#include <cmath>
#include <complex>

using namespace std;

const double PI = acos(-1.0);

// 递归实现FFT
void fft(vector<complex<double>>& a, bool inv) {
    int n = a.size();
    if (n == 1) {
        return;
    }
    
    //分治
    vector<complex<double>> a0(n / 2), a1(n / 2);
    for (int i = 0, j = 0; i < n; i += 2, j++) {
        a0[j] = a[i];
        a1[j] = a[i + 1];
    }
    fft(a0, inv);
    fft(a1, inv);
    
    //FFT
    double angle = 2 * PI / n * (inv ? -1 : 1);
    complex<double> w(1), wn(cos(angle), sin(angle));
    for (int i = 0; i < n / 2; i++) {
        a[i] = a0[i] + w * a1[i];
        a[i + n / 2] = a0[i] - w * a1[i];
        w *= wn;
    }
}

// FFT乘法
vector<int> multiply(vector<int> a, vector<int> b) {
    int n = 1;
    // 将多项式的项数变为2的整数次幂
    while (n < a.size() + b.size()) {
        n *= 2;
    }
    a.resize(n), b.resize(n);
    
    vector<complex<double>> c(n), d(n);
    for (int i = 0; i < n; i++) {
        c[i] = complex<double>(a[i], 0);
        d[i] = complex<double>(b[i], 0);
    }
    
    // 求原多项式的FFT
    fft(c, false), fft(d, false);
    for (int i = 0; i < n; i++) {
        c[i] *= d[i];
    }
    
    // 求乘法结果的IFFT
    fft(c, true);
    
    // 将IFFT中与逆矩阵相差的1/n乘进去
    vector<int> res(n);
    for (int i = 0; i < n; i++) {
        res[i] = (int)(c[i].real() / n + 0.5);
    }
    
    // 处理进位
    int carry = 0;
    for (int i = 0; i< n; i++) {
    	res[i] += carry;
    	carry = res[i] / 10;
    	res[i] %= 10;
	}
    
    // 去高位的0
	while (res.size() > 1 && res.back() == 0) {
    	res.pop_back();
	}
	return res;
}

// 将大整数字符串转换为vector<int>
vector<int> to_vector(string s) {
	vector<int> res;
	for (int i = s.size() - 1; i >= 0; i--) {
		res.push_back(s[i] - '0');
	}
	return res;
}

// 将vector<int>转换为大整数字符串
string to_string(vector<int> a) {
	string res;
	for (int i = a.size() - 1; i >= 0; i--) {
		res += to_string(a[i]);
	}
	return res;
}

int main() {
	string s1, s2;
	cin >> s1 >> s2;
	vector<int> a = to_vector(s1), b = to_vector(s2);
	vector<int> c = multiply(a, b);
	cout << to_string(c) << endl;
	return 0;
}