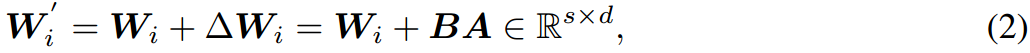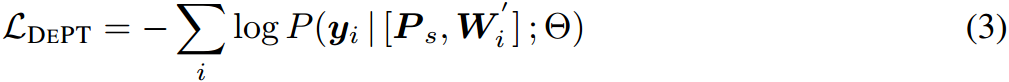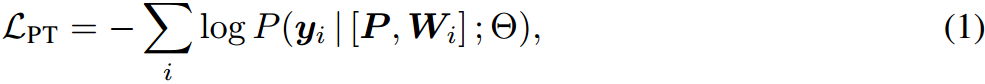论文汇总
当前的问题
(1)Prompt Tuning通常收敛缓慢,并且对初始化敏感;
(2)Prompt Tuning延长了输入序列的总长度,从而加剧了计算需求(即训练/推理时间和内存成本),这是由于Transformer的二次复杂度(Vaswani et al, 2017)。
解决办法
个人理解:Prompt Tuning和LoRA的简单结合
提示分解
将可训练提示矩阵 P ∈ R l × d \bm{P} \in \mathbb{R}^{l\times d} P∈Rl×d分解为两个部分:
(1)更短的可训练提示矩阵 P s ∈ R m × d \bm{P}_s \in \mathbb{R}^{m\times d} Ps∈Rm×d;
(2)一对低秩矩阵, A ∈ R s × r \bm{A} \in \mathbb{R}^{s\times r} A∈Rs×r和 B ∈ R s × d \bm{B} \in \mathbb{R}^{s\times d} B∈Rs×d,其中矩阵的秩 r ≪ m i n ( s , d ) r \ll min(s,d) r≪min(s,d)。
其中, W i W_i Wi被冻结,在训练过程中不接受梯度更新,而 A A A和 B B B是可训练的。根据Hu et al(2021),我们对 A A A使用随机高斯初始化,对 B B B使用零初始化,因此训练开始时 Δ W = B A \Delta W=BA ΔW=BA为零。然后将损失函数优化如下:
为了保持与Prompt Tuning训练才参数一致,作者选择 m m m和 r r r的值来满足方程 l × d = m × d + ( s + d ) × r l\times d=m\times d+(s+d)\times r l×d=m×d+(s+d)×r。
但与普通Prompt Tuning相比,该设计提高了内存效率并降低了计算成本,因为较短的输入序列长度(即 m + s < l + s m+s<l+s m+s<l+s)大大减少了计算量,这是由于Transformer的二次复杂度(解决了问题1)。
两种学习速率
DEPT在训练上也不同于普通的PT。我们用学习率 α 1 \alpha_1 α1来训练较短的可训练提示矩阵 P s \bm{P}_s Ps,用学习率 α 2 \alpha_2 α2来训练一对低秩矩阵 A A A和 B B B,而不是像在普通Prompt Tuning中那样使用单一学习率。 α 1 \alpha_1 α1通常比 α 2 \alpha_2 α2大得多。
摘要
提示调整(PT)是将少量可训练的软(连续)提示向量附加到模型输入上的方法,在参数有效微调(PEFT)的各种任务和模型架构中显示出有希望的结果。PT从其他PEFT方法中脱颖而出,因为它使用较少的可训练参数保持有竞争力的性能,并且不会随着模型大小的扩展而急剧扩展其参数。然而,PT引入了额外的软提示令牌,导致更长的输入序列,由于Transformer的二次复杂度,这极大地影响了训练/推理时间和内存使用。特别是对于面临大量日常查询的大型语言模型(LLM)。为了解决这个问题,我们提出了分解提示调整(DEPT),它将软提示分解为一个较短的软提示和一对低秩矩阵,然后用两种不同的学习率进行优化。这使得DEPT在不改变可训练参数大小的情况下,与普通PT及其变体相比,在节省大量内存和时间成本的同时,获得更好的性能。通过对23个自然语言处理(NLP)和视觉语言(VL)任务的广泛实验,我们证明了DEPT在某些情况下优于最先进的PEFT方法,包括完全微调基线。此外,我们的经验表明,随着模型规模的增加,DEPT的效率会提高。我们进一步的研究表明,DEPT在少样本学习设置下与参数高效迁移学习无缝集成,并突出了其对各种模型架构和大小的适应性。
1.介绍
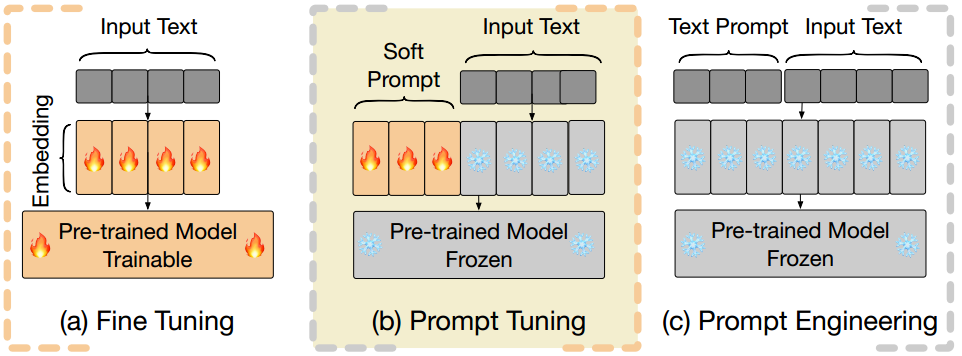
图1:完全微调(FT)、提示微调优(PT)和提示工程的概述PT增加了输入序列的长度,导致训练和推理短语期间的计算需求大得多。
微调(FT)语言模型(LMs) (rafael等,2020;Touvron等人,2023)在下游任务上提供了跨各种自然语言处理(NLP)任务的巨大性能改进,但它需要更新和存储LMs的全部参数(见图1a),当LMs包含数亿甚至数十亿个参数时,这尤其昂贵。提示工程(Brown et al, 2020)不更新任何参数,而通常难以设计并且具有高性能方差(Wang et al, 2023a)(见图1c)。因此,参数高效微调(PEFT)方法(Liu et al ., 2022)吸引了越来越多的兴趣,旨在每个任务只学习少量参数,同时保持与完全微调相当的性能水平。
提示调整(PT) (Lester等人,2021)已经成为一种很有前途的PEFT方法,它将可训练的连续提示向量附加到输入(见图1b)。PT从其他PEFT方法中脱颖而出,因为它使用较少的可训练参数保持有竞争力的性能,并且随着模型规模的扩大,它的可训练参数不会急剧扩大。最近的研究表明,LM的大部分知识是在预训练阶段获得的(Zhou et al ., 2023)并且上下文学习(ICL)只需几个精心设计的风格示例和精心设计的系统提示符就可以获得令人印象深刻的对齐结果(Lin et al, 2023)。考虑到任务已经在一定程度上被LMs理解的场景,关键的挑战只是正确地提示LMs, PT作为其他PEFT方法的潜在更好的选择出现。
虽然PT在各种任务和模型中显示出令人鼓舞的结果,但它有两个主要局限性**:(1)PT通常收敛缓慢,并且对初始化敏感(Lester et al ., 2021;Vu等,2022;Wang et al ., 2023b);(2) PT延长了输入序列的总长度,从而加剧了计算需求(即训练/推理时间和内存成本),这是由于Transformer的二次复杂度(Vaswani et al, 2017)。考虑到缓慢的趋同问题,这一点更加突出。近期研究(Su et al ., 2022;Vu等,2022;Li等人,2022)提出了香草PT的变体,通过在各种源任务上初始预训练软提示来解决第一个问题,这被称为参数有效迁移学习(PETL),如图2a所示。一些研究(Asai et al, 2022;Wang等人,2023b)也通过在多个目标任务上联合训练来自这些源任务的学习提示(称为多任务学习)来提高PT的性能。然而,由于序列长度的延长而增加的计算负荷问题在很大程度上仍然没有得到解决**。虽然PETL方法可以减少模型收敛的训练步骤,但每个优化步骤在时间和内存方面仍然是计算昂贵的。最重要的是,它并没有提高推理阶段的效率,这在大型语言模型(LLMs)时代尤为重要,因为训练好的模型每天可能被查询数百万次。
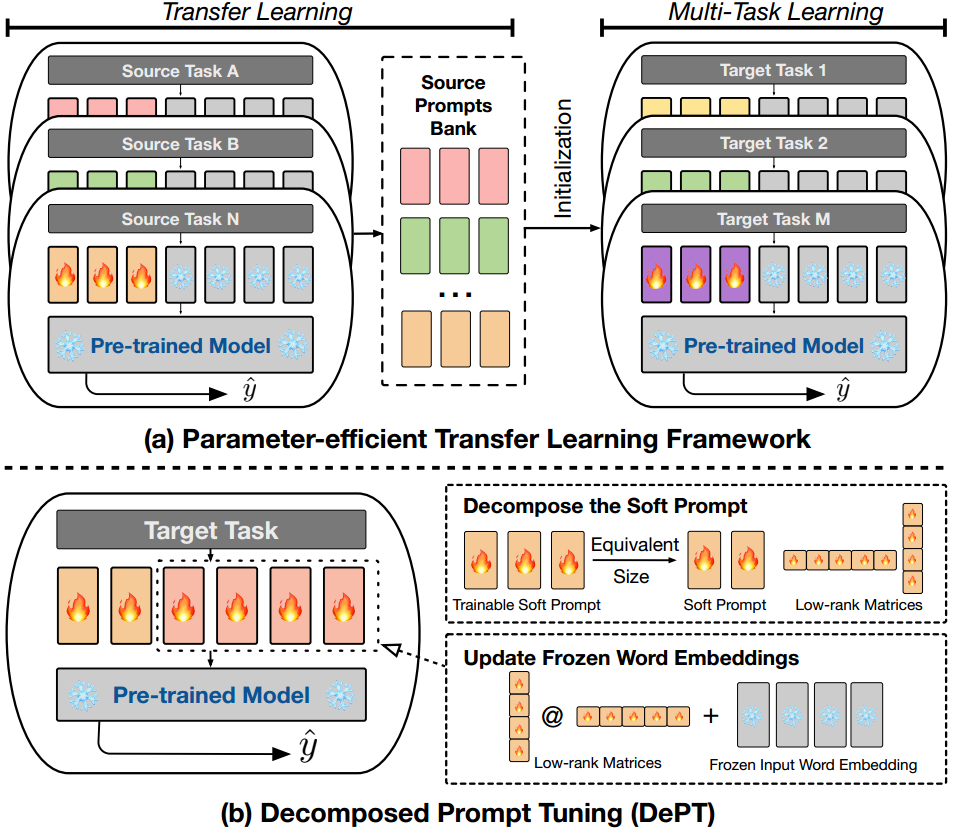
在这项工作中,我们提出了分解提示调优(DEPT),它将可训练的软提示分解为更短的软提示和几个低秩矩阵,然后将低秩矩阵的乘法添加到冻结的词嵌入中,如图2b(§2.2)所示。这个较短的软提示和更新的词嵌入矩阵然后使用两种不同的学习率进行优化-这是模型收敛的关键步骤(§3.4)。这种设计的直觉是在冻结的词嵌入中启用表示更新,从而增加了以前不可用的输入表示的适应性。在23个自然语言处理(NLP)和视觉语言(VL)任务上的实验结果表明,DEPT优于最先进的PEFT方法,包括在某些场景下的完全微调基线(§3.2)。我们的实证研究表明,DEPT在很大程度上提高了各种模型架构和大小的训练效率,与香草PT相比,在训练时间和内存成本上节省了20%以上(使用T5-BASE)。重要的是,随着模型大小的增长,DEPT变得越来越高效,使其特别具有优势,适合LLMs(§3.3)。此外,我们在少样本学习设置中的附加分析揭示了DEPT与PETL方法的兼容性(§3.4)。
综上所述,本文的主要贡献如下:
•我们提出了DEPT方法,该方法通过分解其软提示来减少输入序列长度,从而解决了提示调谐的关键效率限制。在时间和内存成本方面,DEPT极大地提高了训练和推理效率;
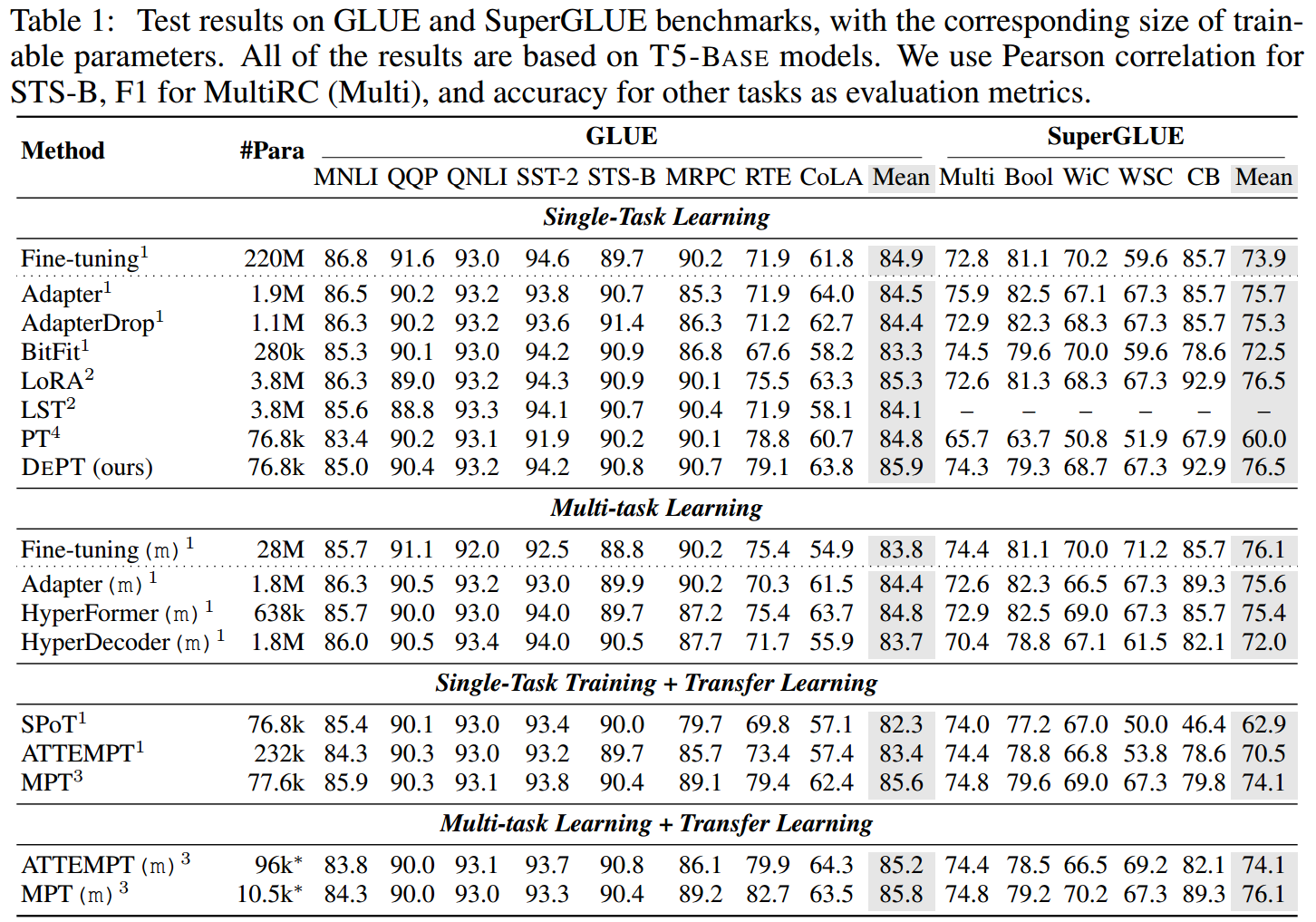
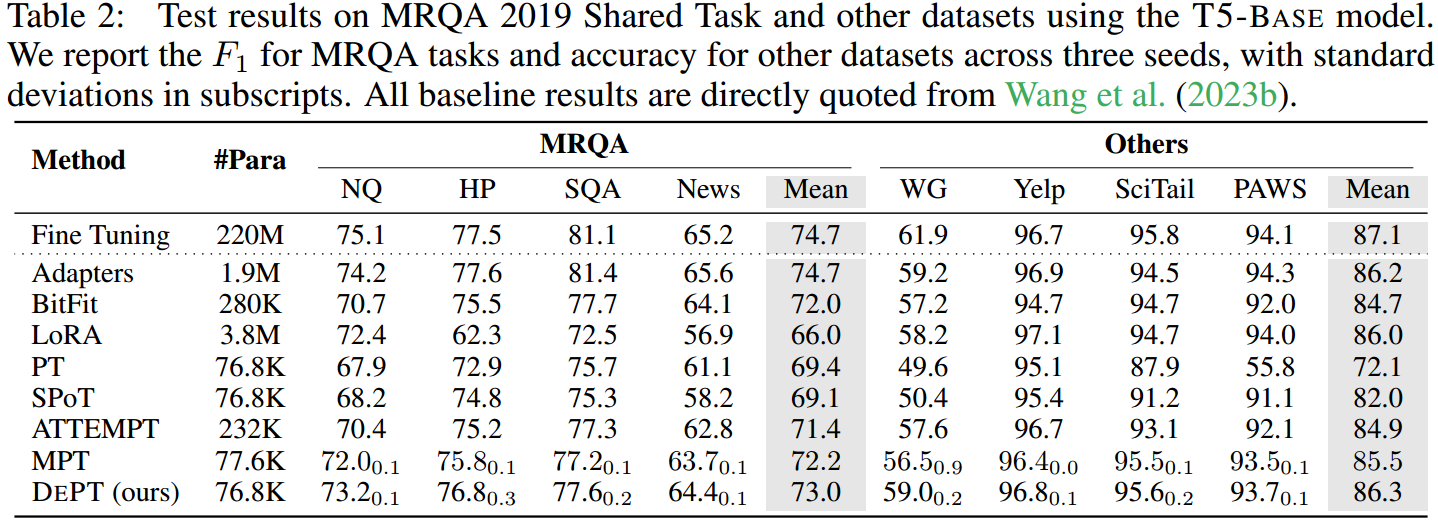
•我们对23个NLP和VL任务的综合评估表明,DEPT优于最先进的PEFT方法,包括在某些情况下的全面微调。
此外,我们的实验表明,DEPT与PETL方法可以很好地集成,并且在少样本学习环境下,DEPT的优势仍然存在;
•我们的经验表明,随着模型规模的增长,DEPT变得越来越高效,使其特别适合LLMs。此外,DEPT与各种PEFT方法(即Adapter、LoRA)是正交的,可以很容易地组合在一起。
2.方法
在本节中,我们首先回顾§2.1中的提示调优(PT)的背景,然后介绍我们提出的方法,§2.2中的分解提示调优(DEPT)。
2.1 背景:提示微调(PT)
令 L ≜ { x i , y i } i = 1 N L\triangleq \{x_i,y_i\}^N_{i=1} L≜{xi,yi}i=1N表示目标任务 τ \tau τ的 N N N个标记训练数据。给定一个参数化为 Θ \Theta Θ的主干模型,每个输入文本 x i x_i xi被映射到一个词嵌入序列 W i ∈ R s × d W_i \in \mathbb{R}^{s\times d} Wi∈Rs×d中,其中 s s s和 d d d表示词嵌入的最大序列长度和维数。PT将一个可训练的提示矩阵 P ∈ R l × d \bm{P}\in \mathbb{R}^{l\times d} P∈Rl×d附加到冻结的词嵌入矩阵 W i W_i Wi中,其中 l l l是虚拟令牌数量的超参数。软提示符 P \bm{P} P可以随机初始化,也可以通过从词汇表中采样单词嵌入来初始化。因此,模型的输入成为组合矩阵 [ P ; W i ] ∈ R ( l + s ) × d [\bm{P} ;W_i] \in \mathbb{R}^{(l+s)\times d} [P;Wi]∈R(l+s)×d。目标损失函数表示为:
其中损失函数仅相对于软提示矩阵 P \bm{P} P进行优化。
2.2 我们的方法:分解提示调优(dept)
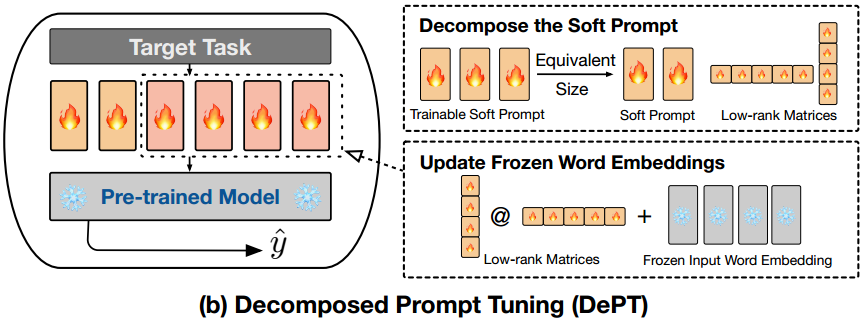
分解软提示。DEPT在输入方面与普通PT方法不同。如图2b所示,我们将香草PT中的可训练提示矩阵 P ∈ R l × d \bm{P} \in \mathbb{R}^{l\times d} P∈Rl×d分解为两个部分:(1)更短的可训练提示矩阵 P s ∈ R m × d \bm{P}_s \in \mathbb{R}^{m\times d} Ps∈Rm×d;(2)一对低秩矩阵, A ∈ R s × r \bm{A} \in \mathbb{R}^{s\times r} A∈Rs×r和 B ∈ R s × d \bm{B} \in \mathbb{R}^{s\times d} B∈Rs×d,其中矩阵的秩 r ≪ m i n ( s , d ) r \ll min(s,d) r≪min(s,d)。第一个组件,较小的可训练提示矩阵,以与香草PT类似的方式附加到词嵌入矩阵中。第二个组件使用两个低秩矩阵的乘法来表示通过坐标明智和更新词嵌入:
其中, W i W_i Wi被冻结,在训练过程中不接受梯度更新,而 A A A和 B B B是可训练的。根据Hu et al(2021),我们对 A A A使用随机高斯初始化,对 B B B使用零初始化,因此训练开始时 Δ W = B A \Delta W=BA ΔW=BA为零。然后将损失函数优化如下:
在我们的实验中,我们选择 m m m和 r r r的值来满足方程 l × d = m × d + ( s + d ) × r l\times d=m\times d+(s+d)\times r l×d=m×d+(s+d)×r,以保持与香草PT中相同的可训练参数的确切大小。因此,当 r > 0 r>0 r>0时, m m m总是小于 l l l。与普通PT相比,该设计提高了内存效率并降低了计算成本,因为较短的输入序列长度(即 m + s < l + s m+s<l+s m+s<l+s)大大减少了计算量,这是由于Transformer的二次复杂度(Vaswani et al, 2017)。
两种学习速率。DEPT在训练上也不同于普通的PT。我们用学习率 α 1 \alpha_1 α1来训练较短的可训练提示矩阵 P s \bm{P}_s Ps,用学习率 α 2 \alpha_2 α2来训练一对低秩矩阵 A A A和 B B B,而不是像在普通PT中那样使用单一学习率。 α 1 \alpha_1 α1通常比 α 2 \alpha_2 α2大得多。我们将在§3.4中实证验证这个选择的重要性。然而,DEPT可能会为超参数优化引入额外的训练成本(见§5)。
3.实验与结果
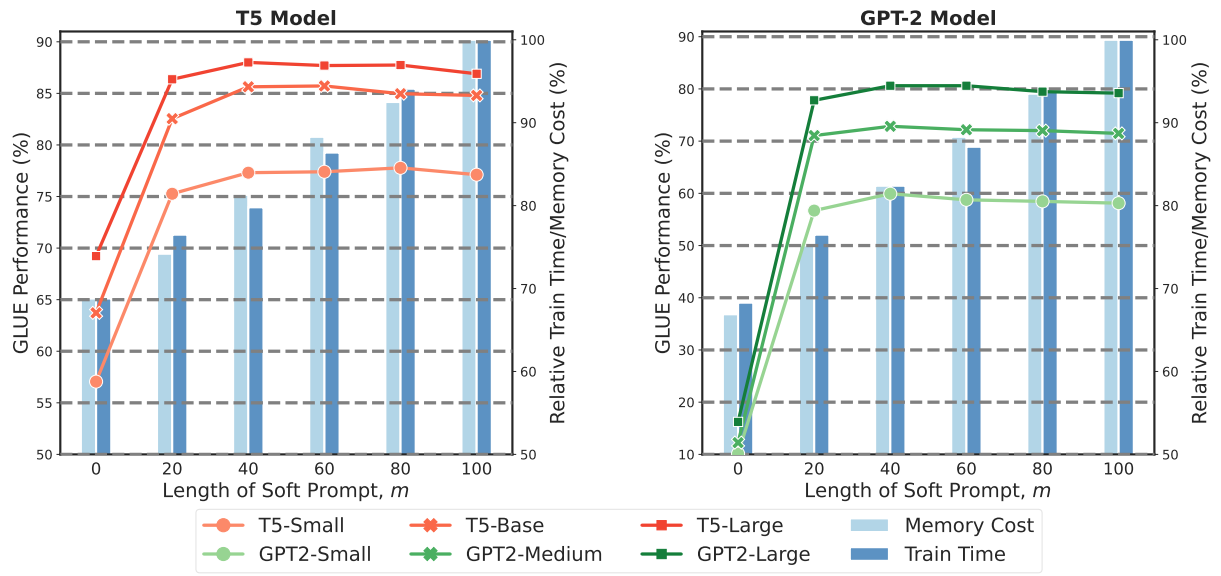
图3:在DEPT中不同软提示长度m的GLUE基准上的性能,与相应的相对训练时间和内存成本相关。使用批处理大小为16,对不同模型大小的时间和内存进行平均。DEPT始终使用与普通PT相同数量的可训练参数(m=100)。
图4:在保持可训练参数总数不变的情况下,使用不同软提示长度m和低秩矩阵秩r的GLUE基准上的平均推理速度。蓝色的小文本表示相对于香草PT(用棕色表示)的速度(m=100)。
4.相关工作
Parameter-efficient微调。与标准微调和基于提示的微调相比(Devlin等人,2019;Schick & Schutze¨,2021;Shi & Lipani, 2023),其中全参数更新,参数有效微调(PEFT)方法在广泛的任务中表现出卓越的性能(Wang等人,2018;Shi et al ., 2022;Wu等,2023a;Hendriksen等人,2022;Wu等,2023b;Yang et al ., 2023),同时只更新有限数量的参数。适配器(Houlsby等人,2019)及其变体HyperFormer (Karimi Mahabadi等人,2021)和compter (Mahabadi等人,2021)为T5模型的每个变压器块添加了新的可训练模块(适配器)(Raffel等人,2020)。BitFit (Ben Zaken et al, 2022)只对偏差参数进行更新,而这种方法在较大的网络上往往表现不佳(Lialin et al, 2023)。前缀调谐(Li & Liang, 2021)为模型输入添加了一个由前馈网络参数化的软提示。Diff剪枝(Guo et al ., 2021)以更多内存使用为代价学习神经网络权值的稀疏更新。FishMask (Sung et al ., 2021)也执行稀疏更新,但它在当代深度学习硬件上计算密集且效率低下(Lialin et al ., 2023)。LoRA (Hu et al ., 2021;Yang等人,2024)采用直接的低秩矩阵分解来参数化权重更新。(IA)3 (Liu et al ., 2022)通过学习向量对少样本学习进行缩放激活。LST (Sung et al ., 2022b)在预训练网络的一侧运行一个小型变压器网络,旨在减少训练记忆。提示调整(PT) (Lester等人,2021)将可训练的软提示附加到模型输入嵌入中。与上述PEFT方法相比,PT使用较少的可训练参数,这些参数不会随着模型大小的扩展而激增。Mao等人(2022)介绍了一种通过门控机制将前缀调优、适配器和LoRA结合在一起的方法。DEPT也适用于这种方法,并且可以很容易地与其他PEFT方法集成。
PT的迁移学习。最近的研究旨在通过迁移学习来提高PT的表现。PPT (Gu et al ., 2022)通过进一步的预训练努力提高PT (Lester et al ., 2021)的性能(Gururangan et al ., 2020;Shi等人,2023),这需要一套手工制作的、特定于任务的设计和可观的计算成本。Su等人(2022)通过跨不同任务和模型的快速迁移提高了PT。SPoT (Vu et al ., 2022)采用基于相似性度量的单一提示,以大规模搜索为代价。ATTEMPT (Asai et al, 2022)在源提示上采用了一种注意机制,以额外的参数为代价初始化目标任务的提示。MPT (Wang et al ., 2023b)在不同的任务之间应用共享的软提示,而其对大范围源任务的有效性尚未经过测试。我们发现PETL对于PT (Asai et al ., 2022;Wang et al ., 2023b)可以有效地加速训练收敛,并且用于PT的PETL对于在PT的少样本学习设置下提高模型性能更有用(Gu et al ., 2022;Wu et al ., 2022)。然而,当有广泛的标记数据集可用时,训练PT或DEPT进行额外的步骤通常会导致性能改进。
5.结语
结论。在这项工作中,我们提出了分解提示调优(DEPT),它在时间和内存方面大大提高了香草PT的效率,同时与最先进的PEFT方法相比,提供了具有竞争力甚至更好的性能。值得注意的是,DEPT效率随着模型大小的增加而扩大,使其特别适合LLMs。我们进一步的分析显示了DEPT与PETL方法的兼容性,并强调了它在不同模型体系结构和规模上的通用性。
局限性和未来的工作。我们概述了我们工作中的几个限制:(1)DEPT的主要限制是引入额外的超参数进行调优,例如,低秩矩阵的学习率。这可能会在模型训练的超参数优化阶段引入一些额外的计算开销。在我们的工作中,我们训练DEPT达到30万步(在数据丰富的环境中)(Vu et al, 2022),并仔细寻找最佳学习率,这可能会增加训练成本。然而,PETL可以有效地减少训练步骤的数量,我们计划在未来的工作中对此进行研究。此外,重要的是要注意模型训练过程是一次性事件,而模型推理不是。在这种背景下,DEPT的效率效益变得尤为重要;(2) DEPT中可训练参数的数量取决于最大序列长度 s s s。在这项工作中,我们将评估限制在具有数百个输入令牌的任务上。未来的工作可以探索当 s s s非常大时DEPT的性能;(3)我们的研究重点是利用LMs的提示技术,之前的研究(Bender & Koller, 2020;Brown et al, 2020;Bender等人,2021)已经解决了与LMs相关的担忧和潜在危害。
参考资料
论文下载(ICLR 2024)
https://arxiv.org/pdf/2309.05173