写在前面：
🌟 欢迎光临 清流君 的博客小天地，这里是我分享技术与心得的温馨角落。📝
个人主页：清流君_CSDN博客，期待与您一同探索 移动机器人 领域的无限可能。

🔍 本文系 清流君 原创之作，荣幸在CSDN首发🐒
若您觉得内容有价值，还请评论告知一声，以便更多人受益。
转载请注明出处，尊重原创，从我做起。

👍 点赞、评论、收藏，三连走一波，让我们一起养成好习惯😜
在这里，您将收获的不只是技术干货，还有思维的火花！

📚 系列专栏：【运动控制】系列，带您深入浅出，领略控制之美。🖊
愿我的分享能为您带来启迪，如有不足，敬请指正，让我们共同学习，交流进步！

🎭 人生如戏，我们并非能选择舞台和剧本，但我们可以选择如何演绎 🌟
感谢您的支持与关注，让我们一起在知识的海洋中砥砺前行~~~

引言

  模型预测控制（Model Predictive Control，MPC）是一种先进的控制策略，它通过构建一个数学模型来预测系统的未来行为，并使用这个模型来优化控制输入，以达到特定的性能指标。
  本文从运动学模型角度出发，利用MPC算法设计具有轨迹跟踪功能的控制器，在给定期望轨迹点的情况下，完成对期望轨迹的跟踪控制。使用Python语言编写程序，对所设计的控制器进行仿真验证。本文将理论与实践相结合，在介绍完轨迹跟踪控制器的理论算法后，通过实例进一步加深对理论的认知。

  关于MPC算法的详细推导可参考其他资料，本文重在应用算法进行车辆的控制器设计。

  本文所研究的车辆模型为阿克曼转向的车辆，前轮转向，后轮驱动。

一、MPC核心思想与基本原理

  在每一个采样时刻 $k$ 获得当前测量信息，在线地求解有限时域下的优化问题，预测未来一段时间内系统行为，并且在每个控制周期内将得到的 控制序列中的第一个值 作用到被控对象中，使得在这段时间内系统的性能指标达到最优，在下一个采样时刻重复上述过程，用新的测量值刷新优化问题，并重新求解。

二、MPC的基本工作流程

1、系统建模

  首先，需要对系统进行建模，通常采用状态空间模型，需要对象的系统状态量和输入控制量。这个模型描述了系统的动态行为，包括状态变量、控制输入和系统参数等。

  以车辆的轨迹跟踪为例，状态量包括车辆当前的位置、航向角，控制量包括车辆的前轮转角、后轮速度。

2、目标函数定义

  定义一个性能指标，将预测的输出与期望的输出做比较，要使得这个差别最小化，也就是代价函数。用来衡量系统行为的优劣。这个代价函数通常包括系统状态、控制输入和参考轨迹之间的差异，以及对终端误差的惩罚项。

3、约束条件设置

  设置系统的约束条件，包括状态约束、控制输入约束和其他约束条件，如碰撞避免、车辆最大速度和最大转角等。

4、优化问题求解

  在每个控制时刻，通过求解一个优化问题来确定当前时刻的最优控制输入。这个优化问题的目标是最小化目标函数，同时满足约束条件。

5、实施控制

  根据优化求解得到的最优控制输入，最后只取多个输出值中的第一个值实施控制，并将系统状态反馈到模型中，用于下一个时刻的预测和控制。在本案例中，求解代价函数后，得到多个时刻的位置、方向和速度、转向角，只取第一个时刻的值来控制小车，保证车辆跟踪参考轨迹。

三、MPC算法

1、状态空间

  对于离散状态空间表达式
$$x_{k+1}=A{x}_k+B{u}_k$$
其中，系统矩阵 $A$ 为 $n\times n$ 矩阵，输入矩阵 $B$ 为 $n\times p$ 矩阵， $x_k$ 为 $n\times 1$ 矩阵，$u_k$ 为 $p\times 1$ 矩阵。

  在第 $k$ 时刻进行预测，设预测区间为 $N$。为了方便记录，建立两个新的矩阵 $X_k$ 和 $U_k$，分别累计存放每个k所对应的状态量 $x_k$ 和输入量 $u_k$。
$${\mathbf{X}}_k={\left[\begin{array}{c}\mathbf{x}(k|k)\\ \mathbf{x}(k+1|k)\\ \mathbf{x}(k+2|k)\\ ⋮\\ \mathbf{x}(k+N|k)\end{array}\right]}_{(N+1)n\times 1}{\mathbf{U}}_k={\left[\begin{array}{c}\mathbf{u}(k|k)\\ \mathbf{u}(k+1|k)\\ \mathbf{u}(k+2|k)\\ ⋮\\ \mathbf{u}(k+N-1|k)\end{array}\right]}_{Np\times 1}$$
其中，$x(k|k)$ 表示在第 $k$ 时刻对第 $k$ 时刻状态量的预测 ，$x(k+1|k)$ 表示在第 $k$ 时刻对第 $k+1$ 时刻状态量的预测。

  假设系统输出 $y=x$，参考值为 $R=0$，则误差为：
$$E=y-R=x$$

2、代价函数

  定义代价函数为：
$$\mathbf{min}J=\sum _k^{N-1}({\mathbf{E}}_k^T\mathbf{Q}{\mathbf{E}}_k+{\mathbf{u}}_k^T\mathbf{R}{\mathbf{u}}_k)+{\mathbf{E}}_N^T\mathbf{F}{\mathbf{E}}_N$$
即：
$$J=\sum _{i=0}^{N-1}(\begin{array}{c}\underbrace{\mathbf{x}(k+i|k{)}^T\mathbf{Q}\mathbf{x}(k+i|k)}\\ \mathbf{误差加权和}\end{array}+\begin{array}{c}\underbrace{\mathbf{u}(k+i|k{)}^T\mathbf{R}\mathbf{u}(k+i|k)}\\ \mathbf{输入加权和}\end{array})+\begin{array}{c}\underbrace{\mathbf{x}(k+N|k{)}^T\mathbf{F}\mathbf{x}(k+N|k)}\\ \mathbf{终端误差}\end{array}$$
  上式代价函数包含误差加权和、输入加权和以及终端误差三者之和。其中含有未知量 $x$ 和 $u$，由于我们是要对 $u$ 进行优化，所以需要把 $x$ 消去，假设在 $k$ 时刻对 $k$时刻状态量的预测 $x(k|k)$为 $x_k$ ，则 $k$ 时刻对 $k+1$ 时刻状态量的预测 $x(k+1\mid k)$ 可利用状态方程进行化简推导… 然后，我们就可以推导出 $x(k+N\mid k)$ 的表达式。

$$\begin{array}{rl}\mathbf{x}\left(k|k\right)& =x_k\\ \mathbf{x}\left(k+1|k\right)& =\mathbf{Ax}\left(k|k\right)+\mathbf{Bu}\left(k|k\right)={\mathbf{Ax}}_k+\mathbf{Bu}\left(k|k\right)\\ \mathbf{x}\left(k+2|k\right)& =\mathbf{Ax}\left(k+1|k\right)+\mathbf{Bu}\left(k+1|k\right)={\mathbf{A}}^2{\mathbf{x}}_k+\mathbf{ABu}\left(k|k\right)+\mathbf{Bu}\left(k+1|k\right)\\ ⋮& \\ \mathbf{x}\left(k+N|k\right)& ={\mathbf{A}}^N{\mathbf{x}}_k+{\mathbf{A}}^{N-1}\mathbf{Bu}\left(k|k\right)+\cdots +\mathbf{Bu}\left(k+N-1|k\right)\end{array}$$  利用矩阵形式的$X_k$ 和 $U_k$，将其表示成更加简洁的形式 $X_k=M{x}_k+C{U}_k$，即：
$${\mathbf{X}}_k=\left[\begin{array}{c}{\mathbf{I}}_{n\times n}\\ {\mathbf{A}}_{n\times n}\\ {\mathbf{A}}^2\\ ⋮\\ {\mathbf{A}}^N\end{array}\right]{\mathbf{x}}_k+\left[\begin{array}{cccc}{\mathbf{O}}_{n\times 1}& & & \\ {\mathbf{B}}_{n\times p}& & & \\ \mathbf{AB}& \mathbf{B}& & \\ ⋮& ⋮& \ddots & \\ {\mathbf{A}}^{N-1}\mathbf{B}& {\mathbf{A}}^{N-2}\mathbf{B}& \cdots & \mathbf{B}\end{array}\right]{\mathbf{U}}_k$$其中， $M$ 为 $(N+1)n\times n$ 矩阵， $C$ 为 $(N+1)n\times Np$ 矩阵。
  将上式带入代价函数：
$$\begin{array}{rl}& \mathbf{J}=\sum _{i=0}^{N-1}(\mathbf{x}(k+i|k{)}^T\mathbf{Q}\mathbf{x}(k+i|k)+\mathbf{u}(k+i|k{)}^T\mathbf{R}\mathbf{u}(k+i|k))+\mathbf{x}(k+N{)}^T\mathbf{F}\mathbf{x}(k+N)\\ & ={\left[\begin{array}{c}\mathbf{x}(k|k)\\ \mathbf{x}(k+1|k)\\ ⋮\\ \mathbf{x}(k+N|k)\end{array}\right]}^T\left[\begin{array}{cccc}\mathbf{Q}& & & \\ & \mathbf{Q}& & \\ & & \ddots & \\ & & & \mathbf{F}\end{array}\right]\left[\begin{array}{c}\mathbf{x}(k|k)\\ \mathbf{x}(k+1|k)\\ ⋮\\ \mathbf{x}(k+N|k)\end{array}\right]+{\left[\begin{array}{c}\mathbf{u}(k|k)\\ \mathbf{u}(k+1|k)\\ ⋮\\ \mathbf{u}(k+N-1|k)\end{array}\right]}^T\left[\begin{array}{cccc}\mathbf{R}& & & \\ & \mathbf{R}& & \\ & & \ddots & \\ & & & \mathbf{R}\end{array}\right]\left[\begin{array}{c}\mathbf{u}(k|k)\\ \mathbf{u}(k+1|k)\\ ⋮\\ \mathbf{u}(k+N-1|k)\end{array}\right]\end{array}$$
  整理为用 $X_k$ 和 $U_k$ 表示的形式，即：
$$\begin{array}{rl}J& =X_k\bar{Q}{X}_k+U_k^T\bar{R}{U}_k\\ & =(M{\mathbf{x}}_k+{\mathbf{CU}}_k{)}^T\bar{\mathbf{Q}}(M{\mathbf{x}}_k+{\mathbf{CU}}_k)+{\mathbf{U}}_k^T\bar{\mathbf{R}}{\mathbf{U}}_k\\ & =({\mathbf{x}}_k^T{\mathbf{M}}^T+{\mathbf{U}}_k^T{\mathbf{C}}^T)\bar{\mathbf{Q}}(\mathbf{M}{\mathbf{x}}_k+\mathbf{C}{\mathbf{U}}_k)+{\mathbf{U}}_k^T\bar{\mathbf{R}}{\mathbf{U}}_k\\ & ={\mathbf{x}}_k^T{\mathbf{M}}^T\bar{\mathbf{Q}}M{\mathbf{x}}_k+2{\mathbf{x}}_k^T{\mathbf{M}}^T\bar{\mathbf{Q}}\mathbf{C}{\mathbf{U}}_k+{\mathbf{U}}_k^T({\mathbf{C}}^T\bar{\mathbf{Q}}\mathbf{C}+\bar{\mathbf{R}}){\mathbf{U}}_k\\ & =x_k^T\mathbf{G}{x}_k+2{\mathbf{x}}_k^T\mathbf{E}{\mathbf{U}}_k+{\mathbf{U}}_k^T\mathbf{H}{\mathbf{U}}_k\end{array}$$  最终得到目标函数的表达式如下，其中 $x_k$ 为给定的初始状态。
$$J=x_k^{T}G{x}_k+2x_k^{T}E{U}_k+U_k^{T}H{U}_k$$其中，式中的系数矩阵的表达式如下：
$$G=M^T\bar{Q}ME=M^T\bar{Q}CH=C^T\bar{Q}C+\bar{R}$$$\overline{Q}$ 和 $\overline{R}$ 是前面两个系数矩阵的增广形式，如下所示：
$$\overline{Q}=\left[\begin{array}{ccc}Q& \cdots & \\ ⋮& Q& ⋮\\ & \cdots & F\end{array}\right]\overline{R}=\left[\begin{array}{ccc}R& \cdots & \\ ⋮& \ddots & ⋮\\ & \cdots & R\end{array}\right]$$即代价函数 $J$ 可以转化为初始状态 $x_k^{T}G{x}_k$ 和二次规划形式 $2x_k^{T}E{U}_k+U_k^{T}H{U}_k$ 的结合。

3、模型求解

二次规划的标准形式：
$$\underset{x}{\min }\frac{1}{2}{x}^{T}Hx+f^{T}x\text{suchthat}\{\begin{array}{c}A\cdot x\le b,\\ Aeq\cdot x=beq,\\ lb\le x\le ub.\end{array}$$使用二次规划求解器求解，存在两个控制量 $u_k$ 的范围约束，没有等式和不等式的约束
对 $J$ 中的 $2x_k^{T}E{U}_k+U_k^{T}H{U}_k$ 部分变形：
$$\frac{1}{2}\left(U_k^{T}H{U}_k+2x_k^{T}E{U}_k\right)=\frac{1}{2}{U}_k^{T}H{U}_k+f^T{U}_k$$写成二次规划形式为
$$\min \frac{1}{2}{U}^{T}HU+f^{T}Us.t.lb\le U\le ub$$求解得到
$${\mathbf{U}}_k={\left[\begin{array}{c}\mathbf{u}(k|k)\\ \mathbf{u}(k+1|k)\\ \mathbf{u}(k+2|k)\\ ⋮\\ \mathbf{u}(k+N-1|k)\end{array}\right]}_{Np\times 1}$$

4、反馈控制

  将二次规划求解得到的 $U_k$ 中的第一项 $u(k|k)$ 输入到控制对象中，通过传感器再次得到对象的 $3$ 个状态量，再经过模型预测控制滚动优化。

四、基于MPC的控制器设计

1、车辆运动学模型(Model)

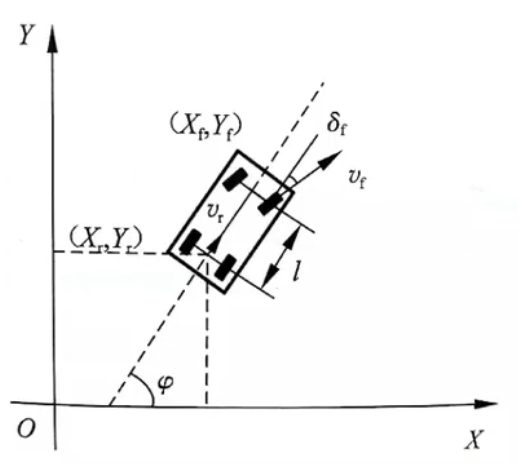
  从运动学模型出发，考虑最简单的情况，只考虑在 $XOY$ 平面坐标系内的运动，如下图所示：

  车辆只包含3个自由度，即水平位移、竖直位移和转动，则车辆的状态(states)为 水平方向坐标$X$ ，竖直方向坐标$Y$ ，车辆航向角 $\phi$. 控制量只有两个：车速 $v$ 和转角 ${\delta }_f$.这里实际上是模拟了真实驾驶的环境，驾驶员只能踩踏板和转动方向盘。
  阿克曼转向车辆的两个前轮转角不同，但两个前轮的垂线与后轮的垂线仍然交于一点，即转向中心，因此可以再简化为自行车模型，后轮速度为 $v_r$ ，前轮速度为 $v_f$。
  对前轮速度沿轴向分解，可得前轮与后轮的速度关系：
$$v_r=v_{f}cos{\delta }_f$$  横向上的速度为：
$$v_y=v_{f}sin{\delta }_f$$   由上两式可得横向上速度与后轮速度的关系为：
$$v_y=v_{r}tan{\delta }_f$$   横向上的速度会引起车辆发生以后轮中心为圆心的圆周运动，因此车辆摆动的角速度为：
$$\omega =\frac{v_y}{l}$$  状态空间方程为：
$$\{\begin{array}{c}\begin{array}{c}\dot{x}=v_r\cos \phi \\ \dot{Y}=v_r\sin \phi \end{array}\\ \dot{\phi }=\frac{v_r\tan {\delta }_f}{l}\end{array}$$

2、模型线性化(Linearization)

  由于非线性的表达式，不能写成矩阵的形式，因此需要对建立的运动学模型进行线性化处理，在参考点处进行泰勒展开近似，进行反馈线性化，目的是要把误差线性化。
用 $\xi$ 表示系统的状态量，用 $\mu$ 表示系统的控制量，则具体形式如下：
$$\xi =\left[\begin{array}{c}x\\ y\\ \phi \end{array}\right]u=\left[\begin{array}{c}{v}_r\\ {\delta }_f\end{array}\right]$$  则系统的状态空间可表示为：
$$\dot{\xi }=f(\xi ,u)$$  要想写为向量和矩阵的形式，即 $\dot{X}=AX+Bu$ ，需要近似线性化，使用泰勒展开式：
$$f\left(x\right)=\frac{f\left(x_0\right)}{0!}+\frac{f^{\prime }\left(x_0\right)}{1!}\left(x-x_0\right)+\frac{f^{\prime \prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+...+\frac{f^{\left(n\right)}\left(x_0\right)}{n!}{\left(x-x_0\right)}^n+R_n(x)$$
  对多元函数的求导就是求雅可比矩阵：
$$J_f(x_1,\cdots ,x_n)=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]$$  要进行泰勒展开，首先看在哪一点进行展开，假设已知参考轨迹 ${\xi }_r=[X_r{Y}_r{\phi }_r{]}^T$
  取一阶泰勒展开形式，在参考点处展开：
$$\dot{\xi }\approx f({\xi }_r,u_r)+\frac{\partial f}{\partial \xi }(\xi -{\xi }_r)+\frac{\partial f}{\partial u}(u-u_r)$$   定义误差为 $\tilde{\xi }=\xi -{\xi }_r$，其导数为 $\dot{\tilde{\xi }}=\dot{\xi }-{\dot{\xi }}_r$，则 ${\dot{\xi }}_r=f({\xi }_r,{\mu }_r)$，还可定义$\widetilde{\mu =\mu -{\mu }_r}$
线性化后的形式为
$$\dot{\tilde{\xi }}=\dot{\xi }-{\dot{\xi }}_r=\frac{\partial f}{\partial \xi }\tilde{\xi }+\frac{\partial f}{\partial \mu }\tilde{\mu }$$则线性状态空间方程为：
$$\dot{\tilde{\xi }}=A\tilde{\xi }+B\tilde{u}$$其中，状态量的误差为
$$\tilde{\xi }=\xi -{\xi }_r=\left[\begin{array}{c}X-X_r\\ Y-Y_r\\ \phi -{\phi }_r\end{array}\right]$$对于输入来讲，其实是没有参考的输入量 $u_r$，只有实际的输入量 $u$，因此：

$$\tilde{u}=u-u_r=\left[\begin{array}{c}{v}_r\\ {\delta }_f\end{array}\right]$$下面求解矩阵 $A$ 和 $B$ ，也就是求解雅克比矩阵：

$$A=\frac{\partial f}{\partial \xi }=\left[\begin{array}{c}\frac{\partial f_1}{\partial {\xi }_1}\frac{\partial f_1}{\partial {\xi }_2}\frac{\partial f_1}{\partial {\xi }_3}\\ \frac{\partial f_2}{\partial {\xi }_1}\frac{\partial f_2}{\partial {\xi }_2}\frac{\partial f_2}{\partial {\xi }_3}\\ \frac{\partial f_3}{\partial {\xi }_1}\frac{\partial f_3}{\partial {\xi }_2}\frac{\partial f_3}{\partial {\xi }_3}\end{array}\right]B=\frac{\partial f}{\partial u}=\left[\begin{array}{c}\frac{\partial f_1}{\partial u_1}\frac{\partial f_1}{\partial u_2}\\ \frac{\partial f_2}{\partial u_1}\frac{\partial f_2}{\partial u_2}\\ \frac{\partial f_3}{\partial u_1}\frac{\partial f_3}{\partial u_2}\end{array}\right]$$其中， $f_1=v_{r}cos{\phi }_r$，$f_2=v_{R}sin{\phi }_r$， $f_3=\frac{v_r\tan {\delta }_f}{L}$，${\xi }_1=X$， ${\xi }_2=Y$， ${\xi }_3=\phi$.注意在哪一点展开，求的就是那一点的导数。
带入求解得:
$$A=\left[\begin{array}{ccc}0& 0& -v_r\sin {\phi }_r\\ 0& 0& v_r\cos {\phi }_r\\ 0& 0& 0\end{array}\right]B=\left[\begin{array}{cc}\cos {\phi }_r& 0\\ \sin {\phi }_r& 0\\ \frac{\tan {\delta }_f}{l}& \frac{v_r}{l{\cos }^2{\delta }_f}\end{array}\right]$$

3、模型离散化(Discretization)

  模型经过线性化后，仍然是一个连续的模型，无法使用递推的MPC运算，因此还需要进行离散化。
  离散化是对模型的进一步近似，使用前向欧拉法(Forward-Euler method)，使用差商代替微分，设采样时间为 $T$ ， 后一个时刻的采样减去前一个时刻的采样，再除以采样时间，近似表示在这一点的导数即：
$$\dot{\xi }=\frac{\tilde{\xi }(k+1)-\xi (k)}{T}=A\tilde{\xi }(k)+B\tilde{\mu }(k)$$移项整理为
$$\begin{array}{rl}\tilde{\xi }\left(k+1\right)& =\left(I+TA\right)\tilde{\xi }\left(k\right)+TB\tilde{u}\left(k\right)\\ & =\tilde{A}\tilde{\xi }\left(k\right)+\tilde{B}\tilde{u}\left(k\right)\end{array}$$其中
$$\tilde{A}=\left[\begin{array}{ccc}1& 0& -T{v}_r\sin {\phi }_r\\ 0& 1& T{v}_r\cos {\phi }_r\\ 0& 0& 1\end{array}\right]\tilde{B}=\left[\begin{array}{cc}T\cos {\phi }_r& 0\\ \begin{array}{c}T\sin {\phi }_r\\ T\frac{\tan {\delta }_f}{l}\end{array}& \begin{array}{c}0\\ \frac{T{v}_r}{l{\cos }^2{\delta }_f}\end{array}\end{array}\right]$$  离散化后的模型可用于设计控制器。

五、编程实现

import numpy as np
import matplotlib
matplotlib.use('TkAgg') # matplotlib切换图形界面显示终端TkAgg
import matplotlib.pyplot as plt
import cvxpy
import math
import sys
 
#一、无人车轨迹跟踪运动学模型
class Vehicle:
    def __init__(self):  # 车辆
        self.x = 0  # 初始x
        self.y = -4  # 初始y
        self.psi = 0  # 初始航向角
        self.v = 2  # 初始速度
        self.av = 1 # 加速度，为0就是恒速；
        self.L = 2 # 车辆轴距，单位：m
        self.dt = 0.1  # 时间间隔，单位：s
        self.R = np.diag([0.1, 0.1])  # [[0.1,0],[0,0.1]]  input cost matrix, 控制区间的输入权重，输入代价矩阵，Ru(k)
        self.Q = np.diag([1, 1, 1])  # state cost matrix 预测区间的状态偏差，给定状态代价矩阵， Qx(k)
        self.Qf = np.diag([1, 1, 1])  # state final matrix = 最终状态代价矩阵
        self.MAX_STEER = np.deg2rad(45.0)  # maximum steering angle [rad] 最大转向角
        self.MAX_VEL = 100.0  # maximum accel [m/s]  最大速度
 
    def update_state(self, delta_f):
        self.x = self.x+self.v*math.cos(self.psi)*self.dt
        self.y = self.y+self.v*math.sin(self.psi)*self.dt
        self.psi = self.psi+self.v/self.L*math.tan(delta_f)*self.dt
        self.v = self.v + self.av * self.dt
 
    def get_state(self):
        return self.x, self.y, self.psi, self.v
 
    def state_space(self, ref_delta, ref_yaw):
        """Args: ref_delta (_type_): 参考的转角控制量;  ref_yaw (_type_): 参考的偏航角 """
        A = np.matrix([
            [1.0, 0.0, -self.v * self.dt*math.sin(ref_yaw)],
            [0.0, 1.0, self.v * self.dt*math.cos(ref_yaw)],
            [0.0, 0.0, 1.0]])
        B = np.matrix([
            [self.dt*math.cos(ref_yaw), 0],
            [self.dt*math.sin(ref_yaw), 0],
            [self.dt*math.tan(ref_delta)/self.L, self.v*self.dt /(self.L*math.cos(ref_delta)*math.cos(ref_delta))]
        ])
        C = np.eye(3)  # 3x3的单位矩阵
        return A, B, C
 
# 二、道路模型，虚拟道路上1000个点，给出每个点的位置（x坐标, y坐标，轨迹点的切线方向, 曲率k）
class VPath:
    def __init__(self, util):
        self.refer_path = np.zeros((1000, 4))
        self.refer_path[:, 0] = np.linspace(0, util.x_xis, 1000)  # x 间隔起始点、终止端，以及指定分隔值总数，x的间距为0.1
        self.refer_path[:, 1] = 2*np.sin(self.refer_path[:, 0]/3.0) + 2.5*np.cos(self.refer_path[:, 0]/2.0)  # y
        # 使用差分的方式计算路径点的一阶导和二阶导，从而得到切线方向和曲率
        for i in range(len(self.refer_path)):
            if i == 0:
                dx = self.refer_path[i+1, 0] - self.refer_path[i, 0]
                dy = self.refer_path[i+1, 1] - self.refer_path[i, 1]
                ddx = self.refer_path[2, 0] + self.refer_path[0, 0] - 2*self.refer_path[1, 0]
                ddy = self.refer_path[2, 1] + self.refer_path[0, 1] - 2*self.refer_path[1, 1]
            elif i == (len(self.refer_path)-1):
                dx = self.refer_path[i, 0] - self.refer_path[i-1, 0]
                dy = self.refer_path[i, 1] - self.refer_path[i-1, 1]
                ddx = self.refer_path[i, 0] + self.refer_path[i-2, 0] - 2*self.refer_path[i-1, 0]
                ddy = self.refer_path[i, 1] + self.refer_path[i-2, 1] - 2*self.refer_path[i-1, 1]
            else:
                dx = self.refer_path[i+1, 0] - self.refer_path[i, 0]
                dy = self.refer_path[i+1, 1] - self.refer_path[i, 1]
                ddx = self.refer_path[i+1, 0] + self.refer_path[i-1, 0] - 2*self.refer_path[i, 0]
                ddy = self.refer_path[i+1, 1] + self.refer_path[i-1, 1] - 2*self.refer_path[i, 1]
            self.refer_path[i, 2] = math.atan2(dy, dx)  # yaw
            self.refer_path[i, 3] = (ddy * dx - ddx * dy) / ((dx ** 2 + dy ** 2)**(3 / 2))  # 曲率k计算
 
# 三、MPC
class MPC:
    def __init__(self):
        self.NX = 3  # 状态x = x, y, yaw = x，y坐标，偏航角
        self.NU = 2  # 输入变量u = [v, delta] = [速度，前轮转角]
        self.T = 8  # horizon length  预测区间=时间范围=8个dt
 
    """找出车辆当前实际位置(x,y)与距离道路最近的点
    返回结果：将计算出的横向误差 e、曲率 k、最近目标位置所在路径段处的航向角yaw 和最近目标位置所在路径段的下标 s
    """
    def calc_track_error(self, util, path, x, y):
        # 计算小车当前位置与参考路径上每个点之间的距离，找到距离小车最近的参考路径点，将该点的下标保存为 s
        d_x = [path.refer_path[i, 0]-x for i in range(len(path.refer_path))]
        d_y = [path.refer_path[i, 1]-y for i in range(len(path.refer_path))]
        d = [np.sqrt(d_x[i]**2+d_y[i]**2) for i in range(len(d_x))]
        s = np.argmin(d)  # 求最小值对应的索引
        yaw = path.refer_path[s, 2]
        k = path.refer_path[s, 3]  # 将参考路径上距离小车最近的点的曲率 k 作为小车所在路径段的曲率
        # 将小车当前位置与距离最近的参考路径点之间的连线,与参考路径在该点处的方向角之差,作为小车当前位置与参考路径之间的方向角误差 angle。
        angle = util.normalize_angle(yaw - math.atan2(d_y[s], d_x[s]))
        e = d[s]  # 将小车当前位置与参考路径上距离最近的点之间的距离作为小车的横向误差 e
        if angle < 0:  # 根据 angle 的符号将横向误差 e 取正或取负：如果 angle 小于 0，则将横向误差 e 取负
            e *= -1
        return k, s
 
    """由当前小车的位置实际值(x,y)，取离道路最近的几个目标值
        参数：robot_state是车辆的当前状态(x,y,yaw,v); 
        返回值：xref=3行9列共九段预测区间的(x,y,yaw), ind=当前路径段的下标, dref=二行八列(v, 前轮转角)
    """
    def calc_ref_trajectory(self, util, vehicle, path, robot_state):
        # 曲率 k、小车所在路径段的下标 s
        k, ind = self.calc_track_error(util, path, robot_state[0], robot_state[1])
        # 初始化参考轨迹：定义一个 3 行 T+1=9 列的数组 xref，用于存储参考轨迹。将第一列的值设为当前小车位置所在路径段的值(x,y,yaw)
        xref = np.zeros((self.NX, self.T + 1))
        ncourse = len(path.refer_path)  # 1000
        # 参考控制量，由车辆轴距和曲率，计算前轮转角
        ref_delta = math.atan2(vehicle.L*k, 1)
        # 二行八列 的第 0 行所有列车速，第 1 行所有列是转角
        dref = np.zeros((self.NU, self.T))
        dref[0, :] = robot_state[3]
        dref[1, :] = ref_delta
        travel = 0.0
        for i in range(self.T + 1):
            if (ind + i) < ncourse:
                xref[0, i] = path.refer_path[ind + i, 0]  # x坐标
                xref[1, i] = path.refer_path[ind + i, 1]  # y坐标
                xref[2, i] = path.refer_path[ind + i, 2]  # yaw
        return xref, ind, dref
 
    """
    通过二次线性规划算法，由几个目标点的状态和控制量，计算未来最优的几个点的状态和控制量
    xref: reference point=shape(3,9)=(x,y,yaw; 0~8)
    x0: initial state，(x,y,yaw), 
    delta_ref: reference steer angle 参考转向角 =(2,8)=(v,转角；0~7 )
    ugv:车辆对象
    mpc控制的代价函数 
        minJ(U)=sum(u^T R u + x^T Q x + x^T Qf x)
    约束条件 
        x(k+1) = Ax(k) + Bu(k) + C
        x(k)=[x-xr, y-yr, yaw-yawr]
        u(k)=[v-vr, delta-deltar]
        x(0)=x0
        u(k)<=umax
    """
    def linear_mpc_control(self, util, vehicle, xref, x0, delta_ref):
        x = cvxpy.Variable((self.NX, self.T + 1))  # 定义状态变量9维向量x，具体数值不确定
        u = cvxpy.Variable((self.NU, self.T))      # 定义控制变量 u=[速度，前轮转角]
        cost = 0.0  # 代价函数
        constraints = []  # 约束条件
        for t in range(self.T):
            cost += cvxpy.quad_form(u[:, t] - delta_ref[:, t], vehicle.R)  # 衡量输入大小=u^T R u
            if t != 0: # 因为x(0)=x0，所以t=0时，x(0)==x0，不需要约束条件
                cost += cvxpy.quad_form(x[:, t] - xref[:, t], vehicle.Q)  # 衡量状态偏差=x^T Q x
            A, B, C = vehicle.state_space(delta_ref[1, t], xref[2, t]) # (转角，偏航角)
            constraints += [x[:, t + 1]-xref[:, t+1] == A @ (x[:, t]-xref[:, t]) + B @ (u[:, t]-delta_ref[:, t])]
        cost += cvxpy.quad_form(x[:, self.T] - xref[:, self.T], vehicle.Qf)  # 衡量最终状态偏差=x^T Qf x
 
        constraints += [(x[:, 0]) == x0]
        constraints += [cvxpy.abs(u[0, :]) <= vehicle.MAX_VEL]
        constraints += [cvxpy.abs(u[1, :]) <= vehicle.MAX_STEER]
        # 定义了一个“问题”，“问题”函数里填写凸优化的目标，目前的目标就是cost最小
        prob = cvxpy.Problem(cvxpy.Minimize(cost), constraints)
        # 求解，运行完这一步才能确定x的具体数值
        prob.solve(solver=cvxpy.ECOS, verbose=False)
        # # prob.value储存的是minimize(cost)的值，就是优化后目标的值; 查看变量x使用x.value
        if prob.status == cvxpy.OPTIMAL or prob.status == cvxpy.OPTIMAL_INACCURATE:
            opt_x = util.get_nparray_from_matrix(x.value[0, :])
            opt_y = util.get_nparray_from_matrix(x.value[1, :])
            opt_yaw = util.get_nparray_from_matrix(x.value[2, :])
            opt_v = util.get_nparray_from_matrix(u.value[0, :])
            opt_delta = util.get_nparray_from_matrix(u.value[1, :])
        else:
            opt_v, opt_delta, opt_x, opt_y, opt_yaw = None, None, None, None, None,
        return opt_v, opt_delta, opt_x, opt_y, opt_yaw
 
# 工具类
class Util:
    def __init__(self):
        self.x_xis = 100  # x轴的长度100,共1000个点
    # 展示动图
    def draw(self, ugv, path, mpc):
        x_ = []
        y_ = []
        fig = plt.figure(1)  # 图像编号1
        plt.pause(4) # 图形会间隔1秒后绘制
        for i in range(sys.maxsize):
            robot_state = np.zeros(4)  # [0, 0, 0, 0]
            robot_state[0] = ugv.x
            robot_state[1] = ugv.y
            robot_state[2] = ugv.psi
            robot_state[3] = ugv.v
            x0 = robot_state[0:3]
            xref, target_ind, dref = mpc.calc_ref_trajectory(self, ugv, path, robot_state)
            opt_v, opt_delta, opt_x, opt_y, opt_yaw = mpc.linear_mpc_control(self, ugv, xref, x0, dref)
            # 速度v与x,y坐标不需要传递，只能按车辆指定的速度来计算
            ugv.update_state(opt_delta[0])
            x_.append(ugv.x)
            y_.append(ugv.y)
 
            plt.cla()  # cla清理当前的axes，以下分别绘制蓝色-.线，红色-线，绿色o点
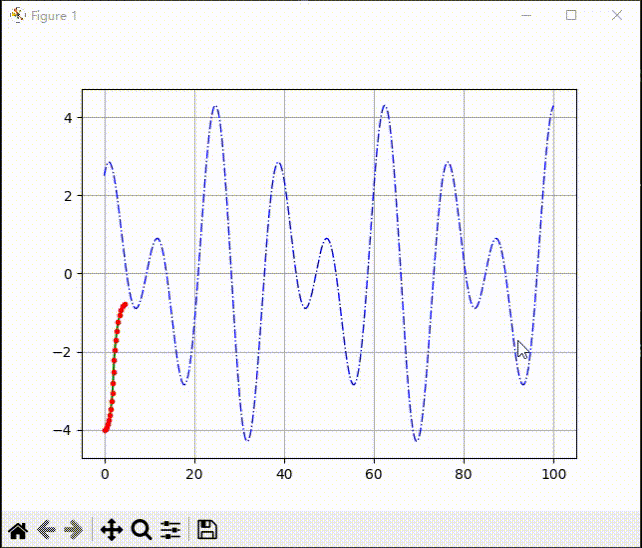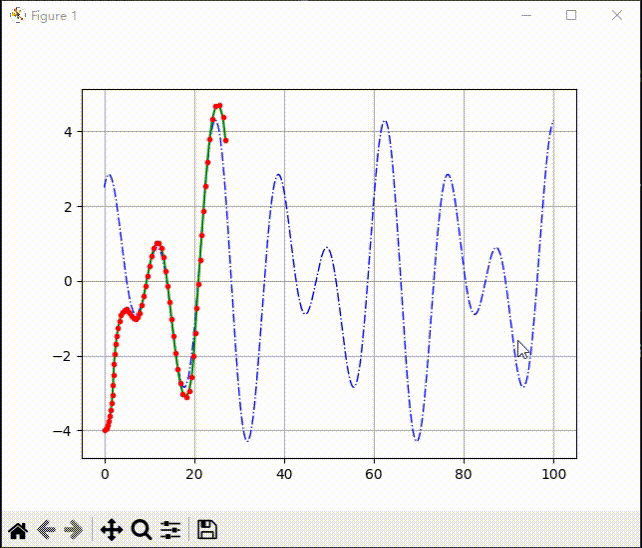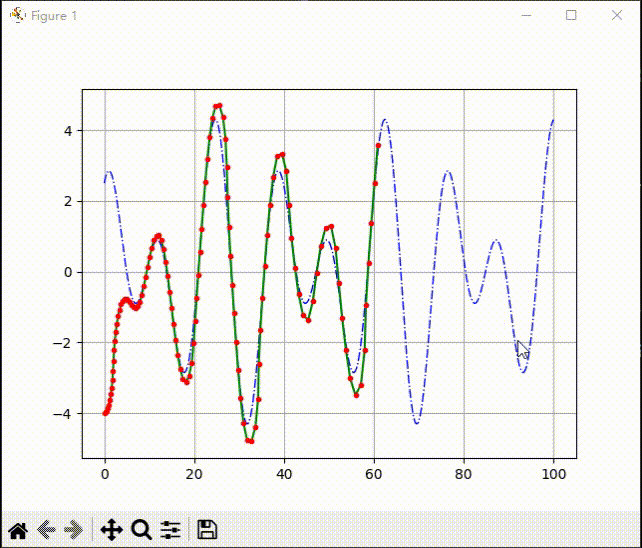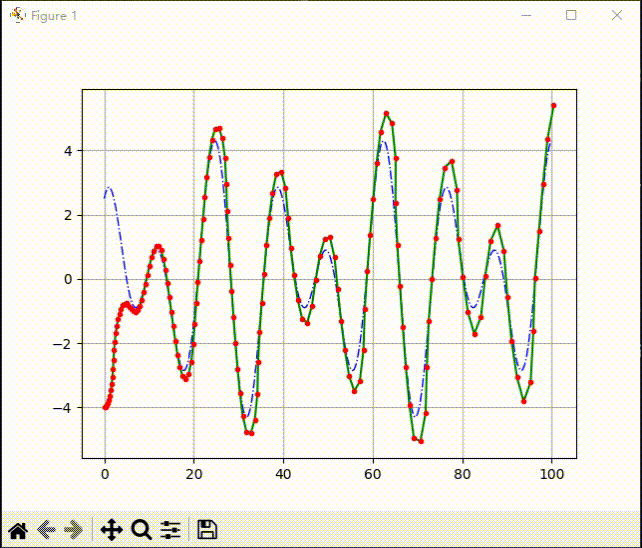
            plt.plot(path.refer_path[:, 0], path.refer_path[:, 1], "-.b",  linewidth=1.0, label="course")
            plt.plot(x_, y_, "-g", label="trajectory")
            plt.plot(x_, y_, ".r", label="target")
            plt.grid(True)  # 显示网格线 1=True=默认显示；0=False=不显示
            plt.pause(0.001) # 图形会间隔0.001秒后重新绘制
            if ugv.x > self.x_xis:  # 判断是否到达最后一个点
                break
        plt.show()  # 在循环结束后显示图像，需要用户手动关闭
 
    # Normalize an angle to [-pi, pi]
    def normalize_angle(self, angle):
        while angle > np.pi:
            angle -= 2.0 * np.pi
        while angle < -np.pi:
            angle += 2.0 * np.pi
        return angle
 
    def get_nparray_from_matrix(self, x):
        return np.array(x).flatten()
 
if __name__=='__main__':
    util = Util()
    ugv = Vehicle()
    path = VPath(util)
    mpc = MPC()
    util.draw(ugv, path, mpc)

效果展示：

参考资料

  1、MPC模型预测控制器学习笔记（附程序）

  2、【控制】模型预测控制 MPC 【合集】Model Predictive Control

  3、你真的把MPC搞懂了吗

  4、模型预测控制（MPC）原理及详细推导

后记：

🌟 感谢您耐心阅读这篇关于 基于运动学模型的车辆轨迹跟踪控制器设计 的技术博客。 📚

🎯 如果您觉得这篇博客对您有所帮助，请不要吝啬您的点赞和评论 📢

🌟您的支持是我继续创作的动力。同时，别忘了收藏本篇博客，以便日后随时查阅。🚀

🚗 让我们一起期待更多的技术分享，共同探索移动机器人的无限可能！💡

🎭感谢您的支持与关注，让我们一起在知识的海洋中砥砺前行 🚀