希尔排序原理

希尔排序（也称为缩小增量排序）采用的是分治的思想，设定一定的间隔，按照这个间隔将集合分成若干个子集合，然后对子集合进行排序；完成后减少这个间隔，再进行排序；逐渐减小这个间隔，直到完成间隔为1的这次排序，即完成集合的排序。
从另一个角度看，希尔排序是插入排序的一个优化。插入排序对于局部有序的集合有更高的排序性能。所以希尔排序前面的缩小间隔过程就是在使集合变得局部有序，最终间隔为1时即为插入排序。

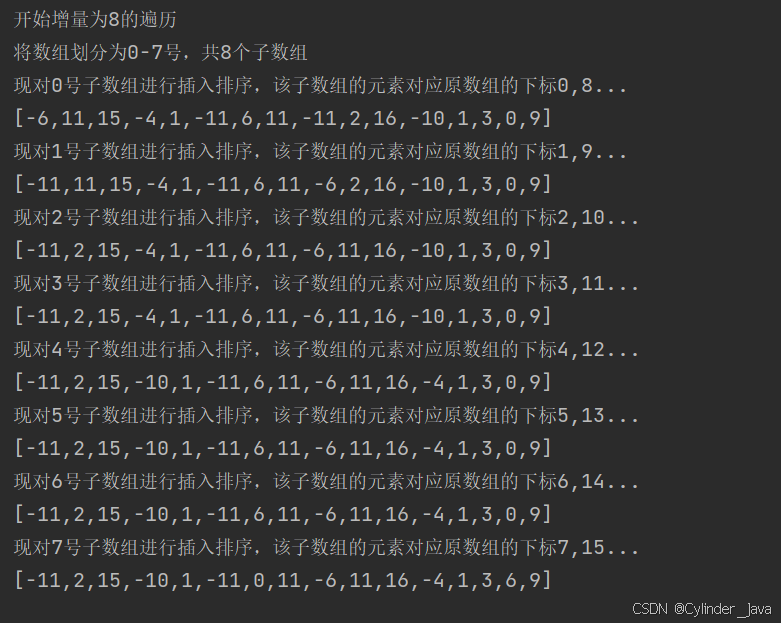
排序演示1

原数组：[-6,11,15,-4,1,-11,6,11,-11,2,16,-10,1,3,0,9]，用希尔排序对这个长度为16的数组进行排序

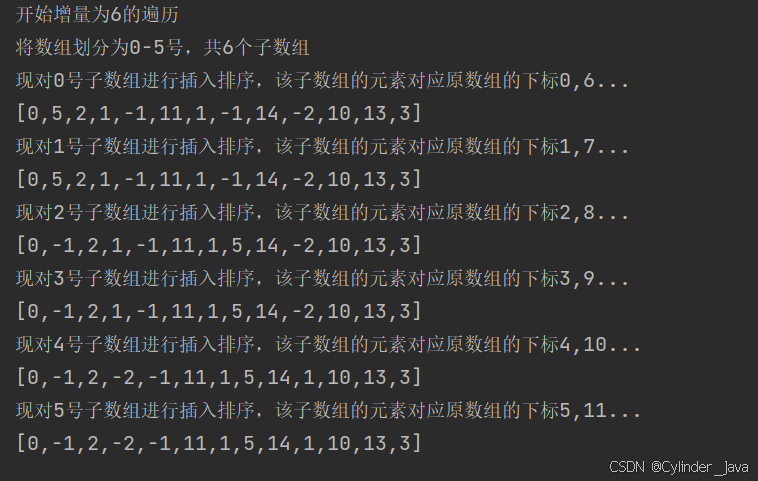
排序演示2

原数组：[0,5,2,1,-1,11,1,-1,14,-2,10,13,3]，用希尔排序对这个长度为13的数组进行排序

复杂度分析

时间复杂度

对于长度为n的集合，为它设置n/2的初始增量，该增量下分出n/2个长度为2或3的子集合，分别对它们进行插入排序；初始增量减半，变为n/2²，该增量下分出n/²个长度为4或5的子集合，分别对它们进行插入排序；继续缩小增量，直到变为1。
对于增量n/2^k的遍历，时间复杂度为：子集合个数n/2^k * 单个子集合进行插入排序的时间O(2^k/n)
增量为1，2，…，n/4，n/2的遍历时间累加，最终的时间复杂度约等于：O(n * log n)。

空间复杂度

排序过程几乎未用到辅助空间，故空间复杂度为：O(1)。

稳定性

排序过程会将不相邻的两个元素交换，有可能打乱两个相同元素之间原有的顺序，故希尔排序是不稳定的。