1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
**进阶:**你可以想出一个时间复杂度小于 O(n^2) 的算法吗?
我最先想到的是暴力求解,题目要求数组中同一个元素在答案里不能重复出现。那么从当前元素下一个开始查找,时间复杂度为O(n^2)
public int[] twoSum(int[] nums, int target) {
int n = nums.length;
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (nums[i] + nums[j] == target) {
return new int[]{i, j};
}
}
}
return new int[0];
}
可以将每次遍历的值按照key为值,value为索引存储在哈希表中,用目标值减去当前值就是我们要找的值,判断哈希表中是否存在该值。哈希表查找元素是常数级别的,所有时间复杂度为O(N)
public int[] twoSum(int[] nums, int target) {
HashMap<Integer, Integer> hashMap = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int temp = target - nums[i];
if(hashMap.containsValue(temp)){
return new int[]{hashMap.get(temp),i};
}
hashMap.put(nums[i],i);
}
return new int[0];
}
2. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
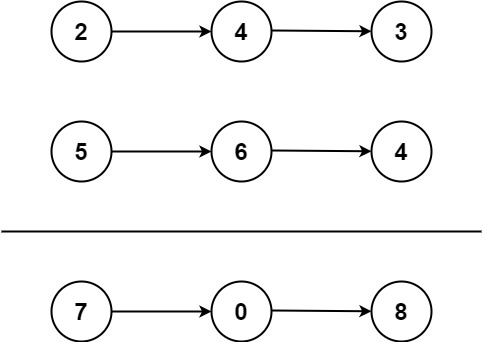
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// // 定义total记录两个数的和
// int total = 0;
// // 定义next记录是否进一
// int next = 0;
// // 定义返回的链表
// ListNode result = new ListNode();
// // 定义一个临时指针
// ListNode cur = result;
//先加到短链表
// while (l1 != null && l2 != null) {
// total = l1.val + l2.val + next;
// cur.next = new ListNode(total % 10);
// next = total / 10;
// l1 = l1.next;
// l2 = l2.next;
// cur = cur.next;
// }
//补全
// while (l1 != null) {
// total = l1.val + next;
// cur.next = new ListNode(total % 10);
// next = total / 10;
// l1 = l1.next;
// cur = cur.next;
// }
// while (l2 != null) {
// total = l2.val + next;
// cur.next = new ListNode(total % 10);
// next = total / 10;
// l2 = l2.next;
// cur = cur.next;
// }
//判断是否还有进位
// if (next != 0) {
// cur.next = new ListNode(next);
// }
// return result.next;
// }
int total = l1.val + l2.val;
int next = total / 10;
ListNode result = new ListNode(total % 10);
if (l1.next != null || l2.next != null || next != 0) {
//如果不为空则按当前值,如果为空补成0
l1 = l1.next = l1.next != null ? l1.next : new ListNode(0);
l2 = l2.next = l2.next != null ? l2.next : new ListNode(0);
l1.val += next;
result.next = addTwoNumbers(l1, l2);
}
return result;
}
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
//滑动窗口
public int lengthOfLongestSubstring(String s) {
int n = s.length();
HashMap<Character, Integer> hashMap = new HashMap<>();
int left = 0;
int res = 0;
for (int i = 0; i < n; i++) {
if (hashMap.containsKey(s.charAt(i))) {
//如果之前已经遇过该字符,取left和hashmap中存取的下标加1的较大者
left = Math.max(left, hashMap.get(s.charAt(i)) + 1);
}
hashMap.put(s.charAt(i), i);
res = Math.max(res, i - left + 1);
}
return res;
}
4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
double res = 0;//结果
int m = nums1.length;
int n = nums2.length;
//特判
if (m == 0 && n == 0) {
return 0;
}
//合并好的数组
int[] arr = new int[m + n];
int q1 = 0;//sum1的索引
int q2 = 0;//sum2的索引
int begin = 0;//新数组的索引
while (q1 < m && q2 < n) {
//如两数相加,能合并到哪先合
if (nums1[q1] <= nums2[q2]) {
arr[begin++] = nums1[q1++];
} else {
arr[begin++] = nums2[q2++];
}
}
//看看是谁已经走完了,num1走完则将num2直接加后面
if (q1 == m) {
while (q2 != n) {
arr[begin++] = nums2[q2++];
}
}
if (q2 == n) {
while (q1 != m) {
arr[begin++] = nums1[q1++];
}
}
//求中位数
int mid = (m + n) / 2;
if ((m + n) % 2 == 0) {
res = (double) (arr[mid] + arr[mid - 1]) / 2;
} else {
res = arr[mid];
}
return res;
}
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
//判断回文的方法
public boolean huiwen(String s) {
int n = s.length();
int l = 0;
int r = n - 1;
while (l < r) {
//从两边向中间走,有一个不同就不是回文
if (s.charAt(l++) != s.charAt(r--)) {
return false;
}
}
return true;
}
public String longestPalindrome(String s) {
int n = s.length();
//特判
if (n < 2) {
return s;
}
//让res初始值为第一个字符
String res = String.valueOf(s.charAt(0));
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) {
String temp = s.substring(i, j + 1);
//这里我必须先判断他是否有资格作为结果(长度要大于之前的结果)
//否则每次都判断是否回文会超时
if (temp.length() > res.length() && huiwen(temp)) {
res = temp;
}
}
}
return res;
}
6. Z 字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"
示例 2:
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入:s = "A", numRows = 1
输出:"A"
提示:
1 <= s.length <= 1000s由英文字母(小写和大写)、','和'.'组成1 <= numRows <= 1000
/**
* 思路:这是一个反转过程
* 例如ABCDEFG 3行
* 0A 1B 2C 开始反转
* 1D 0E 反转
* 1F 2G
* 那么整理 0 1 2对应的字符就是答案
*/
public String convert(String s, int numRows) {
//特判
if (numRows == 1) {
return s;
}
//辅助数组
String[] arr = new String[numRows];
//初始化
for (int i = 0; i < arr.length; i++) {
arr[i]="";
}
int index = 0;//对应思路中的012
int flag = -1;//控制反转
for (int i = 0; i < s.length(); i++) {
//如果index为两端,反转
if (index == 0 || index == numRows - 1) {
flag = -flag;
}
arr[index] += s.charAt(i);
index += flag;
}
String res = "";
//拼接
for (String str : arr) {
res += str;
}
return res;
}
7.整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123
输出:321
示例 2:
输入:x = -123
输出:-321
示例 3:
输入:x = 120
输出:21
示例 4:
输入:x = 0
输出:0
提示:
-231 <= x <= 231 - 1
//主要逻辑:第一位变个位,第二位变十位。。。
public int reverse(int x) {
long res = 0;
while (x != 0) {
int temp = x % 10;
res = res * 10 + temp;
if (res < Integer.MIN_VALUE || res > Integer.MAX_VALUE) {
return 0;
}
x /= 10;
}
return (int) res;
}
//更简便方法,int转stringbuffer,反转后转int
8. 字符串转换整数 (atoi)
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
- 读入字符串并丢弃无用的前导空格
- 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
- 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
- 将前面步骤读入的这些数字转换为整数(即,“123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为
0。必要时更改符号(从步骤 2 开始)。 - 如果整数数超过 32 位有符号整数范围
[−231, 231 − 1],需要截断这个整数,使其保持在这个范围内。具体来说,小于−231的整数应该被固定为−231,大于231 − 1的整数应该被固定为231 − 1。 - 返回整数作为最终结果。
注意:
- 本题中的空白字符只包括空格字符
' '。 - 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
输入:s = "42"
输出:42
解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。
第 1 步:"42"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"42"(读入 "42")
^
解析得到整数 42 。
由于 "42" 在范围 [-231, 231 - 1] 内,最终结果为 42 。
示例 2:
输入:s = " -42"
输出:-42
解释:
第 1 步:" -42"(读入前导空格,但忽视掉)
^
第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数)
^
第 3 步:" -42"(读入 "42")
^
解析得到整数 -42 。
由于 "-42" 在范围 [-231, 231 - 1] 内,最终结果为 -42 。
示例 3:
输入:s = "4193 with words"
输出:4193
解释:
第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止)
^
解析得到整数 4193 。
由于 "4193" 在范围 [-231, 231 - 1] 内,最终结果为 4193 。
提示:
0 <= s.length <= 200s由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-'和'.'组成
public int myAtoi(String s) {
int cur = 0;//字符串索引
int n = s.length();
//特判
if (n == 0) {
return 0;
}
//去除前导空格
while (cur < n && s.charAt(cur) == ' ') {
cur++;
}
int temp = 1;
//去除+-并判断正负
if (cur < n && (s.charAt(cur) == '-' || s.charAt(cur) == '+')) {
if (s.charAt(cur) == '-') {
temp = -1;
cur++;
} else {
cur++;
}
}
int res = 0;
int last = 0;
while (cur < n) {
int num = s.charAt(cur) - '0';//获取当前字符的int值
//如果不是数字则退出
if (num < 0 || num > 9) {
break;
}
last = res;
res = res * 10 + num;
//如果不相等就是溢出了,这道题对于我重点在这
if (last != res / 10) {
return (temp == (-1)) ? Integer.MIN_VALUE : Integer.MAX_VALUE;
}
cur++;
}
return temp * res;
}
9. 回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
- 例如,
121是回文,而123不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
提示:
-231 <= x <= 231 - 1
**进阶:**你能不将整数转为字符串来解决这个问题吗?
public boolean isPalindrome(int x) {
//负数肯定不是回文数
if (x < 0) {
return false;
}
String temp = Integer.toString(x);
int left = 0;
int right = temp.length() - 1;
while (left < right) {
if (temp.charAt(left++) != temp.charAt(right--)) {
return false;
}
}
return true;
}
10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab", p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
提示:
1 <= s.length <= 201 <= p.length <= 30s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。- 保证每次出现字符
*时,前面都匹配到有效的字符
这道题是这十道题里面最难的了,动态规划
public boolean isMatch(String s, String p) {
//特判
if (s == null || p == null) {
return false;
}
int n = s.length();
int m = p.length();
char[] s1 = s.toCharArray();
char[] p1 = p.toCharArray();
//此数组表示s前i个字符能否与p前j个字符匹配
boolean[][] dp = new boolean[n + 1][m + 1];
//初始值,空值匹配空值为true
dp[0][0] = true;
//初始化第一列,此时s的位置是0
for (int j = 1; j < m + 1; j++) {
//情况1:如果p的j-1个位置是’*‘,则j的状态等于j-2的状态
//如:s='',p='a*'
if (p1[j - 1] == '*')
dp[0][j] = dp[0][j - 2];
}
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < m + 1; j++) {
//情况2:如果s和p当前位置相等或者p为'.' dp[i][j]=dp[i-1][j-1]
//如s=“xxxa”,p=xxx."或s="xxxa",p="xxxa"
if (s1[i - 1] == p1[j - 1] || p1[j - 1] == '.')
dp[i][j] = dp[i - 1][j - 1];
else if (p1[j - 1] == '*') {//如果p当前位置为'*'
//情况3:如果s当前位置和p前一个位置一样
//dp[i][j-2]:p向前看了2个位置,相当于*重复了0次 如 s=“xxa” p="xxaa*"
//dp[i][j-1]:p向前看了1个位置,相当于*重复了1次 如 s=“xxa” p="xxa*"
//dp[i-1][j]:s向前看了1个位置,相当于*重复了n次 如 s=“xaa” p="xxa*"
if (s1[i - 1] == p1[j - 2] || p1[j - 2] == '.') {
dp[i][j] = dp[i][j - 2] || dp[i][j - 1] || dp[i - 1][j];
} else {
//情况4:s与p前两个位置不匹配 相当于*重复了0次 如 s=“xxa” p="xxb*"
dp[i][j] = dp[i][j - 2];
}
}
}
}
return dp[n][m];
}