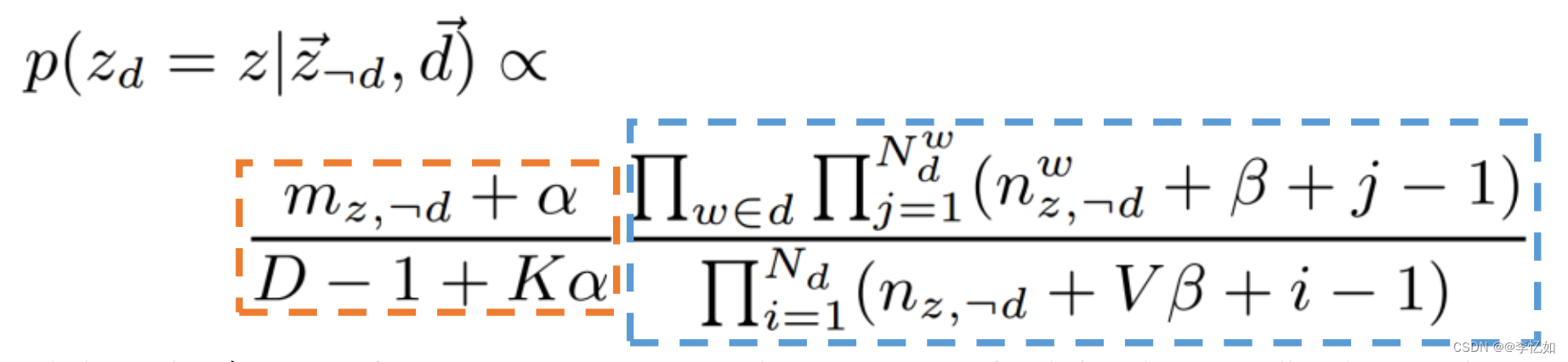目录
系列文章目录
本系列博客重点在自然语言处理NLP的概念原理与代码实践,不包含繁琐的数学推导(有问题欢迎在评论区讨论指出,或直接私信联系我)。
第一章 自然语言处理NLP——GSDMM用于短文本聚类
梗概
本篇博客主要为GSDMM用于短文本聚类的论文导读,进行了论文与算法介绍,并进行了GSDMM模型复现,以及统计结果的分析。(内附数据集与python代码)
论文选择:A Dirichlet Multinomial Mixture Model-based Approach for Short Text Clustering(GSDMM用于短文本聚类)
实验环境:Pycharm2021+scikit-learn0.19.2(避免liner_assignment废除的影响)
一、论文与算法介绍
1.论文背景与简介
随着Twitter等社交媒体的普及,短文聚类已经成为一项越来越重要的任务。这是一个具有挑战性的问题,因为它具有稀疏、高维和大体积的特点。在论文中,作者提出了一种狄利克雷多项式混合模型(缩写为GSDMM)。
我们发现,GSDMM可以自动推断出聚类的数量,并在完整性和稳定性之间取得良好的平衡。而且收敛速度快。也能应对短文的稀疏和高维问题,并能获得每个聚类的代表词。我们广泛的实验研究表明GSDMM的性能明显优于其他三种聚类模型(K-means、HAC、DMAFP),实验所用数据集为Google新闻数据集和Tweet数据集。
2.电影分组过程模拟GSDMM聚类
GSDMM采用类比的方法——通过电影分组过程(MGP)模拟聚类过程。短文本聚类问题可以看作通过每个学生看过的电影清单将学生分组的问题,自然的每一组的学生看的电影(清单)是类似的,而不同组的学生的电影清单差异性是极大的。MGP的类比短文本聚类的内容如表1,电影分组过程(MGP)如表2:
表1 MGP与短文本聚类的类比对应
| MGP | 短文本聚类 |
| 所有学生 | 数据集、语料库 |
| 每个学生、每个电影清单 | 每篇文档 |
| 学生看过的电影、电影清单上的电影 | 文档中的单词 |
表2电影分组过程
| 1. 预定义K个组,将学生随机分配到这K个组中 |
| 2. 针对每一个学生,根据以下准则重新分配分组: a. 选择学生更多的小组 b. 选择电影清单更相似的小组 |
| 3. 将第2步反复进行,直至保留下的组趋于稳定 |
分析:GSDMM的完备性和一致性分别在准则a和准则b上得到体现,准则a让族簇的完备性更强,即让同一个小组尽可能多的包含属于该小组的学生,而准则b让族簇的一致性更强,即让有着同样电影清单的学生尽可能的在一个小组中。
GSDMM通过图1的条件概率进行每个学生的所属的小组的重新分配:
图1 重新分配的条件概率公式
Tips:上面的条件概率公式中橙色虚线框(左边虚线框)中的部分对应准则a,蓝色虚线框(右边虚线框)中的部分对应准则b。
3.算法模型与流程
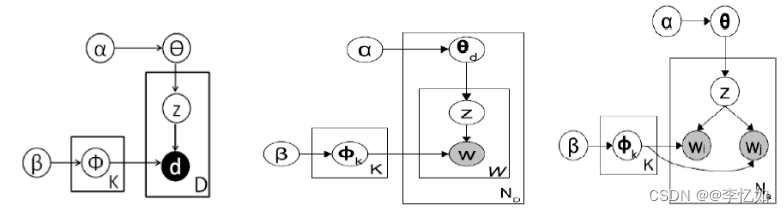
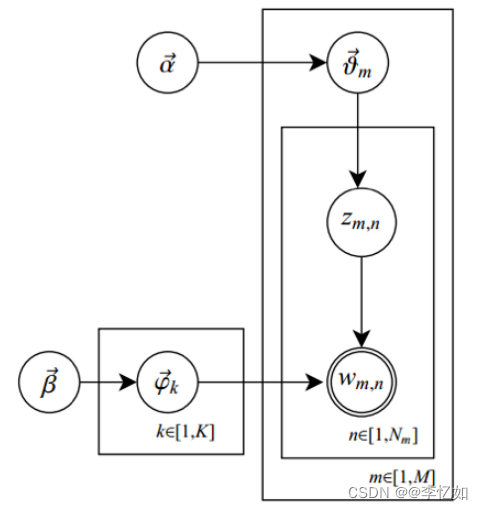
DMM算法模型及与其他模型(LDA、BTM)概率图对比如图2所示:
图2 不同算法模型概率图比较
分析:DMM模型可以看到比LDA少了一层,LDA是主题是先生成文档的主题分布,然后生成每个单词对应的主题,然后根据主题词分布抽取该单词;而DMM是首先生成一个全局主题分布,然后生成文档的主题,每篇文档对应一个主题,再去根据文档的主题抽取文档对应的所有单词;而BTM则是根据文档的单词构造词对,然后抽词对对应的主题。
GSDMM的算法流程如表3所示:
表3 GSDMM算法流程
GSDMM短文本聚类实际流程如下:
1. 假设在初始阶段,我们将文档分类的个数指定为K, 根据文献当中表示,在实验中,这个K值通常比实际类的个数要大。
2. 对于每一篇文档,用d表示,对d进行分类的概率服从多项式分布,比如将d分类到标签为z的族,更新该族的文档数、字数和每个字的出现次数的统计结果,也就是在原来的基础上,文档数+1,字数加上文档d的字数,该类每个字的统计结果加上d对应字的统计信息。
3. 在分类完成后,对下面操作进行迭代:
对于每篇文档,同样用d表示,记录它所分类的标签z1, 在该类z1中剔除文档d,更新z1的相关参数 那么就该重新为d指定一个类了,此时分类的概率服从以标签z1剔除d和d为先验条件的条件概率分布。这其实就是一个吉布斯采样的过程,重新指定类的标签z2, 更新相关的参数。
4.论文结果与分析
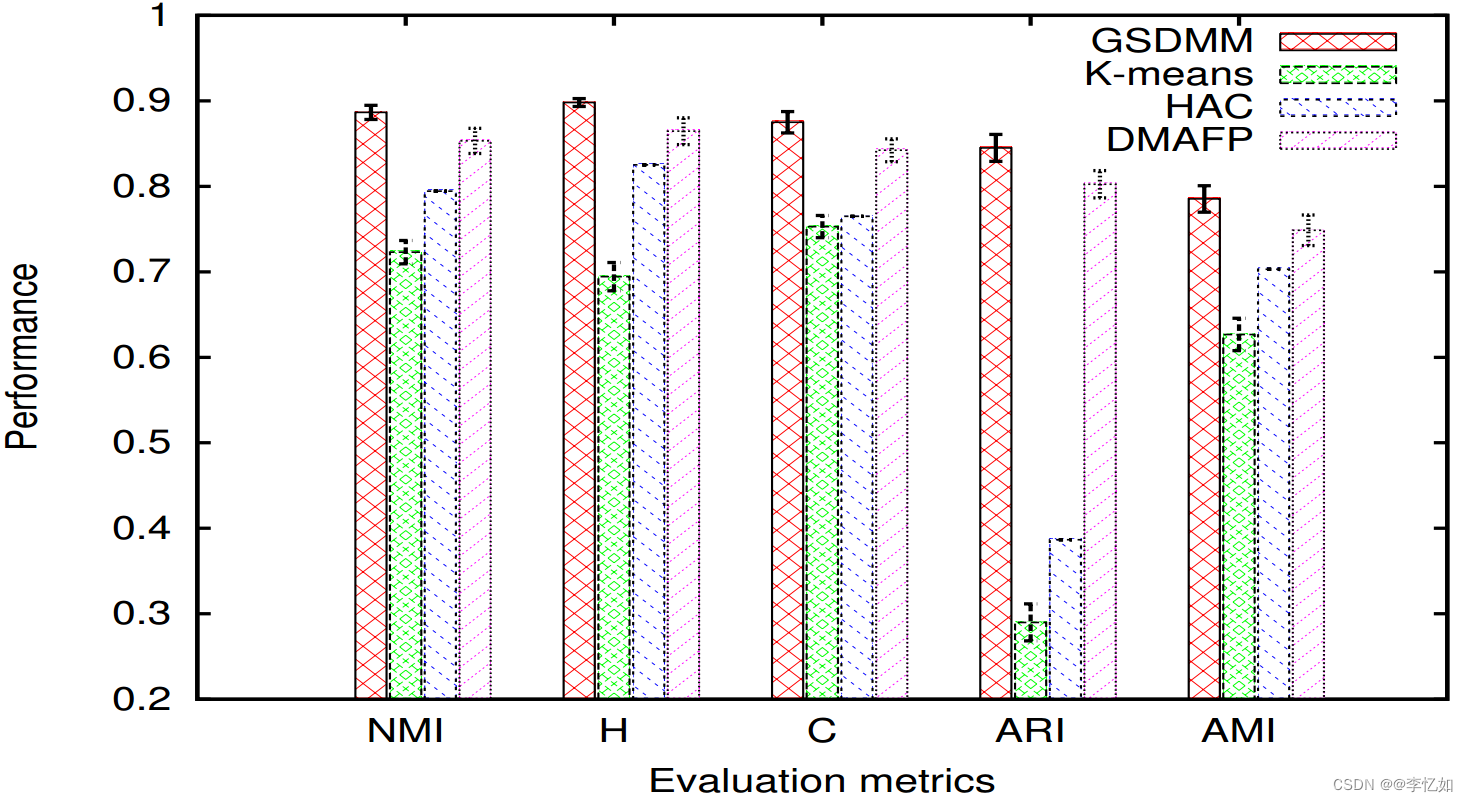
论文中使用GDSMM与K-means、HAC、DMAFP四种聚类模型分别在Google新闻数据集和Tweet数据集上进行实验,以NMI、H、C、ARI、AMI五种聚类标准多维比较了不同聚类模型的聚类效果,结果如图3所示(以TweetSet数据集为例):
图3 不同聚类模型在不同聚类指标下的效果对比
Tips: 基于数据可视化考虑,性能表现基于不同的评价度量方式进行了归一化处理。
分析:由图3可见,GSDMM在不同聚类指标下的性能及效果(Performance)均优于其他三种聚类模型,验证了其在短文本聚类中算法效果的优越性。
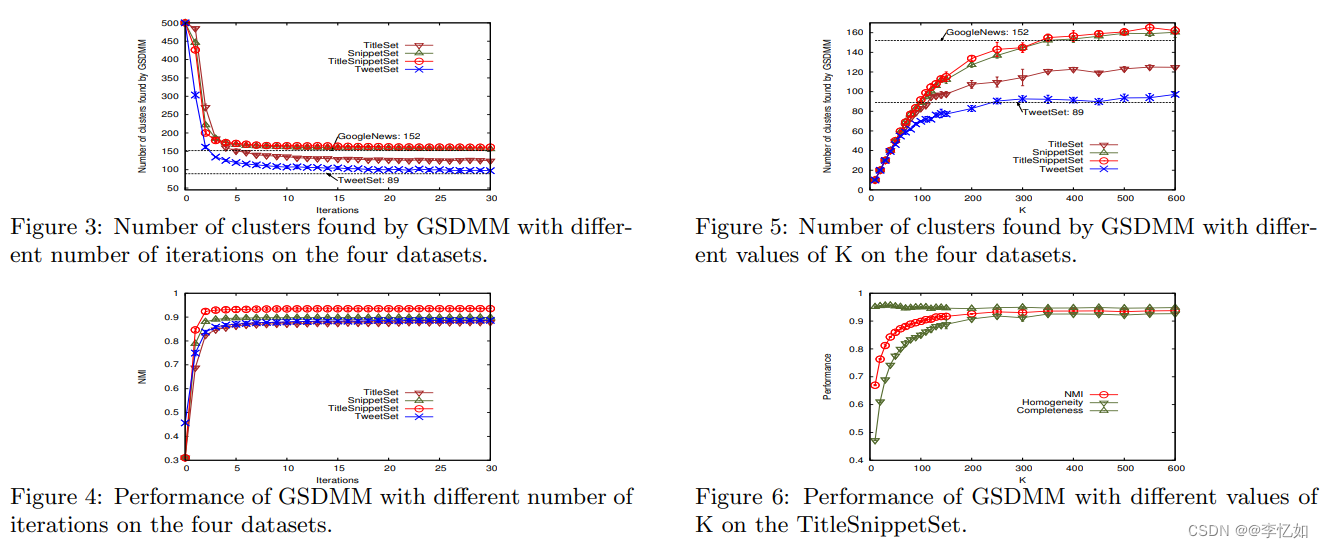
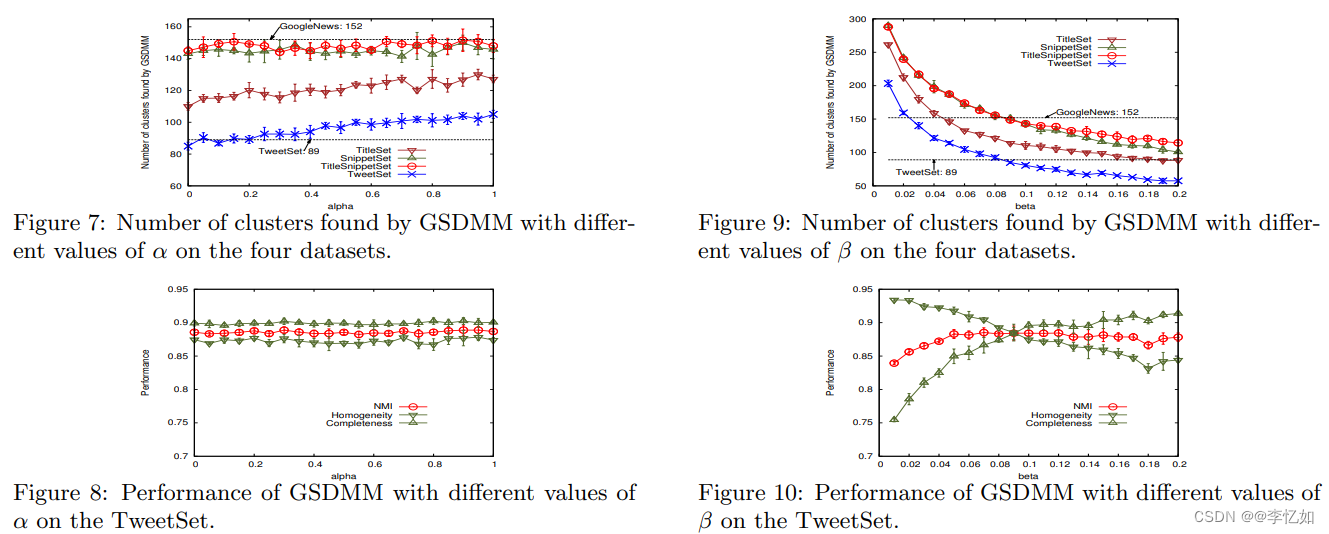
此外,论文中还探究了不同参数情况下聚类效果的对比。其中,不同K与迭代次数对不同数据集结果的影响如图4所示,不同α与β对不同数据集结果的影响如图5所示:
图4 不同K与迭代次数对不同数据集结果的影响
图5 不同α与β对不同数据集结果的影响
分析:由图4与图5可见,这四个参数对于聚类效果的好坏有较大影响。对于数据集TweetSet,由图可知初始族簇大小K值趋于300左右时,参数Alpha等于0.1时,Beta等于0.08时,迭代次数为20次时,GSDMM的聚类结果趋于平稳且效果基本与实际相符。
补充:上述GSDMM的四个参数为经验参数,对于不同的数据集(各个数据集差异较大)最佳的参数取值也会不同。在实际应用中,当给定较好的经验参数,GSDMM具备较好的聚类效果,这使得它具备较高的应用价值。
二、GSDMM模型复现(MGP过程)
1.核心思想
本部分主要通过手写代码对一(2)中的电影分组过程模拟GSDMM过程聚类进行复现,问题及条件如下:
一开始,所有学生随机分配到k个组中,并写下自己最喜欢的电影列表,然后教授来依次读每个人的列表,每个人被读了以后,都要更新组号,满足下面一个或两个条件:
1.新组有更多的学生
2.新组的学生与自己的列表更加相似
不断重复以上操作至所有学生的组号不改变时,就得到我们需要的分组结果了。
实现核心:编写MovieGroupProcess类,构造方法传入对应参数,所需参数如表4:
表4 MGP过程所需核心参数
| 参数 | 作用或定义 |
| K | 聚类个数上限 |
| α | 用于控制学生选当前空的组的概率,当其为0时表示没有人会加入空组 |
| β | 用于控制学生与其他学生相似兴趣的相似度,当其较低时表示学生更渴望与相似兴趣的学生一组,而非更加受欢迎的组 |
| n_iters | 迭代次数 |
2.实现过程
源码地址:GitHub - rwalk/gsdmm: GSDMM: Short text clustering
按照一中的算法流程与模型及二(1)中的核心思想去编写代码实现MGP过程,代码如下:
from numpy.random import multinomial
from numpy import log, exp
from numpy import argmax
import json
class MovieGroupProcess:
def __init__(self, K=8, alpha=0.1, beta=0.1, n_iters=30):
self.K = K
self.alpha = alpha
self.beta = beta
self.n_iters = n_iters
# slots for computed variables
self.number_docs = None
self.vocab_size = None
self.cluster_doc_count = [0 for _ in range(K)]
self.cluster_word_count = [0 for _ in range(K)]
self.cluster_word_distribution = [{} for i in range(K)]
@staticmethod
def from_data(K, alpha, beta, D, vocab_size, cluster_doc_count, cluster_word_count, cluster_word_distribution):
'''
Reconstitute a MovieGroupProcess from previously fit data
:param K:
:param alpha:
:param beta:
:param D:
:param vocab_size:
:param cluster_doc_count:
:param cluster_word_count:
:param cluster_word_distribution:
:return:
'''
mgp = MovieGroupProcess(K, alpha, beta, n_iters=30)
mgp.number_docs = D
mgp.vocab_size = vocab_size
mgp.cluster_doc_count = cluster_doc_count
mgp.cluster_word_count = cluster_word_count
mgp.cluster_word_distribution = cluster_word_distribution
return mgp
@staticmethod
def _sample(p):
'''
Sample with probability vector p from a multinomial distribution
:param p: list
List of probabilities representing probability vector for the multinomial distribution
:return: int
index of randomly selected output
'''
return [i for i, entry in enumerate(multinomial(1, p)) if entry != 0][0]
def fit(self, docs, vocab_size):
'''
Cluster the input documents
:param docs: list of list
list of lists containing the unique token set of each document
:param V: total vocabulary size for each document
:return: list of length len(doc)
cluster label for each document
'''
alpha, beta, K, n_iters, V = self.alpha, self.beta, self.K, self.n_iters, vocab_size
D = len(docs)
self.number_docs = D
self.vocab_size = vocab_size
# unpack to easy var names
m_z, n_z, n_z_w = self.cluster_doc_count, self.cluster_word_count, self.cluster_word_distribution
cluster_count = K
d_z = [None for i in range(len(docs))]
# initialize the clusters
for i, doc in enumerate(docs):
# choose a random initial cluster for the doc
z = self._sample([1.0 / K for _ in range(K)])
d_z[i] = z
m_z[z] += 1
n_z[z] += len(doc)
for word in doc:
if word not in n_z_w[z]:
n_z_w[z][word] = 0
n_z_w[z][word] += 1
for _iter in range(n_iters):
total_transfers = 0
for i, doc in enumerate(docs):
# remove the doc from it's current cluster
z_old = d_z[i]
m_z[z_old] -= 1
n_z[z_old] -= len(doc)
for word in doc:
n_z_w[z_old][word] -= 1
# compact dictionary to save space
if n_z_w[z_old][word] == 0:
del n_z_w[z_old][word]
# draw sample from distribution to find new cluster
p = self.score(doc)
z_new = self._sample(p)
# transfer doc to the new cluster
if z_new != z_old:
total_transfers += 1
d_z[i] = z_new
m_z[z_new] += 1
n_z[z_new] += len(doc)
for word in doc:
if word not in n_z_w[z_new]:
n_z_w[z_new][word] = 0
n_z_w[z_new][word] += 1
cluster_count_new = sum([1 for v in m_z if v > 0])
print("In stage %d: transferred %d clusters with %d clusters populated" % (
_iter, total_transfers, cluster_count_new))
if total_transfers == 0 and cluster_count_new == cluster_count and _iter>25:
print("Converged. Breaking out.")
break
cluster_count = cluster_count_new
self.cluster_word_distribution = n_z_w
return d_z
def score(self, doc):
'''
Score a document
Implements formula (3) of Yin and Wang 2014.
http://dbgroup.cs.tsinghua.edu.cn/wangjy/papers/KDD14-GSDMM.pdf
:param doc: list[str]: The doc token stream
:return: list[float]: A length K probability vector where each component represents
the probability of the document appearing in a particular cluster
'''
alpha, beta, K, V, D = self.alpha, self.beta, self.K, self.vocab_size, self.number_docs
m_z, n_z, n_z_w = self.cluster_doc_count, self.cluster_word_count, self.cluster_word_distribution
p = [0 for _ in range(K)]
# We break the formula into the following pieces
# p = N1*N2/(D1*D2) = exp(lN1 - lD1 + lN2 - lD2)
# lN1 = log(m_z[z] + alpha)
# lN2 = log(D - 1 + K*alpha)
# lN2 = log(product(n_z_w[w] + beta)) = sum(log(n_z_w[w] + beta))
# lD2 = log(product(n_z[d] + V*beta + i -1)) = sum(log(n_z[d] + V*beta + i -1))
lD1 = log(D - 1 + K * alpha)
doc_size = len(doc)
for label in range(K):
lN1 = log(m_z[label] + alpha)
lN2 = 0
lD2 = 0
for word in doc:
lN2 += log(n_z_w[label].get(word, 0) + beta)
for j in range(1, doc_size +1):
lD2 += log(n_z[label] + V * beta + j - 1)
p[label] = exp(lN1 - lD1 + lN2 - lD2)
# normalize the probability vector
pnorm = sum(p)
pnorm = pnorm if pnorm>0 else 1
return [pp/pnorm for pp in p]
def choose_best_label(self, doc):
'''
Choose the highest probability label for the input document
:param doc: list[str]: The doc token stream
:return:
'''
p = self.score(doc)
return argmax(p),max(p)
Tips:在MovieGroupProcess类(MGP过程)中最重要的函数为fit函数,用于对输入文件的聚类的实现。
3.代码测试及结果分析
3.1 测试代码
在定义好MovieGroupProcess类后,需要编写测试代码来测试及验证GSDMM的正确性与聚类效果,测试代码如下(包含字符、词语、短文本聚类):
from unittest import TestCase
from gsdmm.mgp import MovieGroupProcess
import numpy
class TestGSDMM(TestCase):
'''This class tests the Panel data structures needed to support the RSK model'''
def setUp(self):
numpy.random.seed(47)
def tearDown(self):
numpy.random.seed(None)
def compute_V(self, texts):
V = set()
for text in texts:
for word in text:
V.add(word)
return len(V)
def test_grades(self):
grades = list(map(list, [
"A",
"A",
"A",
"B",
"B",
"B",
"B",
"C",
"C",
"C",
"C",
"C",
"C",
"C",
"C",
"C",
"C",
"D",
"D",
"F",
"F",
"P",
"W"
]))
grades = grades + grades + grades + grades + grades
mgp = MovieGroupProcess(K=100, n_iters=100, alpha=0.001, beta=0.01)
y = mgp.fit(grades, self.compute_V(grades))
self.assertEqual(len(set(y)), 7)
for words in mgp.cluster_word_distribution:
self.assertTrue(len(words) in {0, 1}, "More than one grade ended up in a cluster!")
def test_simple_example(self):
# example from @spattanayak1
docs = [['house',
'burning',
'need',
'fire',
'truck',
'ml',
'hindu',
'response',
'christian',
'conversion',
'alm']]
mgp = MovieGroupProcess(K=10, alpha=0.1, beta=0.1, n_iters=30)
vocab = set(x for doc in docs for x in doc)
n_terms = len(vocab)
n_docs = len(docs)
y = mgp.fit(docs, n_terms)
def test_short_text(self):
# there is no perfect segmentation of this text data:
texts = [
"where the red dog lives",
"red dog lives in the house",
"blue cat eats mice",
"monkeys hate cat but love trees",
"green cat eats mice",
"orange elephant never forgets",
"orange elephant must forget",
"monkeys eat banana",
"monkeys live in trees",
"elephant",
"cat",
"dog",
"monkeys"
]
texts = [text.split() for text in texts]
V = self.compute_V(texts)
mgp = MovieGroupProcess(K=30, n_iters=100, alpha=0.2, beta=0.01)
y = mgp.fit(texts, V)
self.assertTrue(len(set(y)) < 10)
self.assertTrue(len(set(y)) > 3)
3.2 聚类
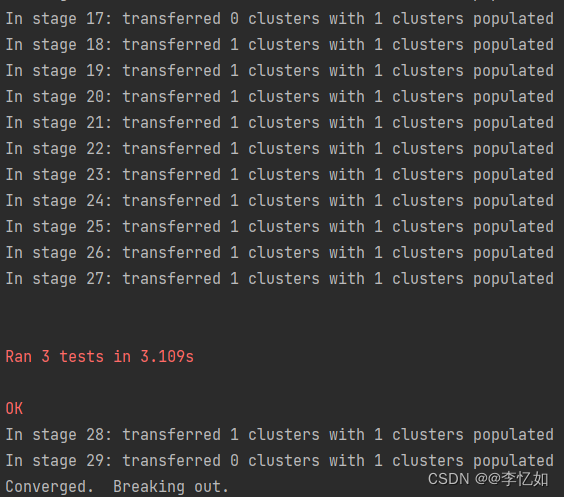
运行测试代码,结果如图6所示:
图6 MGP过程聚类结果
分析:由图6可见,测试代码成功在3.109s内完成了MGP过程,实现了聚类,验证了GSDMM复现的正确性与性能相对优越性,在后文中会在论文数据集下与其他聚类模型进行对比更科学地验证其优势。
三、论文实验复现
本部分主要是对论文实验进行复现,通过NMI、ACC等聚类指标比较GSDMM与其他聚类模型在Tweet数据集下的聚类效果来熟悉GSDMM的实际短文聚类流程与代码,并验证GSDMM的算法优越性,代码与数据集地址如下:
1.项目导入
在github上获取代码后,原代码为Jupyter Notebook代码(.ipynb格式),有以下两种方式导入与运行代码:
1.1 直接使用jupyter
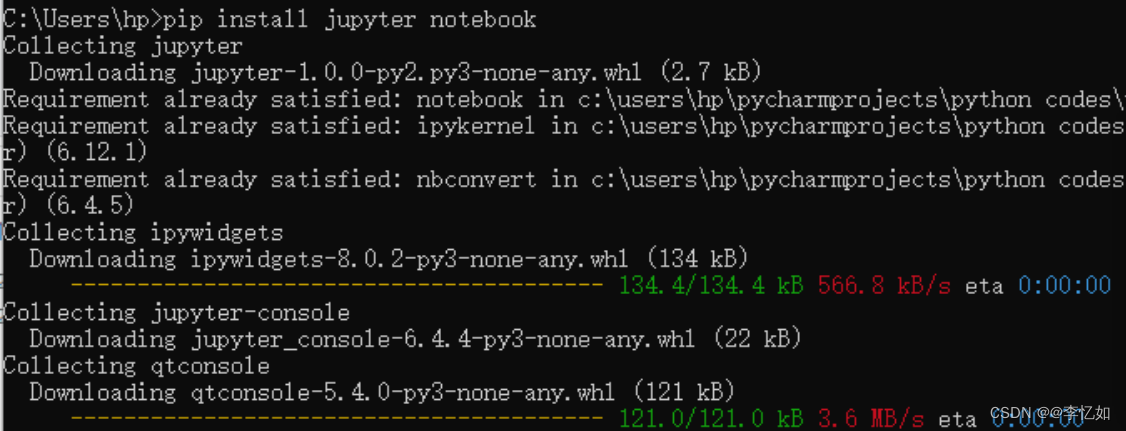
打开cmd,使用pip install notebook命令安装jupyter,过程如图7所示。然后输入jupyter notebook建立连接,在其中upload对应文件后点击Tweet_gsdmm.ipynb即可进入运行界面,如图8所示:
图7 jupyter安装
图8 Jupyter Notebook运行界面
1.2 文件转换使用Pycharm(本实验使用方法)
打开cmd,使用cd命令进入代码项目文件夹,使用jupyter nbconvert --to script *.ipynb命令将ipynb文件转化为py文件,然后将项目导入Pycharm即可。
2.代码及解析
在Pycharm中打开项目,对代码进行解析,核心部分分析如下:
2.1 MovieGroupProcess类的定义
与二中的MGP的类定义类似,定义了相关参数以及数据读入的方式,代码与上文相同。
2.2 分类器的定义
代码第二部分主要是对分类器的定义,包括向量的初始化,训练、评估与预测函数的定义,以及分词训练评估的定义,代码如下:
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import MultiLabelBinarizer
from sklearn.metrics import f1_score
from sklearn.metrics import accuracy_score
import numpy as np
import numpy
class Classifier(object):
def __init__(self, vectors, clf):
self.embeddings = vectors
self.clf = TopKRanker(clf)
self.binarizer = MultiLabelBinarizer(sparse_output=True)
def train(self, X, Y, Y_all):
self.binarizer.fit(Y_all)
X_train = [self.embeddings[int(x)] for x in X]
Y = self.binarizer.transform(Y)
self.clf.fit(X_train, Y)
def evaluate(self, X, Y):
top_k_list = [len(l) for l in Y]
Y_ = self.predict(X, top_k_list)
Y = self.binarizer.transform(Y)
averages = ["micro", "macro", "samples", "weighted"]
results = {}
for average in averages:
results[average] = f1_score(Y, Y_, average=average)
results['accuracy'] = accuracy_score(Y, Y_)
return results
def predict(self, X, top_k_list):
X_ = numpy.asarray([self.embeddings[int(x)] for x in X])
Y = self.clf.predict(X_, top_k_list=top_k_list)
return Y
def split_train_evaluate(self, X, Y, train_precent, seed=0):
state = numpy.random.get_state()
training_size = int(train_precent * len(X))
numpy.random.seed(seed)
shuffle_indices = numpy.random.permutation(numpy.arange(len(X)))
X_train = [X[shuffle_indices[i]] for i in range(training_size)]
Y_train = [Y[shuffle_indices[i]] for i in range(training_size)]
X_test = [X[shuffle_indices[i]] for i in range(training_size, len(X))]
Y_test = [Y[shuffle_indices[i]] for i in range(training_size, len(X))]
self.train(X_train, Y_train, Y)
numpy.random.set_state(state)
return self.evaluate(X_test, Y_test)
from sklearn.multiclass import OneVsRestClassifier
class TopKRanker(OneVsRestClassifier):
def predict(self, X, top_k_list):
probs = numpy.asarray(super(TopKRanker, self).predict_proba(X))
all_labels = []
for i, k in enumerate(top_k_list):
probs_ = probs[i, :]
labels = self.classes_[probs_.argsort()[-k:]].tolist()
probs_[:] = 0
probs_[labels] = 1
all_labels.append(probs_)
return numpy.asarray(all_labels)
2.3 数据的导入与设置
设置好数据集的data_path,可以使用with open进行文件的导入,并使用split进行分词及其相关设置,代码如下:
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from time import time
import re
import numpy as np
from sklearn.metrics.cluster import normalized_mutual_info_score
filename = "Tweet"
# filename = "T"
# filename = "S"
# filename = "TS"
data_path = "./data/" + filename
data = []
docs = []
total_doc_num = 2472
doc_num = 0
doc_label = np.zeros((total_doc_num,), dtype=int)
with open(data_path, 'r')as file:
punc = '",:'
lines = file.readlines()
for line in lines:
line = re.sub(r'[{}]+'.format(punc), '', line)
data.append(" ".join(line.split(' ')[1:-2]))
doc_label[doc_num] = int(line.split(' ')[-1].strip().replace("}", ""))
docs.append(line.split(' ')[1:-2])
doc_num += 1
file.close()
# In[4]:
uni_set = set()
for count in data:
for j in count.split(" "):
uni_set.add(j)
2.4 聚类
在完成MovieGroupProcess类与分类器的定义以及数据导入后,即可进行聚类分析,本实验以ACC与NMI作为聚类指标,其中ACC定义在代码,NMI的计算使用from sklearn.metrics.cluster import normalized_mutual_info_score。聚类参数设置(以K=n_cluster, alpha=0.1, beta=beta, n_iters=10为例)与聚类过程(fit函数搭配分类器)代码如下:
from sklearn.utils.linear_assignment_ import linear_assignment
# from scipy.optimize import linear_sum_assignment as linear_assignment # 添加as语句不用修改代码中的函数名
def acc(y_true, y_pred):
y_true = y_true.astype(np.int64)
assert y_pred.size == y_true.size
D = max(y_pred.max(), y_true.max()) + 1
w = np.zeros((D, D), dtype=np.int64)
for i in range(y_pred.size):
w[y_pred[i], y_true[i]] += 1
ind = linear_assignment(w.max() - w)
return sum([w[i, j] for i, j in ind]) * 1.0 / y_pred.size
# In[6]:
n_cluster = 89
beta = 0.1
mgp = MovieGroupProcess(K=n_cluster, alpha=0.1, beta=beta, n_iters=10)
y = mgp.fit(docs, len(uni_set))
# In[7]:
mgp_doc_label = np.zeros((total_doc_num,), dtype=int)
for i in range(len(docs)):
mgp_doc_label[i] = mgp.choose_best_label(docs[i])[0]
# In[8]:
print("NMI_GSDMM=", normalized_mutual_info_score(np.array(doc_label), np.array(mgp_doc_label)))
print("ACC_GSDMM=", acc(np.array(doc_label), np.array(mgp_doc_label)))
2.5 K-means聚类
按上文方法重新导入与设置数据,并使用不同聚类模型去对Tweet数据集进行聚类,以K-means为例,通过from sklearn.cluster import KMeans导入方法,聚类及统计分析代码如下:
filename = "./data/Tweet_dictionary.txt"
word_id = {}
with open(filename, 'r')as datafile:
sents = datafile.readlines()
for data in sents:
word_id[data.split(" ")[0]] = int(data.split(" ")[1].strip())
datafile.close()
# In[10]:
beta = 0.001
topic_word_dis = np.zeros((n_cluster, len(uni_set)))
for i in range(len(mgp.cluster_word_distribution)):
for j, keyword in enumerate(word_id):
if keyword not in mgp.cluster_word_distribution[i]:
topic_word_dis[i][j] = beta
else:
topic_word_dis[i][j] = mgp.cluster_word_distribution[i][keyword] + beta
# In[11]:
norm_topic_word_dis = topic_word_dis / np.sum(topic_word_dis, axis=1)[:, np.newaxis]
# In[12]:
import numpy as np
total_doc_num = 2472
doc_emb = np.zeros((total_doc_num, n_cluster))
doc_label = np.zeros((total_doc_num,), dtype=int)
import re
filename = "./data/Tweet"
doc_num = 0
with open(filename, 'r')as datafile:
sents = datafile.readlines()
punc = '",:'
for data in sents:
data = re.sub(r'[{}]+'.format(punc), '', data)
raw_text = data.split(' ')[1:-2]
doc_label[doc_num] = int(data.split(' ')[-1].strip().replace("}", ""))
for data_i in raw_text:
doc_emb[doc_num] += norm_topic_word_dis[:, word_id[data_i]]
doc_emb[doc_num] /= len(raw_text)
# doc_emb[doc_num]
doc_num += 1
datafile.close()
# In[19]:
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=89, max_iter=100).fit(doc_emb)
# In[14]:
from sklearn.metrics.cluster import normalized_mutual_info_score
# In[15]:
print("NMI_K_means=", normalized_mutual_info_score(np.array(doc_label), np.array(kmeans.labels_)))
print("ACC_K_means=", acc(np.array(doc_label), np.array(kmeans.labels_)))
# In[21]:
import warnings
warnings.filterwarnings('ignore')
avg_nmi = []
avg_acc = []
for i in range(20):
kmeans = KMeans(n_clusters=89, max_iter=100).fit(doc_emb)
avg_nmi.append(normalized_mutual_info_score(np.array(doc_label), np.array(kmeans.labels_)))
avg_acc.append(acc(np.array(doc_label), np.array(kmeans.labels_)))
print("avg_nmi: ", np.mean(avg_nmi))
print("avg_acc: ", np.mean(avg_acc))2.6 统计分析
为对聚类结果(avg_value等)进行统计分析,三次使用sys库,并将相关结果写入Tweet_gsdmm_emb.txt中,代码如下:
Y = [str(i) for i in list(doc_label)]
X = [str(i) for i in list(np.arange(total_doc_num))]
# In[14]:
import sys
if not sys.warnoptions:
import warnings
warnings.simplefilter("ignore")
avg_value = []
for i in np.arange(0.1, 1.0, 0.1):
# for i in np.arange(0.01, 0.11, 0.01):
clf_ratio = np.round(i, 2)
clf = Classifier(vectors=doc_emb, clf=LogisticRegression())
avg_value.append(clf.split_train_evaluate(X, Y, clf_ratio)['micro'])
print(clf_ratio, " ", clf.split_train_evaluate(X, Y, clf_ratio)['micro'])
print(np.mean(avg_value))
# In[15]:
import sys
if not sys.warnoptions:
import warnings
warnings.simplefilter("ignore")
avg_value = []
for i in np.arange(0.1, 1.0, 0.1):
# for i in np.arange(0.01, 0.11, 0.01):
clf_ratio = np.round(i, 2)
clf = Classifier(vectors=doc_emb, clf=LogisticRegression())
avg_value.append(clf.split_train_evaluate(X, Y, clf_ratio)['macro'])
print(clf_ratio, " ", clf.split_train_evaluate(X, Y, clf_ratio)['macro'])
print(np.mean(avg_value))
# In[16]:
import sys
if not sys.warnoptions:
import warnings
warnings.simplefilter("ignore")
avg_value = []
for i in np.arange(0.1, 1.0, 0.1):
# for i in np.arange(0.01, 0.11, 0.01):
clf_ratio = np.round(i, 2)
clf = Classifier(vectors=doc_emb, clf=LogisticRegression())
avg_value.append(clf.split_train_evaluate(X, Y, clf_ratio)['accuracy'])
print(clf_ratio, " ", clf.split_train_evaluate(X, Y, clf_ratio)['accuracy'])
print(np.mean(avg_value))
# In[17]:
storefile = 'Tweet_gsdmm_emb.txt'
sf = open(storefile, 'w')
for i in range(doc_emb.shape[0]):
sf.write(str(i) + " " + " ".join([str(ele) for ele in doc_emb[i]]) + '\n')
sf.close()3.代码测试
将项目导入到Pycharm后,修改Tweet数据集地址,运行Tweet_gsdmm.py,结果如下:
3.1 GSDMM
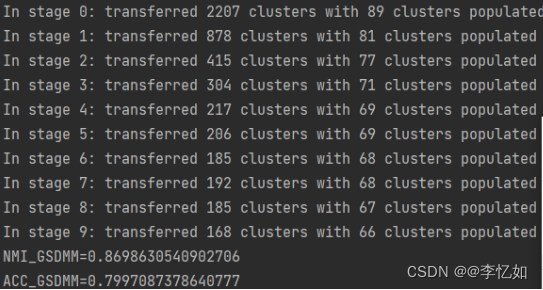
GSDMM的聚类过程与NMI及ACC测试结果如图9所示:
图9 GSDMM的聚类过程与测试结果
分析:由图9可见,GSDMM成功将Tweet数据集进行聚类,测试过程中NMI为0.8699,ACC为0.7997。
3.2 K-means
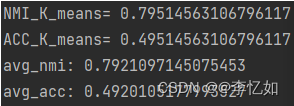
K-means的聚类及统计分析结果如图10所示:
图10 K-means的聚类及统计分析结果
分析:由图10可见,K-means成功将Tweet数据集进行聚类,测试过程中NMI为0.7951,ACC为0.4951。平均NMI为0.7921,平均ACC为0.4920,均低于GSDMM,验证了GSDMM的优越性。
3.3 相关数据展示
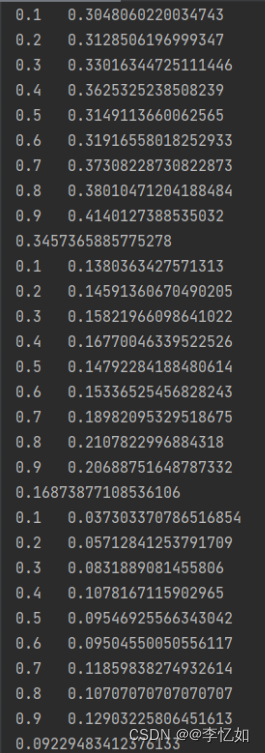
在GSDMM与K-means聚类均结束后,如代码解析所示,使用sys进行三次数据处理,clf_ratio与其对应的分词训练评估以及avg_value的平均值展示如图11所示,最后将其写入Tweet_gsdmm_emb.txt文件,文件部分展示如图12所示:
图11 相关数据展示
图12 Tweet_gsdmm_emb.txt部分文件展示
4.统计结果分析
为直观说明论文中GSDMM在短文本聚类中相较其他模型的优越性以及参数对聚类效果的影响,本部分将使用实验数据统计分析,并进行绘图可视化。
4.1 GSDMM的优越性
分别使用GSDMM、K-means、HAC、DMAFP四种聚类模型对Tweet数据集进行聚类,并统计其NMI与ACC,实验进行20次取平均值,数据汇总如表5所示,效果对比如图13所示:
表5 不同模型的聚类指标数据汇总
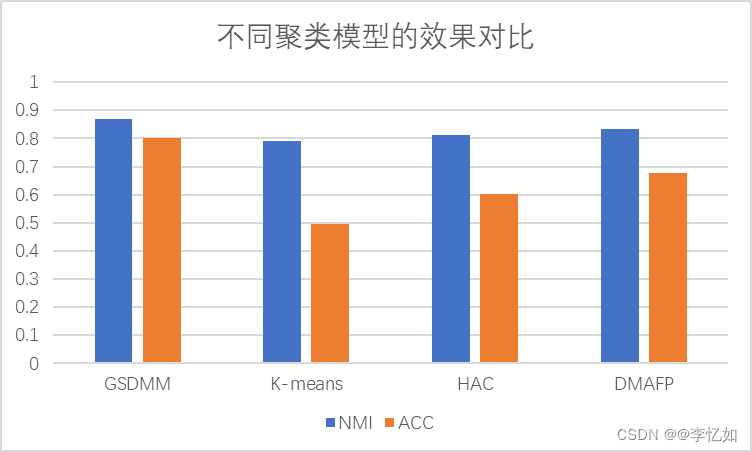
图13 不同聚类模型的效果对比
分析:由表5与图13可见,在以NMI与ACC为聚类指标的实验中,GSDMM的聚类效果均优于其他三种聚类模型,可验证其算法在短文本聚类的优越性。
4.2 参数对聚类效果的影响
为探究不同参数对GSDMM聚类效果的影响,改变参数,进行实验,记录数据并汇总分析。
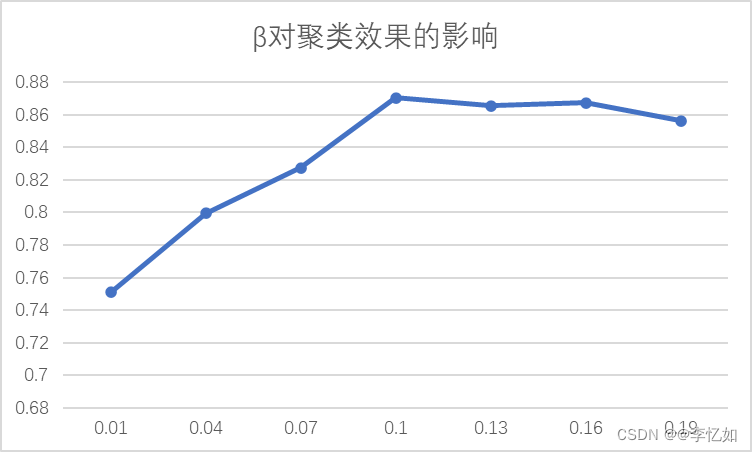
本实验以探究β对聚类效果的影响为例,确定K=8, alpha=0.1, n_iters=30,改变beta的值,观察NMI的变化。数据汇总如表6所示,影响趋势图如图14所示:
表6 β对聚类效果的影响数据汇总
图14 参数β对聚类效果的影响
分析:由图可见,不同β的取值对聚类效果有较大影响。随着β增大,NMI的值先快速上升再缓慢下降至稳定,在β为0.1左右聚类效果最好,与论文结论一致。
四、问题与补充
1.问题
1.1 问题描述
本实验进行过程中在项目导入过程中出现了问题,如图15所示:
图15 项目导入问题
经官网查阅,linear_assignment被弃用,官方将scipy.optimize.linear_sum_assignment代替了sklearn.utils.linear_assignment_,即使用from scipy.optimize import linear_sum_assignment as linear_assignment命令代替原导入即可,但随之出现图16问题:
图16 替换导入新问题
分析:在替换导入后部分同名函数实现方式有变,导致接收返回值的数量有变。
1.2 解决方案
故放弃更改导入,转用降低scikit-learn版本的方法去解决问题(官方在0.23版本弃用,下载低版本即可),可使用pip install -i https://pypi.douban.com/simple scikit-learn==版本命令,或在设置中指定版本。
降低版本后,测试运行成功,结果在上文有详述。
2.数据集介绍
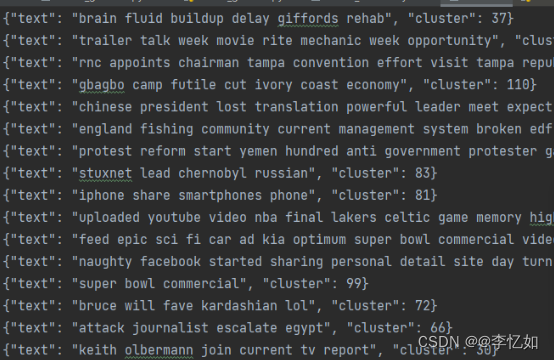
本实验主要使用数据集为Tweet数据集,包含2472条短文本数据,部分数据集展示如图17所示:
图17 Tweet数据集部分展示
3.GSDMM与LDA
本实验无论是MGP过程还是Tweet数据集(2472条数据)聚类均为短文本小数据集,要想探究GSDMM在长文本聚类或者大数据集聚类的情况,本部分将GSDMM与LDA进行比较。
参考实验:短文本主题模型:LDA与GSDMM - 知乎 (zhihu.com)
3.1 LDA简介
LDA为目前最流行的主题模型算法之一,其假设每个文档(在我们的例子中是tweet)包含多个主题,并计算每个主题对文档的贡献,且需要提前设置主题的数量。算法模型如图18所示:
图18 LDA算法模型
3.2 性能比较
为了比较这GSDMM与LDA两种主题模型方法的性能,我们可以选择关注3个关键参数:
Ⅰ、运行时间
在参考实验中,LDA在约1小时内可处理6m的数据集,而GSDMM只能处理300K左右,这意味着在运行时方面,LDA的性能远远优于GSDMM。不仅如此,就所有实际目的而言,我们可以说GSDMM无法处理超大数据集,至少不能一次性处理。另外,截至2022.11,GSDMM还不能并行化。
Ⅱ、建模主题的连贯性和一致性
在参考实验中,对于建模主题的连贯性和一致性,GSDMM比LDA做得更好。LDA输出在每个迭代中变化很大,总体上更混乱。
Ⅲ、主题连贯得分
原理补充:主题连贯性得分是一个客观的衡量标准,它植根于语言学的分布假设:具有相似意义的词往往出现在相似的语境中。如果所有或大部分单词密切相关,则主题被认为是连贯的。
在参考实验中,在主题连贯得分方面,GSDMM在其输出的主题的连贯性和一致性方面远远优于LDA。
3.3 结论
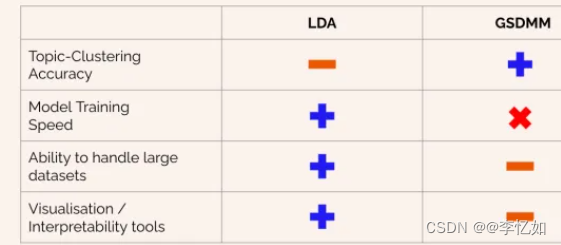
LDA与GSDMM的优缺点如图19所示:
图19 LDA与GSDMM的优缺点
分析:由②中的性能比较结果与图19进行分析,LDA与GSDMM的优劣取决于实验者的诉求与数据库的大小与类型。
LDA相对简单且高效,尤其是对于长文本与大数据集。GSDMM实现相对复杂与低效,但在任务完成程度(即建模主题的连贯性和一致性与主题连贯得分等部分)更加优秀,尤其是在短文本分类任务中。
4.模型补充
除了GSDMM模型,近年来还有很多新的模型(传统机器学习、深度学习)应用于短文本分类,如FastText、TextCNN、TextRNN、TextRNN + Attention、TextRCNN等,均取得了不错的效果。
五、参考资料
1.A Dirichlet Multinomial Mixture Model-based Approach for Short Text Clustering
2.GitHub - rwalk/gsdmm: GSDMM: Short text clustering
3.短文本主题模型:LDA与GSDMM - 知乎 (zhihu.com)
总结
(1)GSDMM有以下几个优点:
1.可以在完备性和一致性之间保持平衡;
2.可以很好的处理稀疏、高纬度的短文本;
3.较其它的聚类算法,在性能上表现更为突出。
(2)不同参数对GSDMM的聚类效果有不同影响,对于不同的数据集(各个数据集差异较大)最佳的参数取值也会不同。在实际应用中,当给定较好的经验参数,GSDMM具备较好的聚类效果,这使得它具备较高的应用价值。
(3)相较LDA等常用文本分类模型,GSDMM实现相对复杂与低效,但在任务完成程度(即建模主题的连贯性和一致性与主题连贯得分等部分)更加优秀,尤其是在短文本分类任务中。
(4)针对不同数据集与不同需求,应使用不同聚类模型。