文章目录
一、树
1.定义部分
一个N个结点的树有N-1条边
树是保证结点连通的最小的一种连接方式
2.基本术语
(1)结点的度(Degree):结点的子树个数
(2)树的度:树的所有结点中最大的度数
(3)叶结点(Leaf)、子结点(Parent)、父结点(Parent)、子结点(Child)、兄弟结点(Sibling)
(4)路径和路径长度:结点序列,前一个是后一个的父结点。路径所包含的边的个数为路径的长度
(5)祖先结点(Ancestor),子孙节点(Descendant)
(6)结点的层次(Lever):
规定
\color{red}{规定}
规定根结点在1层,其它任一结点的层数是其父结点的层数加1
(7)树的深度(Depth):树的所有结点中的最大层次是这棵树的深度
3.树的表示
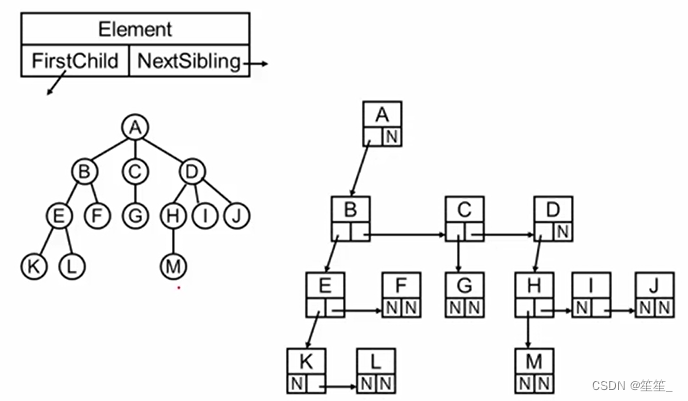
(1)儿子-兄弟表示法
“长兄为父,带下一个兄弟”
(2)森林的表示:将每个根结点作为兄弟结点串联起来
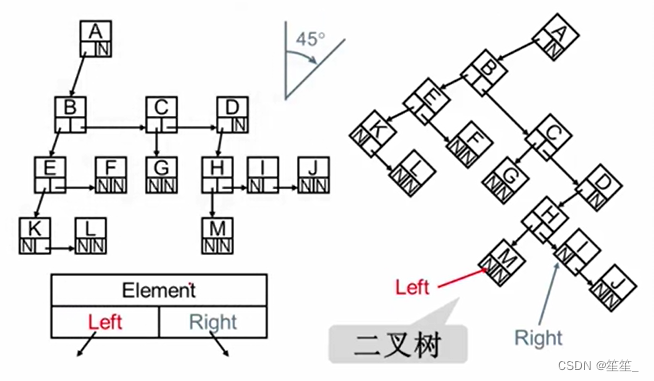
向右旋转45度
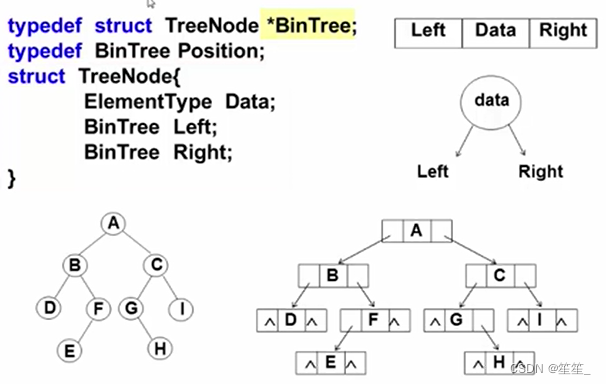
4.二叉树的链表结构
typedef struct TNode *Position;
typedef Position Bintree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
二、二叉树
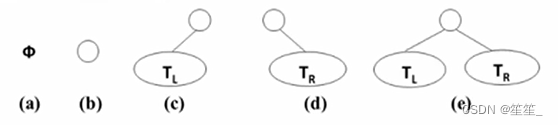
1.定义
二叉树具有五种基本形态
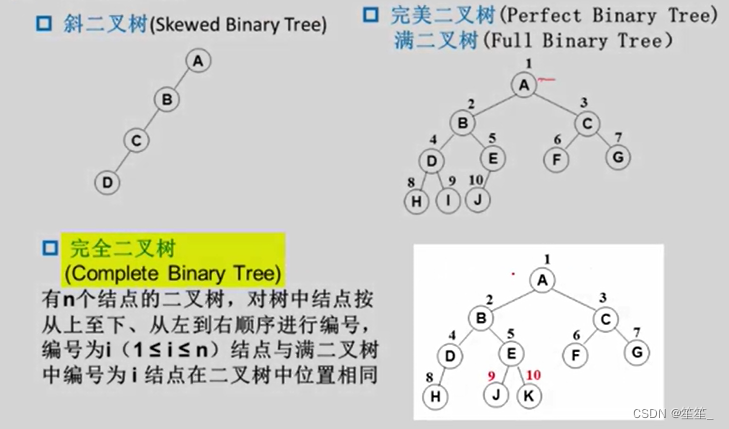
2.特殊二叉树
3.二叉树的几个重要性质
(1)一个二叉树第i层的最大结点数为:2i-1,i >=1
(2)深度为k的二叉树有最大结点总数为:2k-1,k >=1(完美二叉树)
(3)对于非空二叉树T,若n0表示叶结点的个数、n2表示度为2的非叶结点个数,那么两者满足关系n0=n2+1
4.二叉树的抽象数据类型定义
5.二叉树的存储结构
(1)顺序存储结构
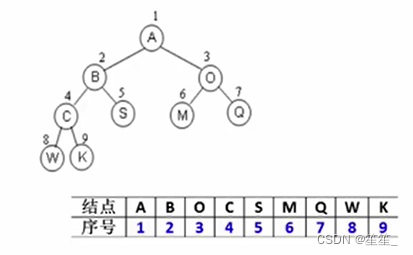
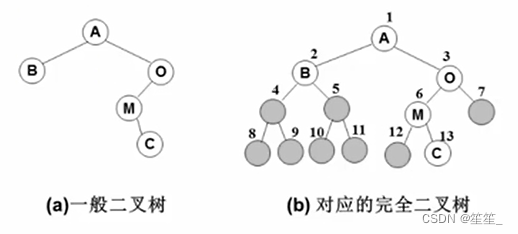
完全二叉树:按从上到下、从左到右顺序存储n个结点
非根结点(序号 i>1)的父结点的序号是 [ i / 2 ]
结点(序号为i)的左孩子结点的序号是2i
结点(序号为i)的右孩子结点的序号是2i+1
一般二叉树也可以采用这种结构,但会造成空间浪费…
(2)链表存储
三、关于二叉树的基本操作
1.二叉树的递归遍历
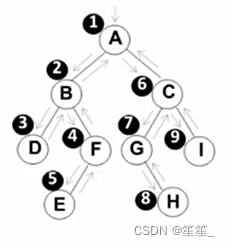
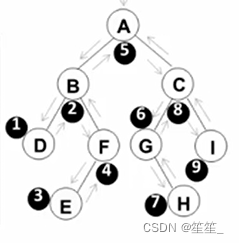
(1)先序遍历
遍历顺序:A BDFE CGHI
//先序遍历
void PreOrderTraversal(BinTree BT)
{
if(BT){
printf("%d",BT->Data);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
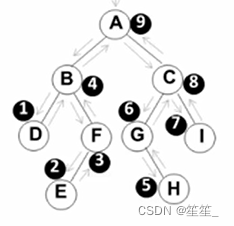
(2)中序遍历
遍历顺序:DBEF A GHCI
//中序遍历
void InOrderTraversal(BinTree BT)
{
if(BT){
PreOrderTraversal(BT->Left);
printf("%d",BT->Data);
PreOrderTraversal(BT->Right);
}
}
(3)后序遍历
遍历顺序:DEFB HGIC A
//后序遍历
void PostOrderTraversal(BinTree BT)
{
if(BT){
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
printf("%d",BT->Data);
}
}
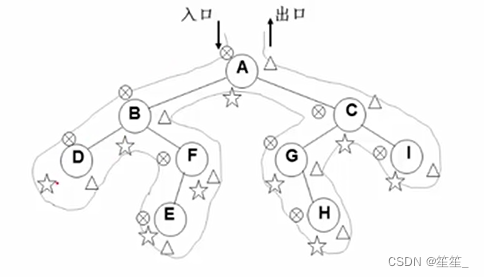
先序、中序、后序便利的过程:遍历过程中经过结点的路线一样,只是访问各结点的时机不同
图中三种符号分别标记出先序、中序、后序访问各节点的时刻
2.二叉树的非递归遍历(中序)
实现的基本思路:使用堆栈
算法思路:
遇到一个结点,将它压站后遍历其左子树。
左子树遍历结束后从栈顶弹出这个元素并访问它
然后按其右指针再去中序遍历该结点的右子树。
void InOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = CreateStack(MaxSize);
while(T || !IsEmpty(S)) {
while(T){
Push(S,T);
T = T->Left;
}
if(!IsEmpty(S)){
T = Pop(S);
printf("%5d",T->Data);
T = T->Right;
}
}
}
先序遍历即在第一次遇到这个元素时就将它输出,于是将printf语句放在第一次push后面即可。
3.二叉树的层序遍历
二叉树遍历的核心问题:二维结构的线性化
- 需要一个存储结构保存暂时不访问的结点
- 存储结构:堆栈(保存自己)、队列(保存右儿子)
队列实现思路:
从根节点开始,首先将根结点入队
然后开始执行循环: 结点出队、访问该节点、其左右儿子入队
//层序遍历
void LevelOrderTraversal(BinTree BT)
{
Queue Q;
BinTree T;
if(!BT) return; //如果是空树直接返回
Q = createQueue(MaxSize);
Add(Q,BT);
while(!IsEmptyQ(Q)){
T = DeleteQ(Q);
printf("%d\n",T->Data);
if(T->Left) AddQ(Q,T->Left);
if(T->Right) AddQ(Q,T->Right);
}
}
四、遍历二叉树的应用
1.输出二叉树的叶子结点
在二叉树遍历算法中增加检测结点的左右子树是否都为空
void PreOrderPrintLeaves(BinTree BT)
{
if(BT){
if(!BT->Left && !BT->Right)
printf("%d",BT->Data);
PreOrderPrintLeaves(BT->Left);
PreOrderPrintLeaves(BT->Right);
}
}
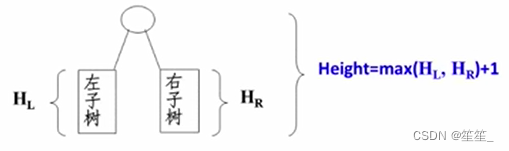
2.求二叉树的高度
需要知道左右子树的高度才可知整个树的高度,因此是后序遍历
int PostOrderGetHeight(BinTree BT)
{
int HL.HR,MAXH;
if(BT){
HL = PostOrderGetHeight(BT->Left);
HR = PostOrderGetHeight(BT->Right);
MaxH = (HL > HR) ? HL:HR;
return (MaxH + 1);
}
else return 0; //空树深度为0
}
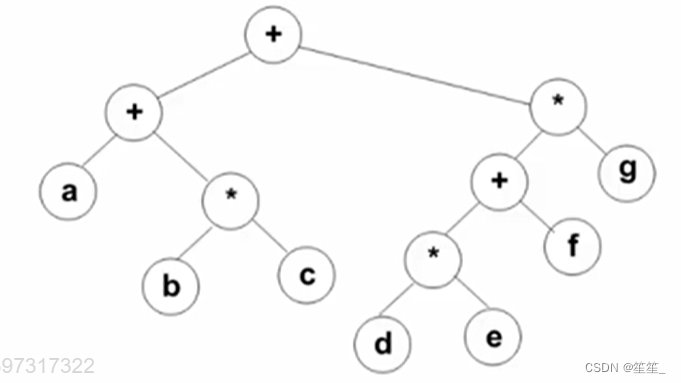
3.二元运算表达式树及其遍历
三种遍历得到三种不同访问结果:
注意:中缀表达式会受到运算符优先级的影响
4.由两种遍历序列确定二叉树
必须要有中序遍历才能确定一个二叉树
前序和后序无法判断左右的边界