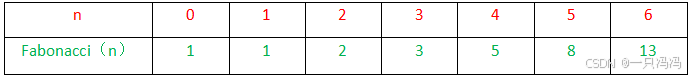折半查找

思路：

• 要查找的key值等于位于数组中央mid处的值，直接返回mid
• key值比中间的值大，向右继续寻找
• key值比中间的值小，向左继续寻找

递归实现

int Binary_Search1(int data[],int key,int low,int high){
	int mid = (low+high)/2;
	if(low>high){
		return -1;
	}
	if(key == data[mid]){
		return mid;
	}else if(key > data[mid]){//key值比中间的值大，向右继续寻找 
		return Binary_Search1(data,key,mid+1,high);
	}else{
		return Binary_Search1(data,key,low,mid-1);
	} 
}

非递归实现

int  Binary_Search2(int data[],int key,int low,int high){
	int mid;
	while(low<=high){
		mid = (low+high)/2;
		if(data[mid] == key){
			return mid;
		}else if(data[mid] > key){
			high = mid-1;
		}else{
			low = mid+1;
		}
	}
}

斐波那契数列/兔子问题

斐波那契数列（Fibonacci Sequence）是数学中一个经典的数列，其特点是每一项都是前两项之和。最初，这个数列是在研究兔子繁殖问题时被提出的，但后来被发现有广泛的数学和自然界应用。
数列的定义为：
第0项：( F(0) = 1 )
第1项：( F(1) = 1 )
从第2项开始： ( F ( n ) = F ( n − 1 ) + F ( n − 2 ) ) （ ( n ≥ 2 ) ）

功利性解题技巧：

• 根据函数，在草稿纸上写出对应自变量x与因变量y的表格，观察表格中相邻数据之间的关系
  

递归实现

 int Fibo1(int n){
 	if(n <= 1){
 		return 1;
	 }
	 return Fibo1(n-1)+Fibo1(n-2);
 }  

非递归实现

int Fibo2(int n){
	if(n <= 1){
		return 1;
	}
	int f0 = 1,f1 = 1;
	int c;
	for(int i = 2;i <= n;i++){
		c = f0 + f1;
		f0 = f1;
		f1 = c;
	}
	return c;
}