1.数据结构的定义
数据是描述客观事物的数、字符以及所有能输入到计算机中并被计算机程序处理的符号的集合。
数据元素是数据的基本单位(例如,A公司中的每个员工记录都是一个数据元素),即数据元素是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理。
数据项是具有独立含义的数据最小单位,也称为成员或域(例如,A公司中每个数据元素即员工记录是由工号、姓名、年龄、性别和部门等数据项组成)。一个数据元素可以由若干个数据项组成。
数据对象是性质相同的有限个数据元素的集合,它是数据的一个子集,如大写字母数据对象是集合C={'A','B','C',…,'Z'};1~100的整数数据对象是集合N={1,2,…,100}。 默认情况下,数据结构中的数据指的是数据对象。
数据结构是指所涉及的数据元素的集合以及数据元素之间的关系,由数据元素之间的关系构成结构,因此可以把数据结构看成带结构的数据元素的集合。数据结构包括以下几个方面。
| 数据逻辑结构 | 由数据元素之间的逻辑关系构成,是数据结构在用户面前呈现的形式。 |
| 数据存储结构 | 指数据元素及其关系在计算机存储器中的存储方式,也称为数据的物理结构。 |
| 数据运算 | 指施加在数据上的操作。 |
数据的逻辑结构是从逻辑关系(主要是数据元素的相邻关系)上描述数据的,它与数据的存储无关,是独立于计算机的,因此数据的逻辑结构可以看作从具体问题抽象出来的数据模型。
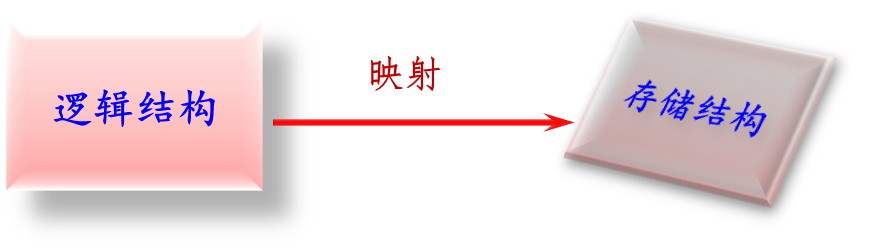
数据的存储结构是逻辑结构用计算机语言的实现或在计算机中的表示(也称为映像),也就是逻辑结构在计算机中的存储方式,它是依赖于计算机语言的。一般在高级语言(例如Python、Java、和C/C++等语言)的层次上讨论存储结构。
数据的运算是定义在数据的逻辑结构之上的,每种逻辑结构都有一组相应的运算,最常用的运算有检索、插入、删除、更新、排序等。数据的运算最终需要在对应的存储结构上用算法实现。
2.数据的逻辑结构
数据的逻辑结构是面向用户的,它反映数据元素之间的逻辑关系而不是物理关系。数据的逻辑结构是独立于计算机的。
2.1逻辑结构的表示
由于数据逻辑结构是面向用户的,可以采用表格、图等用户容易理解的形式表示。
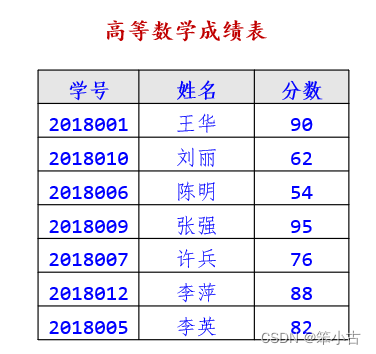
如:
为了更通用地描述数据的逻辑结构,通常采用二元组表示数据的逻辑结构,一个二元组如下:
B=(D,R)
其中,B是一种逻辑数据结构,D是数据元素的集合,在D上数据元素之间可能存在多种关系,R是所有关系的集合。即:
D={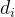
R={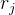
R中的某个关系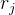
若某个元素没有前驱元素,则称该元素为开始元素;若某个元素没有后继元素,则称该元素为终端元素。
对于对称序偶,即满足这样的条件:若<x,y>∈r(r∈R),则<y,x>∈r(x,y∈D),可用圆括号代替尖括号,即(x,y)∈r。
.对于D中的每个数据元素,通常用一个关键字来唯一标识,例如高等数学成绩表中学生成绩记录的关键字为学号。
2.2逻辑结构的类型
数据的逻辑结构与数据元素本身的内容无关,也与数据元素的个数无关。数据的逻辑结构主要分为以下类型。
集合:结构中数据元素之间除了“同属于一个集合”的关系外,没有其他关系,与数学中的集合概念相同。
线性结构:若结构是非空的,则有且仅有一个开始元素和终端元素,并且所有元素最多只有一个前驱元素和一个后继元素。
树形结构:若结构是非空的,则有且仅有一个元素为开始元素(也称为根结点),可以有多个终端元素,每个元素有零个或多个后继元素,除开始元素外每个元素有且仅有一个前驱元素。
图形结构:若结构是非空的,则每个元素可以有多个前驱元素和多个后继元素。
3.数据的存储结构
数据在计算机存储器中的存储方式就是存储结构。它是面向程序员的。
存储实现的基本目标是建立数据的机内表示,包括数据元素的存储和数据元素之间关系的存储两个部分。逻辑结构是存储结构的本质,设计数据的存储结构称为从逻辑结构到存储器的映射。
有常用的4种存储结构类型:
顺序存储结构:
所有元素存放在一片地址连续的存储单元中。
逻辑上相邻的元素在物理位置上也是相邻的,所以不需要额外空间表示元素之间的逻辑关
系。
优点:节省存储空间;缺点:初始空间大小难以确定,插入和删除操作需要移动较多的元素。
链式存储结构:
数据元素存放在任意的存储单元中,这组存储单元可以是连续的,也可以是不连续的。
通过指针域来反映数据元素的逻辑关系。
优点:便于进行插入和删除操作,实现这些操作仅需要修改相应结点的指针属性,不必移动结点;缺点:存储空间的利用率较低。
索引存储结构:
在存储元素信息的同时建立附加的索引表,索引表中的每一项称为索引项,索引项的一般形式为(关键字,地址),关键字唯一标识一个元素,索引表按关键字有序排列,地址作为指向元素的指针。
优点:可以对元素进行随机访问,在进行插入、删除运算时,只需要移动存储在索引表中对应元素的存储地址,而不必移动存放在元素表中元素的数据;缺点:增加了索引表,降低了存储空间的利用率。
哈希存储结构:
根据元素的关键字通过哈希(或散列)函数直接计算出一个值,并将这个值作为该元素的存储地址。
优点:查找速度快,只要给出待查元素的关键字,就可以立即计算出该元素的存储地址;缺点:一般只适用于要求对数据进行快速查找和插入的场合。
与前3种存储结构不同的是,哈希存储结构只存储元素的数据,不存储元素之间的逻辑关系。
4.数据的运算
将数据存放在计算机中的目的是为了实现一种或多种运算。运算包括功能描述(或运算功能)和功能实现(或运算实现)。前者是基于逻辑结构的,是用户定义的,是抽象的。后者是基于存储结构的,是程序员用计算机语言或伪码表示的,是详细的过程,其核心是设计实现某一运算功能的处理步骤,即算法设计。
对于一种数据结构,其逻辑结构是唯一的,但它可以对应多种存储结构。
同样的运算,在不同的存储结构中,其实现过程是不同的。
5.数据结构和数据类型
5.1数据类型
数据类型是程序设计中最重要的基本概念之一。在程序中描述的、通过计算机处理的数据通常属于不同的类型,例如整数、浮点数等。每个类型包含一组合法的数据对象,并规定了对这些对象的合法操作。
在Python中,基本数据类型包括布尔类型(bool)、数值类型(int和float)、字符串类型(str)和一些组合数据类型。
数据结构是指计算机处理的数据元素的组织形式和相互关系,而数据类型是某种程序设计语言中已实现的数据结构。
5.2抽象数据类型
抽象数据类型指的是用户进行软件系统设计时从问题的数据模型中抽象出来的逻辑数据结构和逻辑数据结构上的运算,而不考虑计算机的具体存储结构和运算的具体实现算法。
抽象数据类型有两个重要特征:数据抽象和数据封装。数据抽象是指用ADT描述程序处理的实体时强调的是其本质的特征、其所能完成的功能以及它和外部用户的接口。数据封装是指将实体的外部特性和其内部实现细节分离,并且对外部用户隐藏其内部实现细节。数据抽象类型需要通过固有数据类型(高级编程语言中以实现的数据类型,例如Python中的类)来实现。