一、旅行商问题简介
旅行商问题
TSP,即旅行商问题,又称TSP问题(Traveling Salesman
Problem),是数学领域中著名问题之一。
问题概述
假设有一个旅行商人要拜访N个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个NPC问题。
问题由来
TSP的历史很久,最早的描述是1759年欧拉研究的骑士周游问题,即对于国际象棋棋盘中的64个方格,走访64个方格一次且仅一次,并且最终返回到起始点。
TSP由美国RAND公司于1948年引入,该公司的声誉以及线形规划这一新方法的出现使得TSP成为一个知名且流行的问题。
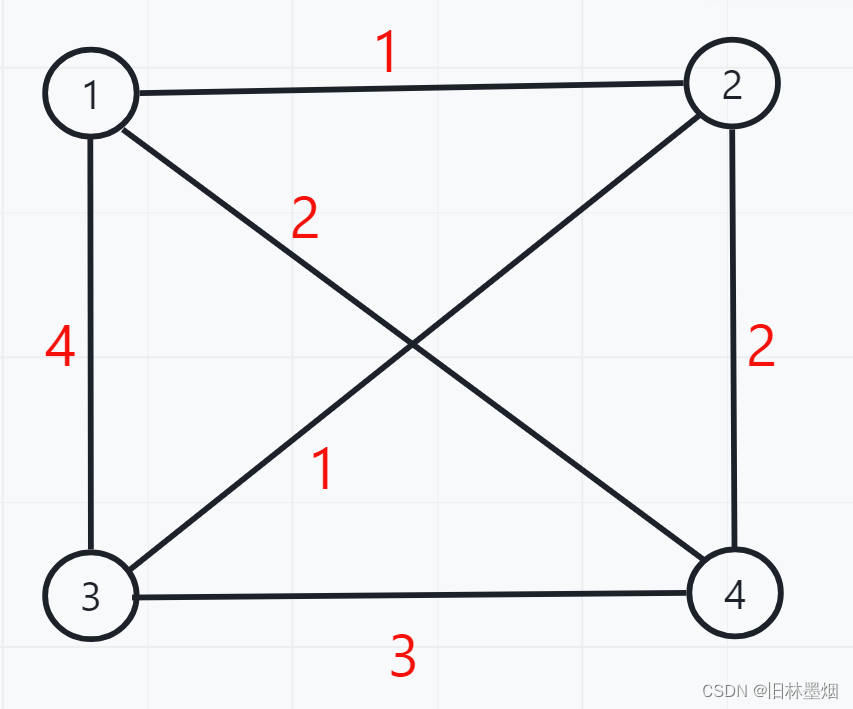
示例:
黑色数字代表点、红色代表路径的花费
输入:
4 6
1 2 1
1 4 2
1 3 4
2 3 1
2 4 2
3 4 3
输出:
运行中...
最短距离为:7
共2条最短路径:
路径1:1-->4-->3-->2-->1
路径2:1-->2-->3-->4-->1
提示:
第一行输入点的个数n和边的个数m,点的编号为1~n
接下来m行输入m条边以及花费,p1 p2 v,表示点p1和点p2之间有一条无向边,边的花费为v
二、基本思路
1、我们需要知道,我们求的路径是一个环,所以无论从哪里开始,结果都应该是一样的,就像例题中的;
最短路径可表示为 1–>4–>3–>2–>1
那么它也可以表示为 4–>3–>2–>1–>4
还可以表示为 3–>2–>1–>4–>3
所以我们可以从任意的点出发去查找路径
2、旅行商问题只有当图是哈密顿图时才可能有解的,即需要满足题意,可以从一个点出发,到达所有的点一次,然后回到起点。
这个可以通过最后运行的结果判断,我们令初始答案是一个很大的值,如果查找后答案没有被改变,则该图无解
3、按照传统的暴力搜索,时间复杂度为O(n!),而动态规划可以将复杂度减低到O(n2*2n)
4、有个注意的点,起点需要走两遍,为了简化问题,只需要预处理从起点走到其它点的最小花费,而起点不能标记为已经走过,因为后面还有回到原点
三、实现
1、状态压缩
我们需要表达我们已经走过了哪些点,目前到达了哪里,有什么办法表达出来呢?
暴力是万能的,我们可以开一个数组dp[i][j],代表目前到达了i点,dp[i][j]的值代表j点是否已经走过了,但是这样做的话我们状态转移会变得很麻烦,状态压缩就是它的优化
状态压缩是通过二进制实现的,我们知道int有32位,那么我们可以用第0位代表第0个点的状态,第1位代表第1个点状态…第n位代表第n个点的状态,位的值如果是1的话就代表该点已经走过了,例如17的二进制为0000010001,代表第0个点和第4个点已经走过了
那么我们可以开一个数组dp[i][j],代表目前走到了i点,用j代表已经走过了哪些点,例如:
dp[0][17],17的二进制为0000010001,代表目前在第0个点,已经走过第0个点和第4个点。
dp[4][17],17的二进制为0000010001,代表目前在第4个点,已经走过第0个点和第4个点。
我们可以用dp[i][j]的值代表当前这个状态的最小花费,例如dp[0][17]=12,那么就代表到达该状态需要的最小花费是12
2、状态转移
dp的基本思想就是记录某个状态的最优解,再从目前的状态转移到新的状态,从局部最优解转移到全局最优解
我们用数组a[i][j]存储图,那么a[i][j]的值就代表从i点到j点的花费
我们如何求状态dp[0][19]的最优解?
19的二进制是0000010011,因为18的二进制为0000010010,那么dp[0][19]可以由dp[4][18],dp[1][18]转移过来,最小花费是dp[0][19]=min(dp[4][18]+a[4][0],dp[1][18]+a[1][0])
即我们要求大的状态,那么就需要先把小状态最优解求出来。反过来我们求出了所有小状态,那么就可以求出大状态的最优解
{1,2,3}代表第1、2、3个点都已经走过了
可以发现,小状态总是比大状态小的,那么我们可以从0状态枚举到2n-1状态,获取到每个状态的最优解
我们还可以反过来想,从小状态去更新大的状态
两种思路都可以
四、代码
下面代码是基于逆向思想的,即从小状态更新大状态。理解透了的同学不妨尝试写一下大状态调用小状态更新的代码
#include<bits/stdc++.h>
using namespace std;
int n,m;//n点的个数,m边的个数
int a[15][15];//邻接矩阵存无向图
int dp[15][1<<15];//dp[i][j]代表从最后走到i点到达状态j
int t;//一共有t个状态
void init(){//初始化
memset(a,0x3f,sizeof a);
memset(dp,0x3f,sizeof dp);
cout<<"请输入点和边的个数:"<<endl;
cin>>n>>m;
cout<<"请输入"<<m<<"条边:"<<endl;
for(int i=0;i<m;i++){
int x,y,val;
cin>>x>>y>>val;
x--;
y--;
a[x][y]=val;
a[y][x]=val;
}
}
void run(){//dp核心算法
t=(1<<n);
for(int i=1;i<n;i++){//因为起点初始不能被标记已经走过,所以需要手动初始化起点到达其它点的花费
dp[i][1<<i]=a[0][i];
}
for(int i=0;i<t;i++){//枚举每一个状态
for(int j=0;j<n;j++){//枚举每一个没有走过的点
if(((i>>j)&1)==0){
for(int k=0;k<n;k++){//枚举每一个走过的点
if(((i>>k)&1)==1&&dp[j][i^(1<<j)]>dp[k][i]+a[k][j]){//取最优状态
dp[j][i^(1<<j)]=dp[k][i]+a[k][j];
}
}
}
}
}
}
int tt;//记录
vector<int> path(1,0);//初始化从0点出发 ,存储单条路径
vector<vector<int> > paths;//存储所有的路径
void getPath(int p){//递归查找所有路径
if((tt^(1<<p))==0){//如果是最后一个点了就存储改路径
paths.push_back(path);
return;
}
for(int j=1;j<n;j++){
//回溯算法,一个加法的原则
//如果点1到达点5的最短距离为100,点1到达点3的最短距离是70
//而点3和点5之间的距离为30 ,那么点3是点1到5之间的一个中间点
//即1-->...-->3-->5
if(a[j][p]+dp[j][tt^(1<<p)]==dp[p][tt]){
tt^=(1<<p);
path.push_back(j);
getPath(j);
tt^=(1<<p);
path.pop_back();
}
}
}
void print(){//打印路径
cout<<"最短距离为:"<<dp[0][t-1]<<endl;
cout<<"共"<<paths.size()<<"条最短路径:" <<endl;
for(int i=0;i<paths.size();i++){
cout<<"路径"<<i+1<<":1";
for(int j=paths[i].size()-1;j>=0;j--){
cout<<"-->"<<paths[i][j]+1;
}
cout<<endl;
}
}
int main(){
init();
cout<<"运行中..."<<endl<<endl;
run();
cout<<"运行结果:"<<endl;
if(dp[0][t-1]==0x3f3f3f3f){//无解
cout<<"该图不是哈密顿图!"<<endl;
return 0;
}
tt=t-1;
getPath(0);
print();
}
五、复杂度分析
时间复杂度: 求最小花费枚举2n种状态,每种状态枚举每一个没有走过的点,每一个没走过的点需要枚举每一个已经走过的点,时间复杂度O(n2*2n),求所有路径,时间复杂度将退化为O(n!)
空间复杂度: 记录每个点的2n种状态,空间复杂度O(n*2n)