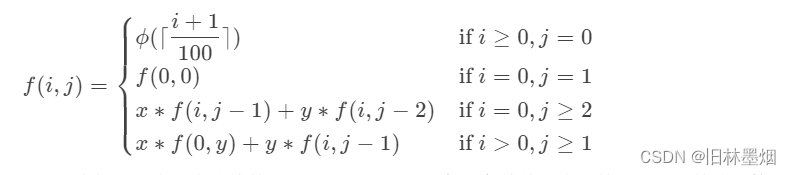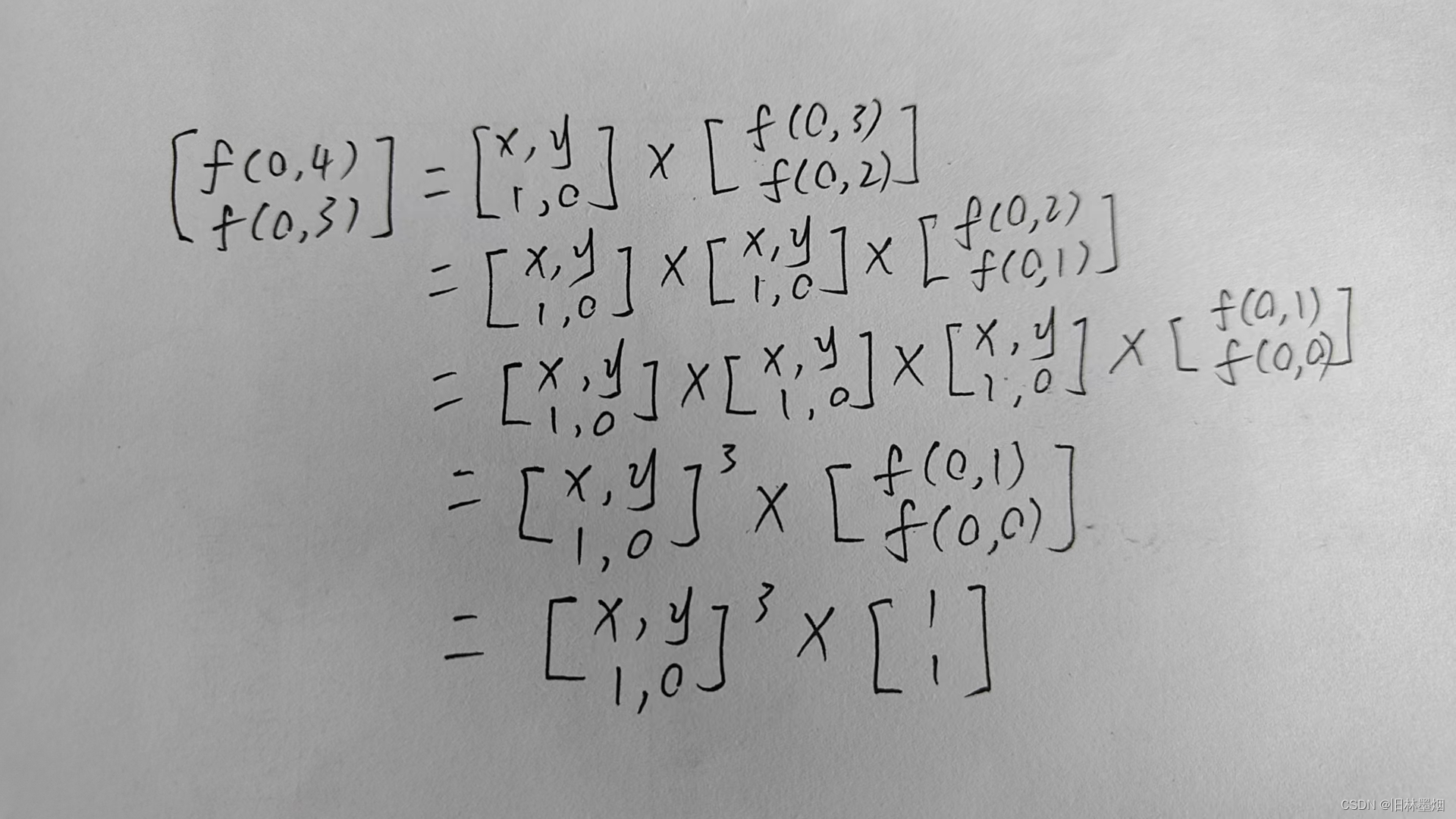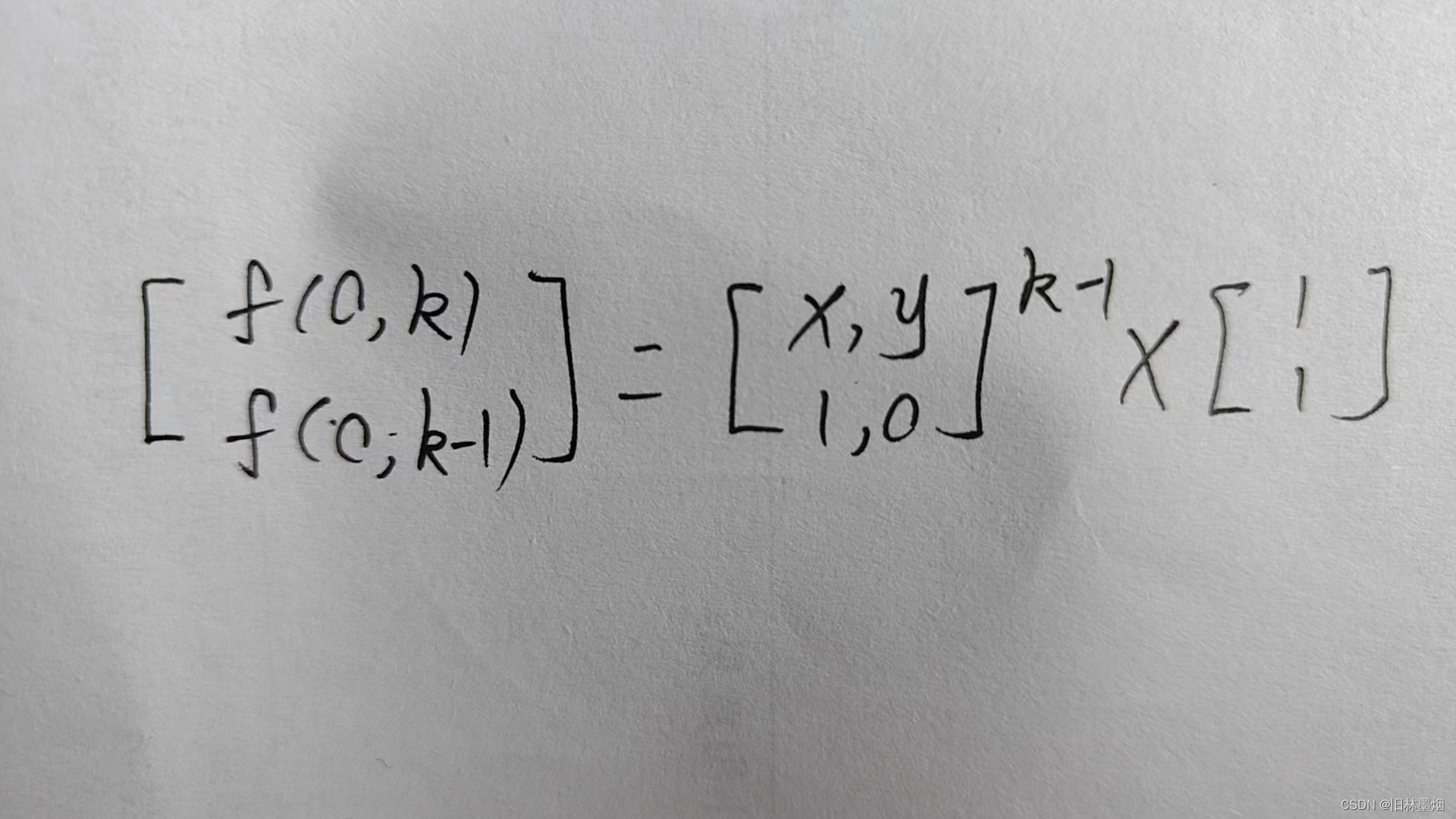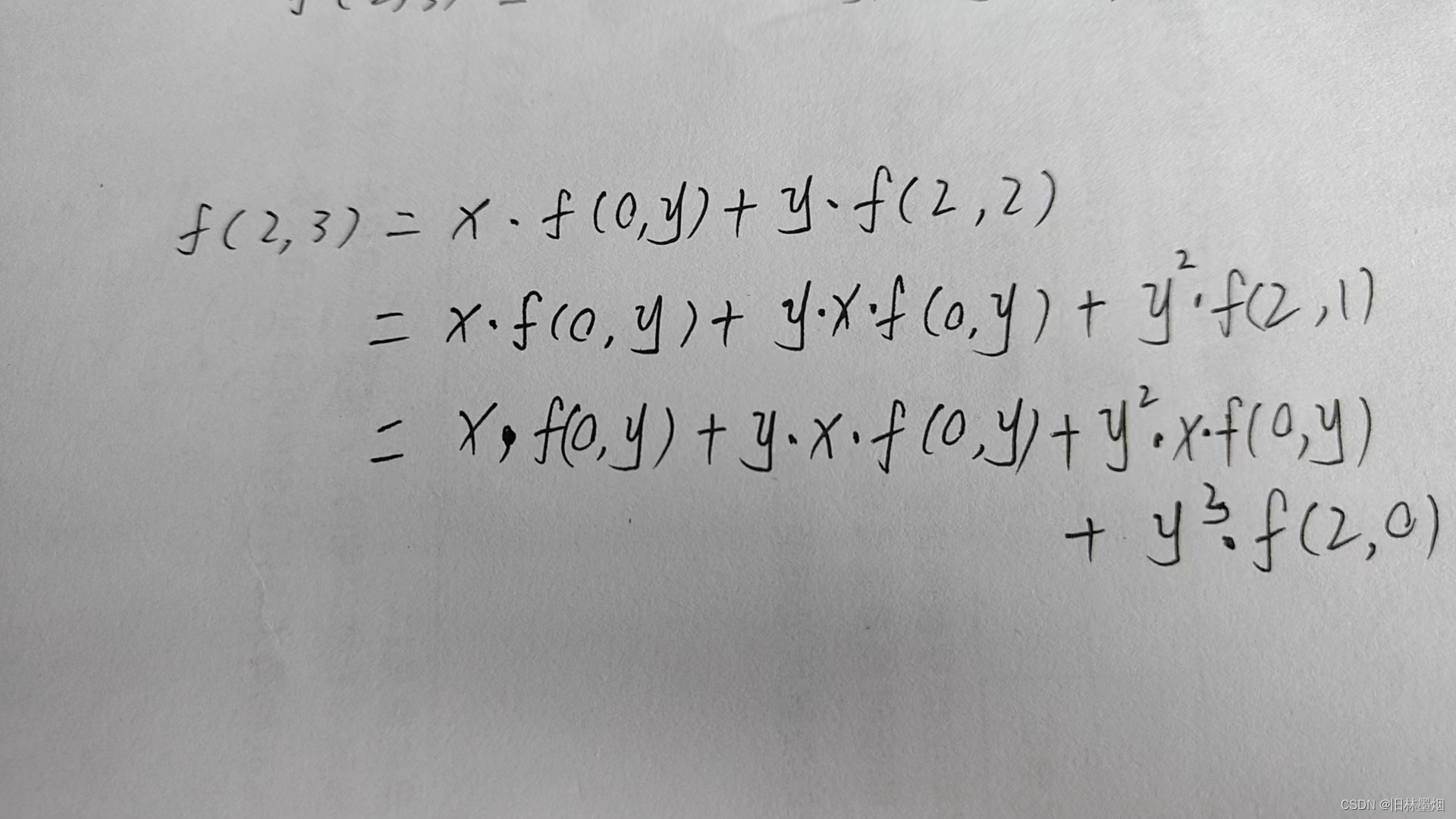惠州学院第二届大学生程序设计竞赛c++题解
题目总览
按难度等级排序
| 题目 | 难度 | 知识点 |
|---|---|---|
| 7-1 关于闭区间的最值问题 | 签到 | 二分答案 / 数学 |
| 7-4 Nomi的计算器 | 简单 | 栈+模拟 |
| 7-9 玛恩纳 | 简单 | 模拟 |
| 7-10 涂矩阵 | 简单 | 前缀和+差分 |
| 7-7 求和游戏 | 中等 | 贪心 |
| 7-2 大厂必备技能!!! | 中等 | 最短路径 |
| 7-8 得分王 | 中等 | 深搜+广搜 / 全排列+拓扑 |
| 7-5 篮球二叉树 | 稍难 | 思维+构造 |
| 7-3 这可能是道签到题 | 稍难 | 欧拉函数+矩阵+快速幂+等比数列 |
| 7-6 回文文回 | 难 | 线段树+字符串哈希 |
7-1 关于闭区间的最值问题
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
给定 T 组测试样例
每组样例给定整数 n,x,请输出区间 [1, n] 中能被 x 整除的最大整数。
【输入格式】
第一行输入一个整数T,代表一共有T组测试样例。(1 ≤ T ≤ 1000)
接下来 T 行,每行两个整数 n, x。(1 ≤ x ≤ n ≤ 109 )
【输出格式】
对每一组输入,在一行中输出答案值。
【样例输入】
5
10 6
6 6
4 2
9 1
7 5
【样例输出】
6
6
4
9
5
【方法一:二分搜索】
一种直观的方法,可以通过二分枚举倍率的方法找到符合条件的最大倍率,x乘于最大倍率就是答案,例如一组输入:
13 2
倍率可以选1、2、3、4、5、6、7、8、9、10
第一次选5,2*5=10,满足条件,那么缩短左边界
倍率可以选5、6、7、8、9、10
第二次选7,2*7=14,不满足条件,那么缩短右边界
倍率可以选5、6
第三次选6,2*6=12,满足条件,那么缩短左边界
倍率可以选6
最后确定最大的倍率是6,那么答案是6*2=12
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
int main(){ //主函数
int t;
cin>>t;
while(t--){
long long n,x;
cin>>n>>x;
long long l=1,r=1e9; //左边界l,右边界r
while(l<r){
long long mi=(l+r)/2+1; //取中位数mi
if(mi*x<=n){ //满足条件,左边界缩小
l=mi;
}else{ //不满足条件,右边界缩小
r=mi-1;
}
}
cout<<l*x<<endl; //打印答案
}
}
【方法二:数学】
简单的数学推论,n/x向下取整后再乘于x就是答案,例如一组输入:
13 2
答案是13/2*2=12
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
int main(){ //主函数
int t;
cin>>t;
while(t--){
long long n,x;
cin>>n>>x;
cout<<n/x*x<<endl;
}
}
7-2 大厂必备技能!!!
时间限制: 2.0s 内存限制:256.0MB
【问题描述】
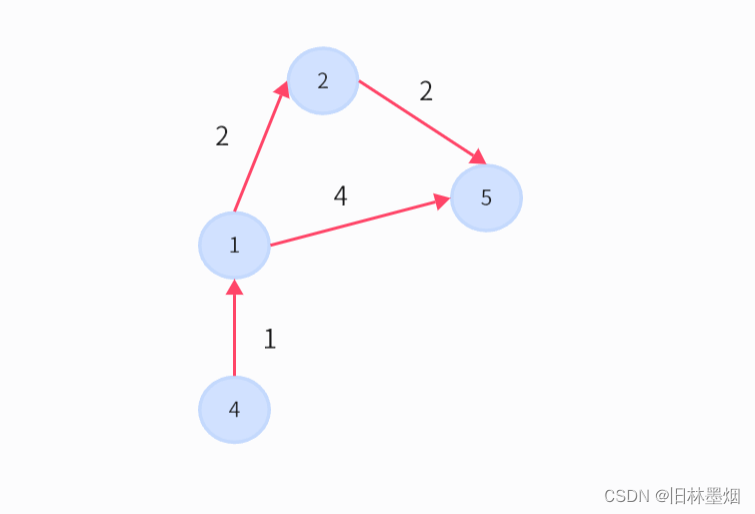
某团员工的素质不一般,天刚朦朦亮就准备让 iKun 和 Dij 去送快餐了。聪明的他们将自己居住的城市绘成一张地图,已知地图上有 n 个编号不同的城市,他们目前处在编号为 1 的城市上,送餐的目的地是编号为 n 的城市。此外,这些路都是单向的,从城市 u 到 v 需要花费 c 的时间。为了更高效地将快餐送到顾客手中,他们决定走从城市 1 到城市 n 花费最少的路。他们担心堵车,所以不能只知道一条路线,于是邀请你顺便探讨一下最少花费的路径有多少条?
【输入格式】
输入第一行为两个空格隔开的数 n (1 ≤ n ≤ 2000), m (0 ≤ m ≤ n∗(n−1)), 表示这张地图里有多少个城市及有多少边的信息。
下面 m 行,每行三个数 u, v, c, 表示从 u 城市到 v 城市有道路相连且花费为 c (1≤ c ≤10)。(其中保证 u
≠v,1 ≤ u,v ≤n,样例可能存在重边)
【输出格式】
输出包括两个数,分别是最少花费和花费最少的路径的总数。保证花费最少的路径总数不超过 2 30 。
两个不同的最短路径方案要求:长度均为最短路且每条路径经过的点的编号序列不同。
若无法到达城市 n,则在一行中输出 “No answer”。
【样例输入1】
5 4
1 5 4
1 2 2
2 5 2
4 1 1
【样例输出1】
4 2
【样例输入2】
5 2
1 2 4
1 3 2
【样例输出2】
No answer
【解释】
需要使用最短路算法,这个算法有很多种,这里只介绍dijkstra算法的做法。
1、dijkstra算法核心还是贪心,每次都选择最优的点去更新下一个点,用样例解释一下
5 4
1 5 4
1 2 2
2 5 2
4 1 1
(1) 起初,有一个数组d[6]={999,0,999,999,999,999},999代表这个点不可到达,d[1]=0,代表点1与点1的距离是0
(2) 开始,可以从点1到达点2和点5,更新数组d,此时,d[6]={999,0,2,999,999,4},点1到点2的距离是2,到点5的距离是4
(3) 点1已经使用过了,所以不能再次使用(因为再用已经没有意义了,这个点已经不可能贡献出更好的走法),所以剩下的点中选择离点1最近的点再做相同的操作
(4) 最优的点是2,可以从点2到达点5,更新d数组,d[6]={999,0,2,999,999,4},同样地,点2后面就不能再被使用了
(5) 最优的点是5,不能从点5到达任何点,结束,那么所有点与点1的距离就是d[6]={999,0,2,999,999,4}所表示的值
那么如何记录最短路的方案数呢?
(1) 只需要在求最短的时候额外记录一下数据就可以了,例如以上样例,有一个数组,cnt[6]={0,1,0,0,0,0,0},cnt[i]的意思的走到点i最短路的数量是cnt[i]的值
(2)如果最短距离变小了,对应的点方案数置0,重新计算,如果距离不变,那么直接累加,计算的公式是:如果从点1到点5,那么cnt[5]+=cnt[1],当然,要判断需不需要置0
(3) 点1跑了之后,cnt[6]={0,1,1,0,0,1}
(4) 点2跑了之后,cnt[6]={0,1,1,0,0,2}
跑完之后,计算出,点1到点5最短距离是4,有两种方案
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
vector<vector<int>> v[4000010]; //邻接矩阵存图
int ma[2010][2010]; //邻接表去重。。。其实可以直接用邻接表做
int d[2010]; //点1到其它点地最短距离
long long cnt[2010]; //最短距离方案数
priority_queue<vector<int>,vector<vector<int>>,greater<vector<int>>> q; //优先级队列
signed main(){
ios::sync_with_stdio(0); //10的6次方以上的数据用cin、cout需要加速,不然会超时
cin.tie(0);
cout.tie(0);
int n,m;
cin>>n>>m;
for(int i=0;i<2010;i++){ //初始化,所有的都没有边
for(int j=0;j<2010;j++){
ma[i][j]=INT_MAX/10;
}
}
for(int i=0;i<m;i++){
int u,v,c;
cin>>u>>v>>c;
ma[u][v]=min(ma[u][v],c); //去重,取最优值
}
for(int i=0;i<2010;i++){ //构建邻接表
for(int j=0;j<2010;j++){
if(ma[i][j]!=INT_MAX/10){
v[i].push_back({j,ma[i][j]});
}
}
}
for(int i=0;i<2010;i++){ //初始化,点1到其它点初始距离是个比较大的值,代表不可达,方案数初始化为0
d[i]=INT_MAX/10;
cnt[i]=0;
}
cnt[1]=1; //到点1默认方案数为1
d[1]=0; //点1和点1距离为0
q.push({0,1}); //初始添加点1
while(!q.empty()){ //dijkstra算法
vector<int> vv=q.top();
q.pop();
for(vector<int> vvv:v[vv[1]]){
if(d[vvv[0]]>vv[0]+vvv[1]){ //更加优秀的方案
d[vvv[0]]=vv[0]+vvv[1];
cnt[vvv[0]]=cnt[vv[1]]; //置0后再计算
q.push({d[vvv[0]],vvv[0]}); //新点添加到比较队列
}else if(d[vvv[0]]==vv[0]+vvv[1]){ //最短距离一样的方案
cnt[vvv[0]]+=cnt[vv[1]]; //直接增加
}
}
}
if(d[n]==INT_MAX/10){ //如果是最大值,代表点1没办法到达点n
cout<<"No answer"<<endl;
}else{ //打印结果
cout<<d[n]<<' '<<cnt[n]<<endl;
}
}
7-3 这可能是道签到题
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
Nomi 需要出一道数学题,但是考虑到TeX太难搞了,所以还是出简单点好了。目前已知:
Nomi 会给你两个他喜欢的整数 x 和 y ,告诉他 f(x,y) 的值是多少就可以了,就这么简单。
提示:
1、ϕ(n) 表示的是小于等于 n 和 n 互质的数的个数,比如说 ϕ(1)=1,ϕ(4)=2,ϕ(5)=4。
2、⌈n⌉ 表示的是对 n 向上取整。
【输入格式】
第一行,输入两个整数 t(1 ≤ t ≤ 105 ),表示后续输入 t 次询问。
后续 t 行,每行输入两个整数 x 和 y (0 ≤ x,y ≤ 109),表示每一次的询问。
【输出格式】
输出 t 行,每行一个整数表示 f(x,y)的结果 ,结果对109 +7 取模。
【样例输入】
2
2 3
1000 123456
【样例输出】
365
500400402
【解释】
这个题涉及的知识点如下
1、条件1,欧拉函数,分析数据量,只需要打出107内的欧拉表就可以了
2、条件2,值为1
3、条件3,矩阵乘法+快速幂,可以看下图理解:
那么可推导出公式:
由于y的数据范围是0 ≤ x,y ≤ 109,暴力算矩阵乘法会超时,需要使用快速幂
4、条件4,等比公式+除法取模+公比1特判,可以看下图理解:
可以看出很明显的一个等比数列,额外加上yy*f(x,0),另外注意除法取模+公比1特判就可以了
【代码】
#include<bits/stdc++.h>
#define int long long //定义int为long long 类型,贪方便而已
using namespace std;
const int N = 1e7+10;
int mod = 1e9+7;
int phi[N]; // phi[i] 表示 i 的欧拉函数值
int p[N], cnt; // 统计素数
int vis[N];
void init(){
phi[1] = 1; // 情况1,注意初始化!
for (int i = 2;i <= N;i ++) { // 线性筛 2~n
if (!vis[i]) { // 说明i是素数
phi[i] = i - 1; // 情况2
p[cnt++] = i;
}
for (int j = 0;j < cnt;j ++) {
if (i * p[j] > N) break;
vis[i * p[j]] = 1;
if (i % p[j] == 0) {
phi[i * p[j]] = phi[i] * p[j]%mod; // 情况3
break;
}
phi[i * p[j]] = phi[i] * (p[j] - 1)%mod; // 情况4
}
}
}
int x,y;
int matrFpow(int d){ //矩阵快速幂
d--;
vector<vector<int>> an={{1,0},{0,1}};
vector<vector<int>> v={{x,y},{1,0}};
vector<vector<int>> temp; //中间矩阵,防止原矩阵在计算时被修改
while(d){
if(d&1){
temp=an;
an[0][0]=temp[0][0]*v[0][0]+temp[0][1]*v[1][0];
an[0][0]%=mod;
an[0][1]=temp[0][0]*v[0][1]+temp[0][1]*v[1][1];
an[0][1]%=mod;
an[1][0]=temp[1][0]*v[0][0]+temp[1][1]*v[1][0];
an[1][0]%=mod;
an[1][1]=temp[1][0]*v[0][1]+temp[1][1]*v[1][1];
an[1][1]%=mod;
}
temp=v;
v[0][0]=temp[0][0]*temp[0][0]+temp[0][1]*temp[1][0];
v[0][0]%=mod;
v[0][1]=temp[0][0]*temp[0][1]+temp[0][1]*temp[1][1];
v[0][1]%=mod;
v[1][0]=temp[1][0]*temp[0][0]+temp[1][1]*temp[1][0];
v[1][0]%=mod;
v[1][1]=temp[1][0]*temp[0][1]+temp[1][1]*temp[1][1];
v[1][1]%=mod;
d/=2;
}
return (an[0][0]+an[0][1])%mod;
}
int fpow(int val,int d){ //正常的快速幂
int ans=1;
while(d){
if(d&1){
ans*=val;
ans%=mod;
}
d/=2;
val*=val;
val%=mod;
}
return ans;
}
int f(int i,int j){
if(i>=0&&j==0){ //条件1,欧拉函数
return phi[(i+100)/100];
}else if(i==0&&j==1){ //条件2
return f(0,0);
}else if(i==0&&j>=2){ //条件3,矩阵快速幂
return matrFpow(j);
}else if(i>0&&j>=1){ //条件4,等比公式+除法取模+公比1特判
int a1=x*matrFpow(y)%mod;
int q=y;
int n=j;
int ext=fpow(y,n)*phi[i/100+1]%mod;
if(q==1){ //公比为1的时候特判
return a1*n+ext;
}
return (((a1*((1-fpow(q,n)+mod)%mod)%mod*fpow(((1-q+mod)%mod),mod-2)%mod))%mod+ext)%mod;
}
}
signed main(){
init();
int t;
cin>>t;
while(t--){
cin>>x>>y;
cout<<f(x,y)<<endl; //调用f(i,j)函数
}
}
7-4 Nomi的计算器
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
Nomi 制作了一个计算器,打算给还在读十六年级的 Liukw 使用。但可惜的是,Nomi 在这方面显得不太聪明, 做出来的计算器保留了先乘除后加减和从左向右的二元计算特性,但是内置的计算方式却充满了bug。于是委托整天沉迷于测试工作的 Wugh 帮忙, Wugh 熟能生巧,三两下就判断出了计算器真正的计算方式。
计算方式如下:(等号左边是输入的表达式,右边是实际上的计算方式)
-
符号 + :a + b=a ⊕ b,其中 ⊕ 符号为按位异或运算。
-
符号 - :a - b = a + b
-
符号 * :a ∗ b=b / a
-
符号 / :a / b=a * b \sqrt{b} b
现在给定一个仅包含非负整数与 +,−,∗,/ 四种符号的表达式,计算并输出其结果。Nomi 不喜欢浮点数,所计算过程中的每一步只要存在浮点数,都只会保留整数部分。同时题目保证计算过程不会出现中间结果超出int范围或者发生除0的情况。
【输入格式】
第一行,一个算术表达式字符串 s (1 ≤ s.length ≤ 106)。
【输出格式】
输出一个整数,表示该计算器的计算结果。
【样例输入】
4-3+2*5/3
【样例输出】
5
【样例解释】
先计算 2∗5,真正的计算方式是 5/2=2,目前表达式为 4−3+2/3。
计算 2/3,真正的计算方式是 2 * 3 \sqrt{3} 3=2,目前的表达式为 4−3+2。
计算 4−3,真正的计算方式是 4+3=7,目前的表达式为 7+2。
计算 7+2,真正的计算方式是 7⊕2=5,所以结果为 5。
【解释】
计算器的本质并没有改变,只是实际的计算方式改变了,第一遍先处理乘法和除法,第二遍再处理加法和减法即可,具体可看代码理解
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
int main(){ //主函数
string s;
cin>>s;
vector<int> v;
vector<char> vo; //储存还没计算的符号
int num=0;
char c='+'; //上一个计算符号
for(int i=0;i<s.size();i++){
if(s[i]>='0'&&s[i]<='9'){ //如果是数字,转成真正的数值
num*=10;
num+=s[i]-'0';
}
if(s[i]=='+'||s[i]=='-'||s[i]=='*'||s[i]=='/'||i==s.size()-1){ //如果是符号,或者是最后一个元素,开始计算
if(v.size()==0){ //如果容器还没有数字,直接添加
v.push_back(num);
c=s[i]; //记录下次计算使用的符号
num=0;
continue;
}
if(c=='+'){ //加法先不计算
v.push_back(num); //记录第二遍计算需要使用的数值
vo.push_back('^'); //记录第二遍计算需要使用的符号
}else if(c=='-'){ //减法先不计算
v.push_back(num); //记录第二遍计算需要使用的数值
vo.push_back('+'); //记录第二遍计算需要使用的符号
}else if(c=='*'){ //计算乘法
v.back() = num / v.back(); //真正的计算方式
}else if(c=='/'){ //计算除法
v.back()*=(int)sqrt(num); //真正的计算方式
}
c=s[i]; //下一次计算使用的符号
num=0; //下次使用的数值置0
}
}
int ans=v[0];
for(int i=1;i<v.size();i++){ //按顺序计算最终结果即可
if(vo[i-1]=='^'){
ans^=v[i];
}else if(vo[i-1]=='+'){
ans+=v[i];
}
}
cout<<ans<<endl;
}
7-5 篮球二叉树
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
作为真 IKUN 的 Nomi 觉得二叉树的就像一堆中分堆在一起,于是开始研究如何构造一棵篮球二叉树来证明自己对 kun 的喜爱。Nomi 认为只有中分是不够的,还要有铁山靠重心和背带的特性。他觉得你也是真正的 IKUN,所有把构造的任务交给了你,所以把任务交给了你。现在需要你协助他构造这一棵篮球二叉树,使得满足以下所有特性:
-
中分特性:这是一棵深度为 n (1 ≤ n ≤ 106) 的满二叉树。
-
背带特性:所有节点的和为 m (1≤m≤106) 且每一个节点的值 ai (1 ≤ ai ≤ 106) 。
-
铁山靠重心特性:对于树中所有的非叶子节点值为ax ,它的左子节点值为 al 、右子节点值为ar ,满足 ar = a l + ax 。
如果 Nomi 能成功构造输出该二叉树,请按照节点编号的给出任何一种满足情况的篮球二叉树前序遍历。如果无法构造则直接输出 -1。
【输入格式】
第一行给出两个整数 n 和 m (1 ≤ n,m ≤ 106),分别表示存在二叉树的深度为 n 与所有节点的和 m。
【输出格式】
输出一行。如果能够构造,请给出任意一种能够满足条件的 n 个整数,分别表示节点前序遍历的值ai (1 ≤ ai ≤ 106 )。如果无法构造则直接输出 -1。
【样例输入1】
3 32
【样例输出1】
2 1 1 2 3 10 13
【样例输入2】
4 11
【样例输出2】
-1
【样例输入3】
3 12
【样例输出3】
-1
【解释】
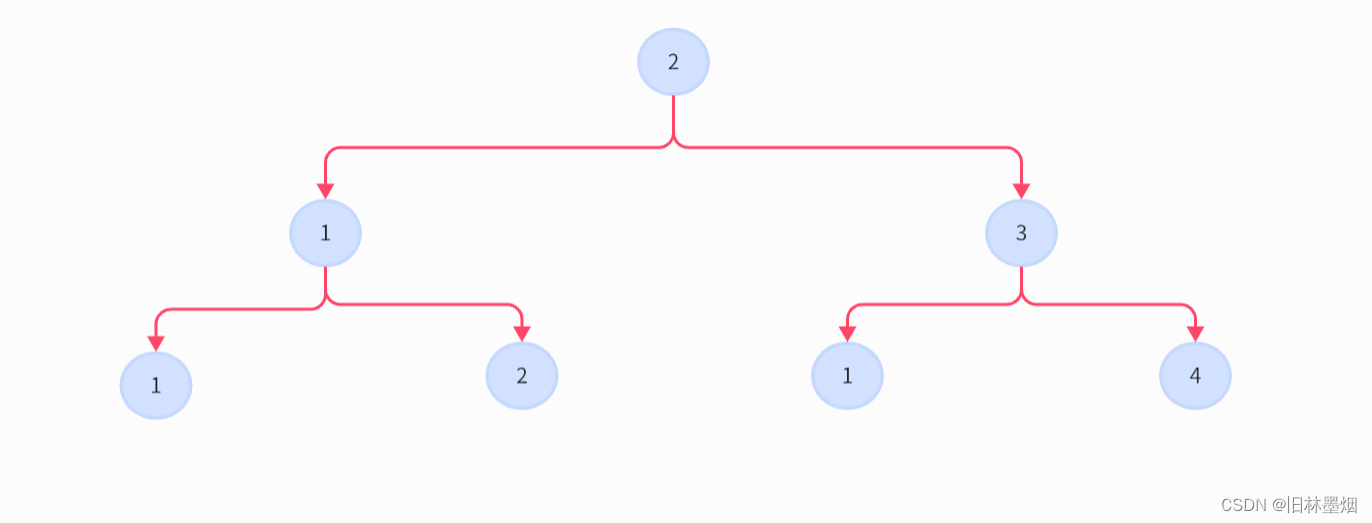
需要自己去思考如何最优地去构造这个二叉树,下面直接提供思路。
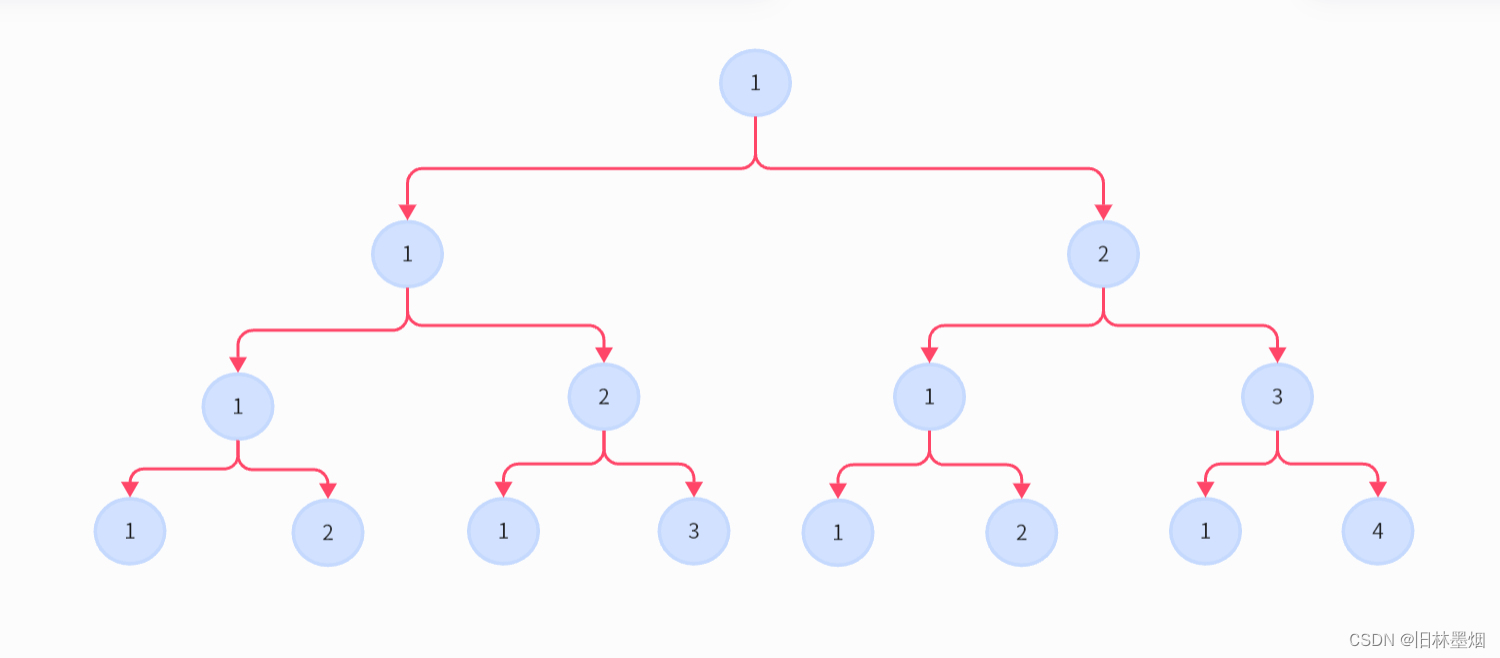
一棵深度为4且满足铁山靠重心特性的最小 (节点的总和最小) 满二叉树如下:
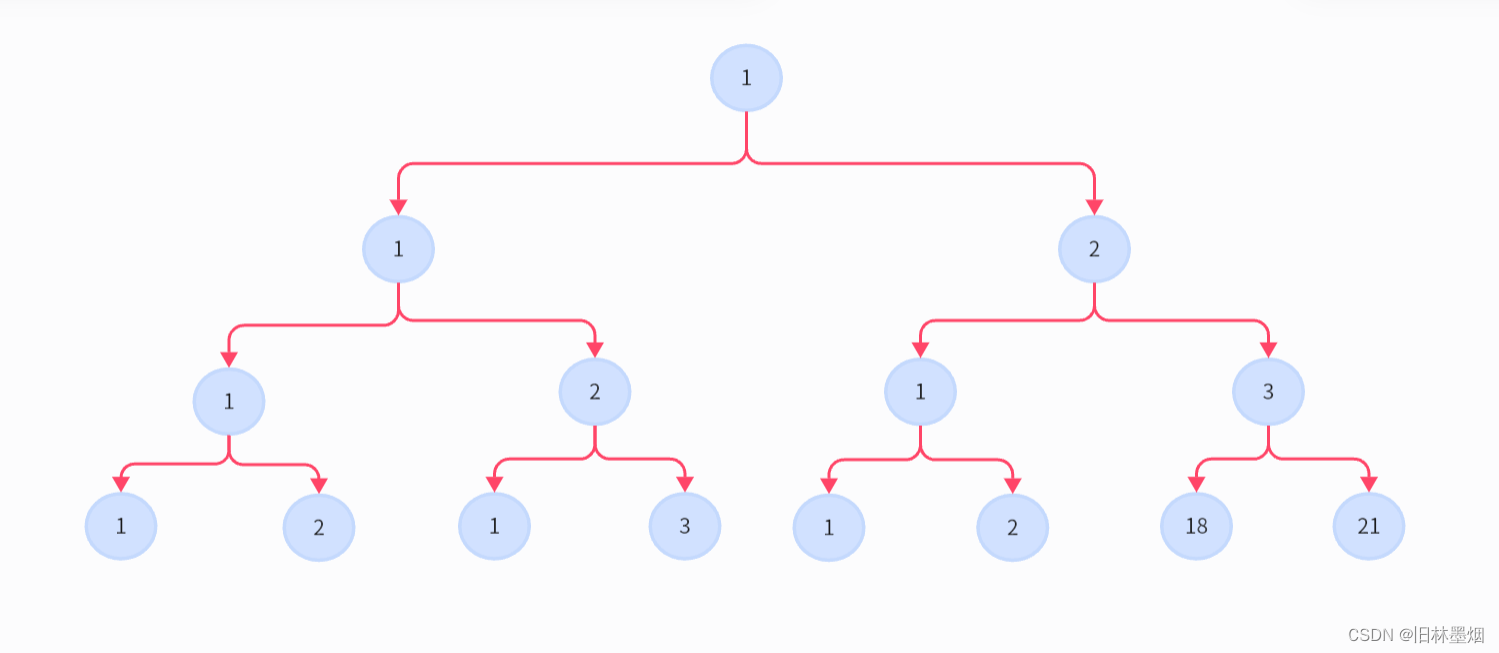
节点和为26,如果,m<26,那么篮球二叉树是没办法构成的,如果m=26,上面的树就是答案,如果,m=60,那么可以构成吗?可以的,看下图你就明白了
只需要在两个叶子节点补上(60-26)/2=17即可,类似的,像28、30、32、34、36、38这些,都可以用这个办法构造出来,那么奇数呢?39怎么构造?事实证明,只有深度为奇数,通过调整根节点,才可能出现奇数的情况。因为父节点+左子节点=右子节点,深度为偶数,永远不会出现奇数。
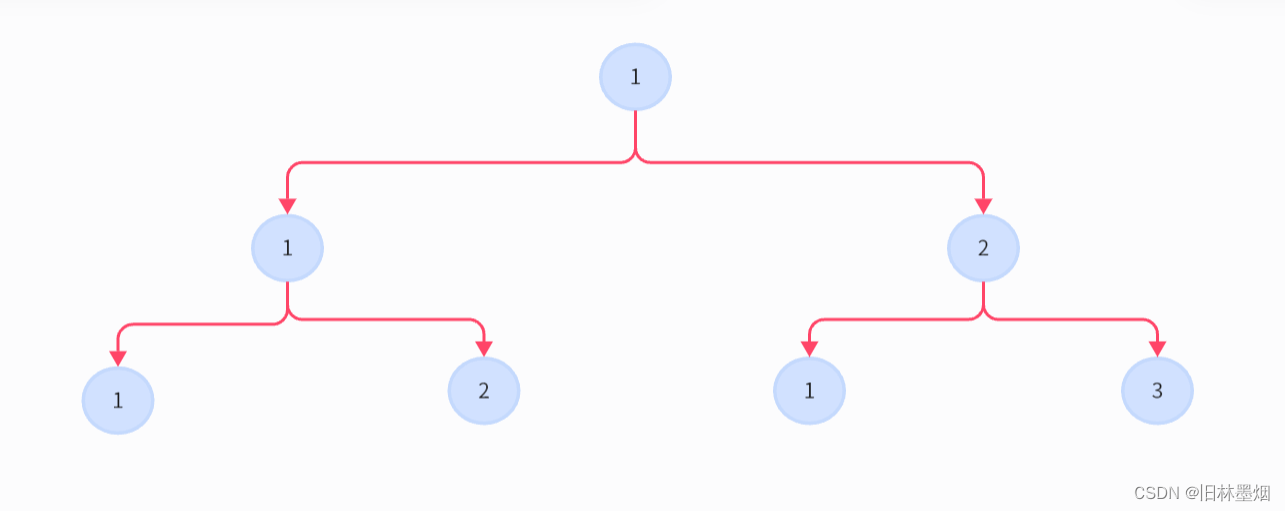
如果考虑的深度为3,最优的奇数构造方法:
最优的偶数构造方法:
可以看到,只要调整根节点的值为2,就可以切换奇偶性,这两种都是最优的构造方法,如果和不够,就可以通过调整两个叶子节点的值补满,如果和超出了,就表明不可构造。所以,只需要判断这两种方案是否可以构造出篮球二叉树就可以了
【代码】
#include<bits/stdc++.h>
using namespace std;
struct Tree{ //二叉树
int val,l,r,d;
}t[2000010];
int idu=0; //节点id
int sum=0; //节点总和
int f=1; //标记方案是否可行
int n,m;
void dfs(int id,int val,int d){ //构建总和最小、满足铁山靠重心特性的满二叉树,判断是否可以满足背带特性
sum+=val;
if(sum>m){
f=0;
return;
}
t[id].val=val;
t[id].d=d;
if(d+1<=n){ //高度不够,继续递归
t[id].l=++idu; //分配编号
t[id].r=++idu; //分配编号
dfs(t[id].l,1,d+1); //左子节点值为1
dfs(t[id].r,val+1,d+1); //右子节点值为当前节点值+1
}
}
int flag;
void prin(int ind,int d){ //前序打印二叉树
if(flag==1){
cout<<' ';
}
flag=1;
cout<<t[ind].val;
if(d+1<=n){
prin(t[ind].l,d+1);
prin(t[ind].r,d+1);
}
}
int main(){
cin>>n>>m;
if(n==1){ //高度为1,直接特判
cout<<m<<endl;
return 0;
}
if(n>20){ //高度超过20,一定不可以构成,因为每个节点的值至少为1,高度为20的满二叉树节点数超过了10的6次方
cout<<-1<<endl;
return 0;
}
dfs(0,1,1);
if(f==1&&(m-sum)%2==0){ //根节点为1是否可以构建篮球二叉树
t[(1<<n)-2].val+=(m-sum)/2; //和不够,叶子节点补齐
t[(1<<n)-3].val+=(m-sum)/2; //和不够,叶子节点补齐
prin(0,1);
return 0;
}
f=1; //初始化
idu=0;
sum=0;
dfs(0,2,1);
if(f==1&&(m-sum)%2==0){ //根节点为2是否可以构建篮球二叉树
t[(1<<n)-2].val+=(m-sum)/2; //和不够,叶子节点补齐
t[(1<<n)-3].val+=(m-sum)/2; //和不够,叶子节点补齐
prin(0,1);
return 0;
}
cout<<-1<<endl; //都不可以,打印-1
}
7-6 回文文回
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
给一个仅由小写字母组成的字符串S,有q次操作。
操作有以下两种类型:
“1 x c” 将位置x的字符修改为字符c。
“2 L R” 询问 s[L : R] 是否是回文串,如果是,输出"Yes",否则输出"No"。
【输入格式】
第一行输入两个整数 n, q,代表字符串的长度和操作的次数。 (1 ≤ n ≤ 106 ,1 ≤ q ≤ 105)
第二行输入字符串 S,代表初始的字符串。(1 ≤ ∣S∣ ≤ 106)
接下来 q 行,每一行输入一个 op,代表操作的类型。(1 ≤ op ≤ 2)
如果 op 为1,则输入一个整数 x 和一个字符 c,表示将位于 x 处的字符修改为字符 c。(1 ≤ x ≤ n,c为小写字母)
如果 op 为2,则输入两个整数 L,R,代表查询的区间。(1 ≤ L ≤ R ≤ n)
【输出格式】
对于每次op为2的操作,在单独一行中输出 “Yes” 或 “No”。
【样例输入】
7 8
abcbacb
2 1 5
2 4 7
2 2 2
1 5 c
2 1 5
2 4 7
1 4 c
2 3 6
【样例输出】
Yes
No
Yes
No
Yes
Yes
【解释】
首先将回文看成是正向的数字(hash),比如对ababacb在base为3的情况下,分别用1、2、3代表a、b、c,正序值为是1212132。然后我们将字符串逆序,也就是bcabcba,即逆序值为2312121。假如我们此时查询区间[1,5],等价于检查abcba是不是回文,在正序中有高五位为12121,逆序中有低五位为12121,12121=12121,证明hash的数值相同,即正反序代表的字符串是相同的(该区间就是回文)。
由于看hash值的区段值,所以与一般的回文奇偶性是无关的,可以抛开以往回文的概念。那么由于区间问题,涉及到简单的单点修改,我们可以尝试用线段树去维护两棵线段树,分别维护整一个字符串的正序和反序的hash值,单点修改某一个数,区间查询字符串区间代表的hash值即可。
由于hash碰撞,在字符串大与能够使用的最大数(unsigned long long最大值)的情况下,由于计算的溢出,可能出现相同的hash值代表了不同的字符串,所以只能说明答案正确的不一定正确,而答案错误的一定是错误的。
【代码】
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 1000005;
const ll base = 1e9+7; //hash基础值,最好是质数
unsigned ll pf[N];
int n,m;
string s;
struct node{
int l,r;
unsigned ll v;
};
struct tree { //线段树
node tr[N<<2];
void up(int p){ //懒加载
int mid=(tr[p].l+tr[p].r)>>1;
tr[p].v = tr[p<<1].v*pf[tr[p].r-mid]+tr[p<<1|1].v;
}
void build(int p,int l,int r,bool rv){ //初始化
tr[p].l=l;
tr[p].r=r;
if(l==r){
if(!rv)tr[p].v=s[l]-'a'+1;
else tr[p].v=s[n-l+1]-'a'+1;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid,rv);
build(p<<1|1,mid+1,r,rv);
up(p);
}
void modify(int p,int l,int r,int x){ //修改
if(tr[p].l==l&&tr[p].r==r){
tr[p].v=x;
return;
}
int mid=(tr[p].l+tr[p].r)>>1;
if(l<=mid)modify(p<<1,l,r,x);
else modify(p<<1|1,l,r,x);
up(p);
}
unsigned ll query(int p,int l,int r){ //查询
if(tr[p].r<l||tr[p].l>r){
return 0;
}
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].v*pf[r-tr[p].r];
}
int mid=(tr[p].l+tr[p].r)>>1;
unsigned ll r1=query(p<<1,l,r);
unsigned ll r2=query(p<<1|1,l,r);
return r1 + r2;
}
}t1,t2;
int main(){
pf[0]=1;
for(int i=1;i<=1000001;i++){
pf[i] = pf[i-1]*base;
}
cin>>n>>m;
cin>>s;
s="#"+s;
t1.build(1,1,n,0); //一棵正序的树
t2.build(1,1,n,1); //一棵反转后的树
int w,x;
string y;
while(m--){
cin>>w>>x;
if(w==1){
cin>>y;
int p = y[0]-'a'+1;
t1.modify(1,x,x,p); //两颗树同时修改
t2.modify(1,n-x+1,n-x+1,p); //两颗树同时修改
}else{
cin>>w;
if(t1.query(1,x,w)==t2.query(1,n-w+1,n-x+1)){ //判断正序和反转后的字符串hash值是否一致
cout<<"Yes"<<endl;
}
else{
cout<<"No"<<endl;
}
}
}
}
7-7 求和游戏
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
Wugh和 Liukw 在用卡牌玩游戏,Yisr在旁边观战。每一场游戏开始时,每张卡牌上有一个正整数a i ,他们将卡牌摊开正面朝上,游戏包括以下两个步骤:
- 第一步,Wugh 可以用魔法将卡牌中至多 k 张卡牌从世界上消失。
- 第二步,Liukw 可以用魔法将卡牌中至多 x 张卡牌的数乘以 -1。
Wugh 希望最大化剩余卡牌的和,Liukw 则希望最小化剩余卡牌的和。双方都采用最优的策略进行游戏,那么你能帮助 Yisr 提前预知游戏最后剩下的卡牌和是多少吗?
【输入格式】
第一行,输入一个正整数 t (1 ≤ t ≤ 105),表示游戏次数。
对于每一场游戏:
第一行,包含三个正整数 n, k , x (1 ≤ n ≤ 2∗105,1 ≤ k,x ≤ n),n 表示初始卡牌的个数,k 和 x 的含义与题目描述一致。
第二行,包含 n 个正整数 ai (1 ≤ ai ≤ 1000),表示每一张卡牌上面的数值。
题目保证,对于所有游戏,n 的总和不会超过 2∗10 5 。
【输出格式】
对于每个样例,输出一个整数,代表最终剩余卡牌的总和。
【样例输入】
8
1 1 1
1
4 1 1
3 1 2 4
6 6 3
1 4 3 2 5 6
6 6 1
3 7 3 3 32 15
8 5 3
5 5 3 3 3 2 9 9
10 6 4
1 8 2 9 3 3 4 5 3 200
2 2 1
4 3
2 1 2
1 3
【样例输出】
0
2
0
3
-5
-9
0
-1
【解释】
很容易看出来的贪心性质,由于卡牌上的数值只会是正数,那么Liukw一定会尽可能地选择数值最大、数量最多的卡牌乘以-1。实际上,剩余卡牌的和就取决Wugh的选择了,如果Wugh要拿走x张牌,那么他一定会拿走前x大的牌。
只要枚举Wugh拿走牌的数量就可以了。
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
int main(){
int t;
cin>>t;
while(t--){
int n,a,b;
cin>>n>>a>>b;
vector<int> v; //卡牌数组
for(int i=0;i<n;i++){
int va;
cin>>va;
v.push_back(va);
}
sort(v.begin(),v.end()); //小到大排序
deque<int> qa; //去掉卡牌数组
deque<int> qb; //乘以负1数组
int sum=0; //最后剩余卡牌的和
while(v.size()>0&&a>0){ //先尽可能去掉总和更多牌
a--;
qa.push_back(v.back());
v.pop_back();
}
while(v.size()>0&&b>0){ //尽可能使总和更多的牌乘以-1
b--;
qb.push_back(v.back());
sum-=v.back(); //乘以-1的牌就要减去
v.pop_back();
}
for(int c:v){ //没使用的牌直接累加
sum+=c;
}
int ans=sum;
while(!qa.empty()){ //枚举让卡牌消失的数量
qb.push_front(qa.back()); //a即将出队的卡牌,b需要将其乘以-1,因为a数组的里元素的值永远大于b的
sum-=qa.back();
b--;
if(b<0){ //如果乘以-1的卡牌数量超出了限制,就需要去掉最小的那张
sum+=2*qb.back();
qb.pop_back();
b++;
}
qa.pop_back(); //出队最小的卡牌,消失的卡牌数量-1
ans=max(ans,sum);
}
cout<<ans<<endl;
}
}
7-8 得分王
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
一个 n 行 m 列的方格图,图中会出现"0",“#”,"S"三种字符:
- "0"代表该位置能走
- "#"代表该位置不能走
- "S"代表初始位置
你初始站在位置在 S 上,初始分值为 1。
图中会有 k 个得分点,得分点只会出现在给定地图的 “0” 的位置上,且同一个位置上不会出现多于一个得分点。
请输出从初始位置出发,不限步数,能够得到的最大得分。
得分点定义:得分点是一次性的。经过得分点后,分值立刻发生变化,得分点立刻消失,再次经过该得分点所在位置时不对分数造成任何影响。即当你的当前坐标首次与得分点所在坐标重合时,你的分值就会立刻变化,再次经过该点时对分值不造成任何影响。
注意:过程中不可以越过任何一个得分点。
【输入格式】
第一行输入 n,m。表示该方格图有 n 行 m 列。(1 ≤ n,m ≤ 8)
接下来 n 个字符串表示方格图。
然后是一个整数 k ,代表一共有 k 个得分点。(0 ≤ k ≤ min(8,n∗m) )
接下来 k 行,每行 4 个整数 x,y,t,v。 (1 ≤ x ≤ n, 1 ≤ y ≤ m, 1 ≤ t ≤ 2, 1 ≤ v ≤ 50)
x,y 代表该得分点位于第 x 行第 y 列。
t 代表得分类型(1表示加法,2表示乘法)
v 代表分值。
【输出格式】
在一行中输出最大得分。
【样例输入1】
1 5
00S00
2
1 1 1 5
1 5 2 2
【样例输出1】
12
【样例输入2】
3 5
00S00
000##
00000
4
1 1 1 5
1 5 2 2
3 3 2 3
3 5 1 10
【样例输出2】
56
【样例说明】
样例2一种最优的走法是,先到 (1,1),再到 (3,3),然后到 (3,5),最后到 (1,5),得到的分数((1+5)∗3+10)∗2=56
【解释】
深搜+广搜,数据量比较小,暴力所有情况即可
【代码】
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m;
string s[8];
ll v[8][8]={0};
ll d[8][8][2]={0};
int f[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
int a[72][72];
int idx[72],id=1,mod[72];
int px=0;
int x0=-1,yy0;
int dfs(int x,int y){
if(x<0||x>=n||y<0||y>=m){
return 0;
}
if(d[x][y][0]==2){
if(v[x][y]==0){
v[x][y]=id+px;
idx[id+px]=d[x][y][1];
a[id][id+px]=1;
a[id+px][id]=1;
mod[id+px]=2;
px++;
}
else{
a[id][v[x][y]]=1;
a[v[x][y]][id]=1;
}
return 0;
}
if(v[x][y]!=0){
return 0;
}
v[x][y]=id;
ll res=d[x][y][1];
for(int i=0;i<4;i++){
int xx = x+f[i][0];
int yy = y+f[i][1];
if(xx>=0&&yy>=0&&xx<n&&yy<m){
if(s[xx][yy]!='#'){
res+=dfs(xx,yy);
}
}
}
return res;
}
bool vp[72];
void dfs2(int p){
if(vp[p])return;
vp[p]=1;
for(int i=0;i<id;i++){
if(a[p][i]){
dfs2(i);
}
}
}
ll ck(vector<int> &num){
bool vis[72]={0};
vis[v[x0][yy0]]=1;
ll res=0;
for(int i=0;i<num.size();i++){
if(!vp[num[i]])continue;
if(!vis[num[i]]){
return 0;
}
if(mod[num[i]]==1){
res+=idx[num[i]];
}
else{
res*=idx[num[i]];
}
for(int j=0;j<id;j++){
if(a[num[i]][j]){
vis[j]=1;
}
}
}
return res;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>s[i];
for(int j=0;x0==-1&&j<m;j++){
if(s[i][j]=='S'){
x0=i;
yy0=j;
}
}
}
int t;
cin>>t;
int x,y;
for(int i=0;i<t;i++){
cin>>x>>y;
x--;
y--;
cin>>d[x][y][0];
cin>>d[x][y][1];
}
d[x0][yy0][1]+=1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(v[i][j]==0&&s[i][j]!='#'){
px=1;
mod[id]=1;
idx[id]=dfs(i,j);
id+=px;
}
}
}
vector<int> nums;
dfs2(v[x0][yy0]);
for(int i=1;i<id;i++){
nums.push_back(i);
}
ll ans=1;
do {
ans=max(ans,ck(nums));
} while (next_permutation(nums.begin(), nums.end()));
cout<<ans<<endl;
}
7-9 玛恩纳
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
茶余饭后,Nomi 像往常一样打开了粥,无意间看到有玛恩纳的池子,看着包里仅剩下的几张寻访凭证,无脑的随便抽了一下,没想到三发就把玛恩纳给搞到了。喜出望外的 Nomi 掏出了仓库仅剩下的作战记录把玛恩纳直接精二了,迫不及待地跑到7-18去试一下三技能强度。
Nomi 认识到玛恩纳的强大,没有任何敌人能够抵挡住玛恩纳的一次攻击,此次每个地图都将带上玛恩纳,成为MaBaoNan。
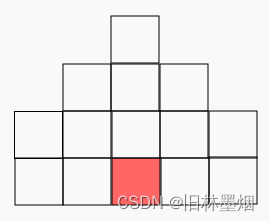
玛恩纳三技能的攻击范围(方向朝上)如下,一共覆盖了14格(包括他本体所在的位置也能够攻击),同时玛恩纳的攻击方向是可以90度旋转的(也就是所存在上下左右四个方向的放置方式)。图中红色的是玛恩纳本体的位置,玛恩纳本体在地图中不能够位于障碍物上,而且不能够超出地图的范围。目前已知地图的大小为 n*m (1 ≤ n∗m ≤106 ,0 ≤ i ≤ n,0 ≤ j ≤ m),地图中可能存在障碍物ai,j (ai,j = −1,障碍物不会受到攻击) 和血量为 ai,j (0 ≤ ai,j ≤ 109) 的敌人。由于玛恩纳导致游戏难度太低了,每个地图 Nomi 都只会将玛恩纳部署到合适的位置一次(保证绝对可以部署),使得他能够攻击到的敌人血量之和最大。
【输入格式】
第 一 行输入两个整数n,m (1 ≤ n∗m ≤ 106),n表示地图的行数,m表示地图的列数。
第二到 n+1 行,每行都存在 m 个整数 ai,j (−1 ≤ ai,j ≤ 109),ai,j = −1 时表示当前位置为障碍物,其他整数则表示当前位置敌人的血量。
【输出格式】
第一行输出一个大写字母表示玛恩纳的攻击方向 (向上输出‘U’,向下输出‘D’,向左输出‘L’,向右输出‘R’)。
第二行输出一个整数表示玛恩纳攻击的敌人最大血量之和。
第三行分别输出两个整数表示玛恩纳的坐标 i 和 j (0 ≤ i < n,0 ≤ j < m)。
注意:同时存在最大血量之和时,坐标 i 尽可能小。i 相同时,坐标 j 尽可能小。i,j 相同时且存在多个方向都满足时,方向优先级按上、下、左、右的优先顺序即可。
【样例输入】
6 10
-1 0 -1 0 -1 -1 0 0 0 -1
0 -1 -1 -1 -1 -1 0 -1 -1 0
0 -1 0 -1 0 -1 9999 -1 -1 0
0 -1 0 -1 0 -1 1 0 -1 -1
0 -1 88 -1 0 -1 0 0 -1 -1
2 -1 90 -1 1 -1 0 -1 -1 -1
【样例输出】
D
10001
2 4
【解释】
模拟题,根据题目意思暴力枚举每一个条件,取最优的答案即可。
1、一个比较好的实现方法,就是打方向表,这样看起来比较直观,容易排bug,不用写那么多if else语句,具体可以看代码实现
2、输出的结果有优先顺序,实现的时候注意枚举的顺序就行了
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
int n,m;
vector<vector<long long>> v; //动态存地图
int fu[14][2]={ //向上的方向表,(0,0)代表玛恩纳的位置,其它13格是相对玛恩纳的位移
{-3,0},
{-2,-1},{-2,0},{-2,1},
{-1,-2},{-1,-1},{-1,0},{-1,1},{-1,2},
{0,-2},{0,-1},{0,0},{0,1},{0,2}
};
int fd[14][2]={ //向下的方向表
{3,0},
{2,-1},{2,0},{2,1},
{1,-2},{1,-1},{1,0},{1,1},{1,2},
{0,-2},{0,-1},{0,0},{0,1},{0,2}
};
int fl[14][2]={ //向左的方向表
{-2,0},{-2,-1},
{-1,0},{-1,-1},{-1,-2},
{0,0},{0,-1},{0,-2},{0,-3},
{1,0},{1,-1},{1,-2},
{2,0},{2,-1},
};
int fr[14][2]={ //向右的方向表
{-2,0},{-2,1},
{-1,0},{-1,1},{-1,2},
{0,0},{0,1},{0,2},{0,3},
{1,0},{1,1},{1,2},
{2,0},{2,1},
};
long long getU(int x,int y){ //获取向上方向造成的伤害
long long sum=0;
for(int i=0;i<14;i++){ //根据方向表找到所有能攻击到的位置
int xx=x+fu[i][0];
int yy=y+fu[i][1];
if(xx>=0&&xx<n&&yy>=0&&yy<m&&v[xx][yy]!=-1){ //攻击的地方不能超出地图,并且不能是障碍物
sum+=v[xx][yy];
}
}
return sum;
}
long long getD(int x,int y){ //获取向下方向造成的伤害
long long sum=0;
for(int i=0;i<14;i++){ //根据方向表找到所有能攻击到的位置
int xx=x+fd[i][0];
int yy=y+fd[i][1];
if(xx>=0&&xx<n&&yy>=0&&yy<m&&v[xx][yy]!=-1){ //攻击的地方不能超出地图,并且不能是障碍物
sum+=v[xx][yy];
}
}
return sum;
}
long long getL(int x,int y){ //获取向左方向造成的伤害
long long sum=0;
for(int i=0;i<14;i++){ //根据方向表找到所有能攻击到的位置
int xx=x+fl[i][0];
int yy=y+fl[i][1];
if(xx>=0&&xx<n&&yy>=0&&yy<m&&v[xx][yy]!=-1){ //攻击的地方不能超出地图,并且不能是障碍物
sum+=v[xx][yy];
}
}
return sum;
}
long long getR(int x,int y){ //获取向右方向造成的伤害
long long sum=0;
for(int i=0;i<14;i++){ //根据方向表找到所有能攻击到的位置
int xx=x+fr[i][0];
int yy=y+fr[i][1];
if(xx>=0&&xx<n&&yy>=0&&yy<m&&v[xx][yy]!=-1){ //攻击的地方不能超出地图,并且不能是障碍物
sum+=v[xx][yy];
}
}
return sum;
}
int main(){
cin>>n>>m;
char dir='\0'; //方向
long long ansX=-1,ansY=1,ans=0; //分别是坐标x、坐标y、总伤害
for(int i=0;i<n;i++){ //存地图
vector<long long> vv;
for(int j=0;j<m;j++){
long long a;
cin>>a;
vv.push_back(a);
}
v.push_back(vv);
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(v[i][j]!=-1){ //不能放置在障碍物位置
if(getU(i,j)>ans){ //注意枚举顺序,上下左右
dir='U';
ans=getU(i,j);
ansX=i;
ansY=j;
}
if(getD(i,j)>ans){
dir='D';
ans=getD(i,j);
ansX=i;
ansY=j;
}
if(getL(i,j)>ans){
dir='L';
ans=getL(i,j);
ansX=i;
ansY=j;
}
if(getR(i,j)>ans){
dir='R';
ans=getR(i,j);
ansX=i;
ansY=j;
}
}
}
}
cout<<dir<<endl; //打印结果
cout<<ans<<endl;
cout<<ansX<<' '<<ansY<<endl;
}
7-10 涂矩阵
时间限制: 1.0s 内存限制:256.0MB
【问题描述】
Liukw 给你一个 n × m 的矩阵,矩阵中存在 R、G、Y 三种颜色,你需要使矩阵满足以下条件:
给你一个 n × m 的矩阵,让你使矩阵满足以下条件:
1、从最上方开始若干行(最少一行)的格子全是红色(用 R 表示);
2、接下来若干行(至少一行)的格子全是绿色(用 G 表示);
3、剩下的行(至少一行)的格子全是黄色(用 Y 表示)。
现在给你一个 n 行 m 列的矩阵,且每个格子的颜色为红色、绿色、黄色之一,你可以对矩阵的每个格子进行修改颜色,每次修改可以将矩阵的任意一个格子改成你想要的颜色,现在希望将这个矩阵变成满足上述条件,问你最少需要多少次修改操作。
【输入格式】
第一行两个整数 n (3 ≤ n ≤ 1000), m (1 ≤ m ≤ 1000)
接下来 n 行,每行 m 个字符,矩阵的每一个格子是 R (红色),G (绿色),Y (黄色) 中的一个。
【输出格式】
输出一个整数,表示最少需要修改多少块。
【样例输入】
4 5
RGYRG
YGRRY
GRYYR
YGYRG
【样例输出】
13
【解释】
1、106 数据直接暴力枚举是行不通,仔细分析容易发现,可以压缩每一行的数据,例如RGYRGGGGG可以用2个红色、6个绿色、1个黄色来表示,即使再多的数据,也只用数值来表示。因为题目求的是需要修改的次数,那么,可以记录刷成红色需要7次、刷成绿色需要3次、刷成黄色需要8次
2、数据压缩后可以暴力枚举红色行的数量、绿色行的数量、黄色行的数量来计算所有情况需要修改的次数,取最小值即可
3、需要使用前缀和 + 差分的技巧在O(1)的时间复杂度内计算指定情况修改的次数
前缀和与差分算法:
前缀和与差分算法主要是为了快速求出某个区间的和,例如有一个数组a[10]={0,1,2,3,4,5,6,7,8,9},我们需要求a[3]到a[7]的和,传统的办法是求a[3]+a[4]+a[5]+a[6]+a[7],但是这样求复杂度是O(n),如果我们建立了一个前缀数组S[9]={a[0],a[0]+a[1],a[0]+a[1]+a[2],a[0]+a[1]+a[2]+a[3],……,a[0]+a[1]+……+a[9]},那么我们要求a[3]到a[7]的和可以用差分思想S[7]-S[2]即可求出
【代码】
#include<bits/stdc++.h> //万能头文件
using namespace std; //命名空间
int main(){ //主函数
int n,m;
cin>>n>>m;
int r[1010]={0}; //每一行刷成红色需要的修改次数,例如,r[2]的值代表第二行全刷成红色需要的修改次数
int g[1010]={0}; //每一行刷成绿色需要的修改次数
int y[1010]={0}; //每一行刷成黄色需要的修改次数
for(int i=1;i<=n;i++){
string s;
cin>>s;
for(int j=0;j<s.size();j++){ //记录每一行刷成不同颜色各需要的修改次数
if(s[j]!='R'){
r[i]++;
}
if(s[j]!='G'){
g[i]++;
}
if(s[j]!='Y'){
y[i]++;
}
}
r[i]+=r[i-1]; //做前缀和操作
g[i]+=g[i-1];
y[i]+=y[i-1];
}
int ans=INT_MAX;
for(int i=1;i<=n-2;i++){ //1值i行刷成红色
for(int j=i+1;j<=n-1;j++){ //i+1至j行刷成绿色,剩下j+1至n行刷成黄色
ans=min(ans,r[i]+g[j]-g[i]+y[n]-y[j]); //差分直接计算结果
}
}
cout<<ans<<endl; //打印结果
}