本讲将讨论“机器人如何观测外部世界”,也就是观测方程部分。而在以相机为主的视觉SLAM中,观测主要是指相机成像的过程。
三维世界中的一个物体反射或发出的光线,穿过相机光心后,投影在相机的成像平面上。相机的感光器件接收到光线后,产生测量值,就得到了像素,形成了我们见到的照片。
相机将三维世界中的坐标点(单位为米)映射到二维图像平面(单位为像素)的过程能够用一个几何模型进行描述。这个模型有很多种,其中最简单的称为针孔模型。
在本讲中我们用一个简单的针孔相机模型来对这种映射关系进行建模。同时,由于相机镜头上的透镜的存在,使得光线投影到成像平面的过程中会产生畸变。因此,我们使用针孔和畸变两个模型来描述整个投影过程,这两个模型构成相机的内参数。
针孔相机模型
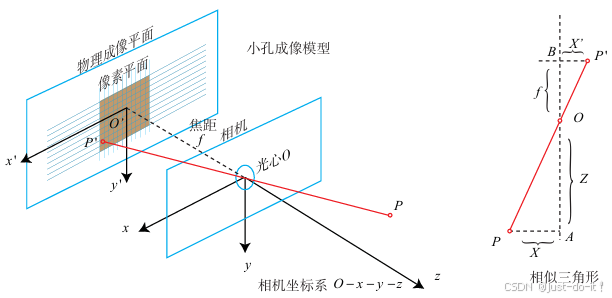
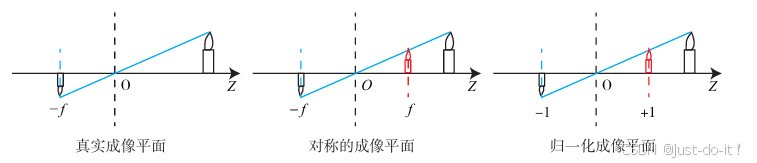
现在来对这个简单的针孔模型进行几何建模。设 O − x − y − z O-x-y-z O−x−y−z为相机坐标系,习惯上我们让 z z z轴指向相机前方, x x x向右, y y y向下(此图我们应该站在左侧看右侧)。 O O O为摄像机的光心,也是针孔模型中的针孔。现实世界的空间点 P P P,经过小孔投影 O O O之后,落在物理成像平面 O ′ − x ′ − y ′ O'-x' -y' O′−x′−y′上,成像点为 P ′ P' P′。设 P P P的坐标为 [ X , Y , Z ] T [X,Y,Z]^{T} [X,Y,Z]T, P ′ P' P′为 [ X ′ , Y ′ , Z ′ ] T [X',Y',Z']^{T} [X′,Y′,Z′]T,并且设物理成像平面到小孔的距离为 f f f(焦距)。为了让模型更符合实际,我们可以等价地把成像平面对称地放到相机前方,和三维空间点一起放在摄像机坐标系的同一侧。
那么,根据三角形相似关系,有:
Z f = X X ′ = Y Y ′ \frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}} fZ=X′X=Y′Y
把 X ′ , Y ′ X',Y' X′,Y′放到等式左侧,整理得:
X ′ = f X Z Y ′ = f Y Z \begin{aligned} & X^{\prime}=f \frac{X}{Z} \\ & Y^{\prime}=f \frac{Y}{Z}\end{aligned} X′=fZXY′=fZY
还需要在成像平面上对像进行采样和量化。为了描述传感器将感受到的光线转换成图像像素的过程,我们设在物理成像平面上固定着一个像素平面 o − u − v o-u-v o−u−v。我们在像素平面得到了 P ′ P' P′的像素坐标: [ u , v ] T [u,v]^{T} [u,v]T。
像素坐标系通常的定义方式是:原点 o ′ o' o′位于图像的左上角, u u u轴向右与 x x x轴平行, v v v轴向下与 y y y轴平行。像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。我们设像素坐标 u u u在轴上缩放了 α \alpha α倍,在 v v v上缩放了 β \beta β倍。同时,原点平移了 [ c x , c y ] T [c_{x} ,c_{y} ]^{T} [cx,cy]T。那么, P ′ P' P′的坐标与像素坐标 [ u , v ] T [u,v]^{T} [u,v]T的关系为:
{ u = α X ′ + c x v = β Y ′ + c y \left\{\begin{array}{l}u=\alpha X^{\prime}+c_x \\ v=\beta Y^{\prime}+c_y\end{array}\right. {u=αX′+cxv=βY′+cy
代入上式 X ′ , Y ′ X',Y' X′,Y′,并把 α f \alpha f αf合并成 f x f_x fx,把 β f \beta f βf合并成 f y f_y fy,得:
{ u = f x X Z + c x v = f y Y Z + c y \left\{\begin{array}{l}u=f_x \frac{X}{Z}+c_x \\ v=f_y \frac{Y}{Z}+c_y\end{array}\right. {u=fxZX+cxv=fyZY+cy
把该式写成矩阵形式会更加简洁,不过左侧需要用到齐次坐标,右侧则是非齐次坐标:
( u v 1 ) = 1 Z ( f x 0 c x 0 f y c y 0 0 1 ) ( X Y Z ) ≜ 1 Z K P \left(\begin{array}{l}u \\ v \\ 1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{array}\right)\left(\begin{array}{l}X \\ Y \\ Z\end{array}\right) \triangleq \frac{1}{Z} \boldsymbol{K} \boldsymbol{P} uv1 =Z1 fx000fy0cxcy1 XYZ ≜Z1KP
该式中, K \boldsymbol{K} K称为相机的内参数矩阵。通常情况下,相机的内参在出厂时已固定,不会在使用过程中发生变化。有些厂商会提供相机的内参,而有时需要用户自行标定以确定内参。
有内参,自然也有外参。由于相机在运动,上式中使用的相机坐标系下的坐标 P \boldsymbol{P} P,其实是由相机在当前位姿下的世界坐标(记为 P w \boldsymbol{P_w} Pw)转换而来。相机的位姿由旋转矩阵 R \boldsymbol{R} R和平移向量 t \boldsymbol{t} t描述。所谓外参是将世界坐标系中的点转换到相机坐标系的外部参数。
Z P u v = Z [ u v 1 ] = K ( R P w + t ) = K T P w Z \boldsymbol{P}_{u v}=Z\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}_w+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}_w ZPuv=Z uv1 =K(RPw+t)=KTPw
投影过程还可以从另一个角度来看。我们可以把一个世界坐标点先转换到相机坐标系,再除掉它最后一维的数值(即该点距离相机成像平面的深度),这相当于把最后一维进行归一化处理,得到点 P P P在相机归一化平面上的投影:
( R P w + t ) = [ X , Y , Z ] T ⏟ 相机坐标 → [ X / Z , Y / Z , 1 ] T ⏟ 归一化坐标 \left(\boldsymbol{R} \boldsymbol{P}_w+\boldsymbol{t}\right)=\underbrace{[X, Y, Z]^{\mathrm{T}}}_{\text {相机坐标 }} \rightarrow \underbrace{[X / Z, Y / Z, 1]^{\mathrm{T}}}_{\text {归一化坐标 }} (RPw+t)=相机坐标 [X,Y,Z]T→归一化坐标 [X/Z,Y/Z,1]T
归一化坐标可看成相机前方 z = 1 z=1 z=1的平面上的一个点,这个 z = 1 z=1 z=1平面也称为归一化平面。归一化坐标再左乘内参就得到了像素坐标,所以我们可以把像素坐标 [ u , v ] T [u,v]^{T} [u,v]T看成对归一化平面上的点进行量化测量的结果。
畸变
为了获得好的成像效果,我们在相机的前方加了透镜。透镜的加入对成像过程中光线的传播会产生新的影响:一是透镜自身的形状对光线传播的影响,二是在机械组装过程中,透镜和成像平面不可能完全平行,这也会使得光线穿过透镜投影到成像面时的位置发生变化。
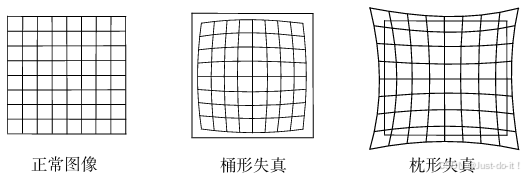
由透镜形状引起的畸变称为径向畸变。由于实际加工制作的透镜往往是中心对称的,这使得不规则的畸变通常径向对称。它们主要分为两大类:桶形畸变和枕形畸变。
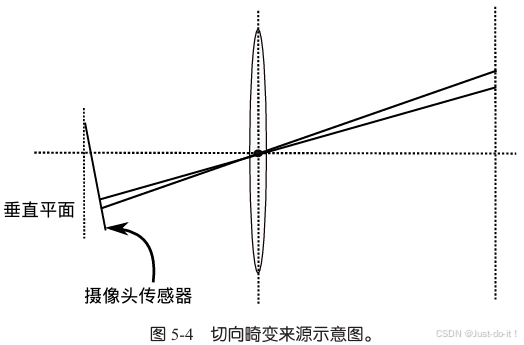
除了透镜的形状会引入径向畸变外,在相机的组装过程中由于不能使透镜和成像平面严格平行也会引入切向畸变。
通常假设径向畸变呈多项式关系(数学建模),即:
x distorted = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y distorted = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) \begin{aligned} & x_{\text {distorted }}=x\left(1+k_1 r^2+k_2 r^4+k_3 r^6\right) \\ & y_{\text {distorted }}=y\left(1+k_1 r^2+k_2 r^4+k_3 r^6\right)\end{aligned} xdistorted =x(1+k1r2+k2r4+k3r6)ydistorted =y(1+k1r2+k2r4+k3r6)
其中 [ x distorted , y distorted ] T [x_{\text {distorted }},y_{\text {distorted }}]^T [xdistorted ,ydistorted ]T是畸变后点的归一化坐标。另一方面,对于切向畸变,可以使用另外的两个参数 p 1 , p 2 p_1,p_2 p1,p2来进行纠正:
x distorted = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y distorted = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \begin{aligned} & x_{\text {distorted }}=x+2 p_1 x y+p_2\left(r^2+2 x^2\right) \\ & y_{\text {distorted }}=y+p_1\left(r^2+2 y^2\right)+2 p_2 x y\end{aligned} xdistorted =x+2p1xy+p2(r2+2x2)ydistorted =y+p1(r2+2y2)+2p2xy
因此,对于相机坐标系中的一点,我们能够通过5个畸变系数找到这个点在像素平面上的正确位置:
-
将三维空间点投影到归一化图像平面。设它的归一化坐标为 [ x , y ] T [x,y]^{T} [x,y]T。
-
对归一化平面上的点计算径向畸变和切向畸变。
{ x distorted = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y distorted = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \left\{\begin{array}{l}x_{\text {distorted }}=x\left(1+k_1 r^2+k_2 r^4+k_3 r^6\right)+2 p_1 x y+p_2\left(r^2+2 x^2\right) \\ y_{\text {distorted }}=y\left(1+k_1 r^2+k_2 r^4+k_3 r^6\right)+p_1\left(r^2+2 y^2\right)+2 p_2 x y\end{array}\right. {xdistorted =x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ydistorted =y(1+k1r2+k2r4+k3r6)+p1(r2+2y2)+2p2xy
-
将去畸变后的点通过内参数矩阵投影到像素平面,得到该点在图像上的正确位置。
{ u = f x x distorted + c x v = f y y distorted + c y \left\{\begin{matrix}u=f_{x}x_{\text {distorted }}+c_{x} \\v=f_{y} y_{\text {distorted }}+c_{y} \end{matrix}\right. {u=fxxdistorted +cxv=fyydistorted +cy
小结
最后,我们小结一下单目相机的成像过程:
- 首先,世界坐标系下有一个固定的点 P P P,世界坐标为 P w P_{w} Pw。
- 由于相机在运动,它的运动由 R , t R,t R,t或变换矩阵 T ∈ S E ( 3 ) T\in \mathrm{SE} \left ( 3 \right ) T∈SE(3)描述。 P P P的相机坐标为 P ~ c = R P w + t \tilde{P} _{c} =RP_{w} +t P~c=RPw+t。
- 这时的 P ~ c \tilde{P} _{c} P~c的分量为 X , Y , Z X,Y,Z X,Y,Z,把它们投影到归一化平面 Z = 1 Z=1 Z=1上,得到 P P P的归一化坐标: P c = [ X / Z , Y / Z , 1 ] T P_c=[X/Z,Y/Z,1]^T Pc=[X/Z,Y/Z,1]T。
- 有畸变时,根据畸变参数计算 P c P_c Pc去畸变后的坐标 P c ′ P_c^{'} Pc′。
- 最后, P c ′ P_c^{'} Pc′经过内参后,对应到它的像素坐标: P u v = K P c ′ P_{uv}=KP_c^{'} Puv=KPc′。
综上所述,我们一共谈到了四种坐标:世界坐标、相机坐标、归一化坐标和像素坐标。
双目相机模型
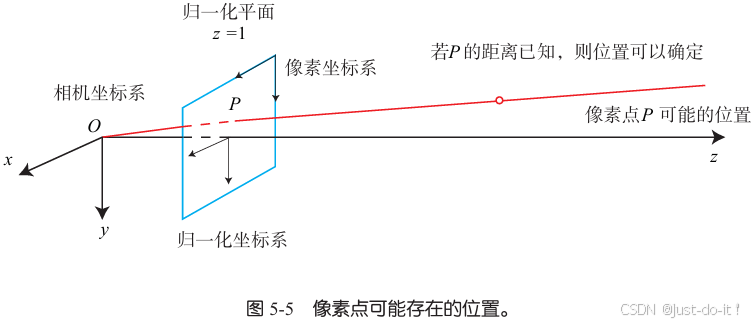
针孔相机模型描述了单个相机的成像模型。然而,仅根据一个像素,我们无法确定这个空间点的具体位置。这是因为,从相机光心到归一化平面连线上的所有点,都可以投影至该像素上。只有当 P P P的深度确定时(比如通过双目或RGB-D相机),我们才能确切地知道它的空间位置。如图5-5所示。
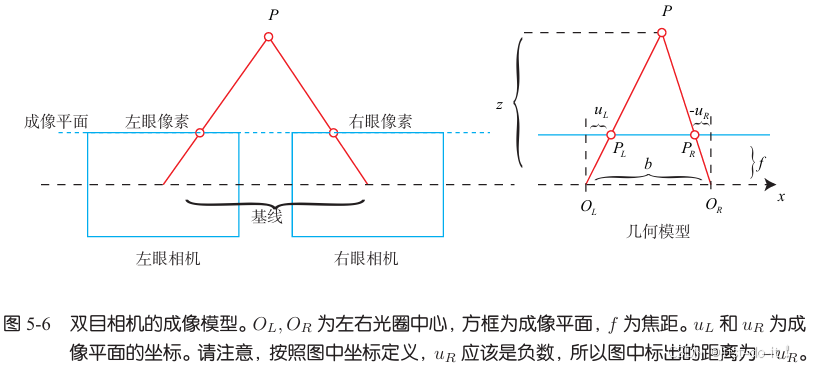
双目相机的原理是通过同步采集左右相机的图像,计算视差来估计每个像素的深度。双目相机通常由水平放置的左眼和右眼相机组成,这两个相机可以被视为针孔相机。由于它们水平放置,两个相机的光圈中心都位于 x x x 轴上。两者之间的距离称为基线(Baseline,记作 b b b),是双目相机的重要参数。
现在,考虑一个空间点 P P P,它在左眼相机和右眼相机各成一像,记作 P L , P R P_{L},P_{R} PL,PR。由于相机基线的存在,这两个成像位置是不同的。理想情况下,由于左右相机只在 x x x轴上有位移,因此 P P P的像也只在 x x x轴(对应图像的 u u u轴)上有差异。记它的左侧坐标为 u L u_L uL,右侧坐标为 u R u_R uR,几何关系如图5-6右侧所示。根据 △ P P L P R \bigtriangleup PP_{L}P_{R} △PPLPR和 △ P O L O R \bigtriangleup PO_{L}O_{R} △POLOR的相似关系,有:
z − f z = b − u L + u R b \frac{z-f}{z}=\frac{b-u_{L}+u_{R}}{b} zz−f=bb−uL+uR
稍加整理,得:
z = f b d , d ≜ u L − u R z=\frac{f b}{d}, \quad d \triangleq u_{L}-u_{R} z=dfb,d≜uL−uR
其中 d d d定义为左右图的横坐标之差,称为视差(Disparity)。
RGB-D 相机模型
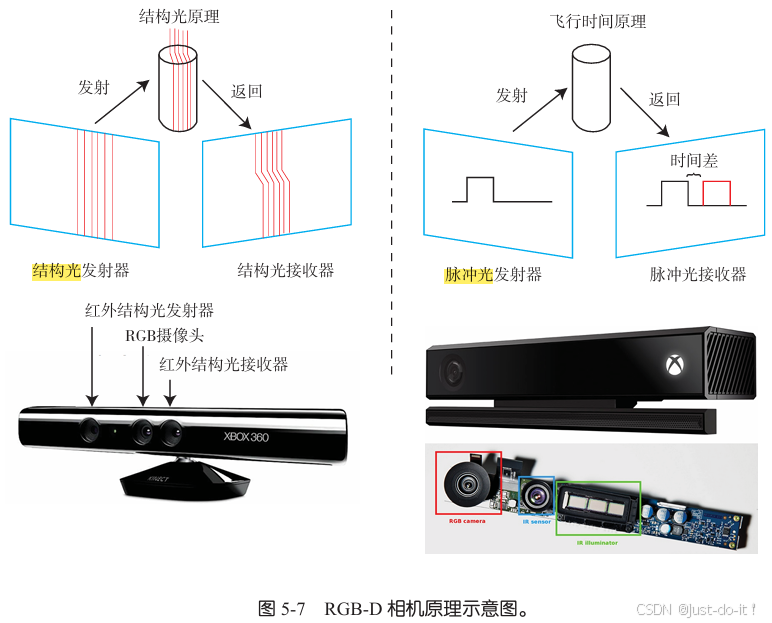
相比于双目相机通过视差计算深度的方式,RGB-D相机的做法更为“主动”一些,它能够主动测量每个像素的深度。目前的RGB-D相机按原理可分为两大类(见图5-7):
- 通过红外结构光(StructuredLight)来测量像素距离的。例子有Kinect1代、ProjectTango1代、Intel RealSense 等。
- 通过飞行时间法(Time-of-flight,ToF)原理测量像素距离的。例子有Kinect2代和一些现有的ToF传感器等。
无论是哪种类型,RGB-D相机都需要向探测目标发射一束光线(通常是红外光)。在结构光原理中,相机根据返回的结构光图案,计算物体与自身之间的距离。而在ToF原理中,相机向目标发射脉冲光,然后根据发送到返回之间的光束飞行时间,确定物体与自身之间的距离。ToF原理和激光传感器十分相似,只不过激光是通过逐点扫描来获取距离,而ToF相机则可以获得整个图像的像素深度,这也正是RGB-D相机的特点。
RGB-D相机能够实时地测量每个像素点的距离。但是,由于这种发射−接收的测量方式,其使用范围比较受限。用红外光进行深度值测量的RGB-D相机,容易受到日光或其他传感器发射的红外光干扰,因此不能在室外使用。在没有调制的情况下,同时使用多个RGB-D相机时也会相互干扰。对于透射材质的物体,因为接收不到反射光,所以无法测量这些点的位置。此外,RGB-D相机在成本、功耗方面,都有一些劣势。