dfs 和 bfs 例题解析

bfs 中利用队列在一次调用中查找许多元素（相当于对数的每一层进行查找）
dfs 中利用递归的形式（实质是栈的性质）在一次调用中继续调用知道输出一种情况后回溯；

bfs

Ac1113.红与黑
搜索和查找

#include<iostream>
#include<cstring>
#define N 25
#include<queue> //用队列实现
using namespace std;

int n,m;
char g[N][N];
int st[N][N];
int res;

int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};

void bfs(int x,int y)
{
    queue<int> q[2]; 
    q[0].push(x),q[1].push(y);
    
    while(!q[0].empty()) //队列不空 
    {
        int t1 = q[0].front(),t2=q[1].front(); //取出队头
        q[0].pop(),q[1].pop();//出队
        
        for(int i=0; i<4; i++) //遍历四个方向
        {
            int a = t1 + dx[i], b = t2 + dy[i]; //队头邻接点的坐标
            
            if(a<0 || a>=n || b<0 || b>=m) continue; //出界
            if(st[a][b] == 1) continue; //已经被访问过
            if(g[a][b] != '.') continue; //不能走
         // if(g[a][b]=='#') continue; // 可能会在加一次@ 因为@这个地方
         								//没有被赋值1；
            res++;
            q[0].push(a),q[1].push(b);
            st[a][b] = 1; //标记(a,b)已经被访问过 
        }
    }
}

int main()
{
    while(cin >>m>>n, m!=0&&n!=0)
    {
        memset(st,0,sizeof(st));//重新初始化
        
        for(int i=0;i<n;i++) cin>>g[i];
        
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            if(g[i][j]=='@')
            {
                res=1; //防止他在多次求值是累加
                bfs(i,j);
                break;
            }
        cout <<res<<endl;
    }
    return 0;
}

bfs 也可应用于找最短路
用bfs算法求最短路径（仅限于权值为一，或者是算出最短步数，一定是第一次搜到的点）

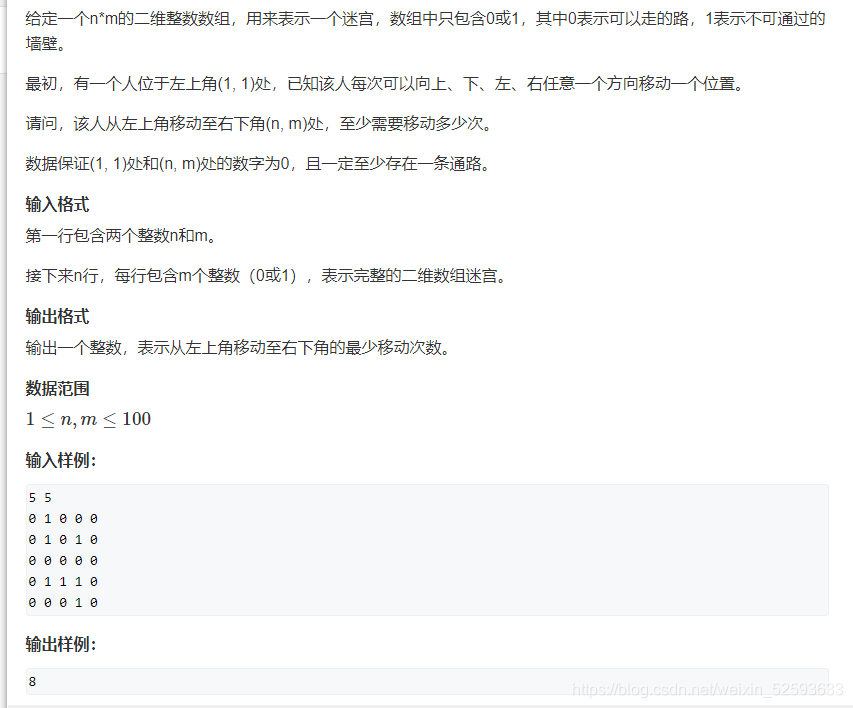
走迷宫
在这里插入图片描述

#include<iostream>
#include<queue>
#define N 105
using namespace std;
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int n,m;
int g[N][N]; 
int dist[N][N];
int bfs(int x,int y)
{
	queue<int>q[2];
	q[0].push(x),q[1].push(y);
	while(!q[0].empty() )
	{
		int t1=q[0].front(),t2=q[1].front() ;
		q[0].pop(),q[1].pop();
		for(int i=0;i<4;i++)
		{
			int a=t1+dx[i],b=t2+dy[i];
			if(a<0||a>=n||b<0||b>=m) continue;
			if(dist[a][b]!=0) continue;
			
			dist[a][b]=dist[t1][t2]+1;
			q[0].push(a),q[1].push(b);
		}
	}
	return dist[n-1][m-1];	//用最先到达的最短距离
}
int main()
{
	cin >>n >>m;
	for(int i=0;i<n;i++)
	for(int j=0;j<m;j++)
		cin >>g[i][j];
	cout <<bfs(0,0);
	return 0;
}

dfs算法

利用递归
红与黑

用C++写一遍思路

#include<iostream>
#include<cstring>
#define N 25
using namespace std;

int n,m;  //n行m列
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int st[N][N];
char g[N][N];

int res;

void dfs(int x,int y)
{
    st[x][y]=1;  //起点也算
    for(int i=0;i<4;i++)
    {
        //朝四个方向出发
        int a=x+dx[i],b=y+dy[i];
        if(a<0||a>=n||b<0||b>=m) continue ;
        if(st[a][b]==1) continue;
        if(g[a][b]=='#')continue;
       // st[a][b]=1;可以统一在递归开始标记；
        res++;
        dfs(a,b);
    }
}
int main()
{
    
    while( cin >>m >>n,m!=0&&n!=0)
    {
     
      // if(m&&n==0)break;
        
        memset(st,0,sizeof(st)); //每一次初始化st[]=0;
        res=1; //起点也算+1
        
        for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            cin >>g[i][j];
            
        for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        if(g[i][j]=='@') 
        {
            dfs(i,j);
            break;
        }
        cout <<res<<endl;
    }
    
    return 0;
}

洛谷 P1443马的遍历（每次要走好几个）

#include<iostream>
#include<queue>
#define N 405
using namespace std;
int n,m;
int x,y;
int g[N][N];
int st[N][N];
int res; 
int dx[8]={-2,-1,1,2,2,1,-1,-2},dy[8]={1,2,2,1,-1,-2,-2,-1};
void bfs(int x,int y)
{
	st[x][y]=-1;
	queue<int>q[2];
	q[0].push(x),q[1].push(y);
	
	while(!q[0].empty())
	{
		int t1 = q[0].front(),t2 =q[1].front();
		q[0].pop(),q[1].pop();
		
		for(int i=0;i<8;i++)
		{
			int a=t1+dx[i],b=t2+dy[i];
			if(a<0||a>=n||b<0||b>=m) continue;
			if(st[a][b]==-1) continue;
			
			st[a][b]=-1; //标记走过 
			g[a][b]=g[t1][t2]+1; //以这个g[t1][t2]为中心往外加1 
			q[0].push(a),q[1].push(b);
		}
	}
	
}
int main()
{
	cin >>n >>m >>x >>y; 
	bfs(x-1,y-1);
	int t = -1;
	for(int i=0;i<n;i++)
	{	
		for(int j=0;j<m;j++)
		{
			if(st[i][j]==-1) printf("%-5d",g[i][j]);
			else printf("%-5d",t);
		}
		cout <<endl;
	}
	return 0;
}

dfs深度搜索
AC 细胞数量（查完所有同一细胞）

#include<iostream>
#define N 105
using namespace std;

int n,m;  //n行m列
char g[N][N];

int res;
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};

void dfs(int x,int y)
{
    for(int i=0;i<4;i++)
    {
        //朝四个方向出发
        int a=x+dx[i],b=y+dy[i];
        if(a<0||a>=n||b<0||b>=m) continue ;
        if(g[a][b]=='0') continue; //如果没有这个就一直递归啦；
        
        g[a][b]='0';
        dfs(a,b);
    }
}
int main()
{
    cin >>n>>m;
    for(int i=0;i<n;i++)
       for(int j=0;j<m;j++)
            cin >>g[i][j];
	for(int i=0;i<n;i++)
      for(int j=0;j<m;j++)
        if(g[i][j]!='0') 
        {
        	res++;
            dfs(i,j);
        }
        cout <<res;
    
    return 0;
}

p1219 八皇后问题

一个如下的 6×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

在这里插入图片描述

上面的布局可以用序列 2\ 4\ 6\ 1\ 3\ 5 来描述，第 ii 个数字表示在第 ii 行的相应位置有一个棋子，如下：

行号 1\ 2\ 3\ 4\ 5\ 6

列号 2\ 4\ 6\ 1\ 3\ 5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。

输入格式
一行一个正整数 n，表示棋盘是 n×n 大小的。

输出格式
前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入
6
输出
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

#include<iostream>

using namespace std;
const int N=100;

int n;
int cnt;
int a[N],b[N],c[N],d[N];

//a[]是行 b[]是列 
//c[]是左下到右上 d[]是左上到右下  

void out()
{
	if(cnt<=3)
	{
		for(int i=1;i<=n;i++)
		{
			cout <<a[i]<<' ';
		}
		cout <<endl;
	}
	cnt ++;
}

void dfs(int i) //传过来的数据是行 
{
	if(i>n)
	{
		out();
		return ;
	}
	
	for(int j=1;j<=n;j++) //循环是从第一列开始 x 和 i比较 
	{
	   //  c[2+3]等于c[3+2] 左下到右上  d[1-1+n]等于d[n-n+n] 左上到右下 
		if((!b[j])&&(!c[i+j])&&(!d[i-j+n]))//如果没有皇后占领，执行以下程序
            {
                a[i]=j;//标记i排是第j个 把这个j列填入a[]空里面 
                b[j]=1;
                
                c[i+j]=1;
                d[i-j+n]=1;
                //占领两条对角线及平行线 
                dfs(i+1);//进一步搜索，下一个皇后
                b[j]=0;
                c[i+j]=0;
                d[i-j+n]=0;
                //（回到上一步）清除标记
            }
	}
	return  ; //返回上一步 
}
int main()
{
	cin >>n;
	dfs(1);
	cout <<cnt;
	return 0;
 }

dfs 和 bfs 例题解析

bfs

dfs算法

悦读