友友们好(^-^)🌹🌹🌹,我是杨枝,一枚在算法领域迈步的呆萌的博主呀~
目前还是一只纯纯的菜汪🐶。 典型的又菜又爱闹那种👀,做不好很多事,说不好很多话,写题还总不Ac😅,还在努力还在前进👣。
因为了,你们对我来说都是是独一无二的呀💓。在点开这篇文章的那一刻,我相信,我们之间相互需要彼此啦🌹🌹
时刻谨记:认真写算法,用心去分享。不负算法,不误卿。 感谢相遇(^㉨^)。
蓝桥杯的十种呼吸法是笔者结合自己的学习筛选出来的十个知识点。本着像看漫画一样了解算法原理。当日后自己确实遇到相关的习题了,可以再回头结合着我的题解报告来加深理解喔。
🔔八仙过海,智斗二分
小伙伴们对忍姐姐那把独特的日轮刀有没有印象了,感觉喃,舞起来好轻巧,看着好潇洒
但是忍姐姐的结局好容易爆泪点呀😭😭无限城中就这种牺牲了😭😭😭
害,得回归正题啦~
到蝴蝶屋中开始修习咱们今天要学的呼吸之法 —— 二分啦
💓据说只有10%的程序员可以写对二分
二分的基础用法是在单调序列或单调函数中进行查找。因此当问题具有单调性的时候,就一定可以通过二分把求解转换为判定。说通俗一点了,可理解为判断出答案在这个单调区间的位置
(根据复杂度理论,进行判定的难度小于进行求解)。
| 进一步,我们还可以扩展到通过三分法解决单峰函数的极值以及相关的问题。 |
| 二分难点在于对细节的处理: |
对于整数域上的二分,需要注意终止边界、左右区间取舍时的开闭情况,避免漏掉答案或造成死循环;
对于实数域的二分,需要注意精度问题。
🌟整数集合上的二分
使用二分法的前提是保证最终答案处于闭区间 [ l , r ] [l,r] [l,r]之内,循环以 l = r l = r l=r结束,每次二分的中间值 m i d mid mid会归属于左半段与右半段二者之一。
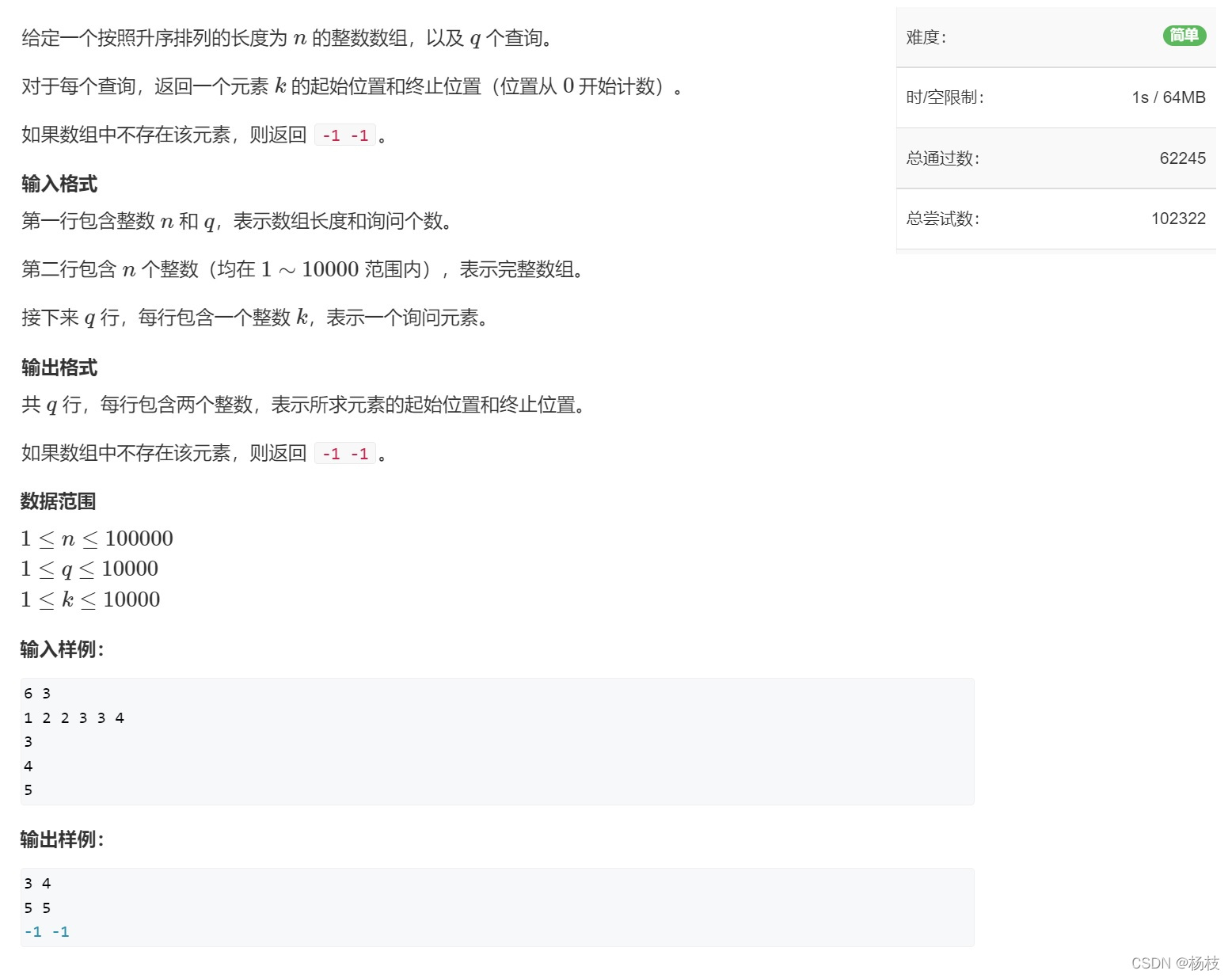
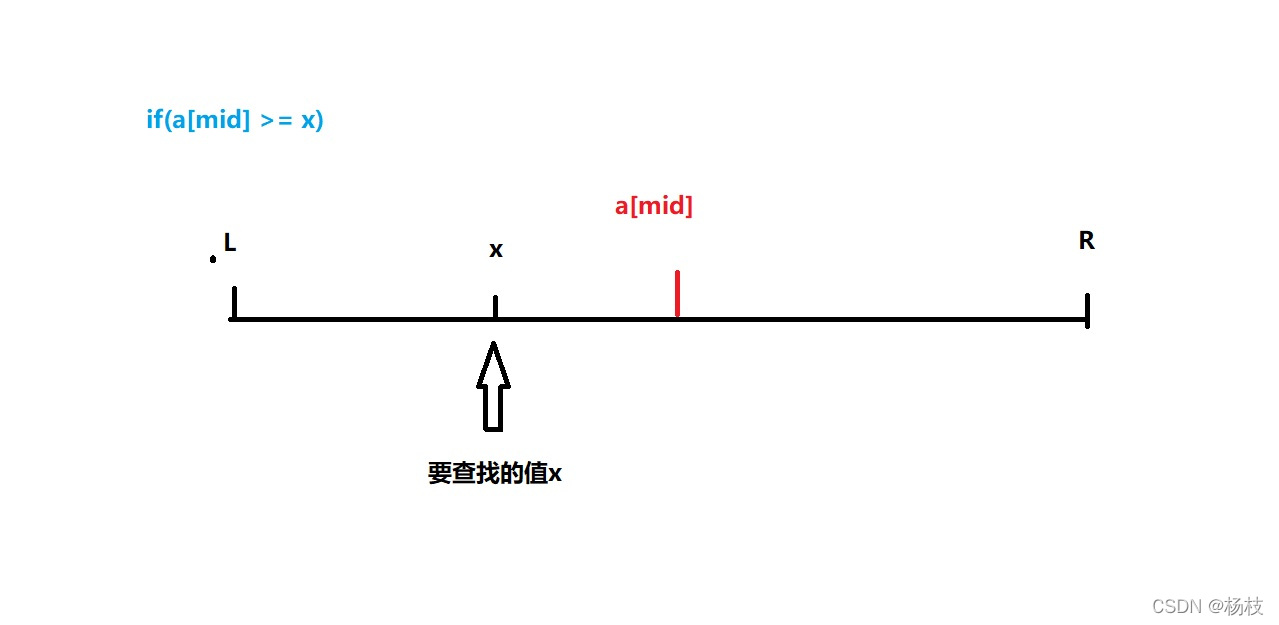
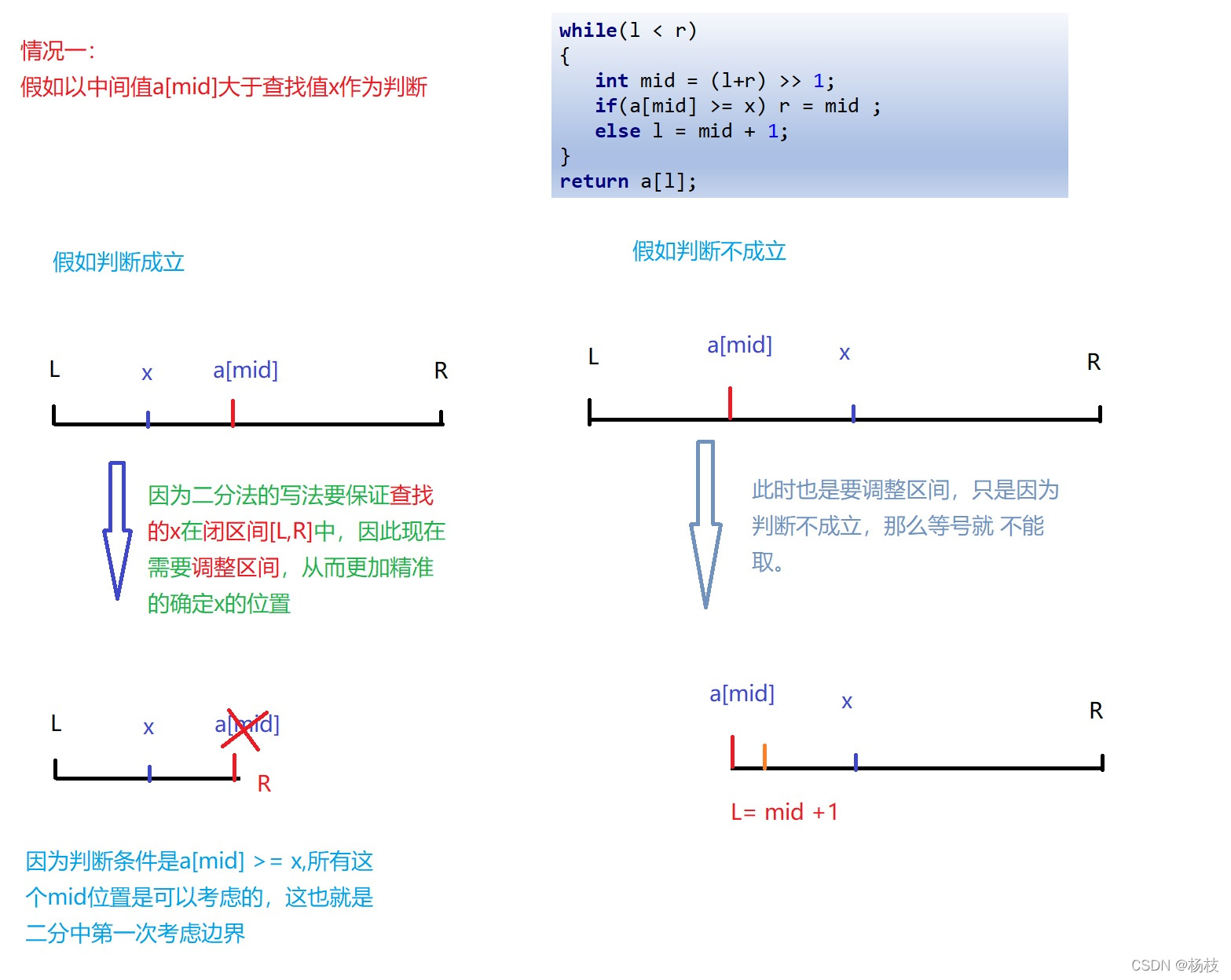
情况一:在单调递增序列 a a a中查找大于等于x的数最小的一个位置。
while(l < r)
{
int mid = (l+r) >> 1;
if(a[mid] >= x) r = mid ;
else l = mid + 1;
}
return a[l];
情况一用图片演示的效果如下:
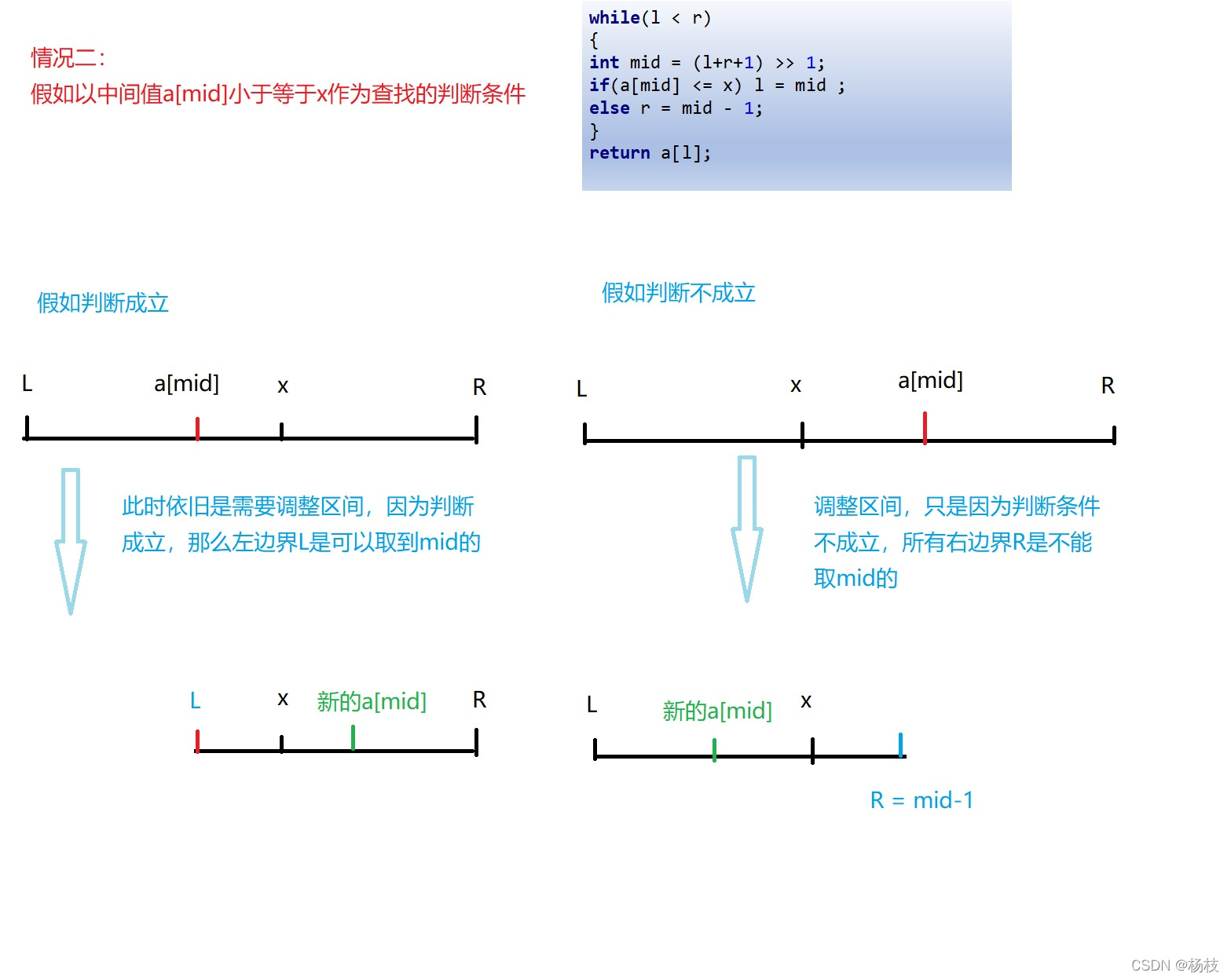
情况二:在单调递增序列a中查找小于等于x的数中最大的一个位置
while(l < r)
{
int mid = (l+r+1) >> 1;
if(a[mid] <= x) l = mid ;
else r = mid - 1;
}
return a[l];
对于情况二用图片演示效果如下:
| 如同上面两段代码所示,这种二分写法可能会有两种形式: |
1、范围缩小时, r = m i d r=mid r=mid, l = m i d + 1 l=mid+1 l=mid+1,取中间值时, m i d = ( l + r ) > > 1 mid = (l+r)>>1 mid=(l+r)>>1
2、范围缩小时, l = m i d l=mid l=mid, r = m i d − 1 r=mid-1 r=mid−1,取中间值时, m i d = ( l + r + 1 ) > > 1 mid = (l+r+1)>>1 mid=(l+r+1)>>1
注意第二段的写法,倘若第二段也是采用 m i d = ( l + r ) > > 1 mid = (l+r)>>1 mid=(l+r)>>1,那么当 r − l = 1 r-l=1 r−l=1时,即 r = l + 1 r = l+1 r=l+1,那么就会出现:
m i d = ( r + l ) > > 1 mid = (r+l)>>1 mid=(r+l)>>1 = ( l + 1 + l ) > > 1 (l+1+l)>>1 (l+1+l)>>1 = l l l。
若接下来进入 l = m i d l=mid l=mid的分支,可行的区间并没有缩小,会造成死循环。
若进入 r = m i d − 1 r = mid-1 r=mid−1的分支,会造成 l > r l>r l>r,循环结束。
因此,对两个形式采用的配套的
m
i
d
mid
mid 取法是必要也必须遵守的。
注意我们在二分中使用的是
右移运算:
>
>
1
>>1
>>1,而不是整数除法
/
2
/2
/2。两者大体是差不多的,只是有细微的区别。
| 右移运算是向下取整,而整数除法是向零取整,在二分值域包含负数时,整数除法是不能正常工作的。 |
🌟实数域上的二分
在实数域上的二分较为简单,确定好所需的精度 e p s eps eps
以 l + e p s < r l+eps<r l+eps<r 为循环条件,每次根据在 m i d mid mid 上的判断的成立与否,选择 r = m i d r=mid r=mid 或者是 l = m i d l=mid l=mid。一般需要保留 k k k 位小数的时候,则取 e p s = 1 0 − ( k + 2 ) eps = 10^{-(k+2)} eps=10−(k+2)
//倘若题目要求保留三位小数
while(l + 1e-5 < r)
{
double mid = (l+r) / 2;//在算法题里,建议多用double,float有时候会因为精度问题导致结果有细微偏差
if(判断条件) r = mid;
else l = mid;
}
有时候精度不容易确定或者表示,就干脆可以采用循环固定次数的二分方法,也是一种相当不错的策略,这种方式得到的结果的精度往往比设置
e
p
s
eps
eps 的更高。
for(int i = 0; i < 100;i++)
{
double mid = (l+r) /2;
if(判断条件) r = mid;
else l = mid;
}
小伙伴们现在应该有种模糊的感觉, g e t get get二分法的 精髓了,咱们着手看一点习题,切实的体会一下怎么把二分这套功法打出去吧
💓趁热打铁,开始练习
🌟例1、数的范围
🌱题目描述
🌴解题报告
| 题目想要咱们确定查找的数字的起始位置。想实现这个,就需要对二分的两种情况再理解。 |
对于情况一,在 i f ( a [ m i d ] > = x ) if(a[mid] >= x) if(a[mid]>=x)的条件下成立,那么这个查找值 x x x是在中点的左边,那就可以理解为确定当前区间的左边界
同理,对情况二进行同样的理解,情况二就可以理解为确定右边界。
那么解决这道题就很轻松啦,依次将两种情况使用上就好,注意不要将顺序弄反喔~
🌵参考代码(C++版本)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010 ;
int q[N];
int n,m;
int main()
{
scanf("%d %d",&n,&m);
//录入n个信息
for(int i= 0; i < n;i++) scanf("%d",&q[i]);
//m个询问
for(int i = 0; i < m;i++)
{
int x;
scanf("%d",&x);
//通过作图+理论分析,其实还是不恼火的
//先确定左端点
int l = 0, r = n-1;
while(l < r)
{
int mid = l + r >> 1;
//把这个二分出来的mid和x做比较
if(q[mid] >= x) r = mid;
else l = mid +1;
}
if(q[l] == x)
{
cout << l <<' ';
r = n-1;
//确定右端点
while(l < r)
{
int mid = l+r+1 >> 1;//这里按照之前的理解来分析的话,直接就裸写 l+r >> 1。再通过后面代码分析要不要补上1
if(q[mid] <= x) l = mid;
else r = mid -1;
}
cout << r <<endl;
}else cout << "-1 -1" << endl;
}
return 0;
}
成功斩杀第一个小怪兽~,进攻下一个
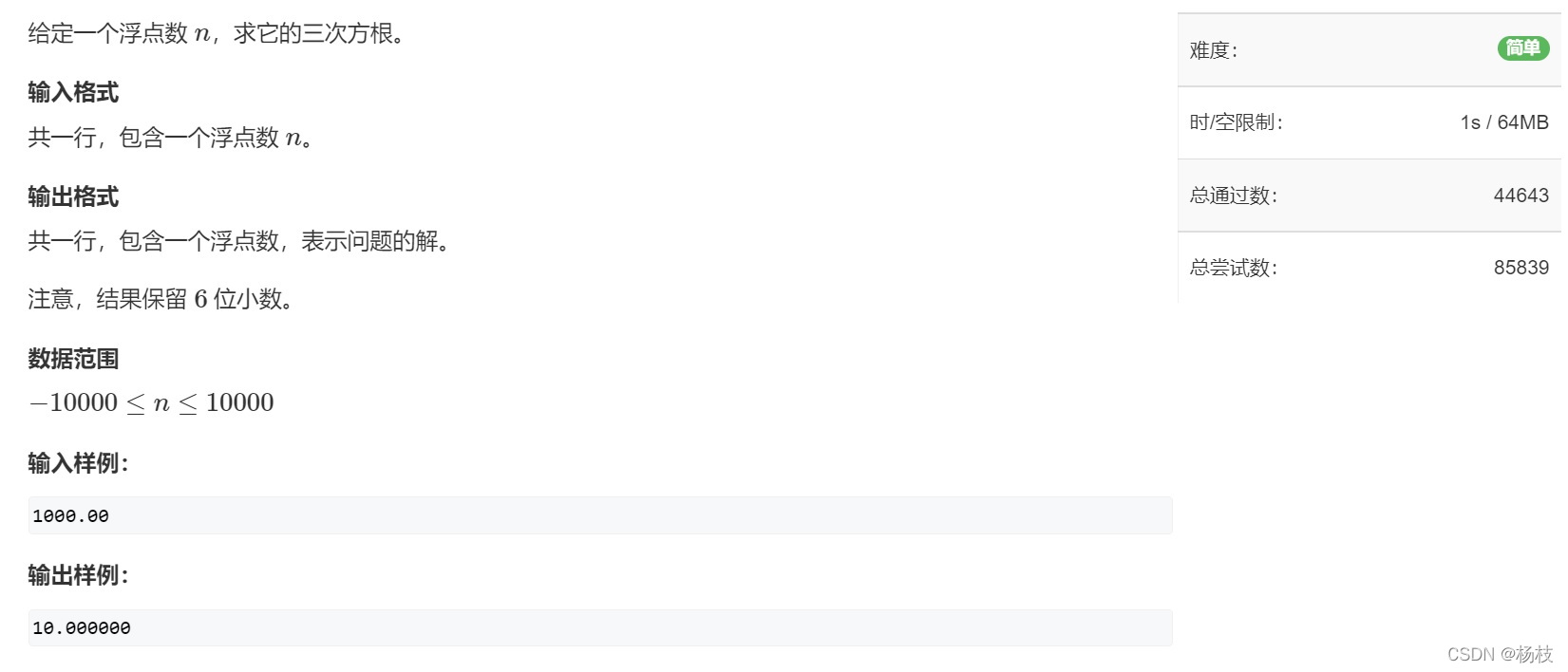
🌟例2、数的三次方根
🌱题目描述
🌴解题报告
题目给咱的的是一个浮点数,也就是属于实数域的二分。那咱们只需要指定一个判断条件,然后持续二分到精度 s p s sps sps = 10-8的程度再停止。
因为让我们求一个数的三次方根是多少,那么判断条件就可以定为:
i
f
(
m
i
d
∗
m
i
d
∗
m
i
d
>
=
x
)
if(mid * mid * mid >= x)
if(mid∗mid∗mid>=x)
🌵参考代码(C++版本)
#include <cstdio>
int main()
{
double x;
scanf("%lf",&x);
double l = -10000,r =10000;
while(r-l >= 1e-8)
{
double mid = (l+r) / 2;
if(mid*mid*mid >= x) r =mid;
else l = mid;
}
printf("%.6lf",l);
return 0;
}
完美解决
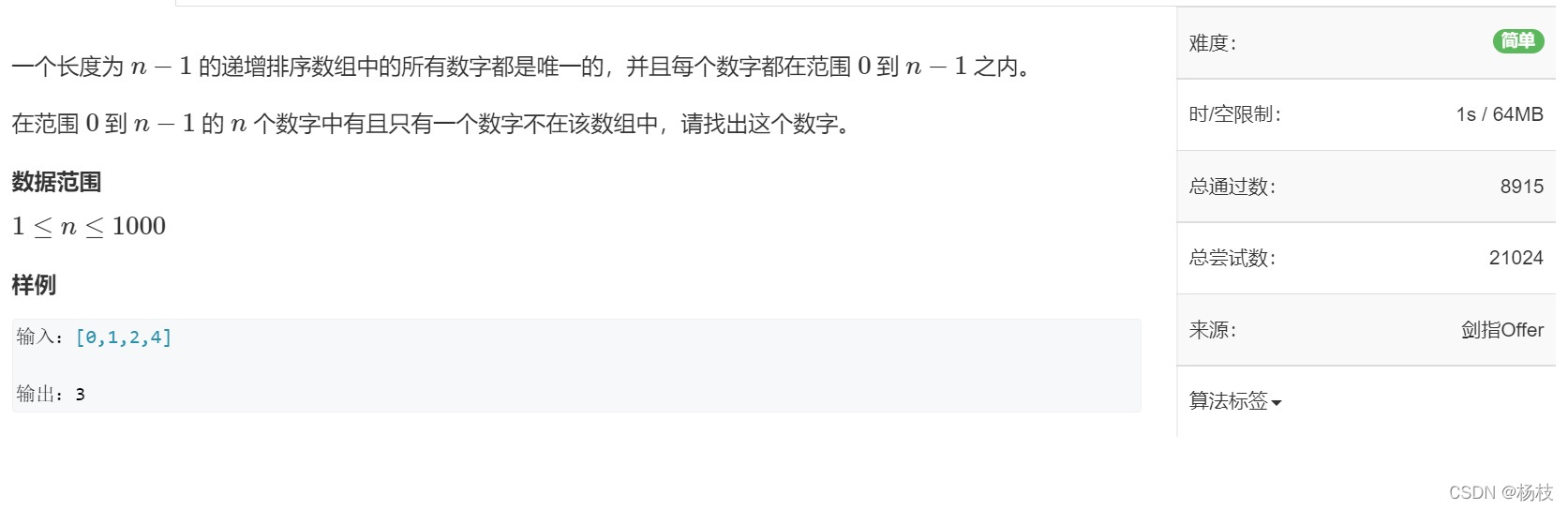
🌟例3、0到n-1中缺失的数字
🌱题目描述
🌴解题报告
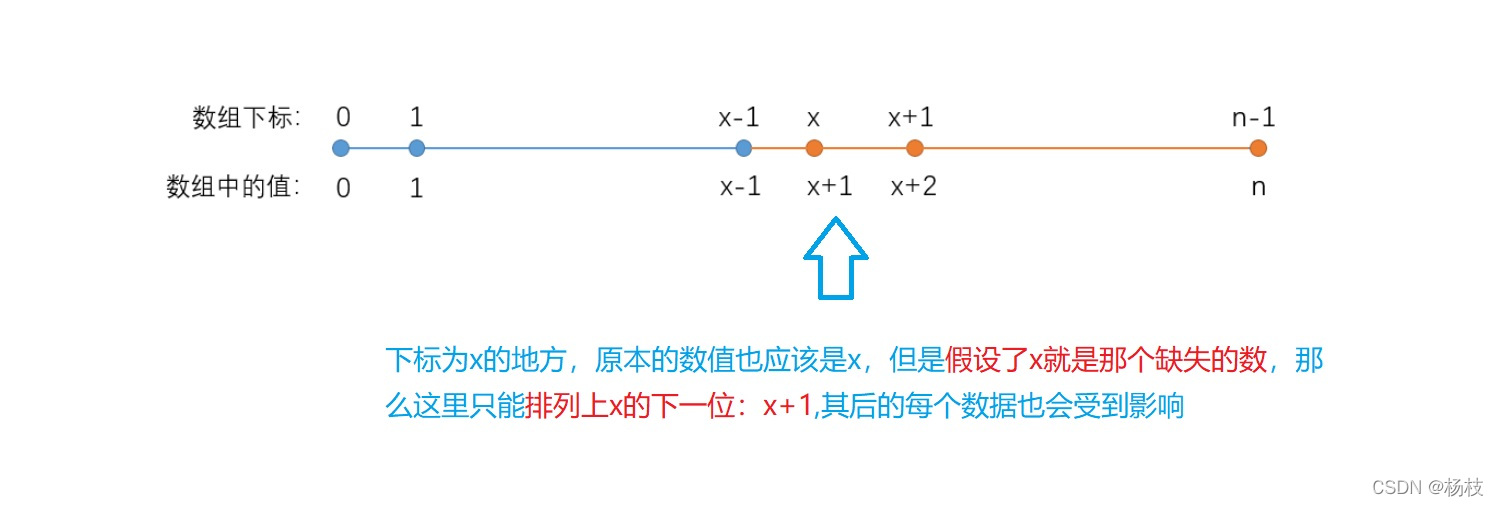
这道题目给定的是递增数组,假设数组中第一个缺失的数是
x
x
x。
那么数组中下标和该下标存储的数的实际情况如下:
可以观察到:
可以看出,数组左边蓝色部分都满足nums[i] == i;
数组右边橙色部分都不满足nums[i] == i。
因此我们可以将是否满足nums[i] == i作为确定二分的分界点
x
x
x 的判断条件
另外要注意特殊情况:当所有数都满足nums[i] == i时,表示缺失的是
n
n
n
至于时间复杂度:
二分的迭代只会执行
O
(
l
o
g
n
)
O(logn)
O(logn) 次,那么时间复杂度
O
(
l
o
g
n
)
O(logn)
O(logn)。在时间上,完全没有问题。
🌵参考代码(C++版本)
class Solution {
public:
int getMissingNumber(vector<int>& nums) {
if(nums.empty()) return 0;
//二分查找
int l = 0 , r = nums.size()-1;
while(l < r)
{
int mid = (l+r) >> 1;
//如果二分出来的所有中点值mid,不等于对应的数据值,就继续二分查找
if(nums[mid] != mid) r = mid;
else l = mid+1;
}
//返回结果
if(nums[r] == r ) r++;
return r;
}
};
快乐Ac
🌟例4、试题 算法训练 找数2
🌱题目描述
🌴解题报告
读完题目之后,能了解到这道题是想让我们查找一个数的位置:
倘若在一串数据中查找到这个数字了,那么输出位置(注意位置是从1开始数的); 倘若没有查到这个数字,确定这个输入数据应该插入的位置。
对于查找的需求,可以使用二分来高效完成。
使用情况一和情况二都可以,注意边界。
| 对于确定插入的位置,我的思路比较暴力,是直接逐一枚举同时比较出与输入数据相差最小的数。当找到以后,这个差值最小且差值大于零的数,它后面一位就是合适的位置。 |
结合着样例,具体落实一下我刚才说的话吧,只听描述很空洞的,笔者我自己也不喜欢很空洞的东西。
样例输入
10
23 34 56 78 99 123 143 155 167 178
128
样例输出
7
比如这个样例,输入数据128和123之间的差值为5,是差值最小的正整数。123的位置是6,它后面一位就是7。
🌵参考代码(C++版本)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1010;
int q[N];
int n,mid;
int main()
{
int x;
int ans = 0x3f3f3f3f;
int pos = 0;
scanf("%d",&n);
//录入数据
for(int i =0; i < n;i++) scanf("%d",&q[i]);
scanf("%d",&x);
//开始二分
int l = 0, r = n-1;
while(l < r)
{
mid = (l + r) >> 1;
if(x <= q[mid]) r = mid;
else l = mid +1;
}
//二分到了,输出位置
if(x == q[l]) printf("%d",l+1);
else //没有二分到要查找的数,把插入进去
{
for(int i = 0; i < n;i++)
{
//一个小优化同时也是处理比最后一个数据还大的情况
if(x > q[n-1])
{
pos = n;
break;
}else
if(ans > 0 && x- q[i] < ans)
{
ans = x-q[i];
pos = i;//记录位置
}
}
//输出位置
printf("%d",pos+1);
}
return 0;
}
从上面几个小例题中,应该逐渐体会到了,二分在查找领域里面是占了一席天地的。因为它的时间复杂度是 O ( l o g n ) O(logn) O(logn)。
就比如上海到杭州的某处电话线断了,其间有30万根电线杆,逐一枚举的话,就是30万次。
使用二分法去查找的话,大概只需用20次的样子。效率相当可观。
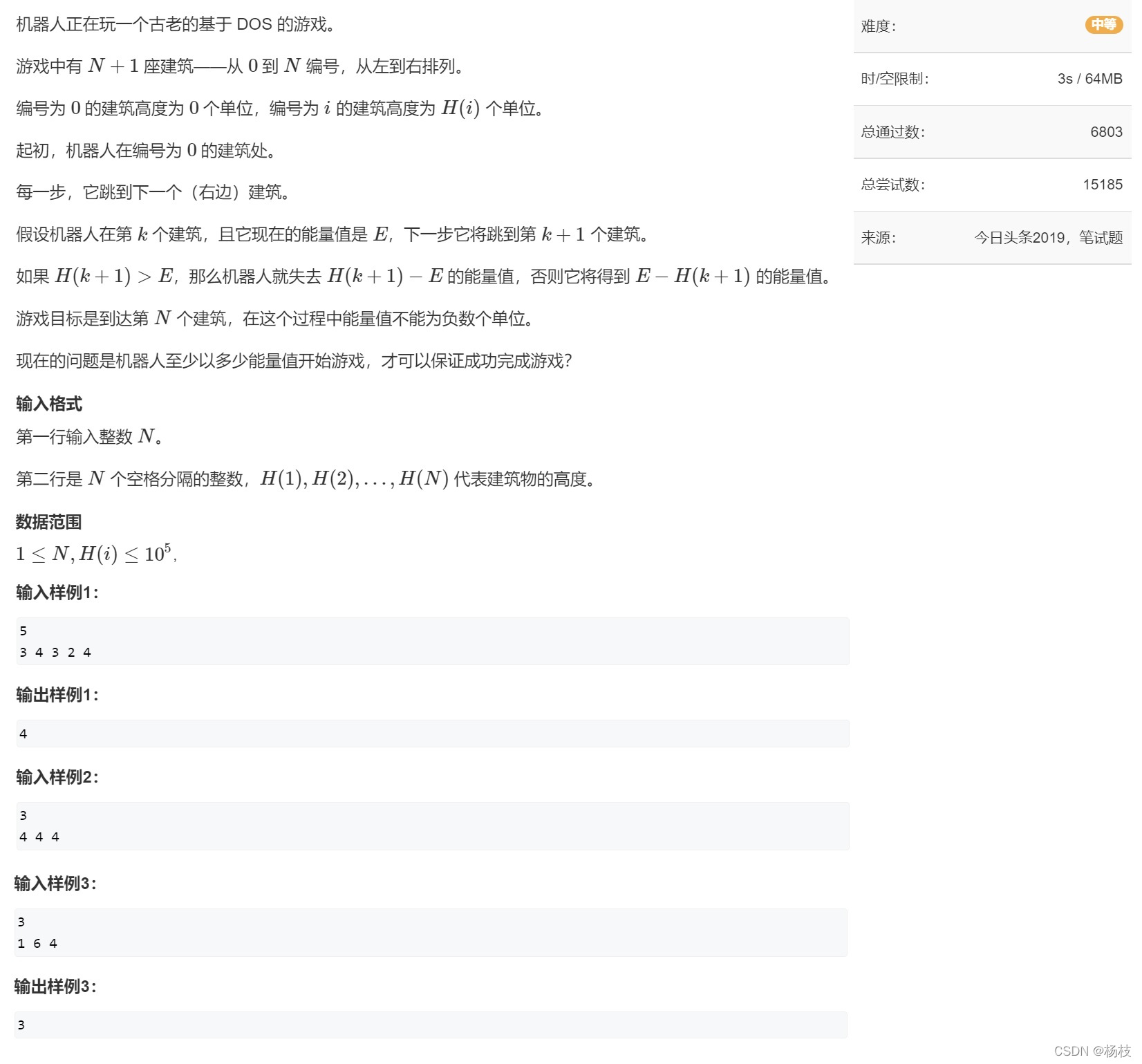
🌟例5、今日头条2019 机器人跳跃问题
🌱题目描述
🌴解题报告
一、从数据范围定算法
题目的数据范围是1到十万,根据我在水之呼吸.壹之型.递归中罗列出的表单,是可以选择二分的。比起其他算法,二分实现相对更容易,那咱们就按照二分的思路解了。
题目在输出格式中说明了要输出整数,那么这道题是隶属于整数二分
二、题目分析
题目中机器人能量消耗可以粗糙的理解为:
向上跳跃可以消耗能量就需要进行做减法;至于向下跳跃可以获得能量就需要进行做加法。
那么,
如果
H
(
k
+
1
)
>
E
H(k+1) > E
H(k+1)>E,则:
E
=
E
−
(
H
(
k
+
1
)
−
E
)
E = E-(H(k+1)-E)
E=E−(H(k+1)−E) =
2
∗
E
−
H
(
k
+
1
)
2*E-H(k+1)
2∗E−H(k+1)
如果
H
(
k
+
1
)
<
E
H(k+1) < E
H(k+1)<E,则:
E
=
E
+
E
−
H
(
k
+
1
)
E = E+E-H(k+1)
E=E+E−H(k+1) =
2
∗
E
−
H
(
k
+
1
)
2*E-H(k+1)
2∗E−H(k+1)
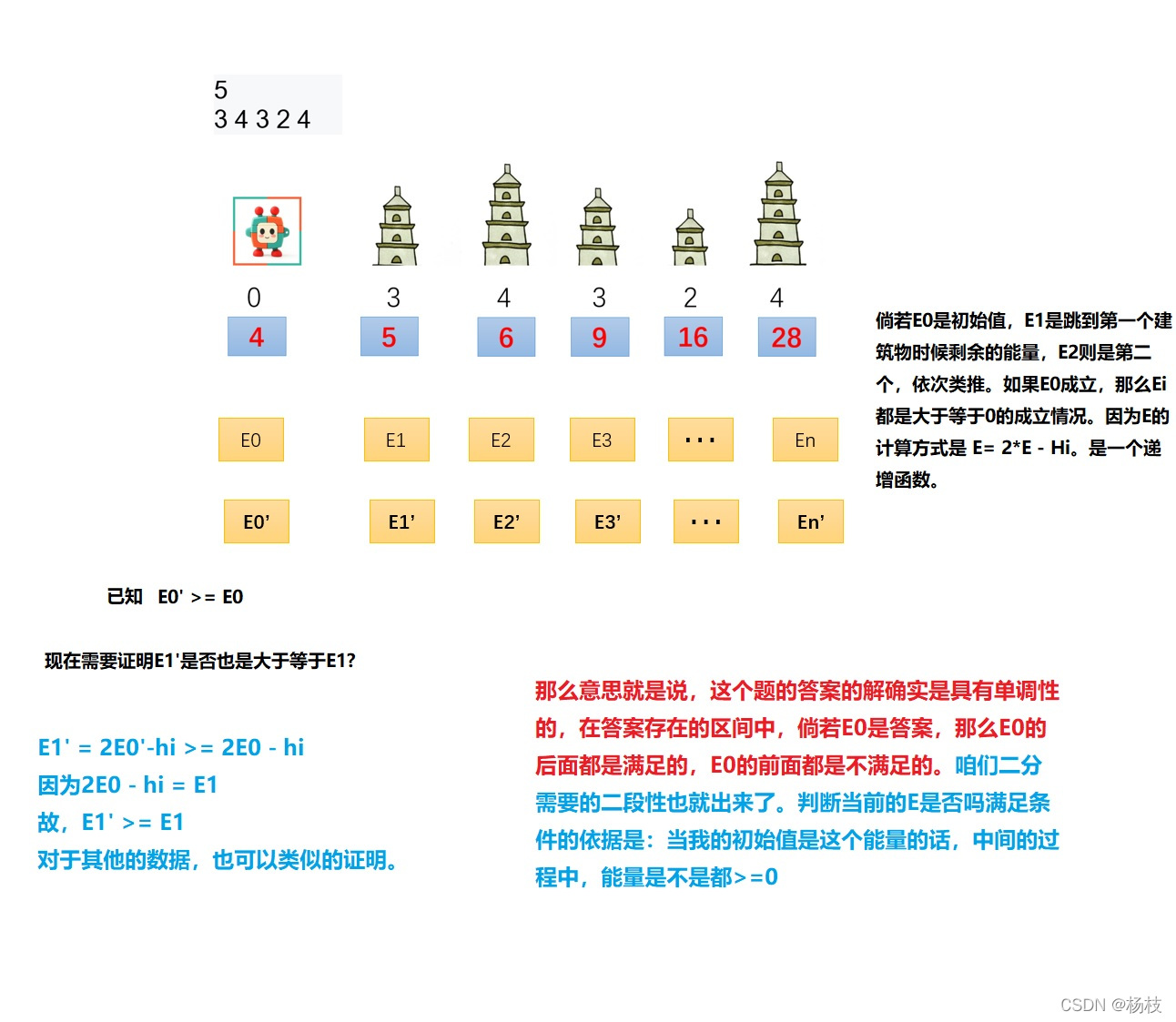
通过对题目中能量变化的分析,总结出无论向更高的建筑跳跃,还是向更低的塔跳跃,能量的变化的计算方式都是相同的。
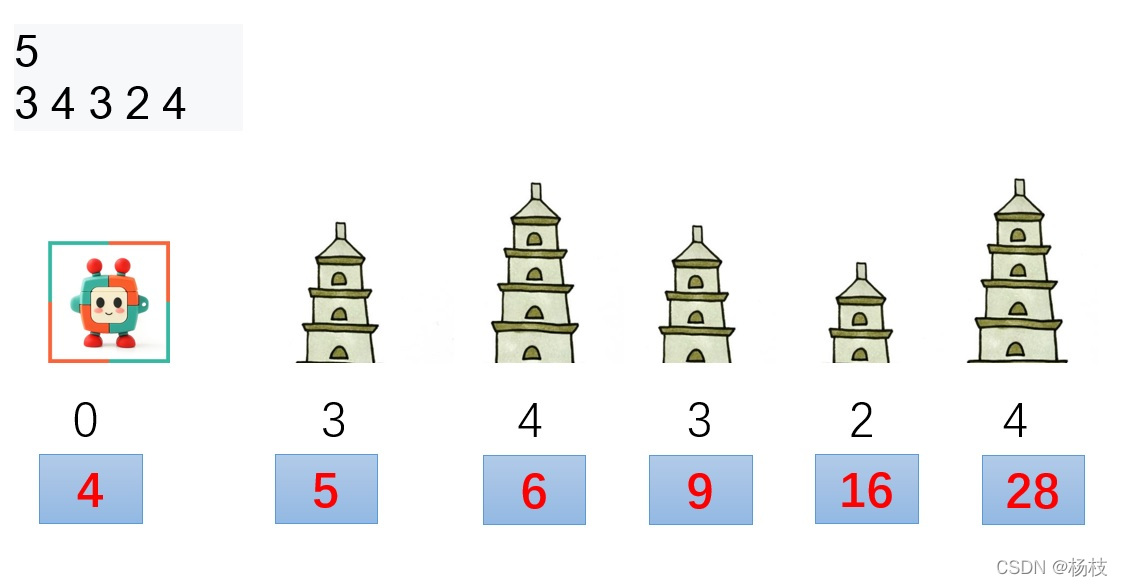
咱们依着这个公式来模拟一下题目的样例。
可以看到整个环节是不会出现中题目中规定的能量为负的情况,故初始能量可以是4。
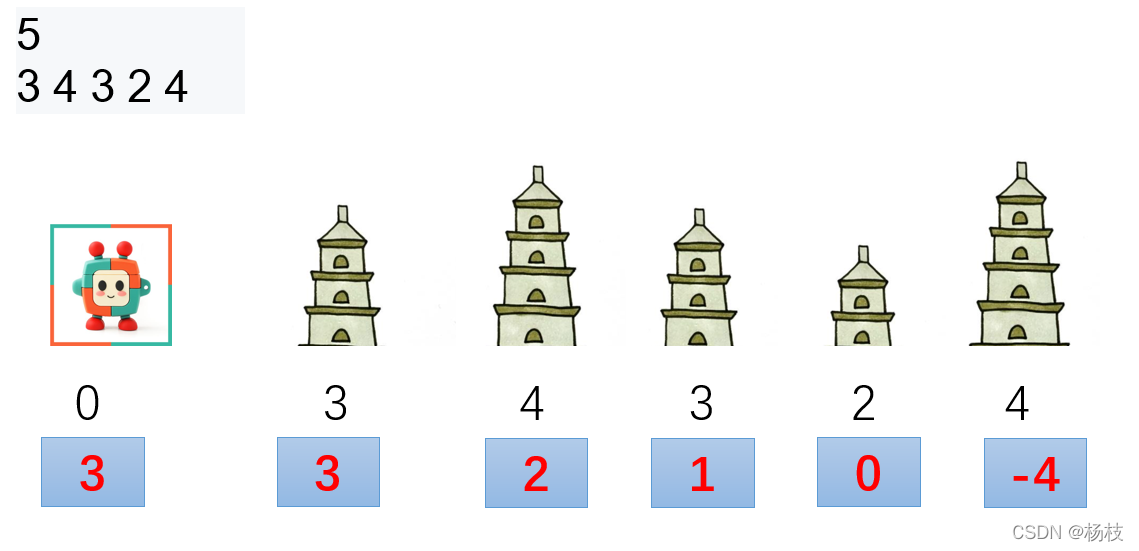
倘若是初始能量为3,那么就会出现能量为负的情况
三、确定性质
性质。找到单调性,有单调性一定能够使用二分。或者找到具有二段性的性质,这个性质可以使得部分数据不满足,但部分数据满足。
倘若初始值 E 0 E_0 E0满足要求,现在存在 E 0 ′ E'_0 E0′ >=
E 0 E_0 E0,假如 E 0 ′ E'_0 E0′也可以满足要求,那么就是具有单调性的。因此 E 0 E_0 E0就应该是这个最小的值,咱们就可以把它二分出来了。
拓展:此题单调性的证明(感兴趣的小伙伴可以)
四、确定二分的形式
是选择情况一还是情况二了?即,究竟是 r = m i d r = mid r=mid还是 l = m i d l = mid l=mid了
如果用于判断的函数叫做
c
h
e
c
k
(
)
check()
check()。
倘若
c
h
e
c
k
(
m
i
d
)
check(mid)
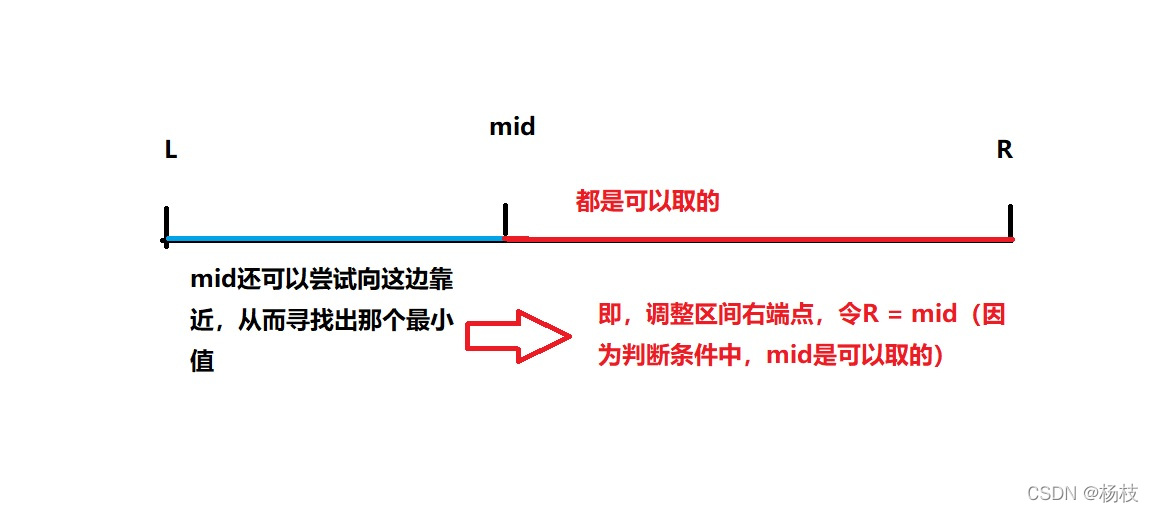
check(mid)成立,意思
m
i
d
mid
mid是可以取的。那么
m
i
d
mid
mid的右边都是可以取的,为了更精准的确定到查找的数据,应该调整右区间,即
r
=
m
i
d
r=mid
r=mid。
五、
c
h
e
c
k
check
check函数的实现
把传入的数据递推一下,判断期间有没有0。出现了0,那么当前这个方案就是不合适的。
🌵参考代码(C++版本)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int h[N];
bool check(int e)
{
//递推枚举
for(int i = 1; i <= n;i++)
{
e = e*2 -h[i];
//(e >= 1e5)应对的情况是当某一时刻算出来的e已经大于最大高度maxh了,那么这个e后面的数据
//也一定是符合要求的,可以直接return ture;以此实现优化,防止中间过程爆int
if(e >= 1e5) return true;
if(e < 0) return false;//出现0,返回false
}
return true;
}
int main()
{
scanf("%d",&n);
for(int i = 1;i <= n;i++) scanf("%d",&h[i]);
//确定边界
int l = 0, r = 1e5;
while(l <r)
{
int mid = l+r >>1;
if(check(mid)) r = mid;
else l = mid+1;
}
//输出答案
printf("%d",l);
return 0;
}
🌟例6、第七届蓝桥杯省赛C++A/B组 四平方和
🌱题目描述
🌴解题报告(两个建议掌握的小技巧)
一、依靠数据范围确定枚举个数
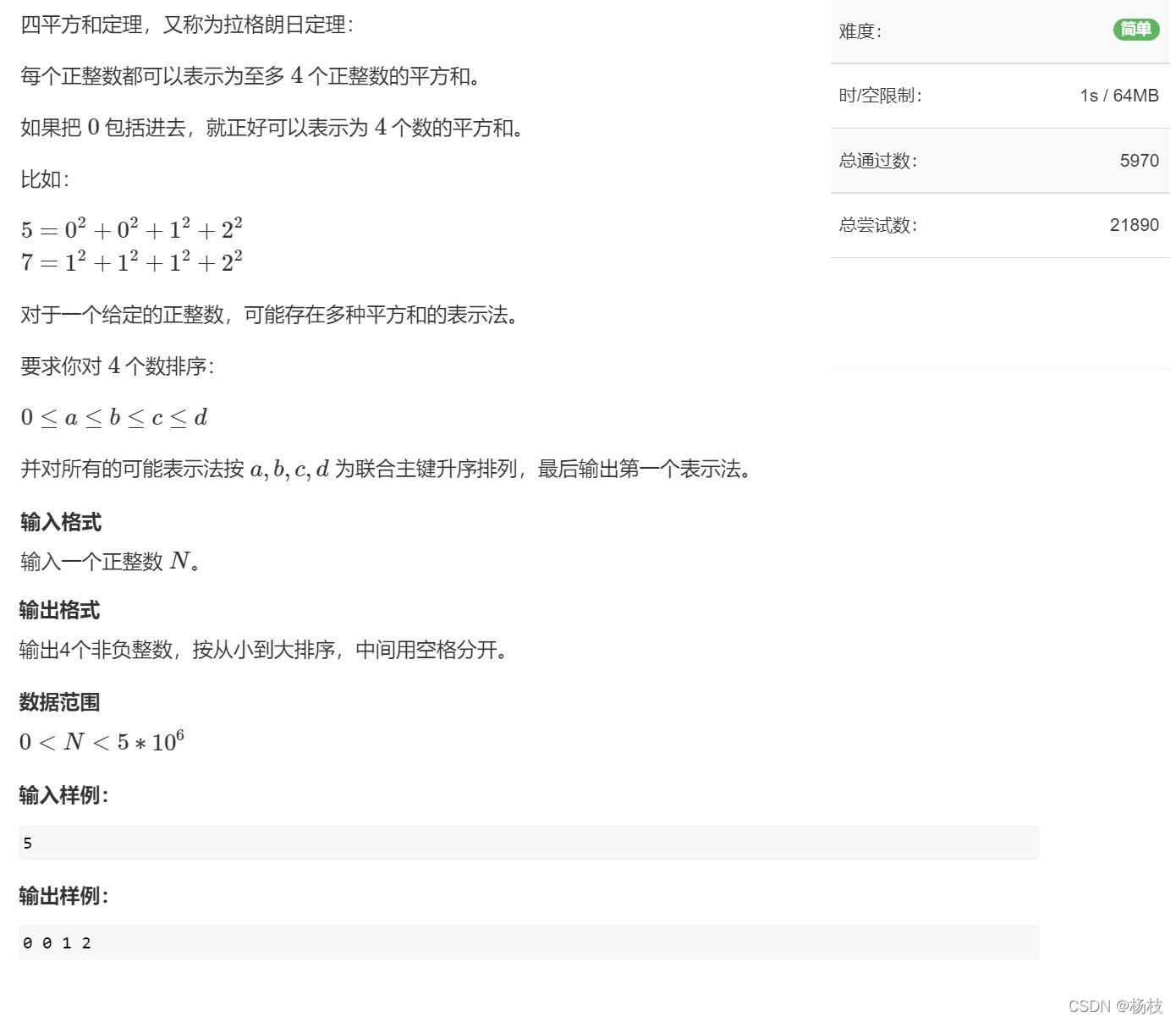
题目中说:每个正整数都可以表示为至多
4
4
4个正整数的平方和。
给咱的数据范围是0 <
N
N
N <
5
∗
1
0
6
5∗10^6
5∗106。
那么对于每个数
a
、
b
、
c
、
d
a、b、c、d
a、b、c、d而言,可以取的范围应该都是0 ~
N
\sqrt N
N,大于是2000到3000之间嘛。掏出可以的计算器可以更具体的计算出大约是2236。
这里就可以使用一个通过数据范围确定最多可以枚举的数的个数的技巧。
倘若直接暴力枚举的话,应该需要枚举3个数: a 、 b 、 c a、b、c a、b、c
那么时间复杂度就是
233
6
3
2336^3
23363,就算去点零头,看做
200
0
3
2000^3
20003,也会进行
8
∗
1
0
9
8*10^9
8∗109次运算,直接超过了C++一秒能进行的一亿次运算。所有我们最多只能枚举两个数。
二、空间换时间
空间换时间是算法题中经常会用到的思想,建议拿捏上。算法题中时间更为重要。
具体的方式是先枚举两个数,比如枚举
c
和
d
c和d
c和d。将它们的计算结果
c
2
+
d
2
c^2+d^2
c2+d2存储起来。再去枚举
a
和
b
a和b
a和b,此时就只用到存储的数据中,查找合适的数据就可了。
三、查找方式
| 提到查找方式,最容易想到的应该是哈希和二分。我这里就重点落实二分的代码吧,哈希的代码我放在gitee中,友友们可以自行采摘。 |
四、重载小于符号
因为存下
c
2
+
d
2
c^2+d^2
c2+d2的总和以后,待会要用于求
a
2
+
b
2
a^2+b^2
a2+b2的环节中去从小到大的查找。因此要对存储的数据进行排序,那么就需要重新对小于符号的比较方式进行规定。
🌵参考代码(C++版本)
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5e6+10;
//开一个结构体用来存储c^2+d^2的信息吧
struct Sum{
int s,c,d;
//因为待会需要对c^2+d^2的信息进行sort排序,需要重新定义小于符号
bool operator <(const Sum &tmp) const
{
if(s != tmp.s) return s < tmp.s;//先按总和从小到大排序
if(c != tmp.c) return c < tmp.c;//若总和相同,则按照c从小到大排序
return d < tmp.d;//若总和c均相同,则按照d从小到大排序
}
}s[N];
int n,cnt;
int main()
{
cin >> n;
//开始枚举并存储c和d的相关信息
for(int c = 0; c * c<= n;c++)
for(int d = c; c*c + d*d <= n;d++)
{
s[cnt++] = {c*c+d*d,c,d};
}
sort(s,s+cnt);
//枚举a和b,并在其中使用二分查找
for(int a = 0; a * a <= n;a++)
for(int b = a; a*a + b*b <= n;b++)
{
//计算出差值,然后去s数组中查找出它
int t = n-a*a-b*b;
int l = 0,r = cnt -1;
while(l <r)
{
int mid = (l+r) >>1;
//和上面几个例题类似,要查找的值t在中点mid的左边,因此调整右端点。
if(s[mid].s >= t) r = mid;
else l = mid+1;
}
//如果找到一组解了,就可以输出结果,因为要字典序最小的
if(s[l].s == t)
{
printf("%d %d %d %d\n",a,b,s[l].c,s[l].d);
return 0;
}
}
}
这里是使用哈希的方式进行查找的代码:
数组模拟的哈希解法
连续刷了这么多怪,休息一会会叭~
🌟例7、第八届蓝桥杯省赛C++A/B组 分巧克力
🌱题目描述
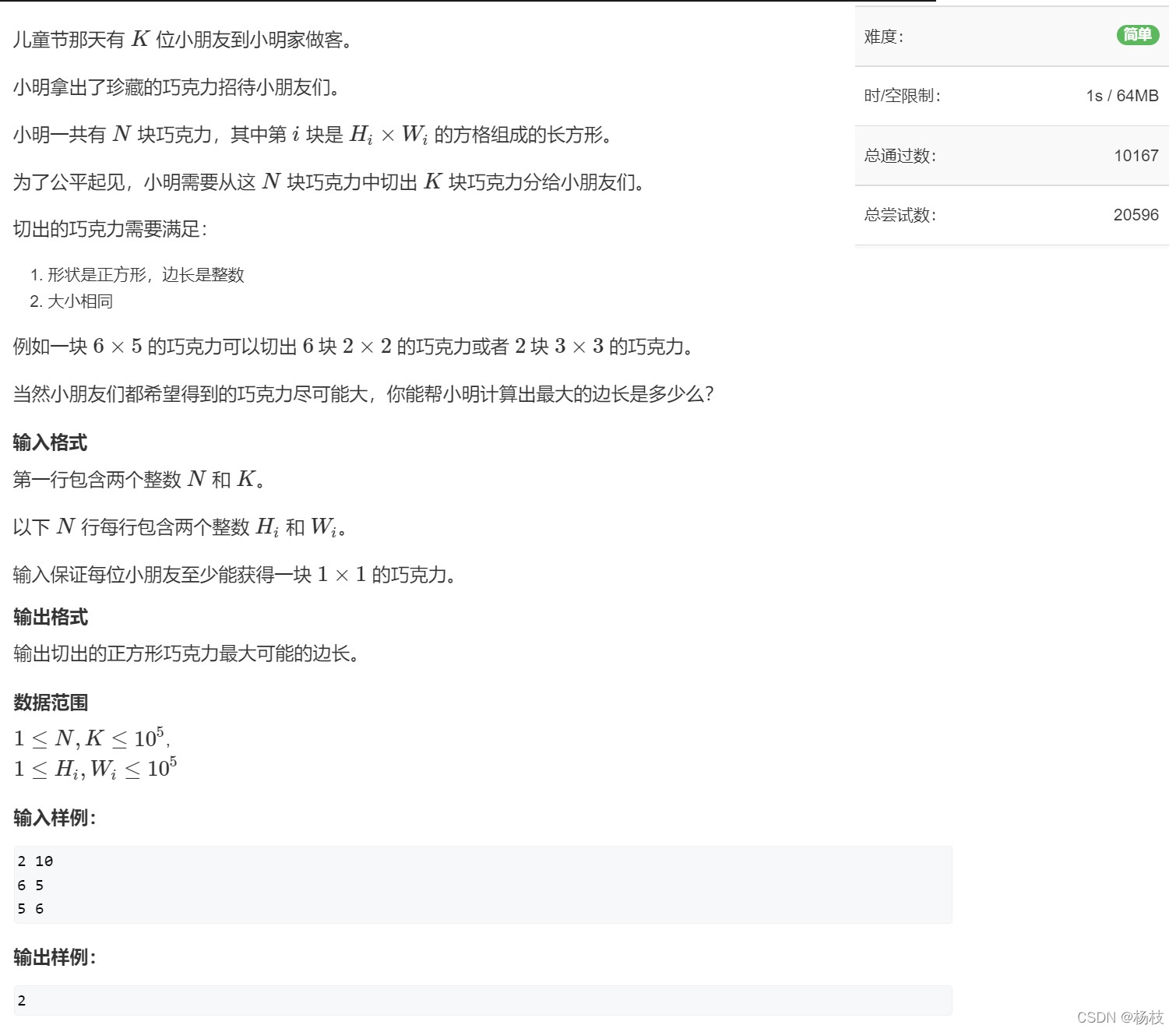
🌴解题报告
这道题了,也是让我们查找到一个合适的边长用于分巧克力。数据范围是十万,用二分去查找这个合适的数据是很容易实现的。
需要注意的细节:
在进行筛选合适的巧克力边长的时候,要分别对
H
[
i
]
H[i]
H[i]和
W
[
i
]
W[i]
W[i]进统计,
即
(
H
[
i
]
/
传入的边长
)
∗
(H[i] / 传入的边长) *
(H[i]/传入的边长)∗
(
W
[
i
]
/
传入的边长
)
(W[i]/传入的边长)
(W[i]/传入的边长).
不能写成:
(
H
[
i
]
∗
W
[
i
]
)
/
(H[i] * W[i])/
(H[i]∗W[i])/
(
传入的边长
∗
传入的边长
)
(传入的边长*传入的边长)
(传入的边长∗传入的边长),这是因为整数除法的向下取整导致精度不准确。
🌵参考代码(C++版本)
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100010;
int h[N],w[N];
int n,k;
bool check(int a)
{
//统计现在这个边长a,能不能分出大于等于题目要求的k块巧克力
int sum = 0;
//枚举n块巧克力的信息
for(int i = 0;i < n;i++)
{
//分别统计h和w中能承载多少个a
sum += (h[i]/a)*(w[i]/a);
if(sum >= k) return true;
}
return false;
}
int main()
{
cin >> n >>k;
//输入n块巧克力的信息
for(int i = 0; i < n;i++) cin >> h[i] >> w[i];
//进去二分环节,查找出合适的尺寸
//输入保证每位小朋友至少能获得一块 1×1 的巧克力。所有左端点最小是1
int l = 1, r = 100000;
while(l < r)
{
int mid = (l+r+1) >> 1;
//如果这个check函数成立,那么证明现在的中点mid应该在要查找的最大边长x左边,
//想要进一步确定x,应该调整左边界。那么上面取mid时候,要补上1
if(check(mid)) l= mid;
else r = mid -1;
}
cout << l <<endl;
}
转眼之间,已经打到第八关了,好快呀
🌟例8、试题 算法训练 搬走要石
🌱题目描述
🌴解题报告
题目要咱们查找到一个最省力的方案,帮助这个相当懒的神仙把石头扔到人间(感觉这个神,缺心眼呀~)
| 要咱们找一个最省力的方案,意思就是以这个方案为分界线,它前面一部分了,不符合要求,它后面一部分了,符合要求了,但是可能不划算了。 |
那么,这个时候,这个题就具备了二段性,咱们就可以屏息运气,打出咱们的二分功法,将这个最省力的方案用二分求出来。
现在唯一要解决的只剩下对 i f if if中判断函数 c h e c k check check的落实。
c h e c k check check函数的运作的核心是判断当前二分出来的这个 m i d mid mid值能否帮助这个懒神仙在规定的 k k k次中搬走所有石头。
🌵参考代码(C++版本)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N=1022;
int n,m;
int a[N];
bool check(int d)
{
int sum = 0,cnt =0,i =1;
//这个check函数检查的是,每次用d的灵力搬石头,是否够在m此中把要石搬完
while(a[i])//当还有石头的时候就继续执行
{
if(sum+a[i] <= d) //这里的意思是判断可以连着搬几块
{
sum += a[i];
i++;
}
//当不能连着搬的时候,检查这块石头是不是直接比灵力大
else if(a[i] > d) return false;//假如是直接比灵力大的情况,那么这个方案不行,直接返回false
else//否则进行下一轮
{
cnt ++; //计数器,用于判断是否在规定的k次中完成任务
sum = 0;//重置sum
}
}
return cnt < m;//判断是否满足最多发动m次灵力
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int l=0,r=1000000;
while(l<r){
int mid= (l+r)/2;
if(check(mid))r=mid;
else l = mid + 1;
}
cout<<l;
return 0;
}
💓总结
好啦好啦,到这里为止,在蝴蝶居中对虫之呼吸贰之型的修习就告一段落了。诸位都没有辜负漂亮的忍姐姐吧
在此也做一个小总结吧:
| 1、对于二分而言,能否使用二分可以从数据范围看出来,也可以在读题之后,可以得知这个答案或者说方案是具有二段性、单调性,那么也一定可以使用二分来做。 |
| 2、二分用得最广的领域应该是查找,因此,当看到题目要咱们查找某个最大、最小的数的时候,就可以打二分的小算盘了。只是也不必局限于二分,哈希同样也在查找中独霸一席天地。暴力枚举能解出来的话,那就更好了 |
3、牢记二分的两种情况
结合着图记忆二分的两种情况;
结合着图记忆二分的两种情况;
结合着图记忆二分的两种情况。
重要的事儿说三遍。
情况一的图是这种啦:
情况二的图则是这种的:
处理好这两种情况的边界问题了,就可以把二分拿捏得好好的啦。
是时候和忍姐姐告别啦,走出蝴蝶屋,准备迈向炼狱先生所在的无限列车啦~

![if(a[mid] >= x) r = mid](/image/aHR0cHM6Ly9pbWctYmxvZy5jc2RuaW1nLmNuL2Y5YjMxMjczZGI2MzRkMDM5ZmNlOGU0ZDU0NDRmNmEwLnBuZz94LW9zcy1wcm9jZXNzPWltYWdlL3dhdGVybWFyayx0eXBlX2QzRjVMWHBsYm1obGFRLHNoYWRvd181MCx0ZXh0X1ExTkVUaUJBNXAybzVwNmQsc2l6ZV8yMCxjb2xvcl9GRkZGRkYsdF83MCxnX3NlLHhfMTYjcGljX2NlbnRlcg%3D%3D)
![if(a[mid] <= x) l = mid ;](/image/aHR0cHM6Ly9pbWctYmxvZy5jc2RuaW1nLmNuL2U3ODE1MzljMzUxMDQ0OTVhNTRiOGI2ZmY1ZmRjYmRiLnBuZz94LW9zcy1wcm9jZXNzPWltYWdlL3dhdGVybWFyayx0eXBlX2QzRjVMWHBsYm1obGFRLHNoYWRvd181MCx0ZXh0X1ExTkVUaUJBNXAybzVwNmQsc2l6ZV8yMCxjb2xvcl9GRkZGRkYsdF83MCxnX3NlLHhfMTYjcGljX2NlbnRlcg%3D%3D)