红黑树与AVL树平衡二叉搜索树的比较与实现

B树与B+树：数据库索引中常用的数据结构

在数据库系统中，高效的索引结构对于查询性能至关重要。B树（B-Tree）和B+树（B+ Tree）是两种广泛应用于数据库索引的数据结构。本文将深入探讨B树与B+树的概念、结构、优缺点，并通过代码实例展示其实现和应用。

一、B树简介

1.1 B树的定义

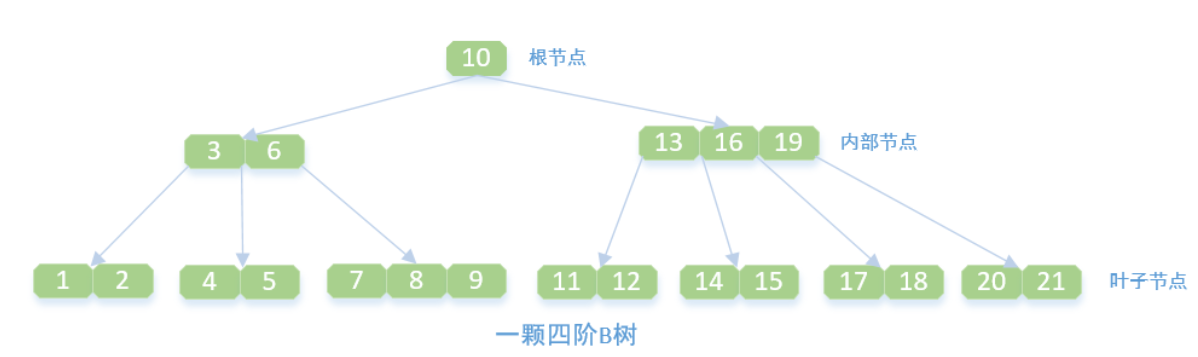
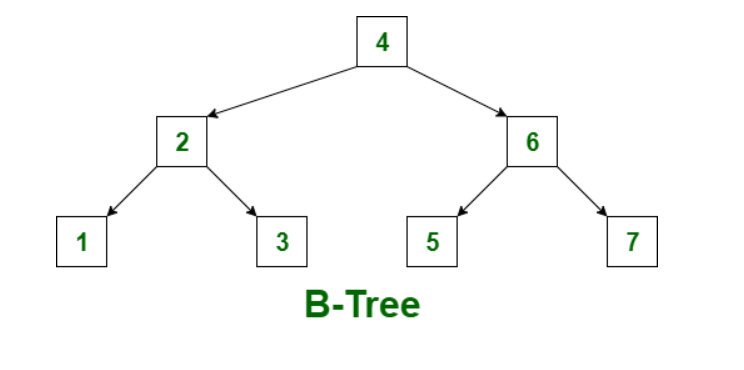
B树是一种自平衡的多叉树，保证了数据的有序性和搜索、插入、删除操作的对数时间复杂度。B树的每个节点可以有多个子节点，且节点内存储的关键字按顺序排列。

1.2 B树的性质

每个节点包含关键字的数量有上限和下限：设B树的阶数为m，则每个节点最多包含m-1个关键字，至少包含⌈m/2⌉-1个关键字（除根节点外）。
根节点至少有两个子节点（除非树为空或只有一个节点）。
所有叶子节点都在同一层次上。
节点中的关键字按升序排列：对于任何节点中的关键字Ki，有Ki-1 < Ki < Ki+1。
子树的关键字范围：如果某节点的关键字为K，则其左子树中所有关键字小于K，右子树中所有关键字大于K。

1.3 B树的操作

插入操作

插入操作需要找到适当的叶子节点，并在插入后保持B树的性质。

class BTreeNode:
    def __init__(self, t, leaf=False):
        self.t = t  # 最小度数
        self.leaf = leaf  # 是否为叶子节点
        self.keys = []  # 节点中的关键字
        self.children = []  # 子节点

class BTree:
    def __init__(self, t):
        self.root = BTreeNode(t, True)
        self.t = t

    def insert(self, k):
        root = self.root
        if len(root.keys) == 2 * self.t - 1:
            temp = BTreeNode(self.t, False)
            temp.children.append(self.root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
            self.root = temp
        else:
            self.insert_non_full(root, k)

    def split_child(self, parent, i):
        t = self.t
        y = parent.children[i]
        z = BTreeNode(t, y.leaf)
        parent.children.insert(i + 1, z)
        parent.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t:(2 * t - 1)]
        y.keys = y.keys[0:(t - 1)]
        if not y.leaf:
            z.children = y.children[t:(2 * t)]
            y.children = y.children[0:(t)]

    def insert_non_full(self, node, k):
        i = len(node.keys) - 1
        if node.leaf:
            node.keys.append(0)
            while i >= 0 and k < node.keys[i]:
                node.keys[i + 1] = node.keys[i]
                i -= 1
            node.keys[i + 1] = k
        else:
            while i >= 0 and k < node.keys[i]:
                i -= 1
            i += 1
            if len(node.children[i].keys) == 2 * self.t - 1:
                self.split_child(node, i)
                if k > node.keys[i]:
                    i += 1
            self.insert_non_full(node.children[i], k)

删除操作

删除操作较为复杂，需要保证删除后仍然满足B树的性质。

1.4 B树的优缺点

优点：

高度平衡，搜索效率高。
插入和删除操作时间复杂度为O(log n)。

缺点：

相对于B+树，叶子节点间没有指针连接，范围查询效率较低。

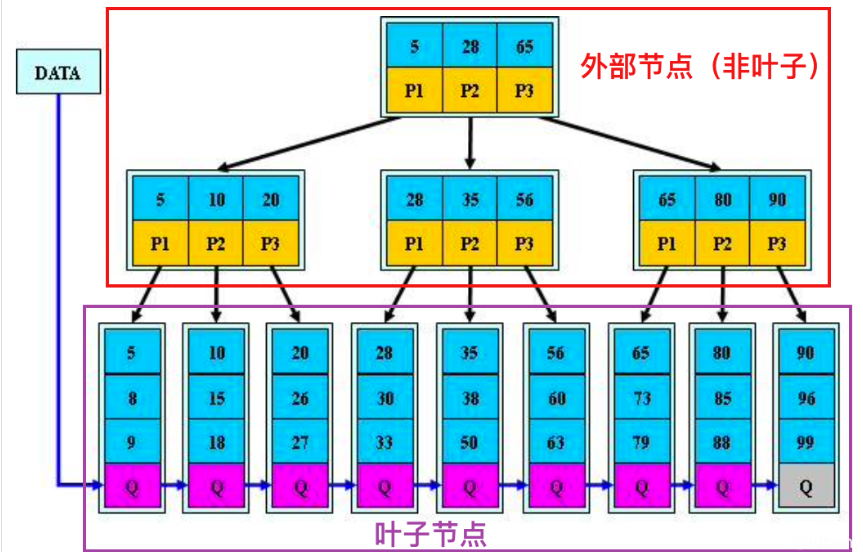
二、B+树简介

2.1 B+树的定义

B+树是B树的变体，其结构与B树类似，但具有一些不同的特性。B+树在数据库索引中应用广泛，特别适合范围查询。

2.2 B+树的性质

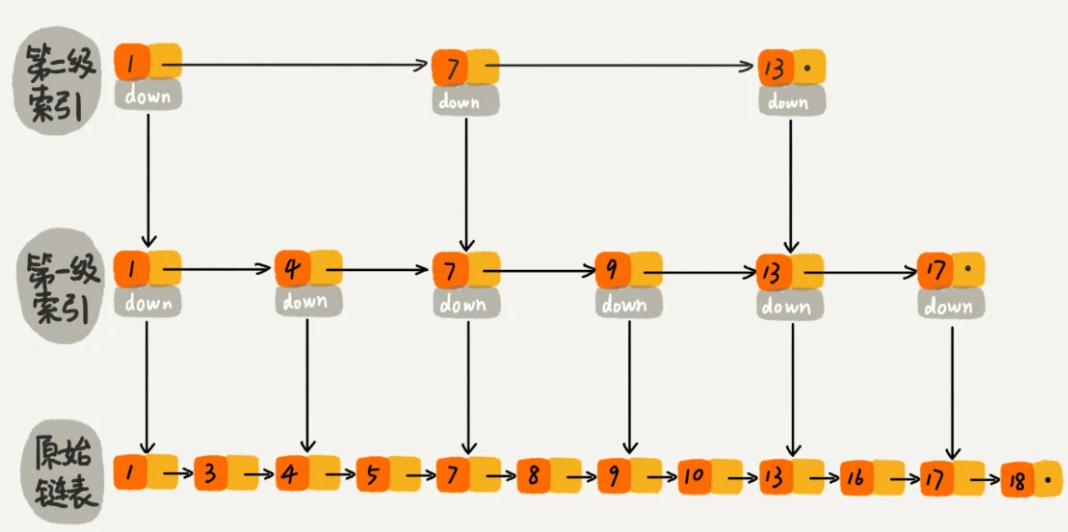
所有数据存储在叶子节点：内节点仅存储键值和子节点指针。
叶子节点按键值顺序排列，并通过链表相连，便于范围查询。
非叶子节点不存储实际数据，仅用于导航。

2.3 B+树的操作

插入操作

插入操作与B树类似，但所有数据插入到叶子节点。

class BPlusTreeNode:
    def __init__(self, t, leaf=False):
        self.t = t
        self.leaf = leaf
        self.keys = []
        self.children = []
        self.next = None  # 指向下一个叶子节点的指针

class BPlusTree:
    def __init__(self, t):
        self.root = BPlusTreeNode(t, True)
        self.t = t

    def insert(self, k):
        root = self.root
        if len(root.keys) == 2 * self.t - 1:
            temp = BPlusTreeNode(self.t, False)
            temp.children.append(self.root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
            self.root = temp
        else:
            self.insert_non_full(root, k)

    def split_child(self, parent, i):
        t = self.t
        y = parent.children[i]
        z = BPlusTreeNode(t, y.leaf)
        parent.children.insert(i + 1, z)
        parent.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t:(2 * t - 1)]
        y.keys = y.keys[0:(t - 1)]
        if y.leaf:
            z.next = y.next
            y.next = z
        else:
            z.children = y.children[t:(2 * t)]
            y.children = y.children[0:(t)]

    def insert_non_full(self, node, k):
        i = len(node.keys) - 1
        if node.leaf:
            node.keys.append(0)
            while i >= 0 and k < node.keys[i]:
                node.keys[i + 1] = node.keys[i]
                i -= 1
            node.keys[i + 1] = k
        else:
            while i >= 0 and k < node.keys[i]:
                i -= 1
            i += 1
            if len(node.children[i].keys) == 2 * self.t - 1:
                self.split_child(node, i)
                if k > node.keys[i]:
                    i += 1
            self.insert_non_full(node.children[i], k)

2.4 B+树的优缺点

优点：

叶子节点通过链表相连，范围查询效率高。
非叶子节点仅存储键值，内部节点容量更大，有利于减小树的高度。

缺点：

实现较为复杂。

三、B树与B+树在数据库索引中的应用

3.1 B树的应用场景

B树适用于读写操作频繁且查询效率要求高的场景，例如：

文件系统索引
一些嵌入式数据库

3.2 B+树的应用场景

B+树特别适合范围查询和顺序访问频繁的场景，例如：

大型数据库系统（如MySQL、PostgreSQL）
文件系统（如NTFS）

四、B树和B+树的性能对比

4.1 查询性能

B树和B+树在查询性能上有一些差异：

B树：在B树中，查找一个键值需要从根节点开始，逐层向下查找，直到找到目标键值或达到叶子节点。由于所有节点都存储数据，查找路径上的每个节点都可能是目标节点，这增加了查找操作的复杂性。
B+树：在B+树中，所有实际数据都存储在叶子节点，内节点只用于导航。因此，查找操作最终总是到达叶子节点，这使得查找路径更为简单。此外，叶子节点之间通过链表连接，便于顺序查找和范围查询。

def search_btree(node, k):
    i = 0
    while i < len(node.keys) and k > node.keys[i]:
        i += 1
    if i < len(node.keys) and k == node.keys[i]:
        return node  # 找到关键字
    if node.leaf:
        return None  # 未找到关键字
    return search_btree(node.children[i], k)

def search_bplustree(node, k):
    while not node.leaf:
        i = 0
        while i < len(node.keys) and k > node.keys[i]:
            i += 1
        node = node.children[i]
    for key in node.keys:
        if key == k:
            return node  # 找到关键字
    return None  # 未找到关键字

4.2 插入性能

插入操作在B树和B+树中均涉及节点的分裂：

B树：插入操作时，如果目标叶子节点已满，需要分裂该节点，并将中间键值提升到父节点。如果父节点也已满，则递归分裂，直到根节点。分裂操作复杂度较高，但由于每个节点都存储数据，分裂次数相对较少。
B+树：插入操作时，数据始终插入到叶子节点。如果叶子节点已满，需要分裂该节点，并将中间键值提升到父节点。由于内节点只存储键值，节点的利用率更高，但叶子节点分裂较为频繁。

4.3 删除性能

删除操作在B树和B+树中都较为复杂，需要保持树的平衡：

B树：删除操作需要找到目标键值，并根据情况调整树结构。如果删除的是非叶子节点的键值，需要用前驱或后继键值替换，保证树的有序性。若节点不足，需合并或借用兄弟节点的键值。
B+树：删除操作始终在叶子节点进行，若节点不足，同样需要合并或借用兄弟节点的键值。内节点的调整相对简单，因为不存储实际数据，只需更新键值和指针。

4.4 范围查询性能

范围查询是B+树的强项，尤其适合顺序访问：

B树：范围查询需要在多个子树间跳转，不连续的存储方式使得范围查询效率较低。
B+树：叶子节点通过链表相连，可以快速遍历所有符合条件的节点，极大提升了范围查询的效率。

def range_query_bplustree(node, k1, k2):
    result = []
    leaf = search_bplustree(node, k1)
    if not leaf:
        return result
    while leaf:
        for key in leaf.keys:
            if k1 <= key <= k2:
                result.append(key)
            elif key > k2:
                return result
        leaf = leaf.next
    return result

五、应用实例

5.1 数据库索引

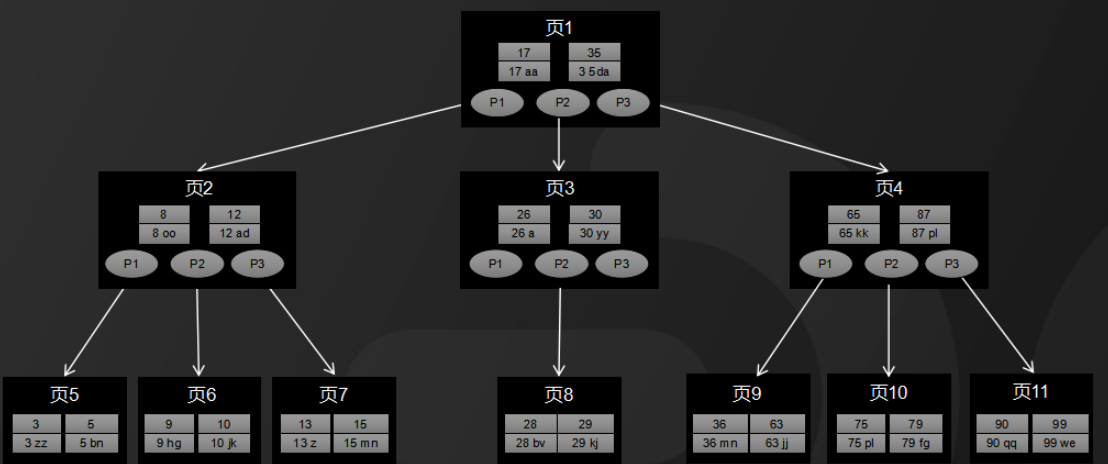
数据库索引是B树和B+树的经典应用场景。通过索引，可以显著提高数据查询速度。以MySQL为例，InnoDB存储引擎默认采用B+树结构作为索引：

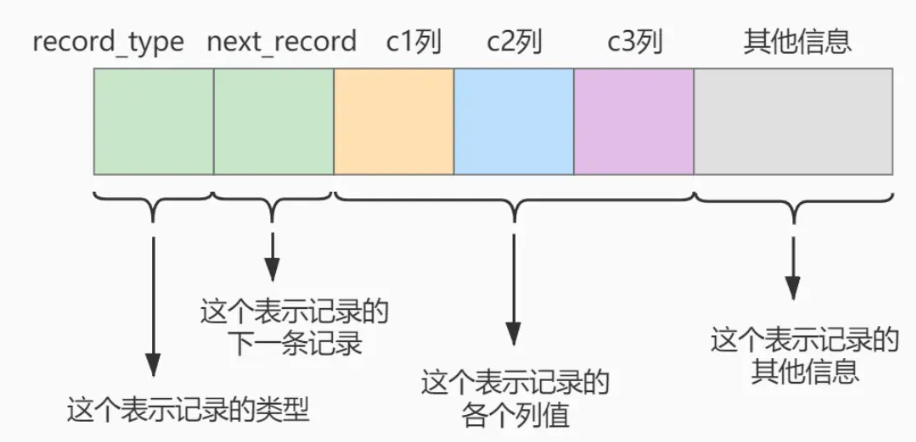
主键索引：主键索引是一种聚集索引，索引文件与数据文件存储在一起，叶子节点存储行数据。
辅助索引：辅助索引是一种非聚集索引，叶子节点存储主键的值，通过主键访问行数据。

CREATE TABLE example (
    id INT AUTO_INCREMENT PRIMARY KEY,
    data VARCHAR(255),
    INDEX (data)
);

在上述例子中，id列是主键索引，data列是辅助索引。通过B+树结构，MySQL能够快速定位数据，提高查询性能。

5.2 文件系统

文件系统中的目录结构和文件索引也广泛应用B树和B+树。例如，NTFS文件系统采用B+树作为其索引结构，用于存储文件名和文件数据块的位置。通过B+树，文件系统能够高效地执行文件查找和数据读取操作。

class FileSystem:
    def __init__(self, t):
        self.index = BPlusTree(t)

    def create_file(self, filename, data):
        self.index.insert(filename)
        # 存储文件数据的操作

    def find_file(self, filename):
        return search_bplustree(self.index.root, filename)

fs = FileSystem(3)
fs.create_file("example.txt", "Hello, World!")
print(fs.find_file("example.txt"))

六、B树和B+树的实现细节

6.1 B树的实现

B树的实现主要包括插入、删除和查找操作。在实际应用中，B树的每个节点通常存储多个键值和子节点指针，保证节点的高度平衡。

6.2 B+树的实现

B+树的实现与B树类似，但在插入和删除操作时需要特别处理叶子节点之间的链表连接。此外，B+树的叶子节点存储所有数据，内节点仅用于导航。

class BPlusTreeNode:
    def __init__(self, t, leaf=False):
        self.t = t
        self.leaf = leaf
        self.keys = []
        self.children = []
        self.next = None

class BPlusTree:
    def __init__(self, t):
        self.root = BPlusTreeNode(t, True)
        self.t = t

    def insert(self, k):
        root = self.root
        if len(root.keys) == 2 * self.t - 1:
            temp = BPlusTreeNode(self.t, False)
            temp.children.append(self.root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
            self.root = temp
        else:
            self.insert_non_full(root, k)

    def split_child(self, parent, i):
        t = self.t
        y = parent.children[i]
        z = BPlusTreeNode(t, y.leaf)
        parent.children.insert(i + 1, z)
        parent.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t:(2 * t - 1)]
        y.keys = y.keys[0:(t - 1)]
        if y.leaf:
            z.next = y.next
            y.next = z
        else:
            z.children = y.children[t:(2 * t)]
            y.children = y.children[0:(t)]

    def insert_non_full(self, node, k):
        i = len(node.keys) - 1
        if node.leaf:
            node.keys.append(0)
            while i >= 0 and k < node.keys[i]:
                node.keys[i + 1] = node.keys[i]
                i -= 1
            node.keys[i + 1] = k
        else:
            while i >= 0 and k < node.keys[i]:
                i -= 1
            i += 1
            if len(node.children[i].keys) == 2 * self.t - 1:
                self.split_child(node, i)
                if k > node.keys[i]:
                    i += 1
            self.insert_non_full(node.children[i], k)

七、总结

B树和B+树作为数据库索引中常用的两种数据结构，各自具备独特的优势和适用场景。B树凭借其高效的搜索、插入和删除操作，适用于一般的读写操作，且结构相对简单。然而，由于其叶子节点之间没有连接，B树在范围查询上的表现不如B+树。

B+树在范围查询和顺序访问中表现出色，是大型数据库系统中的首选结构。其叶子节点通过链表相连，使得范围查询和顺序扫描变得高效且直观。此外，B+树的内节点仅存储键值，数据存储在叶子节点，使得内节点的利用率更高，树的高度更低。

通过代码实例，本文详细介绍了B树和B+树的插入、查找和范围查询操作，展示了其在数据库索引和文件系统中的实际应用。B树适用于文件系统索引和一些嵌入式数据库，而B+树则被广泛应用于大型数据库系统（如MySQL、PostgreSQL）和文件系统（如NTFS）。

理解和合理选择这两种数据结构，对于优化数据库性能和效率至关重要。B树和B+树在数据库系统中的应用不仅提高了查询速度，还增强了数据管理的灵活性和可靠性。在未来的数据结构研究和应用中，B树和B+树仍将继续发挥重要作用，为大数据处理和存储提供强有力的支持。