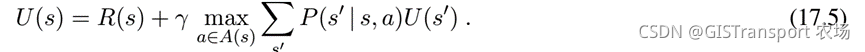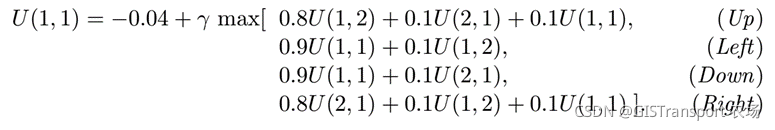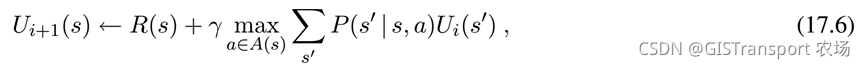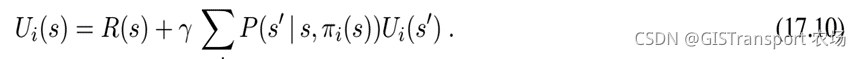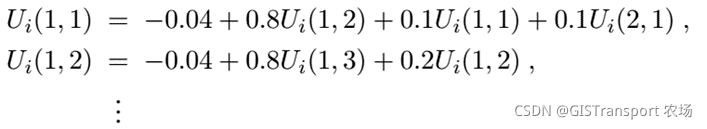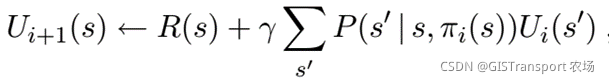在学习强化学习之前，首先介绍一个概念叫马尔科夫决策过英文全称为Markov decision process（MDP）。理解该概念对于强化学习的理解具有重要帮助。好了，下面开始。

一、Markov decision process

     马尔科夫决策过英文全称为Markov decision process（MDP）它是指在fully observable、stochastic environment 环境下的序列决策(sequential decision)问题，其中涉及Markovian transition 和 additive rewards。涉及的几个概念下面先描述一下：

-Agent：一个agent可以看作是任何可以通过传感器感知环境，并通过其执行器（actuators）来执行动作的事物。

-Fully observable: 如果一个agent的传感器可以感知环境的完整状态，我们称为当前的任务环境是fully observable, 反之则称之为partially observable。

-Stochastic 相对应是deterministic，如果环境的下一个状态完全由当前的状态和动作决定，我们称其为deterministic，反之则为stochastic。

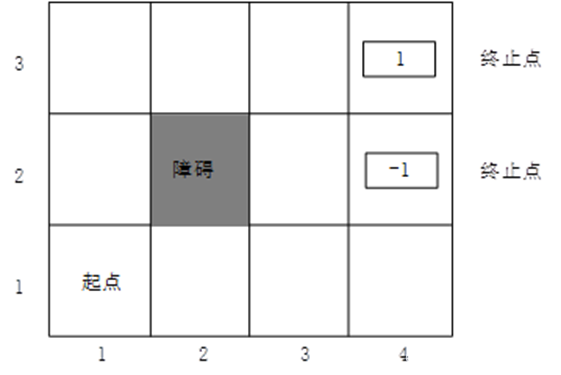
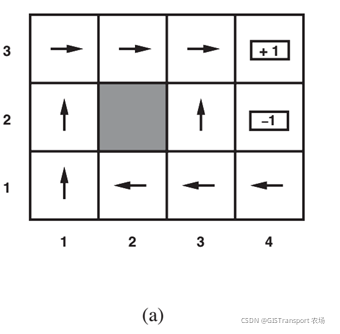
       看完以上描述是不是彻底懵逼了，如果没看懂让我们先把这概念放一放，从一个实例来解释序列决策问题。假设有如下所示的4*3格网（即当前的任务环境），我们玩一个游戏，将Agent放在起点（1, 1）的位置，其目标是agent 通过执行上下左右四个动作来找到一条从该起点到终点（4,3）路线，Agent到达该点后游戏结束。注意其中（4, 2）也被标记为终止点，该点并非我们的目标点，但是如果Agent不小心走错了到这个位置，游戏也会结束。

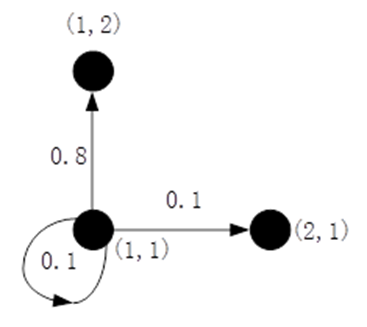
       为了让Agent能够做出合适的动作，这里我们根据每个网格的情况给他设定相应的奖励，如上图所有，我们将终点（4,3）和（4,2）的奖励分别设置为1和-1。其余除（2,2）以外，其奖励设置为-0.04，（2,2）由于是障碍物其奖励为None。Agent的目的就是找到一条奖励最高的路线，接下来就是采用一个数学公式对奖励进行建模，在论述这个问题之前我们先回到问题本身。Agent 从起点到终点可以看作是一个状态转移的过程，即重复从一个状态转移到下一个状态的过程，直到抵达终止的状态。在每个状态转移的过程，Agent 可以选择上下左右4个动作之一。由于我们之前提到过当前的任务环境是stochastic，也就是说即使明确了当前的状态并选定了一个状态，也不能够完全确定下一个状态。这里假设我们选定一个动作后，agent有80%的概率执行该动作抵达下一个状态，另有20%的概率沿着选定动作的垂直方向到达下一个动作来模拟当前在stochastic 环境下的不确定性。比如说：当前状态是（2,2），假设我们选定动作“上”这个动作，那么其对应的转移概率如下图所示。其他动作与此类似，不再累述。

       好了，了解了状态转移过程之后，我们就可以正式定义当前的问题，我们的目的是为了给一个状态序列(state sequence) ， 找到一个策略π（policy），策略为每个状态s推荐一个动作 π(s) 来使得我们最后的效用（utility）最高，效用形式如下： 

      其中R(s)表示状态s对应的奖励（reward）。其中的γ≤1， 表示的是一个折扣，当γ=1时表示的是累加形式的reward，γ<1 表示的是discounted 形式的reward。很明显，我们的目标是选定一个策略使得效用到达最大。由于环境是stochastic ，所以我们首先计算效用值的期望（expected utility）：

        由此，我们的目标就可以明确定义为：找到一个策略π，来最大化，其中策略是指为每一个state推荐一个动作。

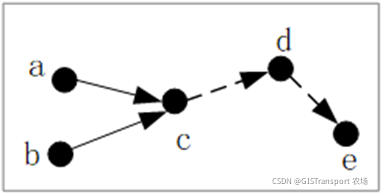
         为每一个state 推荐一个action，他和s的关系是当s为起始状态时，为对应的最优策略。对于以discount 形式的utility而言，其突出的优点是最优解决方案实际上和开始状态无关，即不管是从哪个状态开始，这个方案都是最优（记住这个重要结论，证明略）。比如说  和 分别是起始于状态a 和状态b的最优解决方案，两者同时经过c，对于a，b而言，c之后解决方案肯定是固定的。当然，这一点非discount形式的reward结合方式并不成立（证明略）。因此，我们可以直接将最优方案可以直接写成π*。

      因此，对于一个状态s，其真实的utility是，即当执行最优policy后对应discounted reward的期望总和，这里简写为。注意，是指从s开始往后所有state的效用，而reward R(s)指的当前状态s对应的奖励。

        以上定义的utility函数使得我们可以通过最大expected utility 来决定对所有动作的选择。也就是说，选择的动作必须使得随后那一个动作得到最大效用值（一个迭代的关系）。

        其中表示在状态s下执行动作a得到状态 s' 的概率。好了，那么这个问题具体如何求解呢，下面我们介绍一种常见的求解方式，即基于value iteration 的optimal policy selection。

二、基于value iteration的optimal policy 选择

       基本思路是计算每一个state的utility，然后基于所有state utilities为每一个state选择一个最优动作。

2.1 Bellman equation for utilities

      上一个定义一个state的utility为：从当前的状态开始discount reward总和期望值。基于此，在假设state选择最优动作的条件下，单个状态的utility是它的即时reward加上他下一个state的最大discounted utility。

以上等式被称之为Bellman等式。等式17.2中所定义的s之后所有状态对应的expected utility是Bellman等式对应的解。另外，这个最优解同时也是唯一的。

例如，下面的等式表示的图17.3中4*3格子中(1, 1)对应utility等式：

通过上面的等式可知，最优的动作为up。

2.2 价值迭代算法（ value iteration algorithm）

        对于MDPs问题，假设共有n个状态未知的utilities。由于等式中涉及大max 运算，所以该问题是非线性的。因此，可以采用迭代的方式来对该问题进行求解。求解的方式是首先给每个state设置一个随机的U值。令为状态s在第 i 次迭代的utility。

 具体算法的伪代码描述如下：

        上述的迭代中，在一次迭代中采用的是对所有的state同时进行更新，通过多次迭代state的utility，最终将实现收敛，成为Bellman equation的解（且为唯一解）。

2.3  Policy iteration

        上一节中我们讨论了基于价值迭代policy求解方式，这一节介绍另一种基于策略迭代求解方法。我们假设随机给定一个策略π0，然后通过迭代的方式对这个策略进行优化。在进行优化之前，我们需要了解两个概念，分别是策略评估和策略提升。

Policy evaluation：给定一个policy ，计算，其中是一个多维度向量（向量的维度等于总的状态数量），表示执行后每个state对应utility。

Policy improvement：基于公式17.4 来对计算每个state对应的新动作，进而得到迭代后策略。

以上算法在policy improvement对utility不产生变化时停止，即达到最优。具体算法如下：

 对于policy iteration的执行，其对应的Bellman equation中状态s和其邻接状态的关系如下：

 比如说下图，我们有 ,  ，

 因此有以下等式：

        由于policy 预先知道，以上函数中没有max 操作，因此可以直接进行线性求解（n个方程和n个未知数）。其算法复杂度为 ，对于n比较小的问题可以直接采用线性方程进行求解。但是对于n比较大问题，可以采用一种简化的value iteration （因为action 固定，所以称之为简化）来对utilities做一个近似求解。简化版的Bellman update如下：

上面的更新被执行K次来获取下一个utilities的估计，其对应算法称之为modified policy iteration。
       以上value iteration 和 policy iteration 均是采用对所有状态的policy或者是utility同时进行更新的方式。但也并非严格要求如此。实际上可以选取部分states然后采用两种更新方式中的一种对其进行更新，这种方式被称之为异步更新，且最后也会达到收敛。

后记：

        接下来的两篇博文将通过python 分别将 value iteration 和 policy iteration 算法进行实现，代码如下：

          （1）价值迭代算法求解MDP实现 value iteration algorithm（MDP之二）

          （2） 策略迭代算法求解MDP实现（之三）