Log

2022.01.04今天先开个头，明天继续
2022.01.05继续弄感觉好理解，但是东西有点多
2022.01.06白天要搞别的事，晚上来学
2022.01.07收个尾

一、基本操作（basic operations）

1.基本运算

• 注释用百分号%。
• help functionName：显示指定函数的帮助函数。
• exit or quit ： 退出 Octave。

①加减乘除幂

• 5 + 6 ⇒ 11
• 3 - 2 ⇒ 1
• 5 * 8 ⇒ 40
• 1 / 2 ⇒ 0.50000
• 2 ^ 6 ⇒ 64

②逻辑运算

• 相等：1 == 2 ⇒ 0
  1 等于 2 判断为假，false 用 0 表示
• 不等：1 ~= 2 ⇒ 1
  1 不等于 2 判断为真，true 用 1 表示
• 逻辑与：1 && 0 ⇒ 0
• 逻辑或：1 || 0 ⇒ 1
• 异或运算：XOR(1,0) ⇒ 1

③更改提示符

• 一般Octave提示符显示版本以及其它信息，可以通过PS1(">>")语句将其改为>>

2.变量操作

①变量赋值

• a = 3 变量 a 赋值为 3 ，屏幕显示。
  a = 3; 变量 a 赋值为 3 ，末尾添加分号（semicolon），屏幕不显示。
• b = 'hi'字符串赋值
• c = (3>=1) 表达式赋值

②变量查询/输出信息

• 可以通过输入变量名直接查询其存储的信息：
  a = pi; ，a ⇒ a = 3.1416
• 通过disp函数输出相应数值：
  a = pi; ，disp(a) ⇒ 3.1416
• 通过更加复杂的方式输出字符串：
  disp(sprintf('2 decimals: %0.2f', a)) ⇒ decimals: 3.14
disp(sprintf('6 decimals: %0.6f', a)) ⇒ decimals: 3.141593
• 字符串显示默认的位数：
  format long ， a ⇒ a = 3.14159265358979
• 打印少量的小数点后位数：
  format short ， a ⇒ a = 3.1416

3.向量和矩阵

①建立矩阵

• 创建矩阵：A = [1 2; 3 4; 5 6]
  等价方式：A = [1 2; ，3 4;，5 6]
  （分号让矩阵换到下一行）
• 行向量：V = [1 2 3]
• 列向量：V = [1; 2; 3]

②生成矩阵的快捷方法

• V = 1:0.1:2
  说明：行向量 V 从 1 开始，0.1 为步长，到 2 停止，即建立一个 1×11 维的矩阵
• V = 1:6
  说明：行向量V = [1 2 3 4 5 6]
• zeros(1,3)
  说明：建立一个 1×3 的矩阵，每个元素都为 0
• ones(2,3)
  说明：建立一个 2×3 的矩阵，每个元素都为 1
• C = 2 * ones(2,3)
  说明：建立一个 2×3 的矩阵 C，每个元素都为 2
• rand(m,n)
  说明：随机生成一个 m×n 维的矩阵，每个元素介于 0 和 1 之间
• randn(m,n)
  说明：随机生成一个 m×n 维的矩阵，且所有元素服从高斯分布/正态分布（Gaussian/Normal distribution），均值（mean）为0标准差（variance）或者方差（deviation）为1

③绘制矩阵直方图

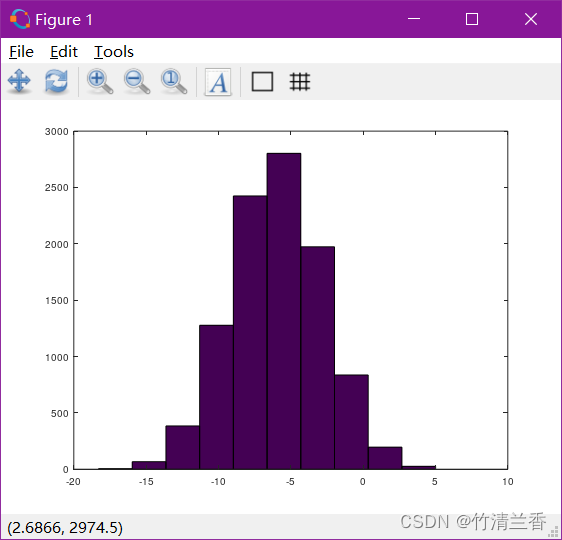
• w = -6 + sqrt(10) * (randn(1,10000))
• hist(w)
  绘制直方图（histogram）：
  
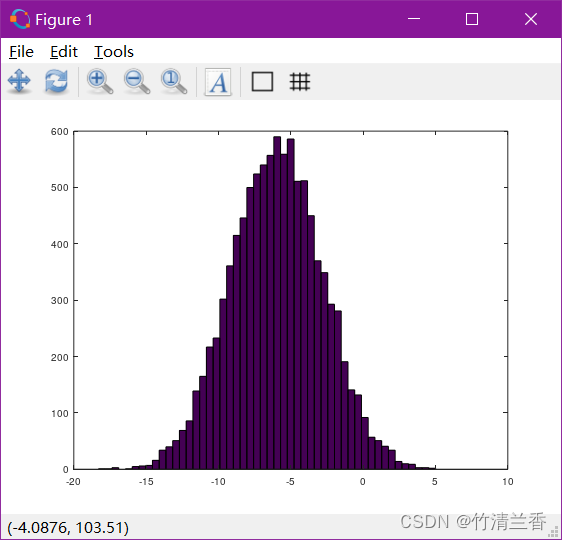
• hist(w,50)
  更多竖条（buckets） 的直方图：
  

④生成矩阵的特殊方法

• eye（n）：生成 n 阶单位矩阵

二、移动数据（move data around）

1.计算矩阵大小

• A = [1 2; 3 4; 5 6]
• size(A) ⇒ ans = 3 2
  表示 A 的大小为 3×2，同时，该结果也可以看作是一个新的 1×2 维的矩阵，即：
  size(size(A)) ⇒ ans = 1 2
• size(A,1)：返回 A 的第一维度大小，即行数
• size(A,2)：返回 A 的第二维度大小，即列数
• length(A)：返回 A 的最大维度大小

2.在文件系统中加载和查找数据

①数据加载/保存

• pwd：显示当前所在路径
• cd：更改路径
• ls：列出当前路径下的文件
• load fileName or load('fileName') ：将指定文件加载到 Octave 中（文件中的所有内容被看做是一个变量）
• who ：显示当前 Octave 中储存的所有变量
• whos ：显示当前 Octave 中储存的所有变量的详细信息（包括变量名、维度大小、内存大小、变量类型）
• clear v ： 删除变量 v
• clear ： 删除内存中所有内容
• A = B(1:10) ： 将 B 的前 10 个元素赋给 A（超出范围会有报错）
• save hello.mat v ： 将变量 v 保存到文件 hello.mat 中（文件不存在会自动创建，重复写入不同信息会覆盖原有内容，这里就可以发现和加载文件的命令是存在着一定关联的）
• save hello.txt v -ascii ： 数据储存成 ASCII 编码的文档（即文本文档），不加最后一个字段默认是以二进制存储，如果数据很大还会对其进行压缩（咱觉得是用一种编码压缩的方式，加载的时候还会进行解码）

②数据查找/矩阵赋值/矩阵合成

A 是一个 3×2 维的矩阵

• A(3,2) ：查找矩阵 A 中第三行第二列的元素（和从0开始的数组下标索引不同）
• A(2,:) ：查找矩阵 A 中第二行的所有元素，此处 : 代表该行的所有元素（也可以用来代表一列，如 A(:,2)）
• A([1 3],:) ：第一索引为 1 ，第二索引为 3 ，即查找 A 中第 1 行和第 3 行的所有元素
• A(:,2) = [10; 11; 12] ： 对 A 的第二列数据进行重新赋值
• A = [A, [100; 101; 102]] ： 在 A 后面添加一列数据（感觉和字符串很像：str = str + ‘s’）。当然，如果数据与维数不匹配是会报错的。
• A = [A; [100; 101]] ： 以此类推，把 , 换成 ; 就是添加新行。
• A(:) ： 把 A 放入一个单独的向量中
• C = [A B] / C = [A; B] ：合成 A B （左右/上下）

三、计算数据（do computational operations on data）

1.矩阵基本运算

• A * B ： 矩阵 A 与矩阵 B 相乘
• A .* B ： 矩阵 A 中的每一个元素与矩阵 B 中对应的元素相乘（一一对应）， . 点号（period） 表示对元素（element-wise） 的运算
• -A <==> -1 * A
• A .^ 2 ：A 中每个元素平方（squaring） （“ ^ ”，caret，脱字符号 （中文尚无通用名称））
• 1 ./ A ：A 中每个元素取倒数（inverse）
• log(A) ：对 A 中每个元素进行对数运算（logarithm）
• exp(A) ：以 e 为底，A 中元素为指数的幂运算（exponentiation）
• abs(A) ： 求 A 中所有元素的绝对值（absolute value）
• v + ones(length(v),1) <==> v + 1 ： v 中每个元素加 1（矩阵向量皆可）
• A + ones(size(A))<= =>A + ones(length(v),1) <= => A + ones(length(v),2) <==> A + 1 ： 同上（A 为 3×2 矩阵，A + ones(length(v),3)就不行，不是很理解A + ones(length(v),1)加一个 3×1 的矩阵可以把所有 3×2 的元素都加上）

2.矩阵其他运算

• A' ： 求 A 的转置（transpose），（A’——A prime）（'，撇号，apostrophe symbol，左引号，left quote）
• val = max(A) ： 返回 A 中最大元素的值
• [val, ind] = max(A) ： val 为中最大元素的值，ind 为最大值的索引（试了一下， A 为向量时还比较好理解，A 为 3×2 的矩阵时 val 是一个 1×2 维的向量，不是很理解）
• A < 3 ： 让 A 的每个元素进行比较，返回一个相同维度的矩阵，对应位置用 0 和 1 表示真假。
• find(a < 3) : 返回满足条件元素的下标索引
  （嘿嘿，Markdown中<3⇒ ❤️ 。有意思）
  以下 A 为 3 阶矩阵
• magic(n) ： 返回名为幻方（magic square） 的 n 阶矩阵，任意行、列、对角线中的元素相加值相同（每次 Octave 给出的 n 阶幻方都是固定的，不知道阶数确定时幻方是不是唯一的）
• [r, c] = find(A >= 7) ： r 为行地址索引，c 为列地址索引
• sum(a) ： 对 a 中所有元素求和
• sum(A, 1) ： 对 A 的每一列求和
• sum(A, 2) ： 对 A 的每一行求和
• prod(a) ： 返回所有元素的 乘积（product）
• floor(a) ： 所有元素向下取整（舍去小数部分）
• ceil(a) ： 向上取整（向上最接近的整数）
• max(rand(3),rand(3)) ： 返回取二者中元素较大者构成的一个新矩阵
• max(A, [], 1) ：得到每一列的最大值，其中 1 代表从第 1 维度取值
• max(A, [], 2) ：得到每一行的最大值，其中 2 代表从第 2 维度取值
• max(A) ：默认求每一列的最大值
• max(max(A)) ：求 A 中元素的最大值
• max(A(:)) ：同上，A(:) 表示 A 以一个向量的形式调用
• sum(sum(A. *eye(9))) ： 对矩阵的主对角线进行求和运算
• flipud(A) ： 使矩阵垂直翻转（flip up down）
• sum(sum(A. *flipud(eye(9)))) ： 对矩阵的次对角线进行求和运算

四、数据绘制（plotting data）

下面将要介绍一些 Octave 工具来绘图并可视化数据（plotting and visualizing data）

• 先初始化一点数据：

  • t = [0: 0.01: 0.98];
  • y1 = sin(2*pi*4*t);
  • y2 = cos(2*pi*4*t);

• 绘制正弦函数（sine function） ：plot(t, y1);

• 绘制余弦函数（cosine function） ：plot(t, y2);

• 使两条图像重合的方式如下：

  • plot(t, y1);
  • hold on; ： 保留原有图像，在其基础上继续画（一次就足够，后面再加函数原图像仍然保留）
  • plot(t, y2, 'r'); ： 'r' 使该曲线为红色（red），加以区分

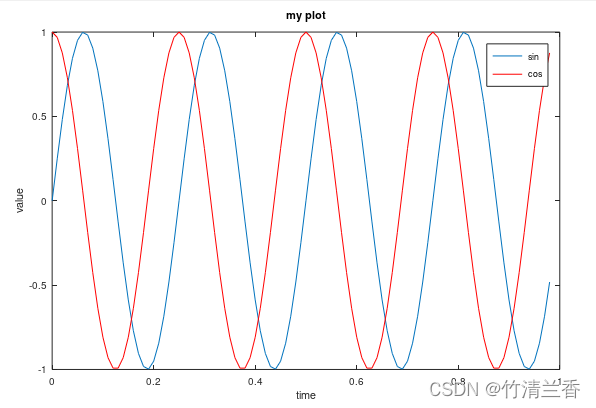
• 继续对当前图像进行处理：

  • xlabel('time') ： 添加 x 轴标签（label）
  • ylabel('value') ： 添加 y 轴标签（label）
  • legend('sin', 'cos') ： 标记（label）当前的两个函数，将图例（legend） 放在右上角（upper right）
  • title('my plot') ： 在图像（figure）的顶部添加标题
    

• 最后还可以保存当前图像：print -dpng 'myPlot.png'

• 可以通过 help plot 查看将图像保存为其他格式的方法

• close ： 关闭图像

• 为图像标号（specify a figure numbers）:

  • figure(1); plot(t, y1);
  • figure(2); plot(t, y2);

• subplot(1, 2, 1); ： 将图像分为一个1*2的格子（参数1和参数2），使用第一个格子（参数3）

• axis([0.5 1 -1 1]) ： 设置 x 轴和 y 轴的范围

• clf; ： 清除一幅图像

• imagesc(A) ：绘制矩阵，不同颜色代表不同的值

• imagesc(A), colorbar, colormap gray; ： 生成一个彩色图像、一个灰度分布图，并在图像右侧加入一个颜色条，展示不同深度的颜色对应的数值。可以通过 , 逗号将多条语句写入同一行中。

五、控制语句（control statements）

1. for 语句

• v = zeros(10, 1)
• for i=1:10, ：从 1 遍历到 10
      v(i) = 2^i;
end;
• 也可以这样写从 1 到 10 的循环：
  indices = 1:10;
for i=incides,
    disp(i);
end;
• break 和 continue 在 Octave 中也可以使用

2. while 语句

• i = 1;
while i <= 5,
    v(i) = 100;
    i = i + 1;
end;
• 用上了 if 和 break：
  i = 1;
while true,
    v(i) = 999;
    i = i + 1;
    if i == 6,
        break;
    end;
end;

3. if-else 语句

• if v(1)==1,
    disp('The value is one');
elseif v(1)==2,
    disp('The value is two');
else,
    disp('The value is not one or two');
end;

4. 定义并使用函数

①基本

• 预先建立后缀为 .m 的文件，并以函数名作为文件名： functionName.m，例如 squareThisNumber(x) 。编辑其内容最好用文本编辑器进行（因为默认的记事本打开可能会把间距弄得很乱）
• 函数内容的说明：
  function y = squareThisNumber(x) ： 返回一个值存到 y 里，且函数有一个自变量 x
  y = x^2 ：定义函数的主体
• 只要文件在 Octave 当前的路径下，就可以直接通过函数名调用函数
  
• 除此之外， Octave 还允许定义的函数有多个返回值，如：
  function [y1, y2] = squareAndCubeThisNumber(x)
y1 = x^2;
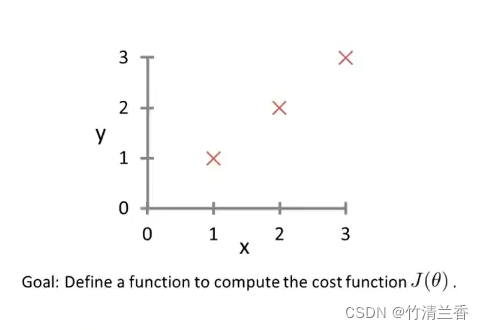
y2 = x^3;
• 再来一个稍微复杂一点的例子，如下图给出训练集求代价函数：
  
• 首先在 Octave 中初始化数据：
  X = [1 1; 1 2; 1 3]
y = [1; 2; 3]
theta = [0; 1]
• 定义函数 costFunctionJ.m ：

function J = costFunctionJ(X, y, theta)

% X is the "design matrix" containing our training examples.
% y is the class labels

m = size(X, 1);					% number of training examples
predictions = X*theta;			% predictions of hypothesis on all m examples
sqrErrors = (predictions-y).^2; % squared errors

J = 1/(2*m) * sum(sqrErrors);

• 调用函数：
  j = costFunctionJ(X, y, theta)
• 得到的结果为 j = 0 ，表示完美拟合
• 如果 theta = [0; 0] ，得到结果为 j = 2.3333 ，说明并不能很好的拟合，该结果实际上就是每个样本的平方差之和再除以 2m ，即 (1^2 + 2^2 + 3^2) / (2*3)

②进阶

• addpath('C:\path\...') ： 将指定路径添加到 Octave 的搜索路径，当切换到其他路径时仍然可以调用添加的路径下的函数（只在一次中有效，即退出 Octave 重新进入时需要重新添加路径）

六、向量化（vectorization）

1.简述

• Octave 、 MATALAB、 Python NumPy、Java、 C、 C++这些语言都具有内置的或者易获取的各种线性代数库（linear algebra libraries） ， 都已经实现了高度优化，如果能够利用好他们（或者说数值（numerical） 线性代数库），并联合调用他们（mix the routine calls to them），即用好函数库不用自己手写：
  1. 用内置运行速度会更快，并且可以有效的利用计算机里可能有的一些并行硬件系统（parallel hardware）
  2. 使用更少的代码实现需要的功能，因此实现的方式更简单，更不容易出错 （be bug free）
• 如果使用了合适的向量化方法（vectorized implementations） ， 代码会简单有效得多，下面举个例子：

2.实例

①简单例子——计算线性回归假设函数

• 计算线性回归假设函数：
  $$\begin{gathered} \begin{array}{rl}{h}_{\theta }(x)& =\sum _{j=0}^n{\theta }_j{x}_j\\ & ={\theta }^{T}x\end{array} \\ \theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ ...\\ {\theta }_n\end{array}\right]x=\left[\begin{array}{c}{x}_0\\ x_1\\ ...\\ x_n\end{array}\right] \end{gathered}$$
• ①Octave 实现：
• 用未向量化（unvectorized implementation） 的代码来计算 h(x) 如下：

prediction = 0.0;
for j = 1:n+1,		% MATLAB中下标从 1 开始，对应上述向量中的从 0 开始
	prediction = prediction + theta(j) * x(j)
end;

• 用向量化（vectorized implementation） 的代码来计算 h(x) 如下：

prediction = theta' * x;

• ②C++实现
• 未向量化：

double prediction = 0.0;
for (int j=0; j<=n; j++)
	prediction += theta[j] * x[j]

• 向量化（使用了 C++ 数值线性代数库）：

double prediction = theta.transpose() * x;

②复杂例子——线性回归梯度下降算法的更新规则

• 梯度下降算法的更新：
  $$\begin{gathered} {\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_j^{(i)} \\ —————————————————— \\ {\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_0^{(i)} \\ {\theta }_1:={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_1^{(i)} \\ {\theta }_2:={\theta }_2-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_2^{(i)} \end{gathered}$$
• 注意：需要同步更新
• 向量化后：
  $$\begin{gathered} \theta :=\theta -\alpha \delta \\ \Downarrow \Downarrow \Downarrow \Downarrow \\ {\mathbb{R}}^{n+1}{\mathbb{R}}^{n+1}{\mathbb{R}}^n{\mathbb{R}}^{n+1} \end{gathered}$$
  其中：
  $$\begin{gathered} \delta =\frac{1}{m}\sum _{i=1}^m\underset{\mathbb{R}}{\underbrace{(h_{\theta }(x^{(i)})-y^{(i)})}}\cdot \underset{{\mathbb{R}}^{n+1}}{\underbrace{x_j^{(i)}}} \\ \delta =\left[\begin{array}{c}{\delta }_0\\ {\delta }_1\\ ...\\ {\delta }_n\end{array}\right]x^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ ...\\ x_n^{(i)}\end{array}\right] \\ {\delta }_0=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_0^{(i)} \end{gathered}$$

总结

• 本文主要介绍了 Octave 的一些基本操作以及对数据的移动、计算、绘制，以及控制语句的实现和向量化的概念。

• 其中基本操作包括基本运算、对变量和矩阵的建立以及使用；移动数据包括计算矩阵的大小以及通过文件来加载数据并对数据进行查找；绘制图像包括单独成像、重合成像和分块成像；除此之外还有控制语句的使用以及函数的定义和使用；最后介绍了一个在实际操作中很有用的思想——向量化的思想，在此基础上合理地运用库函数来实现代码的优化。

• 个人感觉这些不需要都记住，记住常用的就行了，不常用的忘了也可以回来看看