文章目录
Log
2022.01.16开启新的一章
2022.01.17打算明天弄完
2022.01.18今天弄得有点少
2022.01.19还差一些
2022.01.20今天是真弄完了
一、非线性假设(Non-linear hypotheses)
- 为了阐述研究神经网络算法的目的,首先来看几个机器学习的问题作为例子,这几个问题的解决都需要学习复杂的非线性假设。
例一:监督学习分类问题
-
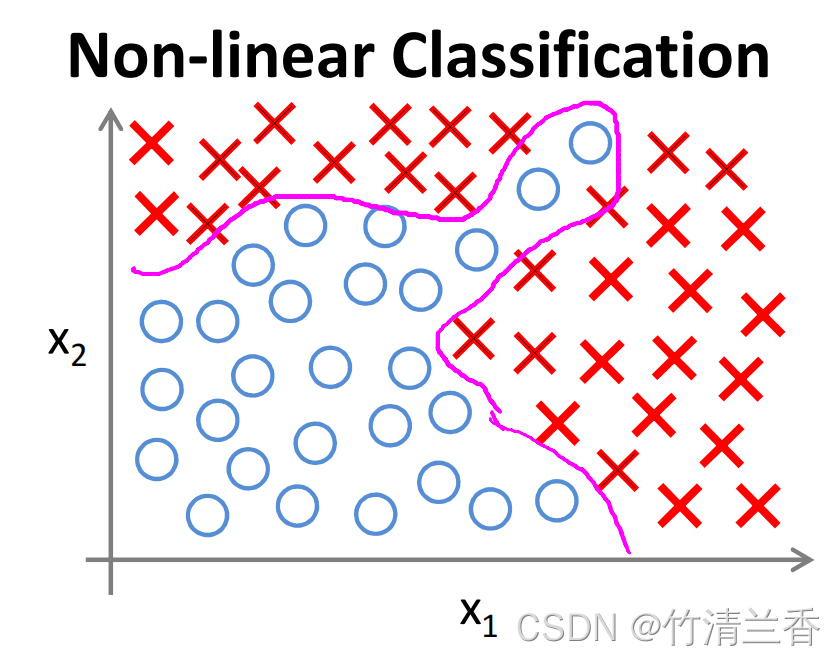
下面是一个监督学习分类问题:
-
利用 logistic 回归来解决这个问题,构造一个包含很多非线性项的 logistic 回归函数:
g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 x 2 + θ 4 x 1 2 x 2 + θ 5 x 1 3 x 2 + θ 6 x 1 x 2 2 + . . . ) g(θ_0+θ_1x_1+θ_2x_2+θ_3x_1x_2+θ_4x_1^2x_2+θ_5x_1^3x_2+θ_6x_1x_2^2+...) g(θ0+θ1x1+θ2x2+θ3x1x2+θ4x12x2+θ5x13x2+θ6x1x22+...) -
此处的 g 仍然是 Sigmoid 函数,其中包含很多多项式,当里面的多项式足够多时,就可以得到能将正负样本分开的假设(上图)。
-
当只有两个特征时,可以将其所有组合都包含到多项式中,因此这种方法能够得到不错的结果。
-
但是一般的机器学习问题往往都有大量的特征,如果要包含所有的二次多项式,那也将是不小的数目。假如只有 100 个特征,那么对应的二次项特征就有 5000 多个:
x 1 2 , x 1 x 2 , x 1 x 3 , x 1 x 4 , . . . , x 1 x 100 x 2 2 , x 2 x 3 , x 2 x 4 , . . . , x 2 x 100 x 100 2 二 次 项 以 O ( n 2 ) 进 行 增 长 三 次 项 以 O ( n 3 ) 进 行 增 长 \begin{aligned} &x_1^2,x_1x_2,x_1x_3,x_1x_4,...,x_1x_{100}\\ &x_2^2,x_2x_3,x_2x_4,...,x_2x_{100}\\ &x_{100}^2\\ &二次项以\ O(n^2)\ 进行增长\\ &三次项以\ O(n^3)\ 进行增长\\ \end{aligned} x12,x1x2,x1x3,x1x4,...,x1x100x22,x2x3,x2x4,...,x2x100x1002二次项以 O(n2) 进行增长三次项以 O(n3) 进行增长 -
项数过多导致结果可能是过拟合的,同时在处理这些项时也存在运算量过大的问题。
-
如果只考虑平方项,忽略组合项的话,虽然最终使用的项数并没有那么多,但是由于忽略的太多会导致得不到想要的结果,对一些特殊的数据不能做出很好的拟合。
-
总结: 当初始特征的个数 n 很大时,将高阶多项式项数包括到特征里,会使特征空间急剧膨胀,当特征个数 n 很大时,则加特征来建立非线性分类器并不是一个好做法。
例二:计算机视觉问题
- 计算机视觉(computer vision)问题: 根据图像的像素点亮度矩阵,来告诉我们这些数值代表一个什么事物。
- 在计算机视觉问题中,使用机器学习算法训练一个分类器来检测图像,来判断图像是否为汽车。
- 用机器学习算法构造一个汽车识别器(car detector) 时,要做的就是提供一个带标签的样本集(一部分是汽车另一部分不是)给识别器进行训练,理想情况下,分类器对于一幅新输入的图片可以判断出是否为一辆汽车。
- 下面论述引入非线性假设的必要性:
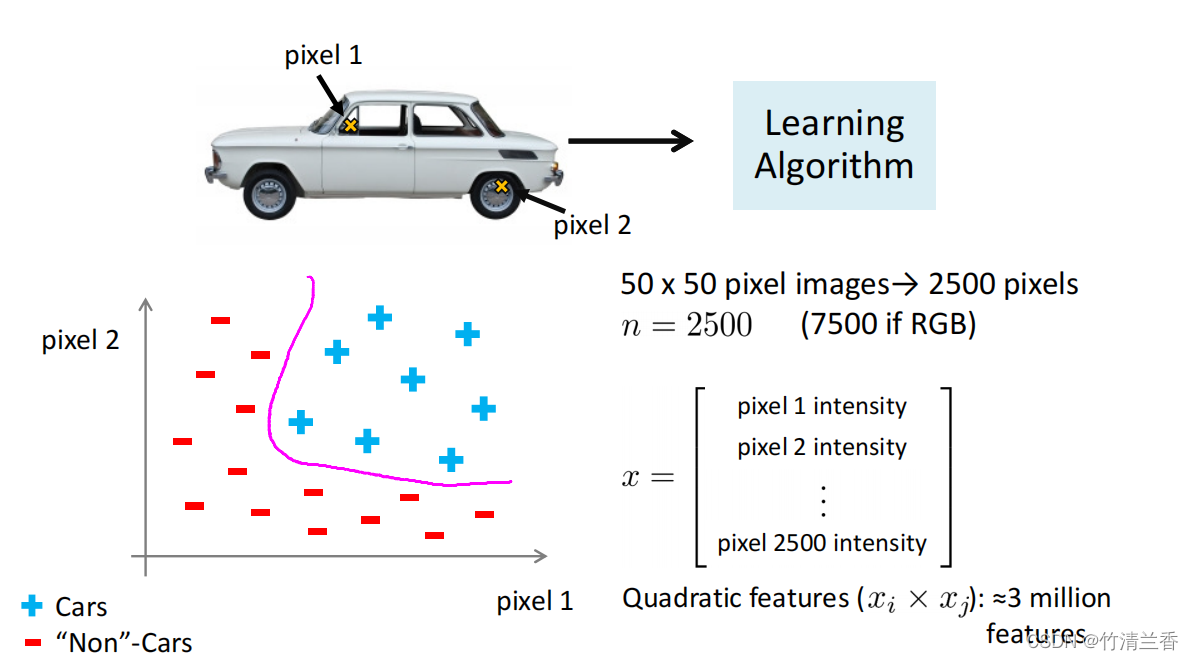
- 从图像中选取两个像素点为例,将这两个像素点的强度作为这张图片的两个特征,体现在下图坐标系中。
- 汽车样本和非汽车样本分布在坐标系中的不同区域,因此需要一个非线性假设来分开这两类样本。
- 假设用 50 × 50 像素的图片,共有 2500个像素点,因此特征向量的元素数量(特征空间的维数) n 就为 2500,特征向量 x 就是包含了所有像素强度的列表(如果存储的是每个像素点的灰度值,那么每个元素的值应该在 0 到 255 之间)。
- 如果使用的是 RGB 彩色图像(每个像素点包含红、绿、蓝三个值)而不是灰度图像,那么 n 就为 7500 (2500*3)。
- 所以如果要通过包含所有二次项特征来学习得到非线性假设,那么按照上图中的公式来计算所有的二次项特征(quadratic features),总共就有约 300 万个特征。如果对于每个样本都要找出并表示 300 万个特征,那成本就太高了。
- 总结: 只是包括平方项或立方项的特征,简单的逻辑回归算法并不是一个在 n 很大时学习复杂的非线性假设的好办法(因为特征过多)。
- 下面将要介绍的神经网络·在学习复杂的非线性假设上·被证明是一种更好的算法(即使输入特征空间或 n 很大)。
二、神经元与大脑(Neurons and the brain)
- 主要内容:一些神经网络的背景知识。
1. 神经网络的起源与实验依据
-
神经网络的起源:人们尝试设计出模仿大脑的算法,上世纪八九十年代神经网络被广泛应用,九十年代的后期应用减少(神经网络的计算量较大),由于计算能力的增加,神经网络在最近再次兴起。
-
一种假设:对于各种各样的问题,大脑处理的方法只需要一个学习算法(one learning algorithm) 就可以了。
-
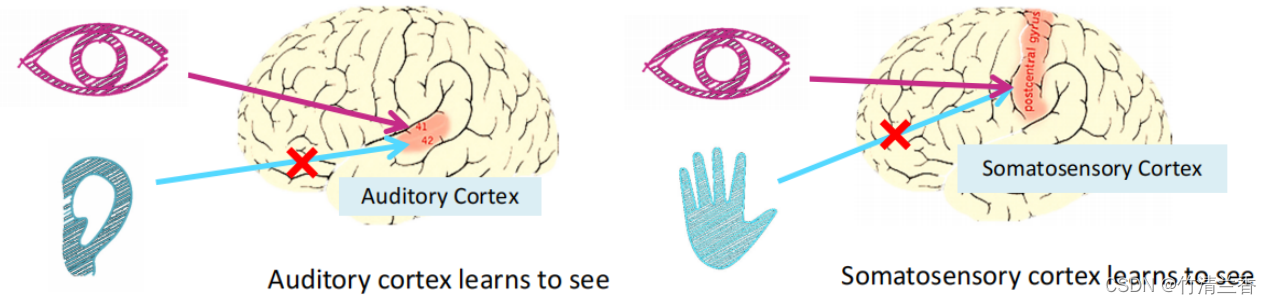
神经重连接(neuro-rewiring)实验: 如下图所示,把动物的耳朵到听觉皮层的神经切断,再将眼睛经由视神经传递的信号传到听觉皮层,那么经过一段时间的训练,该听觉皮层也能学会“看”,即动物可以完成视觉辨别任务。同理也可以对对触觉皮层进行同样的实验。
-
引申出的理念: 如果有一块脑组织可以处理光、声或触觉信号,那么也许存在一种学习算法可以同时处理视觉、听觉和触觉(而不是运行上千个不同的程序),我们就可以找出一种近似实际的大脑学习算法,然后实现它,让大脑自己学习如何处理这些不同类型的数据。
2. 大脑自主学会处理传感器信号的例子
- 大脑有惊人的能力:我们似乎可以把几乎任何一种传感器接入到大脑的几乎任一个部位,大脑就会学会处理它,下面是几个具体的例子:
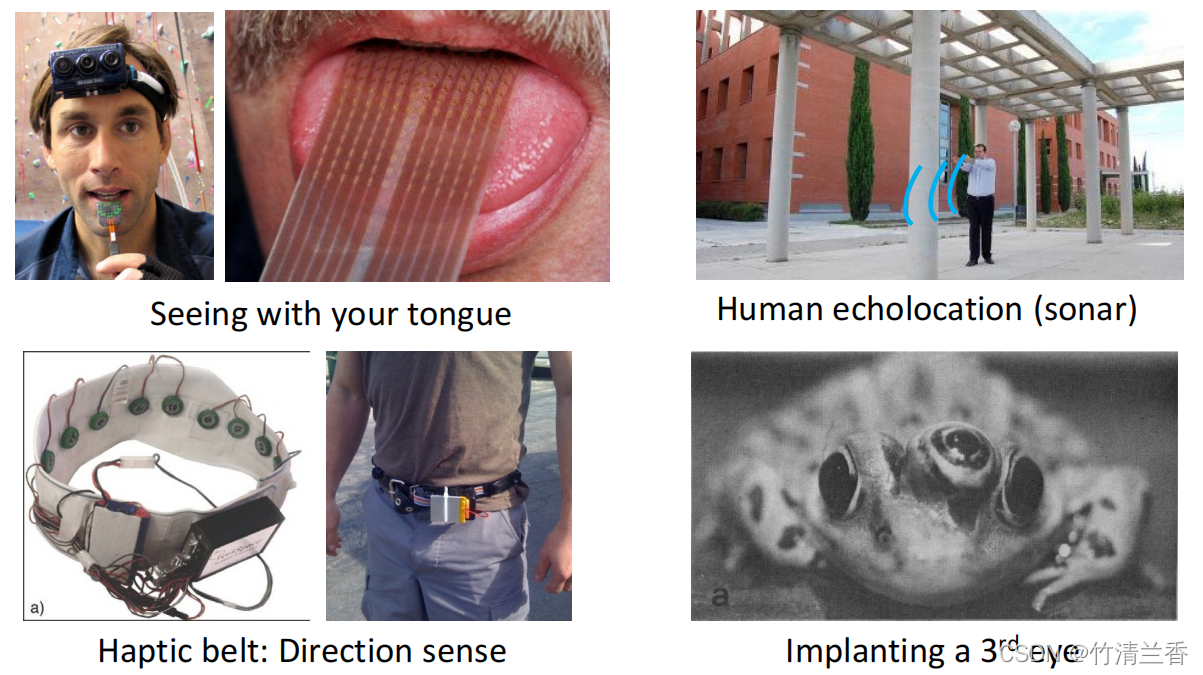
- 用舌头学会看(左上):一个帮助盲人看见世界的 BrainPort 系统,其原理是通过前额的灰度摄像头(grayscale camera) 获取低分辨率的灰度图像,再将信号经导线传递到舌头上安装的电极阵列(array of electrodes) 上,图像中的每一个像素都可以映射到该阵列中,电压的高低代表像素点的明暗。
- 人体回声定位(echolocation)/人体声呐(sonar)(右上):通过弹响指或咂舌头并解读从环境反弹回来的声波模式来感受环境。
- 触觉皮带(Haptic belt)(左下):通过蜂鸣器的震动使人获得方向感。
- 移植第三只眼(右下):移植后青蛙也能学会如何使用第三只眼。
三、模型展示(Model representation)
- 主要内容:如何表示神经网络,即在运用神经网络时我们该如何表示我们的假设或模型
模型一(神经网络的建立)
1. 引入(神经元)
-
由于神经网络模仿了大脑中的神经元或者神经网络,为了解释如何表示假设模型,首先来介绍一下大脑中的单个神经元。
-
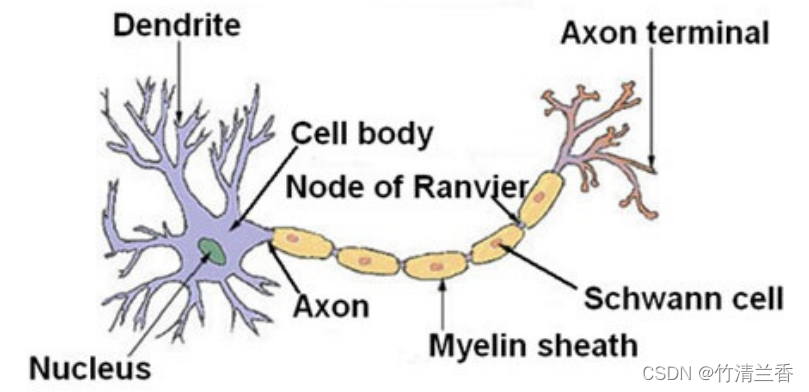
神经元(neuron)(计算单元)主要结构:
- 细胞体——进行计算
- 树突(dendrite)——输入通道
- 轴突(axon)——输出通道
2. 神经网络模型
①单个神经元
-
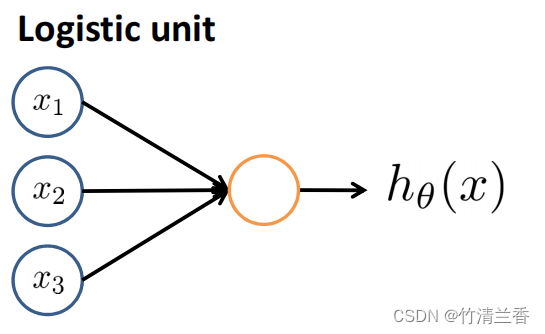
使用一个逻辑单元(logistic unit) 来模拟神经元的工作:
-
上图中,输入信息(篮圈)通过输入通道(左侧黑线)传递给细胞体(黄圈),计算后通过输出通道(右侧黑线)输出计算结果。
-
上图表示对 hθ(x) 进行计算:
h θ ( x ) = 1 1 + e − θ T x x = [ x 0 x 1 x 2 x 3 ] θ = [ θ 0 θ 1 θ 2 θ 3 ] \large{h_θ(x) =\frac{1}{1+e^{-θ^Tx}}}\\\quad\\ x=\left[\begin{matrix} x_0\\ x_1\\ x_2\\ x_3 \end{matrix}\right] \qquadθ=\left[\begin{matrix} θ_0\\ θ_1\\ θ_2\\ θ_3 \end{matrix}\right] hθ(x)=1+e−θTx1x=⎣⎢⎢⎢⎡x0x1x2x3⎦⎥⎥⎥⎤θ=⎣⎢⎢⎢⎡θ0θ1θ2θ3⎦⎥⎥⎥⎤ -
绘制结点时通常只画 x1、x2、x3 ,有必要时会添加一个额外的结点 x0 (数值为 1 ,是否绘制取决于具体例子中能否方便地表示 ),被称作偏置单元(bias unit) 或偏置神经元(bias neuron)。
-
有时也会说上图表示的是一个 Sigmoid 或 logistic 激活函数(Sigmoid / logistic activation function) 的人工神经元(此处的激活函数是指代非线性函数 g(z) 的另一个术语)。
-
θ ,模型的参数(parameter of a model),有时也被称作模型的权重(weights of a model)。
②神经网络
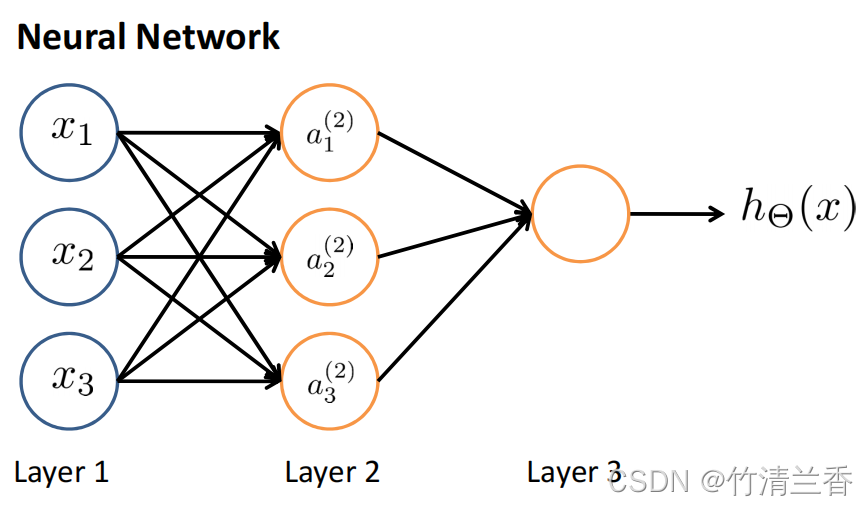
- 神经网络实际上就是一组神经元连接在一起的集合:
- 网络中的第一层(layer 1)也被叫做输入层(input layer),因为我们在这一层输入特征;最后一层(layer 3)叫做输出层(output layer),因为这一层的神经元输出假设的最终计算结果;中间的第二层(layer 2)被称作隐藏层(hidden layer),因为这一层的数据在训练集中是不可见的,一个神经网络中可以有多个隐藏层(该示例中只有一层)。实际上任何非输入层和输出层的层都可以叫做隐藏层。
③神经网络的运算
- 符号解释:
a i ( j ) 第 j 层 第 i 个 神 经 元 ( 或 单 元 ) 的 激 活 项 激 活 项 是 指 由 一 个 具 体 神 经 元 计 算 并 输 出 的 值 Θ ( j ) 权 重 矩 阵 , 控 制 从 第 j 层 到 第 j + 1 层 的 映 射 ( m a p p i n g ) ( t h e t a 大 写 : Θ 小 写 : θ ) \begin{aligned} a^{(j)}_i\qquad\quad &第\ j\ 层第\ i\ 个神经元(或单元)的激活项\\ &激活项是指由一个具体神经元计算并输出的值\\ \Theta^{(j)}\qquad\quad &权重矩阵,控制从第\ j\ 层到第\ j+1\ 层的映射(mapping)\\ &(\ theta\ 大写:\Theta\ 小写:\theta) \end{aligned} ai(j)Θ(j)第 j 层第 i 个神经元(或单元)的激活项激活项是指由一个具体神经元计算并输出的值权重矩阵,控制从第 j 层到第 j+1 层的映射(mapping)( theta 大写:Θ 小写:θ)
- 上图所表示的计算为:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) \begin{aligned} a^{(2)}_1&=g(\Theta^{(1)}_{10}x_0+\Theta^{(1)}_{11}x_1+\Theta^{(1)}_{12}x_2+\Theta^{(1)}_{13}x_3)\\ a^{(2)}_2&=g(\Theta^{(1)}_{20}x_0+\Theta^{(1)}_{21}x_1+\Theta^{(1)}_{22}x_2+\Theta^{(1)}_{23}x_3)\\ a^{(2)}_3&=g(\Theta^{(1)}_{30}x_0+\Theta^{(1)}_{31}x_1+\Theta^{(1)}_{32}x_2+\Theta^{(1)}_{33}x_3)\\ h_\Theta(x)&=a^{(3)}_1=g(\Theta^{(2)}_{10}a_0^{(2)}+\Theta^{(2)}_{11}a_1^{(2)}+\Theta^{(2)}_{12}a_2^{(2)}+\Theta^{(2)}_{13}a_3^{(2)})\\ \end{aligned} a1(2)a2(2)a3(2)hΘ(x)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2)) - 第一个隐藏单元 a1(2) 的激活值为等式后面 Sigmoid 函数的函数值
- Θ(1) 就是控制着从三个输入单元到三个隐藏单元的映射的参数矩阵(是一个 3×4 的矩阵)
- 一般地,如果一个网络在第 j 层有 s j 个单元,第 j+1 层有 s j+1 个单元,那么矩阵Θ(j) 就是控制第 j 层到第 j+1 层的的映射的矩阵,它的维度为 s j+1×(s j + 1)
模型二(神经网络的工作原理)
- 主要内容:如何高效进行计算,展示一个向量化的实现方法,以及为什么这样是表示神经网络的好方法,并且明白他们如何帮助我们学习复杂的非线性假设函数。
1. 前向传播(forward propagation):向量化操作
- 仍然用上面的例子,通过之前的方程可以计算出三个隐藏单元的激活值,然后利用这些值来计算最终输出假设函数 h(x) ,下面定义一些额外的项:
z 1 ( 2 ) = Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 z 2 ( 2 ) = Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 z 3 ( 2 ) = Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 \begin{aligned} z^{(2)}_1&=\Theta^{(1)}_{10}x_0+\Theta^{(1)}_{11}x_1+\Theta^{(1)}_{12}x_2+\Theta^{(1)}_{13}x_3\\ z^{(2)}_2&=\Theta^{(1)}_{20}x_0+\Theta^{(1)}_{21}x_1+\Theta^{(1)}_{22}x_2+\Theta^{(1)}_{23}x_3\\ z^{(2)}_3&=\Theta^{(1)}_{30}x_0+\Theta^{(1)}_{31}x_1+\Theta^{(1)}_{32}x_2+\Theta^{(1)}_{33}x_3\\ \end{aligned} z1(2)z2(2)z3(2)=Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3=Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3=Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3 - z 的上标 (2) 表示这些值和第二层(隐藏层)有关,这些 z 值都是线性组合某个特定的神经元的输入值 x0、x1、x2、x3的加权线性组合(weighted linear combination)。通过下面的式子来实现向量化:
x = [ x 0 x 1 x 2 x 3 ] z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] z ( 2 ) = Θ ( 1 ) x a ( 2 ) = g ( z ( 2 ) ) z ( 2 ) 、 a ( 2 ) ∈ R 3 \begin{aligned} x=&\left[\begin{matrix} x_0\\ x_1\\ x_2\\ x_3 \end{matrix}\right] \qquad z^{(2)}=\left[\begin{matrix} z^{(2)}_1\\ z^{(2)}_2\\ z^{(2)}_3 \end{matrix}\right]\\\quad\\ z^{(2)}&=\Theta^{(1)}x\\ a^{(2)}&=g(z^{(2)})\\\ \\ z^{(2)}&、\ a^{(2)}\in \R^3 \end{aligned} x=z(2)a(2) z(2)⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤z(2)=⎣⎢⎡z1(2)z2(2)z3(2)⎦⎥⎤=Θ(1)x=g(z(2))、 a(2)∈R3 - 为了后续的符号统一,将第一层输入层 x 记为 a(1),进一步得到:
z ( 2 ) = Θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) \begin{aligned} z^{(2)}&=\Theta^{(1)}a^{(1)}\\ a^{(2)}&=g(z^{(2)})\\\ \\ \end{aligned} z(2)a(2) =Θ(1)a(1)=g(z(2)) - 为了注意额外的偏置单元接下来要加上:
Add a 0 ( 2 ) = 1 ⇒ a ( i ) ∈ R 4 \textbf{Add}\ a^{(2)}_0=1\ \ \Rightarrow\ \ a^{(i)}\in \R^4 Add a0(2)=1 ⇒ a(i)∈R4 - 为了计算假设函数的实际输出值,只需计算:
z ( 3 ) = Θ ( 2 ) a ( 2 ) h Θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) z^{(3)}=\Theta^{(2)}a^{(2)}\\ h_\Theta(x)=a^{(3)}=g(z^{(3)}) z(3)=Θ(2)a(2)hΘ(x)=a(3)=g(z(3)) - 以上计算 h(x) 的过程被称为前向传播(forward propagation),这样命名是因为我们是从输入单元的激活项开始,然后进行前项传播给隐藏层,计算隐藏层的激活项,然后继续向前传播,并计算输出层的激活项。
- 上面的过程是前向传播的向量化实现方法。
2. 通过前向传播理解神经网络的作用
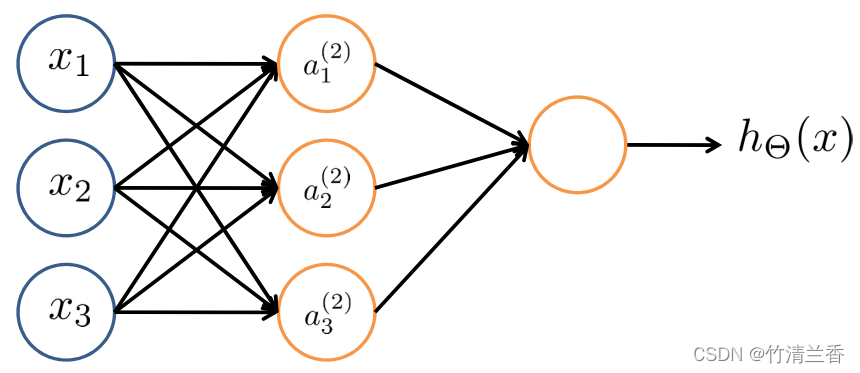
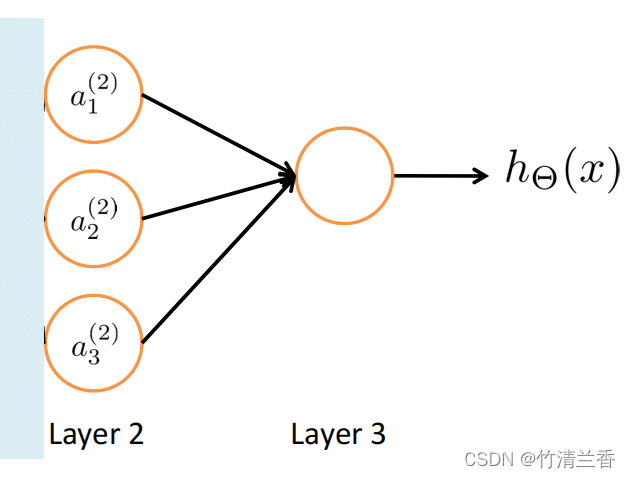
- 先不看输入层看剩余的部分:
- 可以得到以下式子:
h Θ ( x ) = g ( Θ 1 0 ( 2 ) a 0 ( 2 ) + Θ 1 1 ( 2 ) a 1 ( 2 ) + Θ 1 2 ( 2 ) a 2 ( 2 ) + Θ 1 3 ( 2 ) a 3 ( 2 ) ) h_\Theta(x)=g(\Theta^{\red{(2)}}_{\red{1}0}a^{\red{(2)}}_{0}+\Theta^{\red{(2)}}_{\red{1}1}a^{\red{(2)}}_{1}+\Theta^{\red{(2)}}_{\red{1}2}a^{\red{(2)}}_{2}+\Theta^{\red{(2)}}_{\red{1}3}a^{\red{(2)}}_{3}) hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2)) - 忽略式子中标红的部分,剩下的内容除了 theta 大写外就是标准的逻辑回归模型(实际上就是在做逻辑回归的内容),只是输入逻辑回归的特征是通过隐藏层计算的这些数值。
- 换句话说,神经网络所做的就像是逻辑回归,只是输入特征不是直接用原来的 x1、x2、x3,而是用 a1、a2、a3 作为新的特征。
- 而这些 a 是学习得到的函数输入值(they are learned as function of the input),就是从第一层映射到第二层的函数,该函数由其他参数 Θ(1) 决定。
- 根据为 Θ 选择的不同参数,有时可以学习到一些很有趣和复杂的特征,进一步就可以得到一个更好的假设函数(比使用原始输入的更好,也可以使用多项式作为输入项,这个算法可以灵活地尝试快速学习任意的特征项)。
3. 其他类型的神经网络表示方法
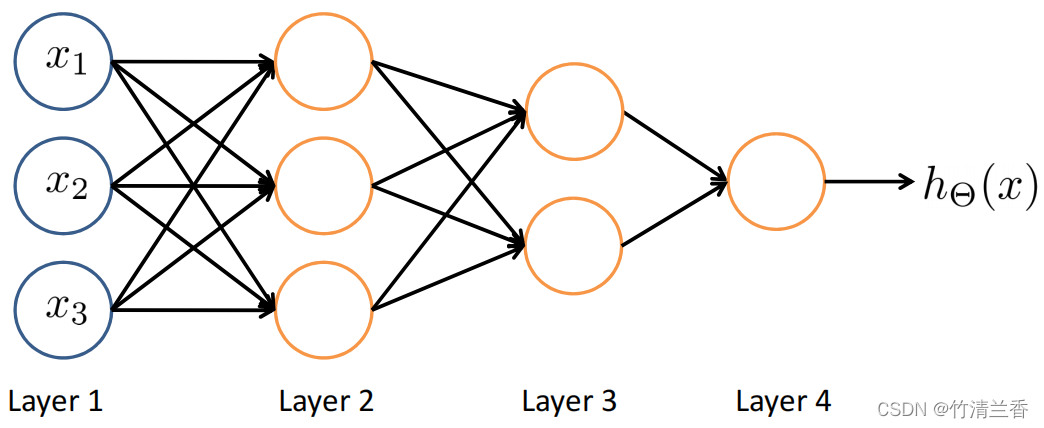
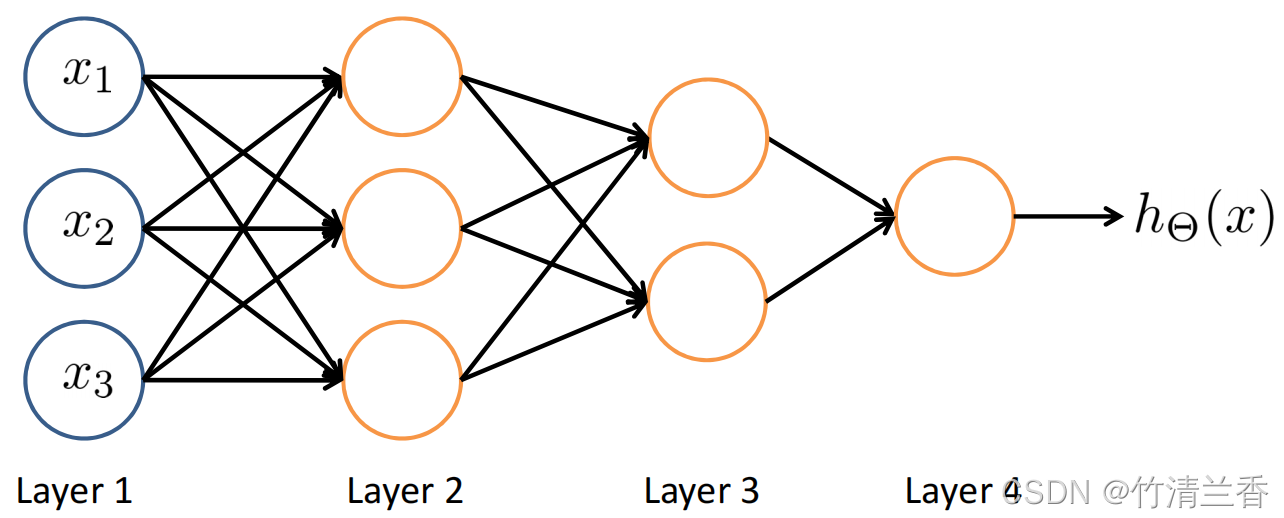
- 可以使用以下的图来表示神经网络:
- 神经网络中神经元的连接方式被称为神经网络的架构(the architecture)(架构指不同的神经元的连接方式)。
- 简单描述一下上图,从输入层(layer 1)输入特征,第一个隐藏层(layer 2)可以计算输入层的复杂功能,第二个隐藏层(layer 3)可以将第二层训练出的特征项作为输入,然后再第三层计算出更复杂的特征。当到达输出层(layer 4)时,就可以利用在第三层训练出的更复杂的特征作为输入,以此得到非常有趣的非线性假设函数
四、例子与直觉理解(Examples and intuitions)
- 主要内容:通过一个详细的例子来说明神经网络是怎样计算复杂非线性假设函数的输入的。
非线性分类实例:异或非(XNOR)
-
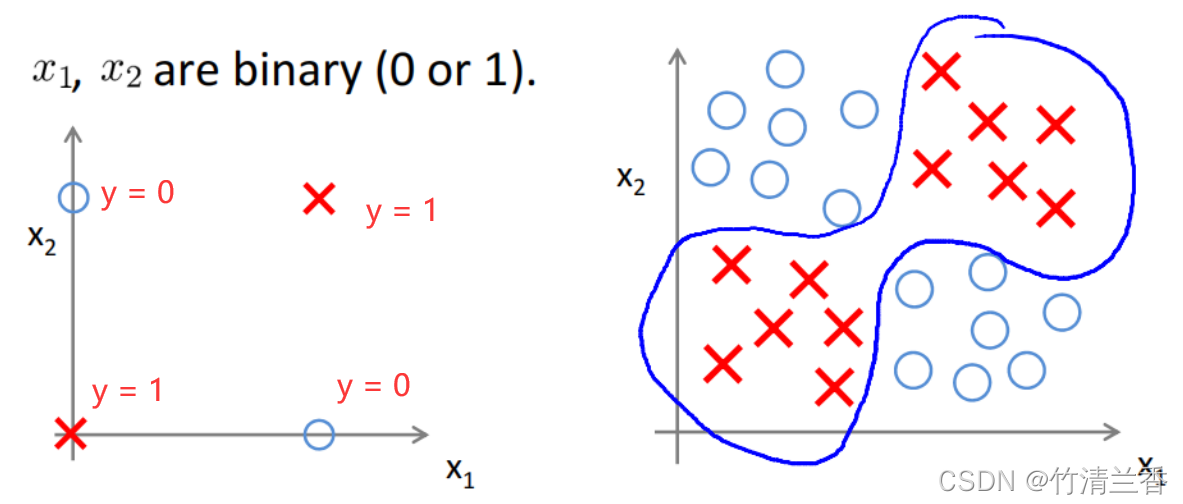
有 x1 和 x2 两个输入特征,均为二进制(只能为 0 或 1)。
-
下图左只画了两个正样本和两个负样本,但是可以看做事复杂的机器学习问题的一个简化版本(下图右),想要做的就是学习一个非线性的判断边界来区分这些正样本和负样本,用左边的例子来简单的说明如何用神经网络来实现。
-
需要计算的目标函数为:
y = x 1 X O R x 2 x 1 X N O R ⏟ N O T ( x 1 X O R x 2 ) x 2 \begin{aligned} y\ =\ &x_1\ XOR\ x_2\\ &x_1\ \underbrace{XNOR}_{NOT(x_1\ XOR\ x_2)}\ x_2 \end{aligned} y = x1 XOR x2x1 NOT(x1 XOR x2) XNOR x2 -
即当正样本同时为真或同时为假时 y 的值才为 1(如果 y = 0 则代表有且只有一个为真)。
-
可以通过构建一个神经网络来拟合这样的训练集。为了拟合 XNOR 运算的神经网络,首先先从简单的 AND 运算的网络入手:
1. 逻辑与(AND)
-
输入变量:x1、x2 ∈ {0, 1}
-
目标函数:y = x1 AND x2
-
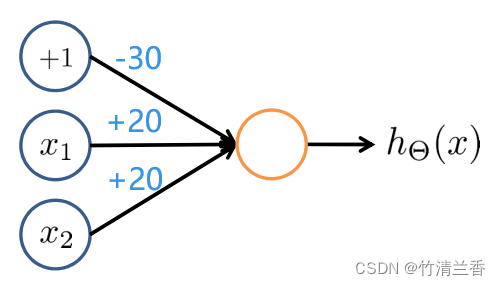
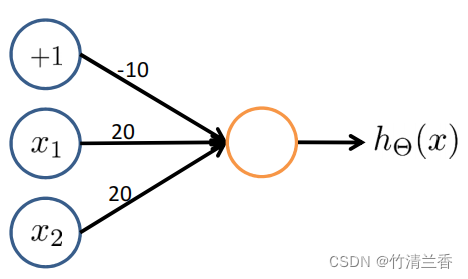
通过添加一个偏置单元(也称 +1 单元)来得到只含单个神经元的网络,进而计算 AND 函数。
-
随后添加每个参数的权重,进一步得到下式:
h Θ ( x ) = g ( − 30 ⏟ Θ 10 ( 1 ) + 20 ⏟ Θ 11 ( 1 ) x 1 + 20 ⏟ Θ 12 ( 1 ) x 2 ) h_\Theta(x)=g(\underbrace{-30}_{\Theta^{(1)}_{10}}+\underbrace{20}_{\Theta^{(1)}_{11}}x_1+\underbrace{20}_{\Theta^{(1)}_{12}}x_2) hΘ(x)=g(Θ10(1) −30+Θ11(1) 20x1+Θ12(1) 20x2) -
将所有可能的取值代入式子中,可以得到以下真值表:
| x1 | x2 | hΘ(x) | x1 AND x2 |
|---|---|---|---|
| 0 | 0 | g(-30) ≈ 0 | 0 |
| 0 | 1 | g(-10) ≈ 0 | 0 |
| 1 | 0 | g(-10) ≈ 0 | 0 |
| 1 | 1 | g( 10) ≈ 1 | 1 |
- 可以发现,函数的计算结果是逻辑与的计算结果,即:hΘ(x) ≈ x1 AND x2
- 通过真值表,我们就可以知道神经网络计算的逻辑函数的取值是怎样的
2. 逻辑或(OR)
h
Θ
(
x
)
=
g
(
−
10
+
20
x
1
+
20
x
2
)
h_\Theta(x)=g({-10}+{20}x_1+{20}x_2)
hΘ(x)=g(−10+20x1+20x2)
| x1 | x2 | hΘ(x) | x1 OR x2 |
|---|---|---|---|
| 0 | 0 | g(-10) ≈ 0 | 0 |
| 0 | 1 | g( 10) ≈ 1 | 1 |
| 1 | 0 | g( 10) ≈ 1 | 1 |
| 1 | 1 | g( 30) ≈ 1 | 1 |
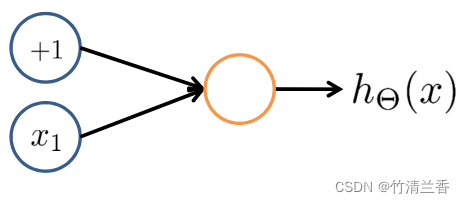
3. 逻辑非(NOT - Negation)
h
Θ
(
x
)
=
g
(
10
+
−
20
x
1
)
h_\Theta(x)=g({10}+{-20}x_1)
hΘ(x)=g(10+−20x1)
| x1 | hΘ(x) | NOT x1 |
|---|---|---|
| 0 | g( 10) ≈ 1 | 1 |
| 1 | g(-10) ≈ 0 | 0 |
- 主要思想:在预期得到非结果的变量前放一个很大的权重。
- 思考如何做:(NOT x1) AND (NOT x2)
- 提示:当两个变量均为 0 时,表达式的值为 1。
4. 异或非(XNOR)
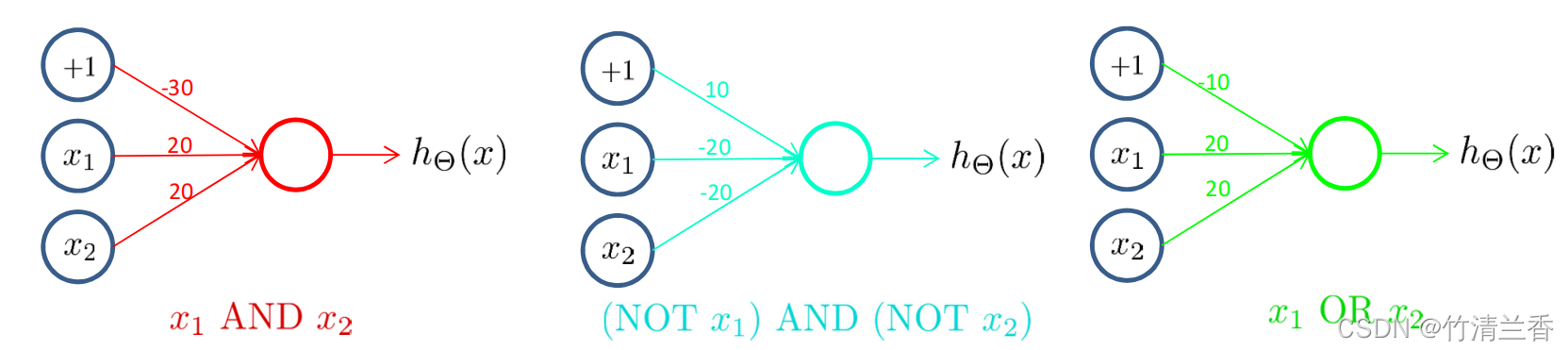
- 将以下三部分组合到一起就能得到 x1 XNOR x2:
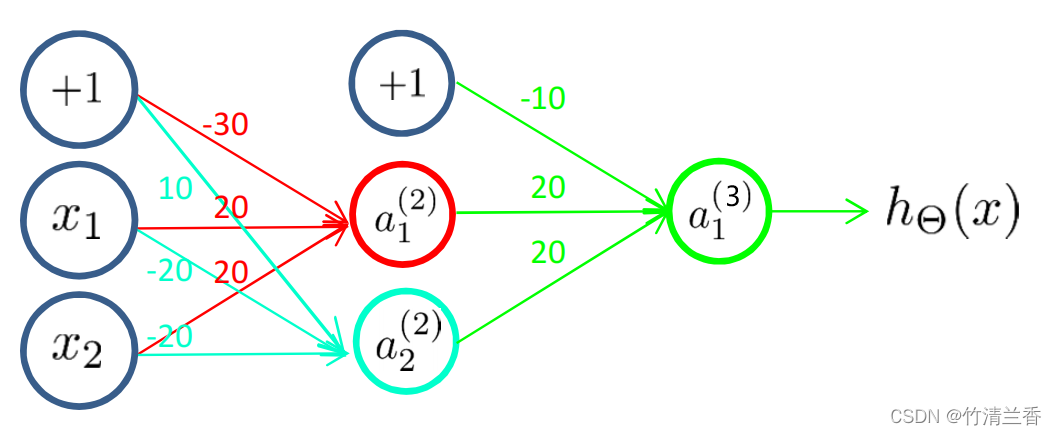
- 组合后的神经网络图:
- 得到对应的真值表:
| x1 | x2 | a1(2) | a2(2) | hΘ(x) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
- 该神经网络有一个输入层,一个隐藏层以及一个输出层。最后会得到一个非线性的决策边界,用以计算 XNOR 函数。换句话说,输入都放在输入层然后在中间放一个隐藏层,用来计算一些关于输入的略微复杂的功能;然后再继续增加一层用于计算一个更复杂的非线性函数。
- 就像上图一样,神经网络可以计算复杂的函数。当网络拥有许多层时,在第二层中有一些关于输入的相对简单的函数,第三层又在此基础上计算更加复杂的方程,在往后一层计算的函数就越来越复杂。
实例:数字识别
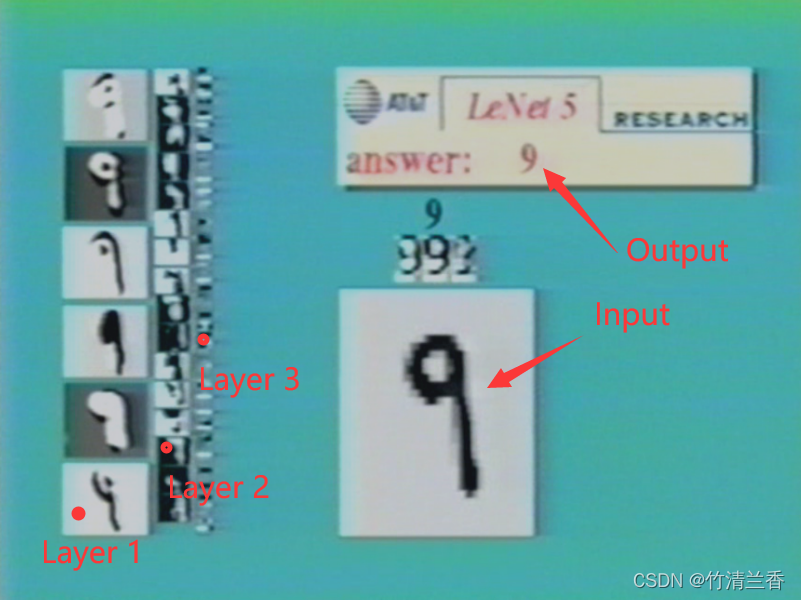
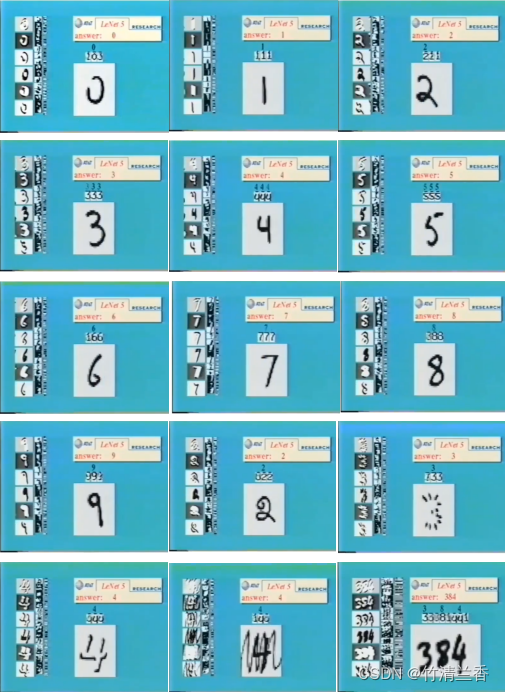
- 神经网络的早期成果之一就是用来识别邮政编码,帮助识别人手写的邮编来实现自助寄件。
- 输入的图像(原始的像素点)通过第一个隐藏层计算出一系列特征,再通过下一个隐藏层计算出更复杂的特征,然后再往下再复杂,最后这些特征被用于逻辑回归分类器的最后一层,来准确地预测出神经网络所看到的数字。
五、多元分类(Multi-class classification)
- 主要内容:利用神经网络解决多类别分类问题。
- 上一部分提到的手写数字识别就是一个多类别分类问题,即从 0 到 9 共十个数字对应十个类别。
一对多法的拓展
- 要在神经网络中实现多类别分类采用的方法本质上是一对多法的拓展。
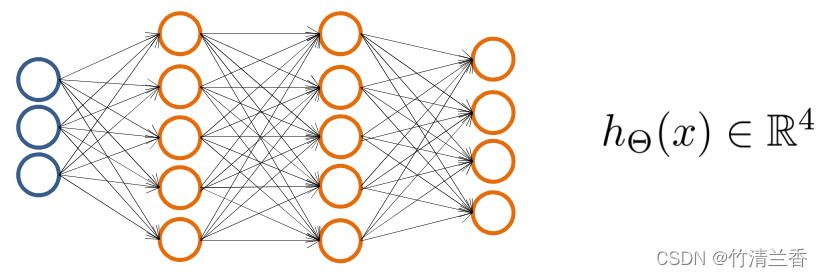
- 假设有一个计算机视觉的例子,需要识别四个类别的对象:行人、汽车、摩托车、货车
- 建立一个有四个输出单元的神经网格,输出将是一个含四个数的向量(四维向量),用第一个单元判断是否是行人,以此类推。
W a n t h Θ ≈ [ 1 0 0 0 ] ⏟ w h e n p e d e s t r i a n h Θ ≈ [ 0 1 0 0 ] ⏟ w h e n c a r h Θ ≈ [ 0 0 1 0 ] ⏟ w h e n m o t o r c y c l e h Θ ≈ [ 0 0 0 1 ] ⏟ w h e n t r u c k T r a i n i n g s e t : ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) y ( i ) o n e o f p e d e s t r i a n [ 1 0 0 0 ] 、 c a r [ 0 1 0 0 ] 、 m o t o r c y c l e [ 0 0 1 0 ] 、 t r u c k [ 0 0 0 1 ] \begin{aligned} &Want\ \ \underbrace{h_\Theta≈ \left[\begin{matrix} 1\\ 0\\ 0\\ 0 \end{matrix}\right]}_{when\ pedestrian} \ \ \underbrace{h_\Theta≈ \left[\begin{matrix} 0\\ 1\\ 0\\ 0 \end{matrix}\right]}_{when\ car} \ \ \underbrace{h_\Theta≈ \left[\begin{matrix} 0\\ 0\\ 1\\ 0 \end{matrix}\right]}_{when\ motorcycle} \ \ \underbrace{h_\Theta≈ \left[\begin{matrix} 0\\ 0\\ 0\\ 1 \end{matrix}\right]}_{when\ truck}\\\ \\ &Training\ \ set:\ \ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\\\ \\ &y^{(i)}\ \ one \ of\ \ _ {pedestrian}^{\left[\begin{matrix} 1\\ 0\\ 0\\ 0 \end{matrix}\right]}、_ {car}^{\left[\begin{matrix} 0\\ 1\\ 0\\ 0 \end{matrix}\right]}、_ {motorcycle}^{\left[\begin{matrix} 0\\ 0\\ 1\\ 0 \end{matrix}\right]}、_ {truck}^{\left[\begin{matrix} 0\\ 0\\ 0\\ 1 \end{matrix}\right]} \end{aligned} Want when pedestrian hΘ≈⎣⎢⎢⎡1000⎦⎥⎥⎤ when car hΘ≈⎣⎢⎢⎡0100⎦⎥⎥⎤ when motorcycle hΘ≈⎣⎢⎢⎡0010⎦⎥⎥⎤ when truck hΘ≈⎣⎢⎢⎡0001⎦⎥⎥⎤Training set: (x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))y(i) one of pedestrian⎣⎡1000⎦⎤、car⎣⎡0100⎦⎤、motorcycle⎣⎡0010⎦⎤、truck⎣⎡0001⎦⎤
总结
- 本文主要介绍了神经网络的相关内容,包括起源、模型的建立、工作原理以及几个直观的实例。
- 当一个问题中的特征数过多时,一般采用神经网络来进行拟合计算,而不是通过增加特征来来建立非线性分类器。
- 神经网络最初是为了模拟人类大脑而建立的,希望可以实现只通过一个算法对不同类型的数据进行处理(学这里的时候感觉大脑好神奇,一个特定的区域只要经过一段时间的学习就可以处理其他类型的信号)。
- 在神经网络模型的建立中,首先通过逻辑单元来模拟神经元的工作,不同的神经元连接在一起后可以形成神经网络,包含一个输入层,一个输出层和至少一个隐藏层。
- 神经网络的工作原理实际上就是前向传播,即从输入特征后逐层计算到输出结果(依次从输入层到隐藏层再到输出层计算激活项的过程),该过程可以通过向量化的操作实现。
- 在具体例子中,通过建立逻辑与、逻辑或、逻辑非的神经元,再将其进行组合得到了可以表示异或非的神经网络;除此之外,神经网络还可以解决多元分类问题,比如手写数字识别、计算机视觉对行人汽车等多类对象进行区分,它实际上是一对多方法的拓展。