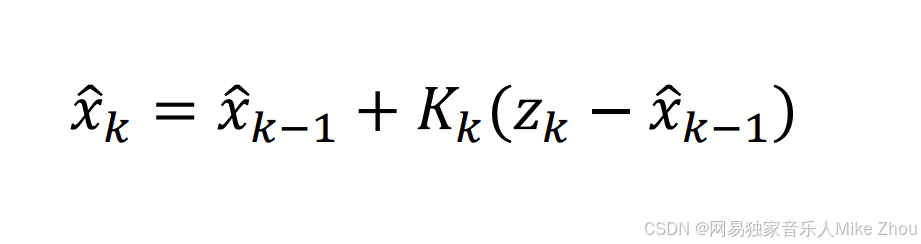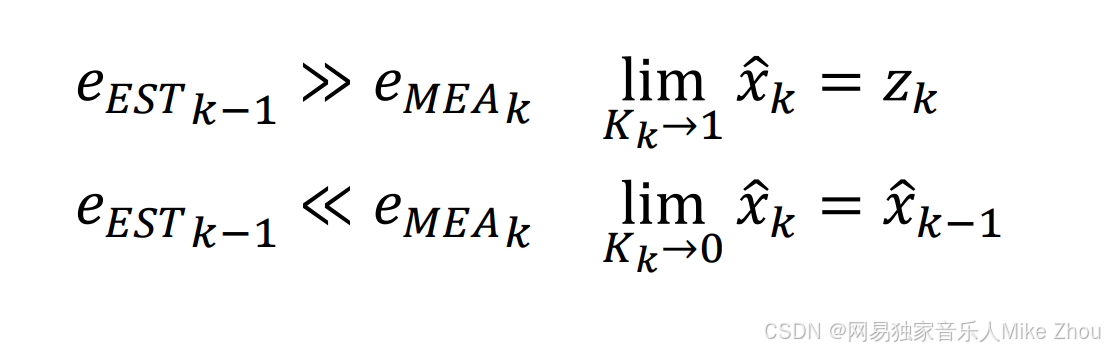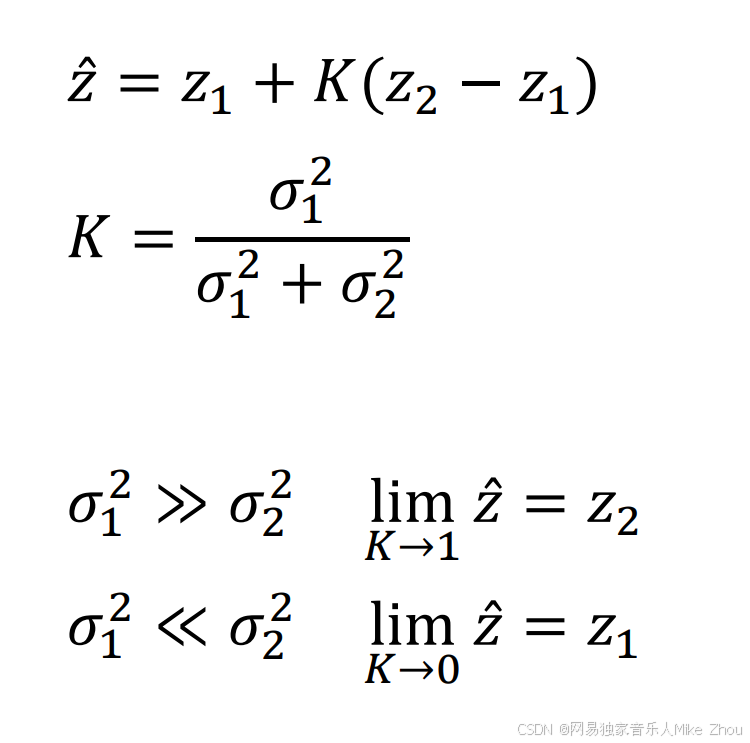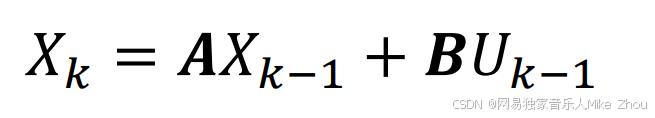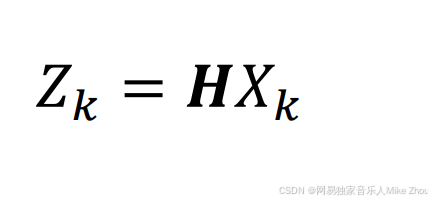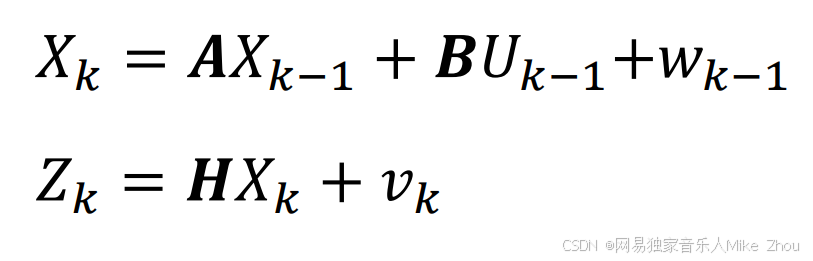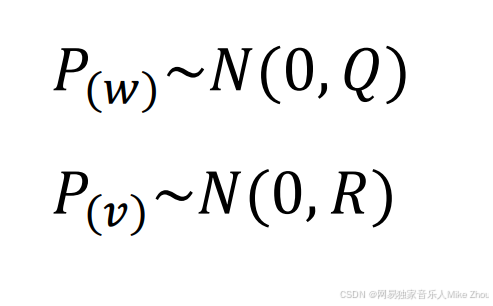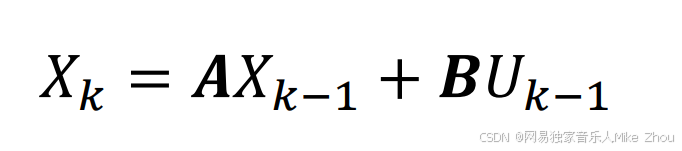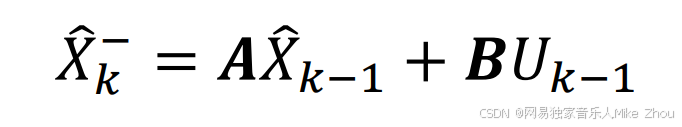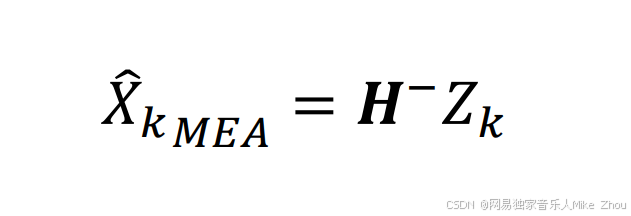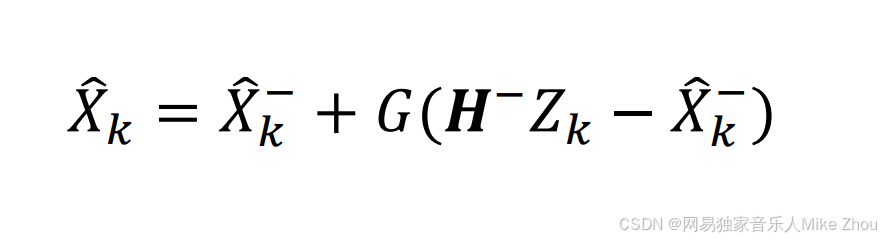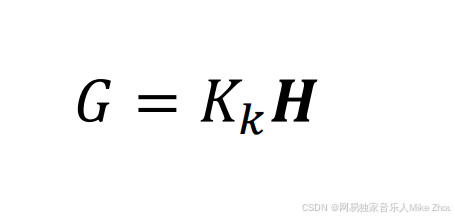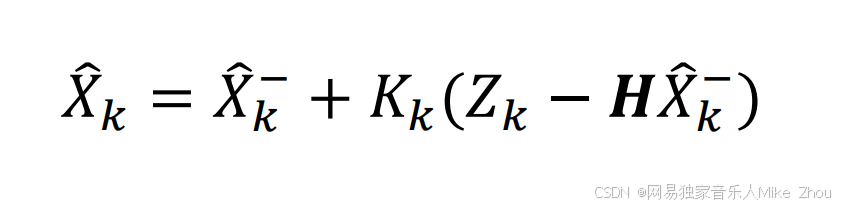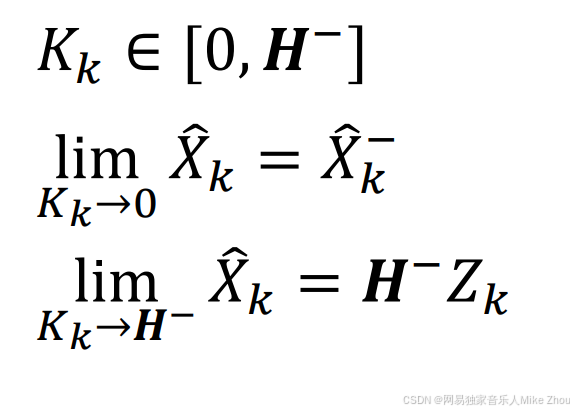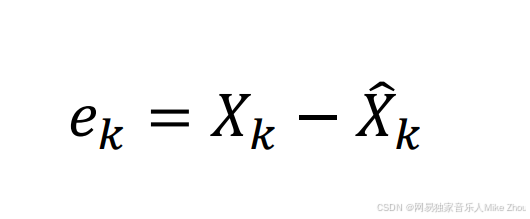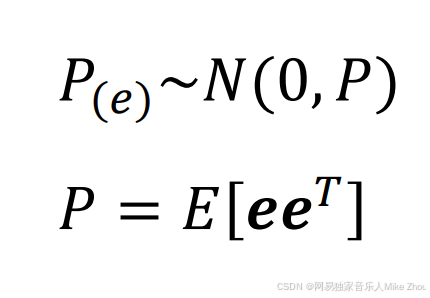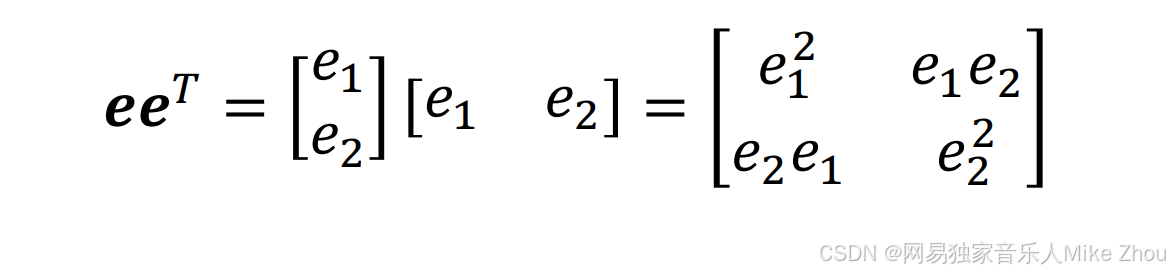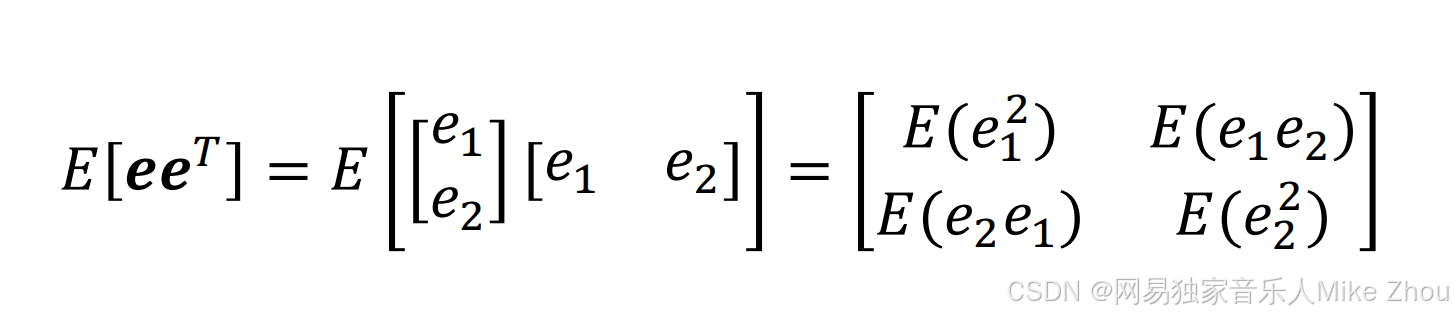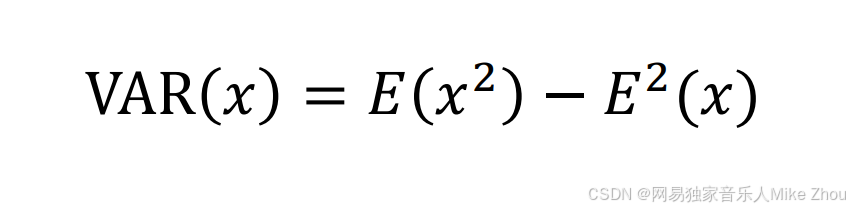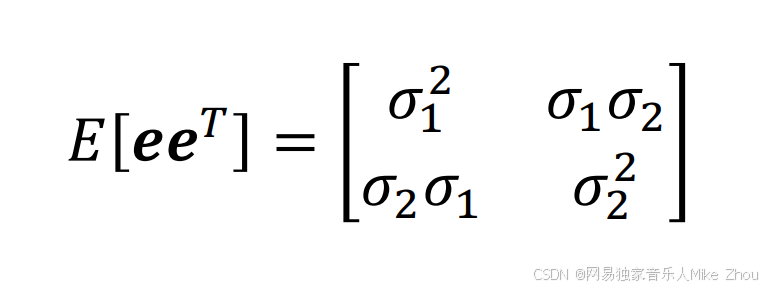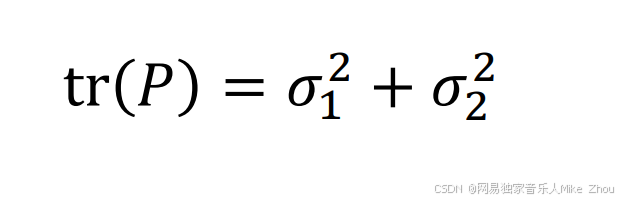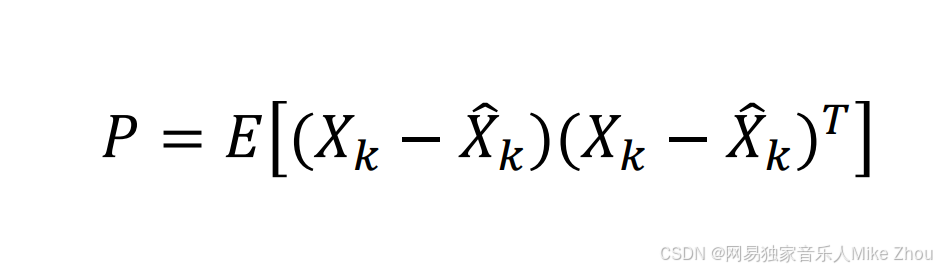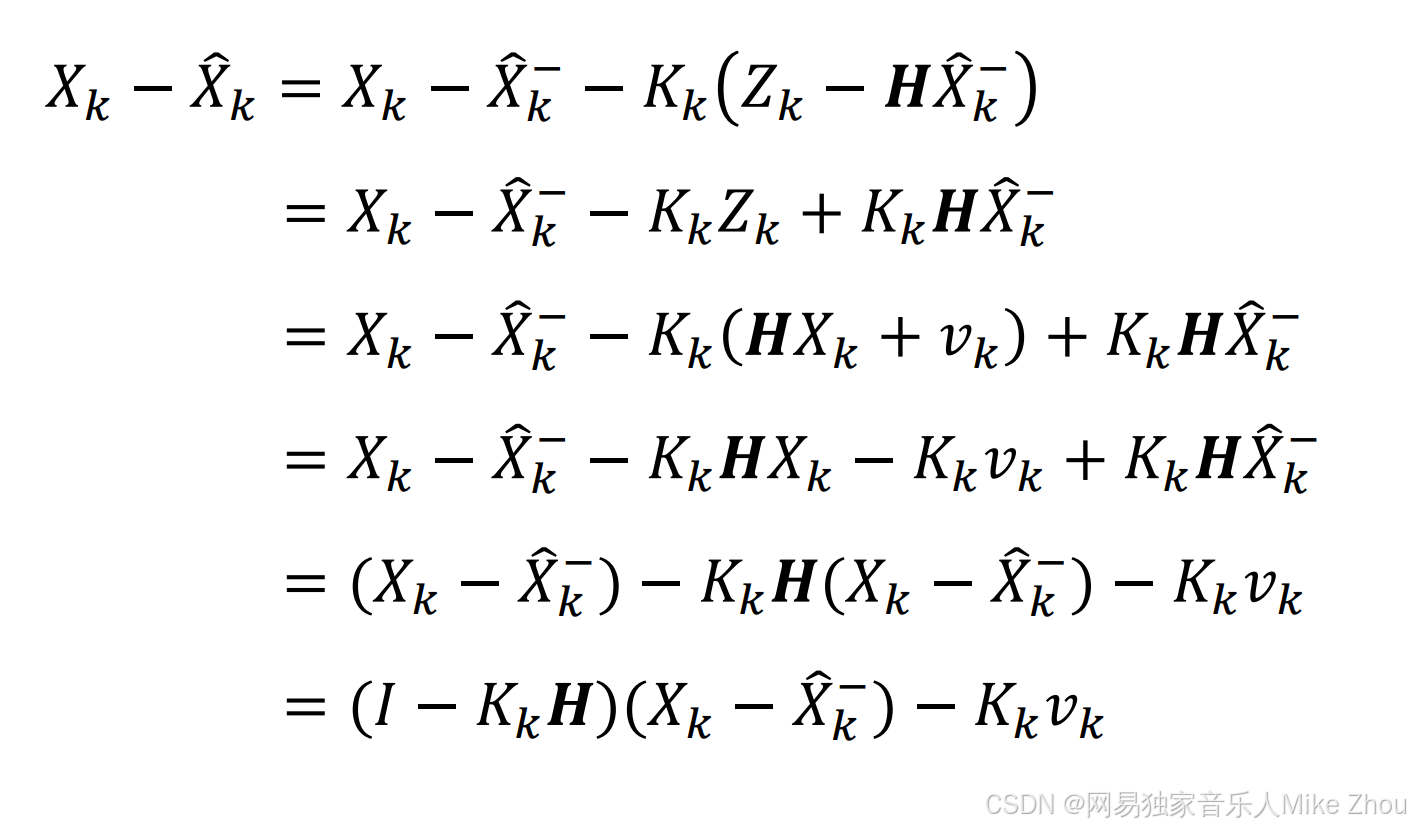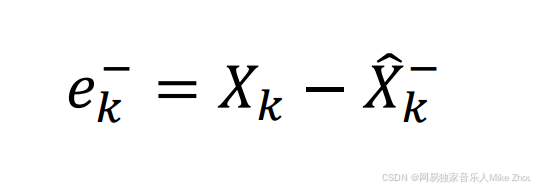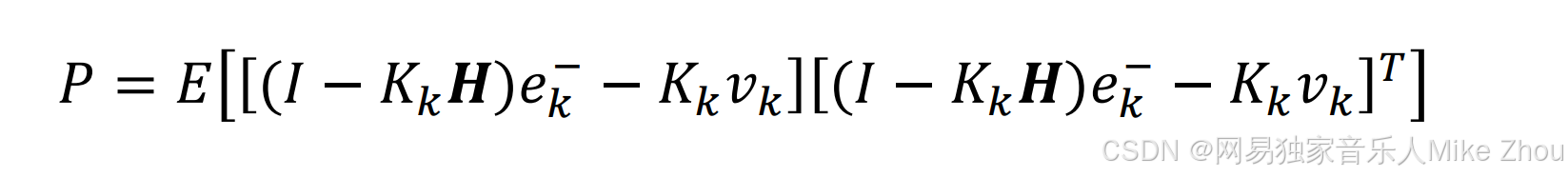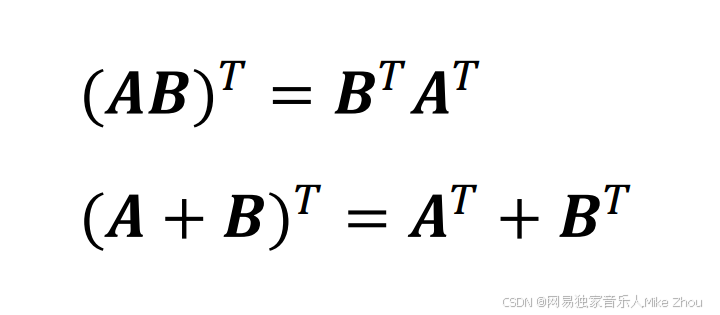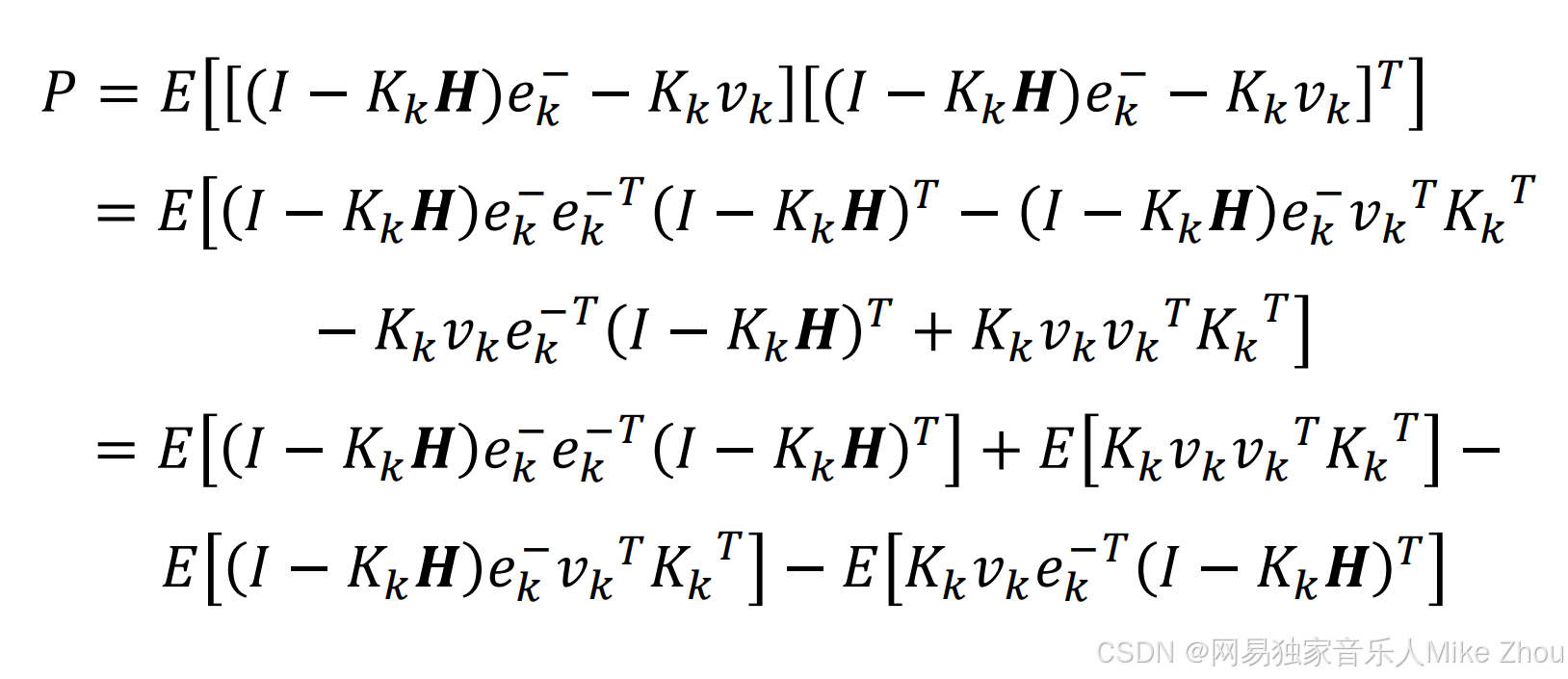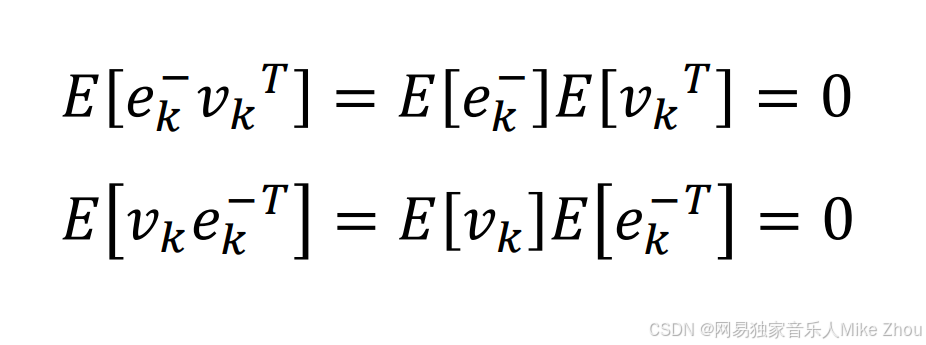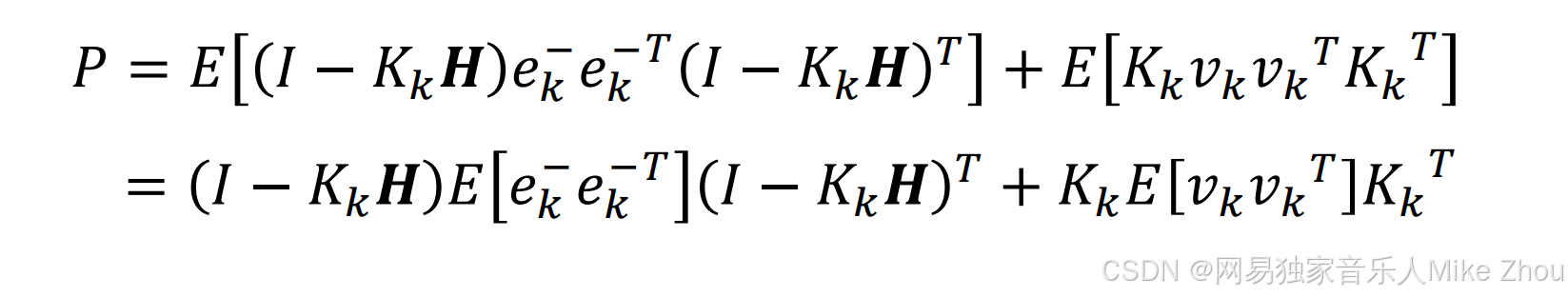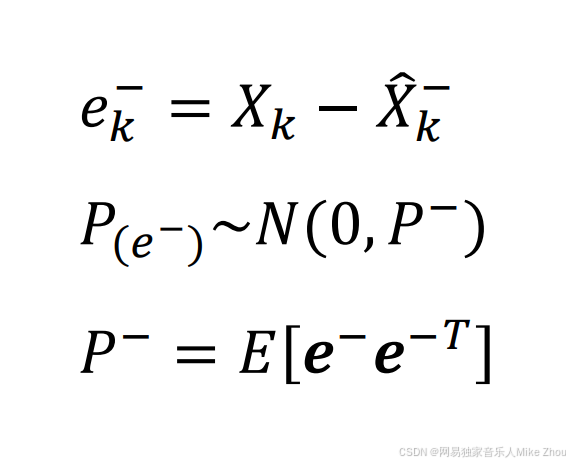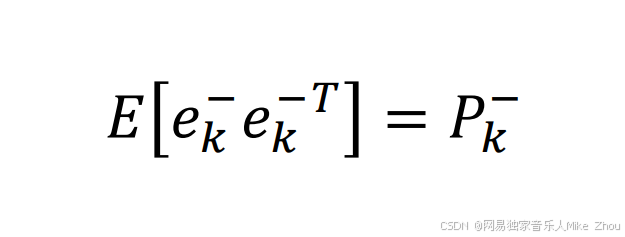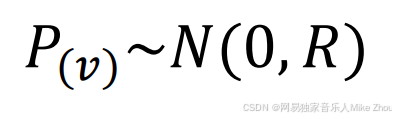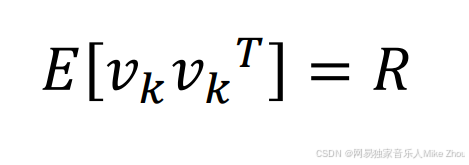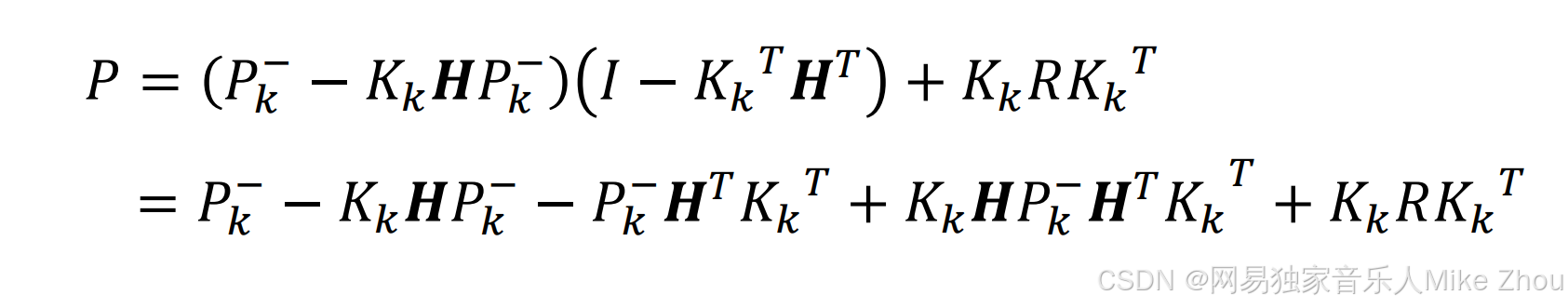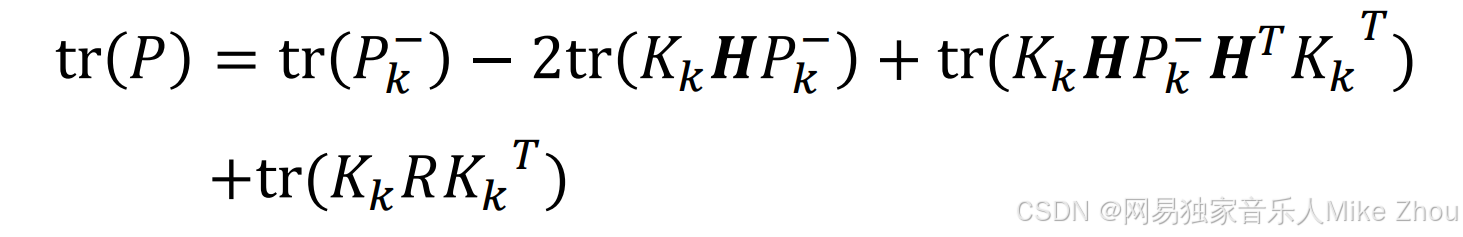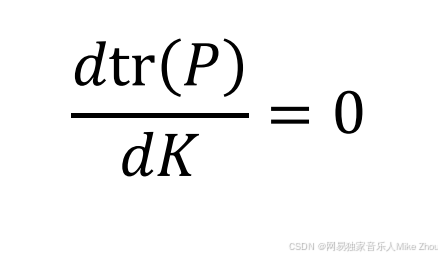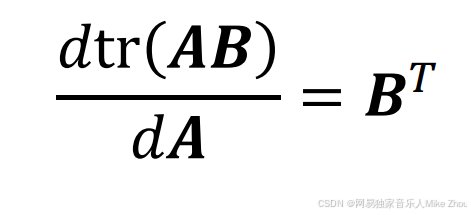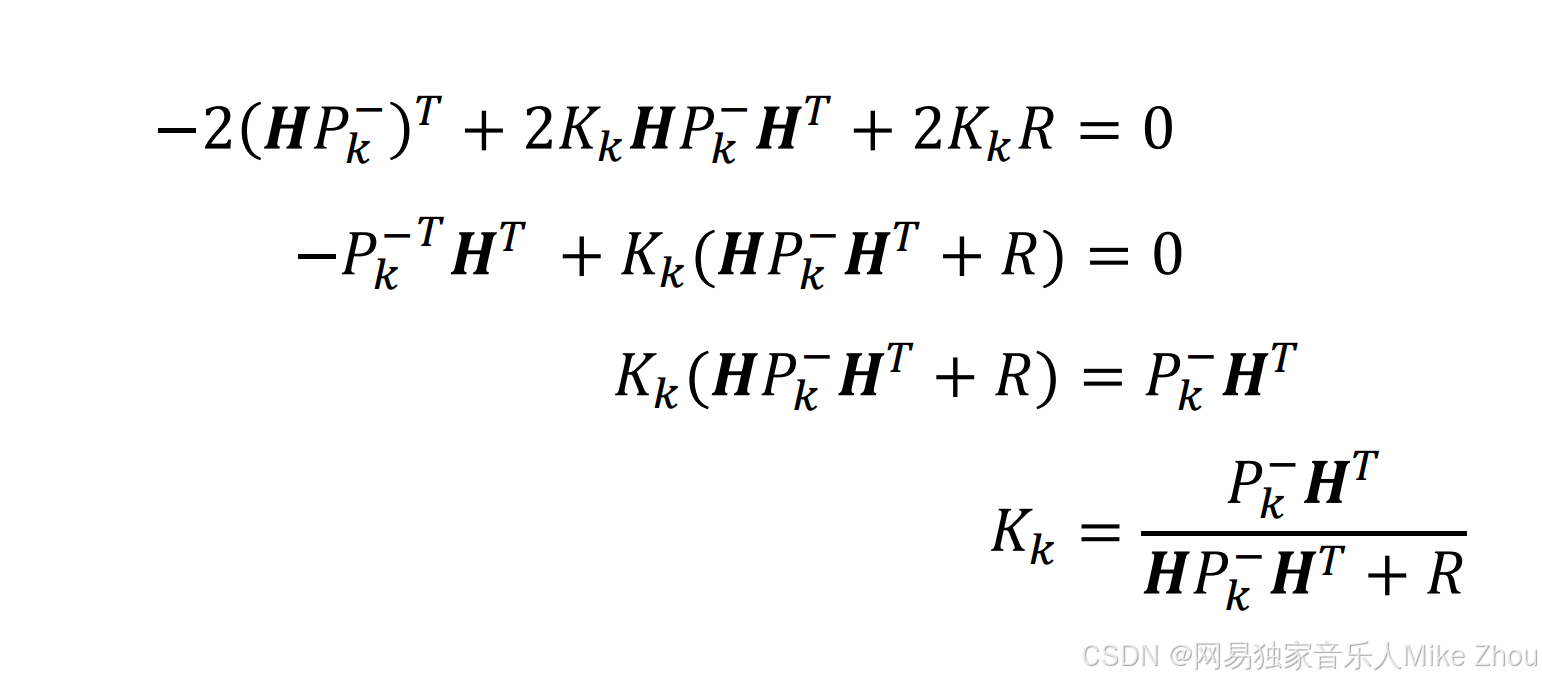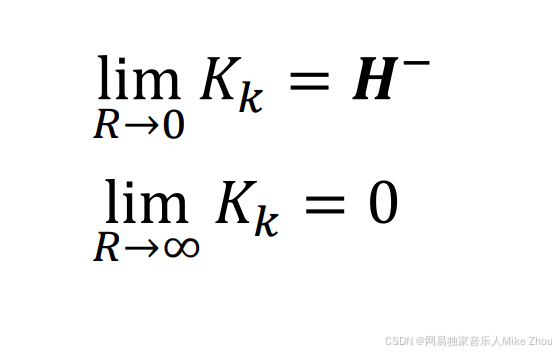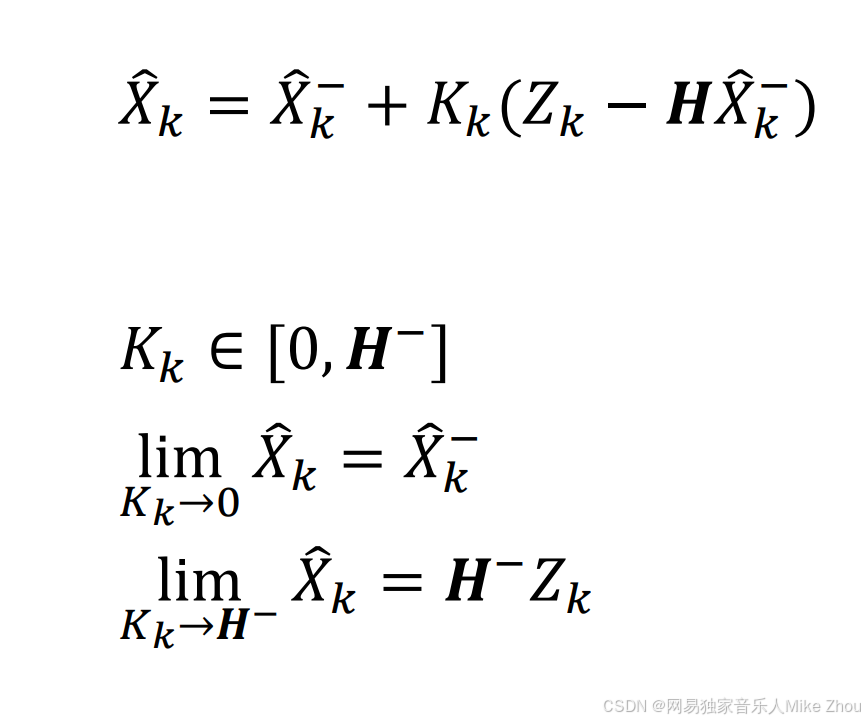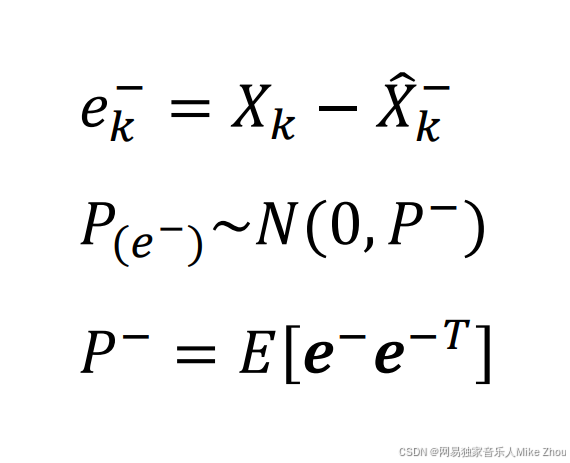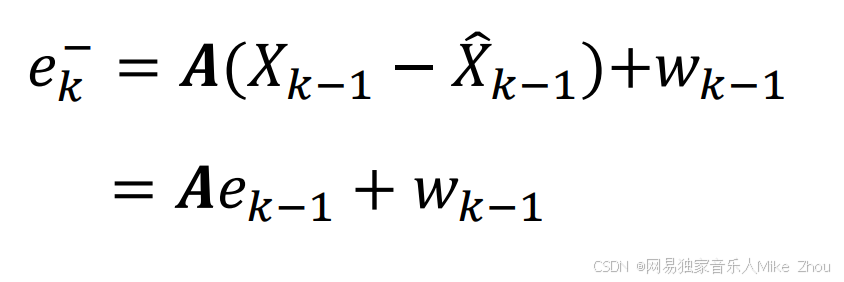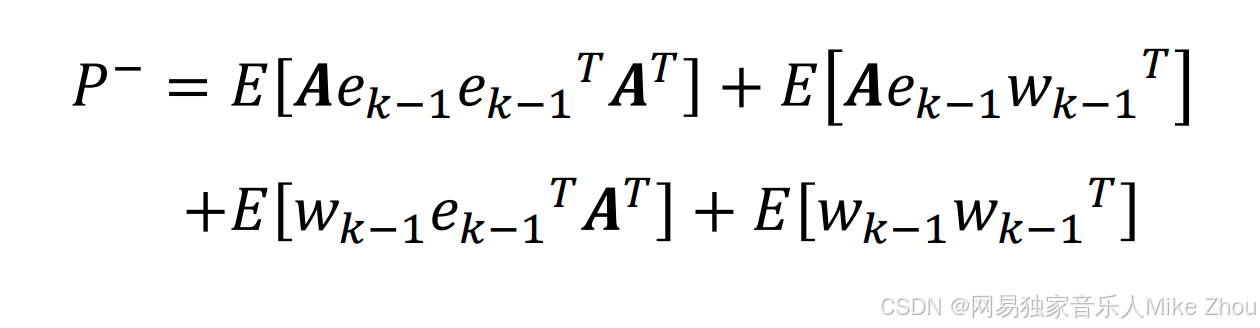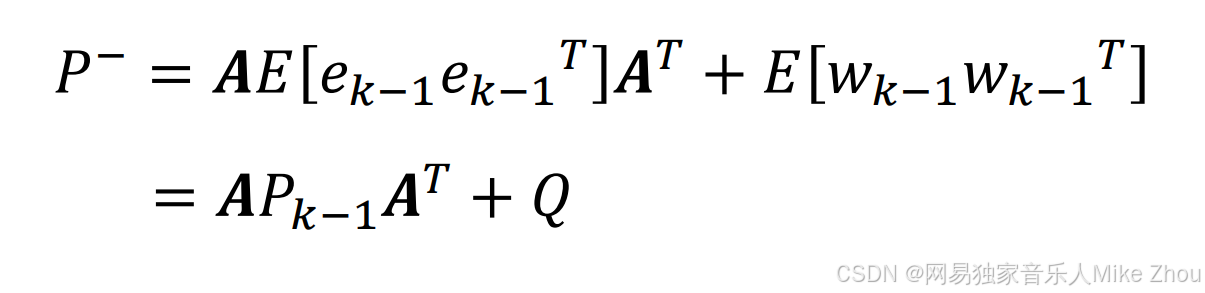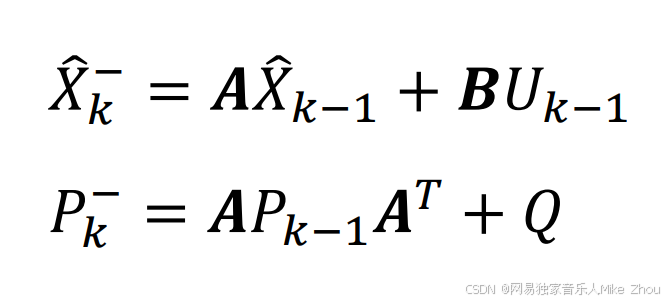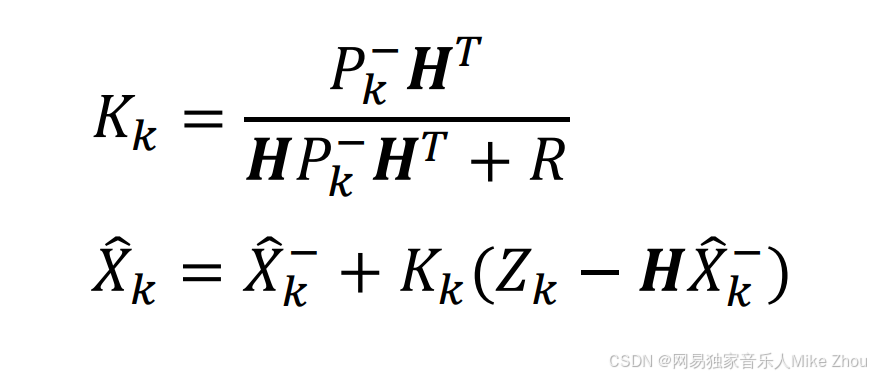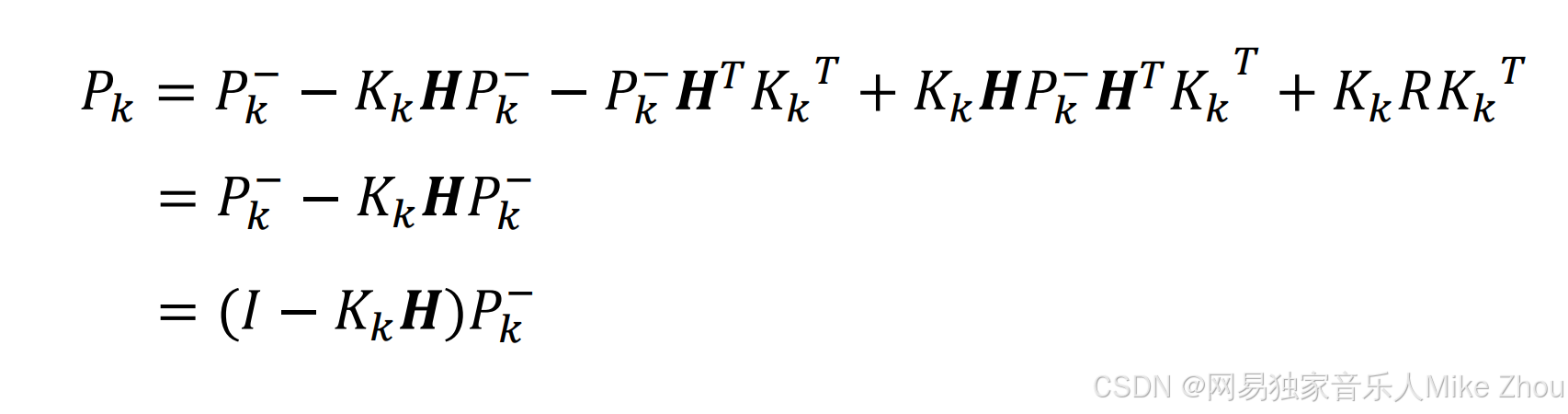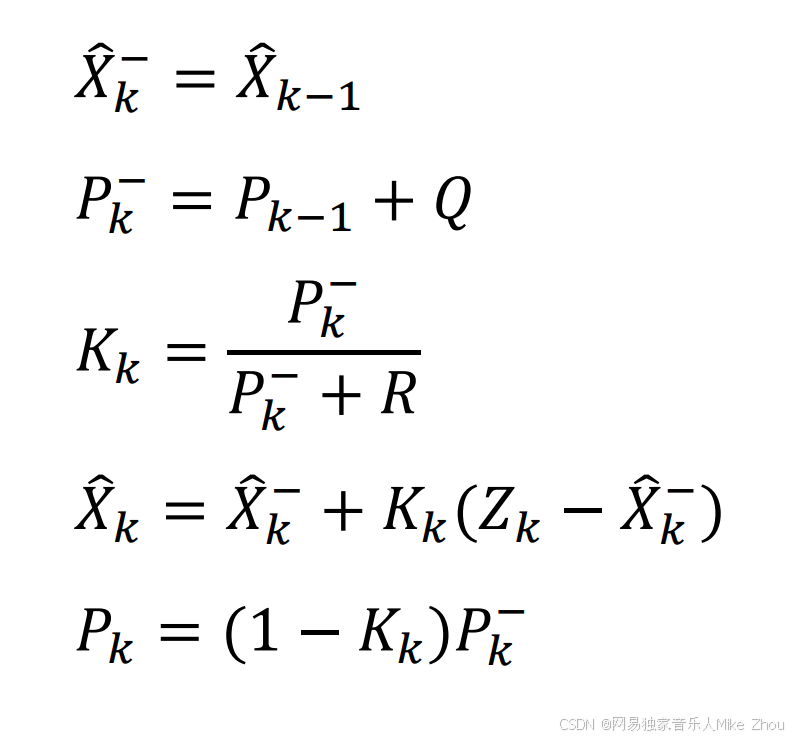【卡尔曼滤波】数据预测Prediction观测器的理论推导及应用 C语言、Python实现（Kalman Filter）

更新以gitee为准：

数据预测概念和适用方式

实际上 数据预测才是卡尔曼滤波器最常见、最普通的功能
通常用在嵌入式领域和现代控制理论中
如传感器数据处理滤波等等
而数据预测在处理数据时 也跟递归一样可以减小方差
但总体而言 数据预测会跟随当前时刻的测量值变化而变化
递归测量到一定次数后则与上一次的估计值相近
这在第一章中我们有探讨
递归的公式中也可以看出来 随着时间增加 K会越来越小

无论是算术平均算法 还是卡尔曼算法 其都会逐渐减小

递归算法 适用条件是在测量静态目标时 由于测量有误差（通常正态分布） 而进行的类似算术平均根的求解
数据预测则适用于线性动态变化的目标

注意是线性 非线性需要用泰勒展开的扩展卡尔曼滤波

数据预测本质上就是将递归算法、数据融合、协方差矩阵等 共同融合起来的一个算法

在数据融合中 我们探讨了估计值与两种不同方式测量值的融合方式
其卡尔曼增益与两种测量方式的方差有关

在协方差矩阵中 两种完全不同的变量 其方差与协方差构成的矩阵可以反应出数据的相关性
协方差越大 数据相关性越强

数据预测则是综合考虑了以上等多方面算法 得出的一个最优解

可以理解成 数据预测就是在变化的数据中 综合考虑了上一次估计值与当前测量值的关系 并将其融合

也就是将一个不太准的计算结果和一个不太准的测量结果进行融合
从而可以用来预测下一时刻的变量变化 （也就是这一时刻到下一时刻的变化）
同时运用在测量方面 也可以有效减小数据的方差（也就是上一时刻到这一时刻的变化）

这就导致了两种情况：

1. 数据变化较大时 譬如从50变化到100 变化量会被拉低 可能最后预测值算出来就是75
2. 数据静态变化时 譬如跟递归算法中的例子相同 数据在一个期望值左右波动 且满足正态分布 预测值会减小方差

线性系统的适用性

另外 在前面两个章节中 都是对静态目标的求解
静态目标肯定是满足线性关系的
但对于非线性系统 普通的卡尔曼滤波算法也就不适用了 必须用扩展卡尔曼滤波

但是在实际应用中 我们可以把每次的数据变化都当作是线性的 因为我们要得到的是稳定后的数据

譬如角度计的值的变化 虽然卡尔曼滤波没法跟踪这种毫无规律的系统
但可以减小整体的方差 并且我们在读值的时候 也是读一个相对静态的值

再比如一个斜率为正值的线性系统 突然斜率为负值了 那么在转折点卡尔曼滤波肯定不适用
但是在斜率为负后 多测几组数据 卡尔曼滤波的误差又会再次收敛

对于完全处于运动状态的系统 普通的卡尔曼滤波就不适用了 这时候本来估计值就是个不准确的值 应选择更加相信测量值而非估计值

数据预测算法和卡尔曼滤波公式推导

一个典型的卡尔曼滤波数据预测例子就是：
一天中 天气的温度变化 满足一定规律 通常是晚上冷 白天热
譬如 20 21 24 28 30 29 26 25 23 22 21
在实际测量中 可能会出现：
20.5 21.3 24.5 28.7 30.1 29.5 26.2 25.4 22.8 22.9 22.1
可以看到 最后一次温度出现了小范围的波动
假如温度计测量误差是0.5 那么这个波动情有可原 这是偶然出现的
这个测量值也并不能说明那个时间点 温度又有了回升
而如果加了卡尔曼滤波 就会将这一部分滤掉 从新变成从低到高 再从高到低的关系
这个是针对线性变化的数据
这个是一维的线性变化
另外 卡尔曼滤波还主要用于数据预测

状态空间方程和观测器

针对某一系统 其随时间变化有一定的规律
根据现代控制理论递归思想 我们可以写成如下形式：

其中 Xk是当前状态变量
X(k-1)是上一时刻的状态变量
A是状态转移矩阵（状态矩阵）
B是控制输入矩阵（控制矩阵）
Uk是当前的控制输入

状态转移矩阵：一个系统的某些因素在转移中，第n次结果只受第n-1的结果影响，即只与当前所处状态有关，而与过去状态无关。
如果是静态系统 那么就是单位矩阵1 但通常写成[1 1 / 0 1]的形式 其模就是1
控制输入矩阵：即改变状态变量的外部输入值
控制输入：外部影响系统变量的输入 如果没有外部扰动 那么通常取0

譬如温度的变化满足一次关系
也就是y=kx+b
那么当前时刻的值 就等于上一时刻的值 加上k*单位时间
譬如y=2k+3

第0时刻为3 第1时刻为5 第2时刻为7…

每一时刻都是上一次时刻的值 加上k*单位时间1 也就是2
那么状态转移矩阵算出来就是2 控制输入矩阵是0

如果 某一时刻 外部输入导致了数据变化 那么控制输入矩阵就不是0了

同时 如果某一时刻对系统进行了加热 那么就有了外部输入 Uk 就需要在数据上再加上一个Uk的值
Uk是一个变化的值 静态时就为0
比如加5度 那么就变成了y=2k+3+5
第0时刻为2 第1时刻为10 第2时刻为12…

同时 如果对该系统进行测量 如果测量准确 则每次测量的结果都是当前的状态变量值
譬如第1时刻温度为5 测量出来也肯定是1*5

可以表达成以下形式：

其中 H是测量矩阵 通常为单位矩阵 写作[1 0 / 0 1]的形式（除非测量结果是成比例不准的 但这几乎不存在 如果存在 人为换算即可）

同时 每次系统的更新都会存在噪声 称为过程噪声或者系统噪声 引入并记为w
譬如就算每小时温度增加1度 但可能某一时刻只增加了0.9度

另外 测量也是有误差的 就像先前数据融合讨论的一样 存在测量噪声 引入并记为v
那么就可以写成如下形式：

次公式就是状态空间方程

过程噪声和测量噪声通常都满足正态分布
且期望值为0
过程噪声的协方差矩阵为Q
测量噪声的协方差矩阵为R

这里的Q、R值可以就直接叫做系统误差和测量误差
同时也是系统噪声和测量噪声的方差

所以本质上卡尔曼滤波 就是用数据融合的思想 融合了系统误差和测量误差 最后得到一个最优的估计值
也就是将一个不太准的计算结果和一个不太准的测量结果进行融合
最后得到的估计值误差要比这两者都要小 所以能有效减小系统数据的方差
同时也能预测下一个时刻的估计值

在预测方面 就是将状态空间方程作为一个观测器使用 已知当前时刻的值 来估计后一时刻的值

先验估计

在状态空间方程中 可以看到状态和误差噪声的关系
如果没有噪声 我们可以直接得到当前的系统变量值：

但噪声是不可避免的
所以我们只能得到估计系统值 记为X_Hat 再加一个上标的-表示算出来的估计值 也就是系统估计值
对于系统估计值X_Hat有以下关系：

也就是上一次的估计值与这一时刻的系统估计值关系

这也就是先验估计

同时 对于测量结果而言 测量估计值与当前测量值的关系为：

也就是测量矩阵的逆矩阵*测量值

这两个算出来的和测出来的X估计值都是不准确的
因为误差没法准确估计

后验估计

得到先验估计以后 我们要引入噪声
那么现在就要用到卡尔曼滤波器 做数据融合 去得到最终的估计值 X_Hat 也就是后验估计

结合卡尔曼滤波的数据融合思想 我们可以定义估计结果为：

其中 G是一个系数
同样 当G为0时 估计值=先验估计值 当G为1时 估计值=测量估计值
也就融合了系统估计值和测量估计值的最终结果
而G的大小决定了是相信根据系统变化规律算出来的结果 还是根据测量算出来的结果

G与卡尔曼增益系数的关系为：

那么方程就写成了：

这里K的取值范围为0到H逆
且：

那么现在就又要找到一个最佳的卡尔曼增益系数 使得估计值最贴近真实值（误差最小）

卡尔曼增益系数计算

不用猜就知道 K的取值与上面提到的系统误差和测量误差有关
引入估计误差ek 则与估计值、真实值的关系为：

e也满足正态分布 且方差为P P也是e矩阵和e矩阵转置的期望

假如有两项e1和e2（也就是两种误差）
则：

那么它的期望就为：

根据概率论公式：

某样本的方差=该样本平方的期望-该样本期望的平方

而对于期望为0的正态分布 该样本期望的平方为0

所以：

其中σ1和σ2就是两种误差的标准差
这就是两种误差的协方差公式

要使误差e的方差P最小 那就是这个协方差矩阵的迹最小
那么就是要找到K 使得以下式子的值最小：

带入估计误差公式得：

其中：

I是单位矩阵

同样 先验也有误差 记为ek上标- 等于实际值与先验估计值的误差

则P就为：

根据公式：

带入得：

对于独立事件A、B有：
E(AB)=E(A)E(B)

所以：

则：

计P上标-为先验误差的方差

则：

同理

所以

即测量误差
代入后得到估计误差的协方差矩阵方程：

它的迹为：

现在要求K 使得迹最小 则就是对dK求导为0：

其中 矩阵相乘的求导公式为：

那么就可以求得卡尔曼增益系数

当R特别大时 Kk趋近于0
当R特别小时 Kk趋近于H的逆矩阵

这就是误差最小时卡尔曼增益的计算公式
再看到先前的公式 满足规律

先验误差协方差矩阵求解

上文提到的先验误差公式：

如果要求Kk则需要先求Pk-
代入先验估计方程：

得到：

还是带入独立事件期望公式
另外 e(k-1)和其转置的期望就是上一次的估计误差协方差矩阵
同时带入系统误差Q
得到当前的先验误差协方差矩阵与上一次的估计误差协方差矩阵的关系：

到此就可以求出卡尔曼滤波的五大公式了 并且可以将其应用出来了

卡尔曼滤波五大公式

进行卡尔曼滤波共有三个部分要做
按步骤顺序分为五个公式

预测

求出先验估计和先验误差协方差矩阵

校正

求出卡尔曼增益和后验估计

更新

代入Kk的值 最后得到Pk
更新估计误差协方差矩阵

公式简化和应用

在嵌入式、现代控制理论中
A矩阵通常为1
B矩阵未知但不受外部输入影响的话 U通常就为0
H矩阵也为1
并且如果是针对静态目标的话 这几项矩阵实际上也就为1

那么就可以简化为以下几个公式
按步骤分别是：

Python实现

上面公式按Python来实现的话就是：

def Prediction(measure,result_last=0,covariance_last=0,Q=0.018,R=0.0542):
    result_priori = result_last
    covariance_priori = covariance_last + Q
    kg = covariance_priori/(covariance_priori + R)
    result_last = result_priori + kg*(measure - result_priori)
    covariance_last = (1-kg)*covariance_priori

    return result_last,covariance_last

运行和调用结果：

v = [10.5,20.6,30.8,40.6,45.3,48.0,47.5,44.5,46.0,43.8,55.5,53.5,56.1,65.2,67.6,68.9,72.2,80.1,81.5,82.6,83.4,84.6,83.5,83.1,85.0,84.5,84.0,83.6,83.9,83.2,84.1,85.6,84.3,84.0,86.5,85.5,85.0,84.8,84.5,84.5,85.1]

a=[]
b=[]
c=[]
d=[]

def Prediction(measure,result_last=0,covariance_last=0,Q=0.018,R=0.0542):
    result_priori = result_last
    covariance_priori = covariance_last + Q
    kg = covariance_priori/(covariance_priori + R)
    result_last = result_priori + kg*(measure - result_priori)
    covariance_last = (1-kg)*covariance_priori

    return result_last,covariance_last

result_last = v[0]
covariance_last = 0

for i in range(len(v)):
    result_last,covariance_last = Prediction(v[i],result_last,covariance_last,5,3)
    a.append(result_last)
    print(result_last)

plt.figure(4)
plt.plot(v,color="g")     
plt.plot(a,color="b")  

10.5
17.531645569620252
26.854454203262236
36.52035749751738
42.694663752563144
46.42567852323806
47.181203021790296
45.29562713905005
45.79098257239374
44.390809326126174
52.20342998159353
53.115252454036465
55.21429828136791
62.23681700454024
66.00851518486351
68.04197330570614
70.96613638757006
77.38959365081972
80.28026737213725
81.91163653085387
82.95833916863266
84.11284931225781
83.68185849247561
83.27266219633323
84.48742530555566
84.49626855259646
84.14726401585693
83.7623965417261
83.85916719333677
83.39560298049119
83.89097540372485
85.09285961415652
84.53527521576893
84.1588389541316
85.80527780658561
85.59058892713347
85.17525288812938
84.9113535140978
84.62206610736457
84.53622221290566
84.93270311901878

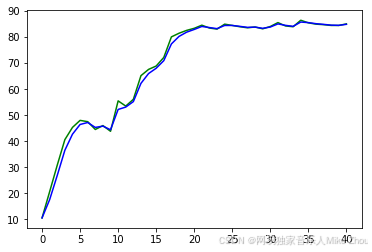
图像：

可以看到蓝线显著在绿线突变时变得平滑

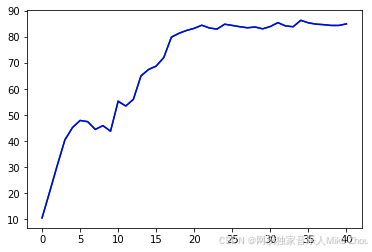
如果减小R 即减小测量误差则会：

表示相信测量结果

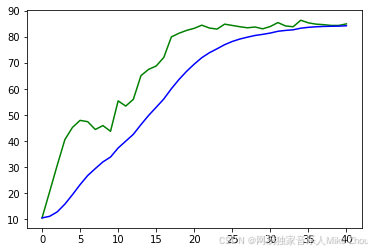
反之减小Q则会：

表示相信先验估计结果

C语言实现

函数：

typedef struct
{
    double Measure_Now;
    double Result_Last;
    double Covariance_Last;
    double Q;
    double R;
}Kalman_Filter_Prediction_Struct;

Kalman_Filter_Prediction_Struct Kalman_Filter_Prediction(Kalman_Filter_Prediction_Struct Stu);

Kalman_Filter_Prediction_Struct Kalman_Filter_Prediction(Kalman_Filter_Prediction_Struct Stu)
{
   double Result_Priori = Stu.Result_Last;
   double Covariance_Priori = Stu.Covariance_Last + Stu.Q;
   double kg = Covariance_Priori/(Covariance_Priori + Stu.R);
   Stu.Result_Last = Result_Priori + kg*(Stu.Measure_Now - Result_Priori);
   Stu.Covariance_Last = (1-kg)*Covariance_Priori;

   return Stu;
}

调用：

void Prediction(void)
{
    double v[41] = {10.5,20.6,30.8,40.6,45.3,48.0,47.5,44.5,46.0,43.8,55.5,53.5,56.1,65.2,67.6,68.9,72.2,80.1,81.5,82.6,83.4,84.6,83.5,83.1,85.0,84.5,84.0,83.6,83.9,83.2,84.1,85.6,84.3,84.0,86.5,85.5,85.0,84.8,84.5,84.5,85.1};

    Kalman_Filter_Prediction_Struct Stu;
    uint8_t i=0;

    Stu.Q=5;
    Stu.R=3;    
    Stu.Covariance_Last=0.0f;
    Stu.Result_Last=v[0];

    for(i=0;i<41;i++)
    {
        Stu.Measure_Now=v[i];
        Stu = Kalman_Filter_Prediction(Stu);
        printf("%f \n",Stu.Result_Last);
    }
}

调用结果：

10.500000 
17.531646 
26.854454 
36.520357 
42.694664 
46.425679 
47.181203 
45.295627 
45.790983 
44.390809 
52.203430 
53.115252 
55.214298 
62.236817 
66.008515 
68.041973 
70.966136 
77.389594 
80.280267 
81.911637 
82.958339 
84.112849 
83.681858 
83.272662 
84.487425 
84.496269 
84.147264 
83.762397 
83.859167 
83.395603 
83.890975 
85.092860 
84.535275 
84.158839 
85.805278 
85.590589 
85.175253 
84.911354 
84.622066 
84.536222 
84.932703

与Python保持一致

附录：压缩字符串、大小端格式转换

压缩字符串

首先HART数据格式如下：


重点就是浮点数和字符串类型
Latin-1就不说了 基本用不到

浮点数

浮点数里面 如 0x40 80 00 00表示4.0f

在HART协议里面 浮点数是按大端格式发送的 就是高位先发送 低位后发送

发送出来的数组为：40,80,00,00

但在C语言对浮点数的存储中 是按小端格式来存储的 也就是40在高位 00在低位
浮点数：4.0f
地址0x1000对应00
地址0x1001对应00
地址0x1002对应80
地址0x1003对应40

若直接使用memcpy函数 则需要进行大小端转换 否则会存储为：
地址0x1000对应40
地址0x1001对应80
地址0x1002对应00
地址0x1003对应00

大小端转换：

void swap32(void * p)
{
   uint32_t *ptr=p;
   uint32_t x = *ptr;
   x = (x << 16) | (x >> 16);
   x = ((x & 0x00FF00FF) << 8) | ((x >> 8) & 0x00FF00FF);

   *ptr=x;
}

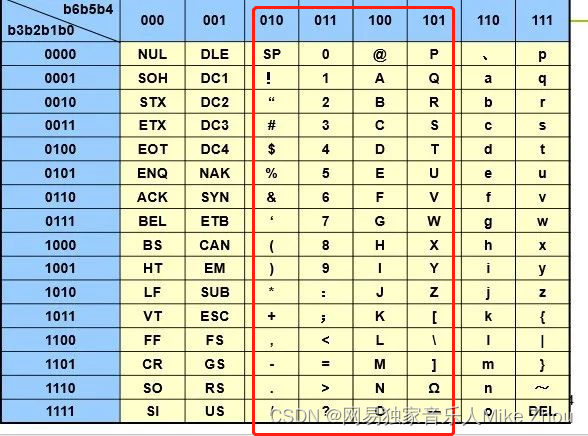
压缩Packed-ASCII字符串

本质上是将原本的ASCII的最高2位去掉 然后拼接起来 比如空格(0x20)
四个空格拼接后就成了
1000 0010 0000 1000 0010 0000
十六进制：82 08 20
对了一下表 0x20之前的识别不了
也就是只能识别0x20-0x5F的ASCII表

压缩/解压函数后面再写：

//传入的字符串和数字必须提前声明 且字符串大小至少为str_len 数组大小至少为str_len%4*3 str_len必须为4的倍数
uint8_t Trans_ASCII_to_Pack(uint8_t * str,uint8_t * buf,const uint8_t str_len)
{
   if(str_len%4)
   {
      return 0;
   }
	 
   uint8_t i=0;
   memset(buf,0,str_len/4*3);	  
   for(i=0;i<str_len;i++)
   {
      if(str[i]==0x00)
      {
         str[i]=0x20;
      }
   }

   for(i=0;i<str_len/4;i++)
   {
      buf[3*i]=(str[4*i]<<2)|((str[4*i+1]>>4)&0x03);
      buf[3*i+1]=(str[4*i+1]<<4)|((str[4*i+2]>>2)&0x0F);
      buf[3*i+2]=(str[4*i+2]<<6)|(str[4*i+3]&0x3F);
   }

   return 1;
}

//传入的字符串和数字必须提前声明 且字符串大小至少为str_len 数组大小至少为str_len%4*3 str_len必须为4的倍数
uint8_t Trans_Pack_to_ASCII(uint8_t * str,uint8_t * buf,const uint8_t str_len)
{
   if(str_len%4)
   {
      return 0;
   }

   uint8_t i=0;

   memset(str,0,str_len);

   for(i=0;i<str_len/4;i++)
   {
      str[4*i]=(buf[3*i]>>2)&0x3F;
      str[4*i+1]=((buf[3*i]<<4)&0x30)|(buf[3*i+1]>>4);
      str[4*i+2]=((buf[3*i+1]<<2)&0x3C)|(buf[3*i+2]>>6);
      str[4*i+3]=buf[3*i+2]&0x3F;
   }

   return 1;
}