Day12

第一题

蓝桥杯算法提高

打水问题

贪心

要想让等待时间最短，就要尽可能的使打水时间少的先分配到水龙头，所以我们可以把时间排序，按照下标依次分配水龙头。

前m个人已经占用了m个水龙头，那么第m + 1个人应该该排在第1个水龙头，第m + 2个人应该该排在第2个水龙头，第m + k个人应该该排在第k个水龙头，这样就可以使时间最短。

import java.util.Scanner;
import java.util.Arrays;

public class Main {

    static final int N = 1010;
    static int[] t = new int[N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), m = sc.nextInt();
        for (int i = 0; i < n; i++) t[i] = sc.nextInt();
        Arrays.sort(t, 0, n);

        int sum = 0;
        for (int i = m; i < n; i++) { // i从m开始枚举 小于n 分配水龙头
            int j = i;
            while (j - m >= 0) {
                sum += t[j - m];
                j -= m;
            }
        }
        System.out.println(sum);
    }
}

第二题

蓝桥杯算法提高

夺宝奇兵

递推

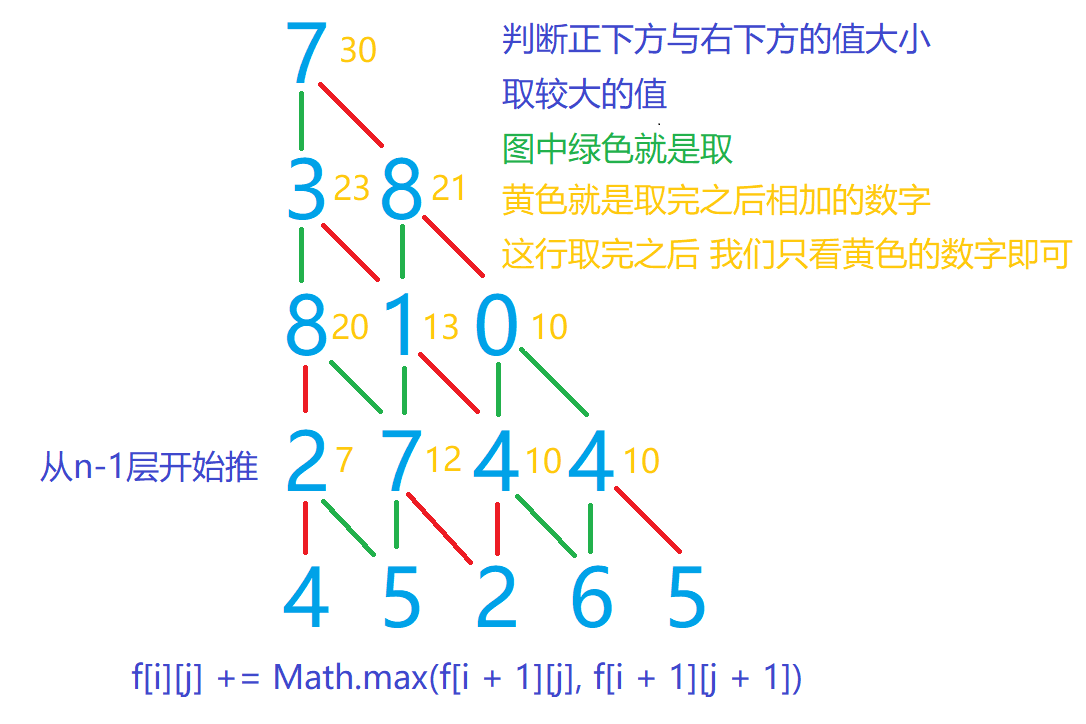
这道题就是数字三角形。

解决这道问题的方法有很多，动态规划，枚举，但是我们最简单的方式就是用递推式求解。

import java.util.Scanner;

public class Main {

    static final int N = 110;
    static int[][] f = new int[N][N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= i; j++)
                f[i][j] = sc.nextInt();

        for (int i = n - 1; i >= 1; i--) {
            for (int j = 1; j <= n; j++) {
                f[i][j] += Math.max(f[i + 1][j], f[i + 1][j + 1]); // 是它正下方的值大还是右下方的值大
            }
        }

        System.out.println(f[1][1]); // 最后爬到顶端就是我们的最大值
    }
}

第三题

第九届2018年蓝桥杯国赛

调手表

C++B组第4题

bfs

广搜出来的每一个时间点的步数都是最小步数，最后遍历一遍答案即可。

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {

    static final int N = 100010;
    static int[] a = new int[N];
    static int n, k;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        k = sc.nextInt();

        bfs();

        int ans = 0;
        for (int i = 1; i < n; i++) ans = Math.max(ans, a[i]);

        System.out.println(ans);
    }

    private static void bfs() {
        Queue<PII> q = new LinkedList<>();
        q.offer(new PII(0, 0));

        while (!q.isEmpty()) {
            PII t = q.poll();
            int x = t.x, y = t.y; // x是时间 y是步数
            if (x + 1 < n && a[x + 1] == 0) {
                a[x + 1] = y + 1;
                q.offer(new PII(x + 1, y + 1));
            }
            if (a[(x + k) % n] == 0) {
                a[(x + k) % n] = y + 1;
                q.offer(new PII((x + k) % n, y + 1));
            }
        }
    }

    static class PII {
        int x;
        int y;

        public PII(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }
}