算法
算法定义
- 是对特定问题求解步骤的一种描述,是指令的有限序列。
- 算法五大特征
- 输入:有0个或多个输入;
- 输出:有1个或多个输出;
- 有限性:算法有限步结束,指令有限时间完成;
- 确定性:每条指令有确切含义;
- 可行性:每个运算可由计算机有限条指令完成。
算法举例(递归)
定义
- 所谓递归,从字面意思可以看出有两个过程:“递去”和“归来”,即在“递去”过程中满足某个条件后进行“归来”。
- 绝大数编程语言支持函数的自调用,在这些函数可以通过调用自身来进行递归。
举例
- 整数n的阶乘(n!)
- 代码如下
long long recursion1(int n) //long long 类型防止结果溢出
{
if (n == 1 || n==0)
{
return 1;
}
return n * recursion1(n - 1);
}
// n=6---->返回720```
- 过程分析
| 函数 | 递去 ⇓ \Downarrow ⇓ | 是否满足if? | 归来 ⇑ \Uparrow ⇑ |
|---|---|---|---|
| recursion1(6) | 6 × r e c u r s i o n 1 ( 5 ) 6\times recursion1(5) 6×recursion1(5) | 否 | 6 × 5 × 4 × 3 × 2 × 1 6\times5\times4\times3\times2\times1 6×5×4×3×2×1 |
| 6 × r e c u r s i o n 1 ( 5 ) 6\times recursion1(5) 6×recursion1(5) | 6 × 5 × r e c u r s i o n 1 ( 4 ) 6\times5\times recursion1(4) 6×5×recursion1(4) | 否 | 5 × 4 × 3 × 2 × 1 5\times4\times3\times2\times1 5×4×3×2×1 |
| 6 × 5 × r e c u r s i o n 1 ( 4 ) 6\times5\times recursion1(4) 6×5×recursion1(4) | 6 × 5 × 4 × r e c u r s i o n 1 ( 3 ) 6\times5\times4\times recursion1(3) 6×5×4×recursion1(3) | 否 | 4 × 3 × 2 × 1 4\times3\times2\times1 4×3×2×1 |
| 6 × 5 × 4 × r e c u r s i o n 1 ( 3 ) 6\times5\times4\times recursion1(3) 6×5×4×recursion1(3) | 6 × 5 × 4 × 3 × r e c u r s i o n 1 ( 2 ) 6\times5\times4\times3\times recursion1(2) 6×5×4×3×recursion1(2) | 否 | 3 × 2 × 1 3\times2\times1 3×2×1 |
| 6 × 5 × 4 × 3 × r e c u r s i o n 1 ( 2 ) 6\times5\times4\times3\times recursion1(2) 6×5×4×3×recursion1(2) | 6 × 5 × 4 × 3 × 2 × r e c u r s i o n 1 ( 1 ) 6\times5\times4\times3\times2\times recursion1(1) 6×5×4×3×2×recursion1(1) | 否 | 2 × 1 2\times1 2×1 |
| 6 × 5 × 4 × 3 × 2 × r e c u r s i o n 1 ( 1 ) 6\times5\times4\times3\times2\times recursion1(1) 6×5×4×3×2×recursion1(1) | 6 × 5 × 4 × 3 × 2 × 1 6\times5\times4\times3\times2\times1 6×5×4×3×2×1 | 是,开始归来 ⇑ \Uparrow ⇑ | 1 |
结果为720
递归与循环
- 我们首先引用知乎用户李继刚link对递归和循环的生动解释:
- 递归:你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,你继续打开它。若干次之后,你打开面前的门后,发现只有一间屋子,没有门了。然后,你开始原路返回,每走回一间屋子,你数一次,走到入口的时候,你可以回答出你到底用这你把钥匙打开了几扇门。
- 循环:你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,若前面两扇门都一样,那么这扇门和前两扇门也一样;如果第二扇门比第一扇门小,那么这扇门也比第二扇门小,你继续打开这扇门,一直这样继续下去直到打开所有的门。但是,入口处的人始终等不到你回去告诉他答案。
- 对于一些简单的算法,与循环相比,我们可以直观的看出递归算法的朴素与简洁;
- 从算法本身出发,递归与循环并无优劣之分;但循环并不需要对函数进行重复调用,效率往往比递归效率高。
算法性能分析与度量
算法效率的评价方法
- 事后统计
- 将算法实现,统计其时间和空间开销;
- 事前分析
- 对算法所消耗时间和空间资源的一种估计方法。
算法效率分析——时间复杂度
算法的运行时间
⇒
每
条
语
句
执
行
次
数
之
和
⇒
基
本
语
句
执
行
次
数
\Rightarrow每条语句执行次数之和\Rightarrow基本语句执行次数
⇒每条语句执行次数之和⇒基本语句执行次数
=
每
条
语
句
执
行
时
间
之
和
=每条语句执行时间之和
=每条语句执行时间之和
=
执
行
次
数
×
=执行次数\times
=执行次数× 执行一次的时间
⇒
\Rightarrow
⇒指令系统、代码质量有关
定义
- 算法的运行时间可表示为基本语句执行次数,它是问题规模的函数;
- 称这个函数的渐进阶为算法的时间复杂度。
程序步
- 不严格的定义:
- 一个程序步是一个在语法上或语义有意义的程序片段,且该程序片段的执行时间不依赖实力特性。
各种语句的程序步数
- 注释语句:非执行语句,程序步数为0;
- 声明语句:程序步数为0;
- 定义变量和常量的语句(int、long、double等)
- 允许用户自定义数据类型(class、struct等)
- 判断访问权限的语句(private、public等)
- 描述函数特性的语句(void、virtual)
- 表达式和赋值语句:大部分程序步数为1,例外是表达式中包含函数调用;
- 循环语句:仅考虑语句中 控制部分 的程序步数;
for(<初始化语句>;<表达式1>;<表达式 2>)
while<表达式>do
do...while<表达式>
- whille和do语句控制部分每次执行的程序步数等于<表达式>的程序步数;
- for语句的 控制部分 每次执行步数都等于1,除非<初始化语句>、<表达式1>或<表达式 2>为实例性函数。
- 注:循环语句的程序步数为控制部分执行次数,而非循环执行次数,所以对于for(<初始化语句>;<表达式1>;<表达式 2>)和while<表达式>do语句来说,
循
环
语
句
程
序
步
数
=
循
环
执
行
次
数
+
1
循环语句程序步数=循环执行次数+1
循环语句程序步数=循环执行次数+1;
而对于do…while<表达式>语句来说,因为是先执行后控制判断,所以 循 环 语 句 程 序 步 数 = 循 环 执 行 次 数 循环语句程序步数=循环执行次数 循环语句程序步数=循环执行次数。
- switch语句:由一个首部加上一个或多个条件语句组成。
switch(<表达式>)
{
case cond1:<语句1>
case cond2:<语句2>
...
default:<语句>
}
- 其中,首部 switch(<表达式>)的时间开销等于<表达式>的时间开销;每个条件语句的时间开销等于该条件语句自身加上其前面条件语句的时间开销。
- if-else语句:由3部分构。
if(<表达式>)<语句1>; else<语句2>;每个部分程序步数分别根据<表达式>、<语句1>或<语句2>的程序步数来确定。
- 函数调用:所有函数调用的程序步数都为1,除非函数调用涉及与实例特性有关的按值参数传递。
- 内存管理语句:new、delete和sizeof,程序步数为1。
- 转移语句:包括continue,break,goto,return和return<表达式>,程序步数为1。除非<表达式>为 实例性函数。
计算程序步数的两种方法
实例如下,计算程序的程序步数:
float Sum(float * data, const int num)
{
float s = 0 ;
for(int i=0; i<num; i++){
s += a[i] ;
}
return s ;
}
- 全局count法:定义一个全局变量count初始为0,插入到程序中:
float Sum(float * data, const int num)
{
float s = 0 ;
count++ ;//变量s赋值
for(int i=0; i<num; i++){
count++ ;//for语句
s += a[i] ;
count++ ;//表达式
}
count++ ;//for语句最后一次控制判断
count++ ;//转移语句 return
return s ;
}
//进一步化简
float Sum(float * data, const int num)
{
for(int i=0; i<num; i++){
count +=2 ;
}
count +=3 ;
}
可见程序步数为 2 n u m + 3 2num+3 2num+3。
- 列表法: 程 序 步 数 = 每 条 语 句 执 行 一 次 的 程 序 步 数 × 执 行 次 数 程序步数=每条语句执行一次的程序步数\times执行次数 程序步数=每条语句执行一次的程序步数×执行次数
| 行 | s/e | 语句频率 | 程序步数 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 2 | 1 | 1 | 1 |
| 3 | 1 | n u m + 1 num+1 num+1 | n u m + 1 num+1 num+1 |
| 4 | 1 | n | n |
| 5 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 |
| 总的程序步数 | 2 n u m + 3 2num+3 2num+3 |
表示方法
-
T ( n ) = O ( f ( n ) ) T(n)=O(f(n)) T(n)=O(f(n))
- 若 存 在 两 个 正 常 数 c 和 n 0 , 对 任 意 n ≥ n 0 , 都 有 T ( n ) ≤ c × f ( n ) , 则 称 T ( n ) = O ( f ( n ) ) 若存在两个正常数c和n_0,对任意n\ge n_0,都有T(n)\le c \times f(n),则称T(n)=O(f(n)) 若存在两个正常数c和n0,对任意n≥n0,都有T(n)≤c×f(n),则称T(n)=O(f(n));
- 给出算法复杂度上界,不可能比 c × f ( n ) c\times f(n) c×f(n)更大。
- 例:
T
(
n
)
=
6
×
2
n
+
n
2
T(n)=6\times 2^n+n^2
T(n)=6×2n+n2
- 当 n ≥ 4 时 , 6 × 2 n + n 2 ≤ 6 × 2 n + 2 n = 7 × 2 n , 因 此 T ( n ) = O ( 2 n ) 当n\ge4时,6\times 2^n+n^2\le6\times 2^n+2^n=7\times2^n,因此T(n)=O(2^n) 当n≥4时,6×2n+n2≤6×2n+2n=7×2n,因此T(n)=O(2n).
-
T ( n ) = Ω ( f ( n ) ) T(n)=\Omega(f(n)) T(n)=Ω(f(n))
- 若 存 在 两 个 正 常 数 c > 0 和 n 0 ≥ 1 , 使 当 n ≥ n 0 , 都 有 T ( n ) ≥ c × f ( n ) , 则 称 T ( n ) = O ( f ( n ) ) 若存在两个正常数c>0和n_0\ge1,使当n\ge n_0,都有T(n)\ge c \times f(n),则称T(n)=O(f(n)) 若存在两个正常数c>0和n0≥1,使当n≥n0,都有T(n)≥c×f(n),则称T(n)=O(f(n));
- 给出算法复杂度下界,不可能比 c × f ( n ) c\times f(n) c×f(n)更小。
- 例:
T
(
n
)
=
3
n
3
+
2
n
2
T(n)=3n^3+2n^2
T(n)=3n3+2n2
- 取 c = 3 , n 0 = 1 , f ( n ) = n 3 , 则 当 n ≥ n 0 时 , 有 3 n 3 + 2 n 2 ≥ 3 n 3 , 因 此 T ( n ) = Ω ( n 3 ) 取c=3,n_0=1,f(n)=n^3,则当n\ge n_0时,有3n^3+2n^2\ge 3n^3,因此T(n)=\Omega(n^3) 取c=3,n0=1,f(n)=n3,则当n≥n0时,有3n3+2n2≥3n3,因此T(n)=Ω(n3).
-
T ( n ) = Θ ( f ( n ) ) T(n)=\Theta(f(n)) T(n)=Θ(f(n))
- 若 存 在 c 1 , c 2 > 0 和 n 0 ≥ 1 , 使 当 n ≥ n 0 , 都 有 T ( n ) ≤ c 1 × f ( n ) 和 T ( n ) ≥ c 2 × f ( n ) , 则 称 T ( n ) = Θ ( f ( n ) ) 若存在c_1,c_2>0和n_0\ge1,使当n\ge n_0,都有T(n)\le c_1 \times f(n)和T(n)\ge c_2 \times f(n),则称T(n)=\Theta(f(n)) 若存在c1,c2>0和n0≥1,使当n≥n0,都有T(n)≤c1×f(n)和T(n)≥c2×f(n),则称T(n)=Θ(f(n));
- 给出算法复杂度下界和下界
- 例:
T
(
n
)
=
3
n
3
+
2
n
2
T(n)=3n^3+2n^2
T(n)=3n3+2n2
- 取 c 1 = 5 , c 2 = 3 , n 0 = 1 , f ( n ) = n 3 , 则 当 n ≥ n 0 时 , 有 3 n 3 + 2 n 2 ≤ 5 n 3 和 3 n 3 + 2 n 2 ≥ 3 n 3 , 因 此 T ( n ) = Θ ( n 3 ) 取c_1=5,c_2=3,n_0=1,f(n)=n^3,则当n\ge n_0时,有3n^3+2n^2\le 5n^3和3n^3+2n^2\ge 3n^3,因此T(n)=\Theta(n^3) 取c1=5,c2=3,n0=1,f(n)=n3,则当n≥n0时,有3n3+2n2≤5n3和3n3+2n2≥3n3,因此T(n)=Θ(n3).
常用的时间复杂度
- O ( 1 ) : 常 量 阶 O(1):常量阶 O(1):常量阶
- O ( n ) : 线 性 阶 O(n):线性阶 O(n):线性阶
- O ( log k n ) : 对 数 阶 O(\log_k n):对数阶 O(logkn):对数阶
- O ( n log k n ) : 线 性 对 数 阶 O(n\log_k n):线性对数阶 O(nlogkn):线性对数阶
- O ( n k ) : k ≥ 2 , k 次 方 阶 O(n^k):k\ge 2,k次方阶 O(nk):k≥2,k次方阶
- 大小比较:
- O ( 1 ) ≤ O ( log k n ) ≤ O ( n ) ≤ O ( n log k n ) ≤ O ( n k ( k ≥ 2 ) ) ≤ O ( 2 n ) ≤ O ( n ! ) O(1)\le O(\log_k n)\le O(n)\le O(n\log_k n)\le O(n^k(k\ge2))\le O(2^n)\le O(n!) O(1)≤O(logkn)≤O(n)≤O(nlogkn)≤O(nk(k≥2))≤O(2n)≤O(n!)
- 指数时间的关系大小:
- O ( 2 n ) < O ( n ! ) < O ( n n ) O(2^n)<O(n!)<O(n^n) O(2n)<O(n!)<O(nn)
- 一般的,常用 最深层循环内 的语句中的原操作的执行频度(重复次数)来表示。
- 当 n n n取的很大时,指数时间算法和多项式时间算法在所需时间上非常悬殊。
算法效率分析——空间复杂度
- 指算法在执行过程中所需最大存储空间;
- 空间复杂性的渐进分析: S ( n ) = O ( f ( n ) ) S(n)=O(f(n)) S(n)=O(f(n)).
- 例:
- 一 维 数 组 a [ n ] : S ( n ) = O ( n ) 一维数组a[n]:S(n)=O(n) 一维数组a[n]:S(n)=O(n);
- 二 维 数 组 a [ n ] [ m ] : S ( n ) = O ( n × m ) 二维数组a[n][m]:S(n)=O(n\times m) 二维数组a[n][m]:S(n)=O(n×m)
总结—基本概念
上一篇:数据结构-基本概念–数据
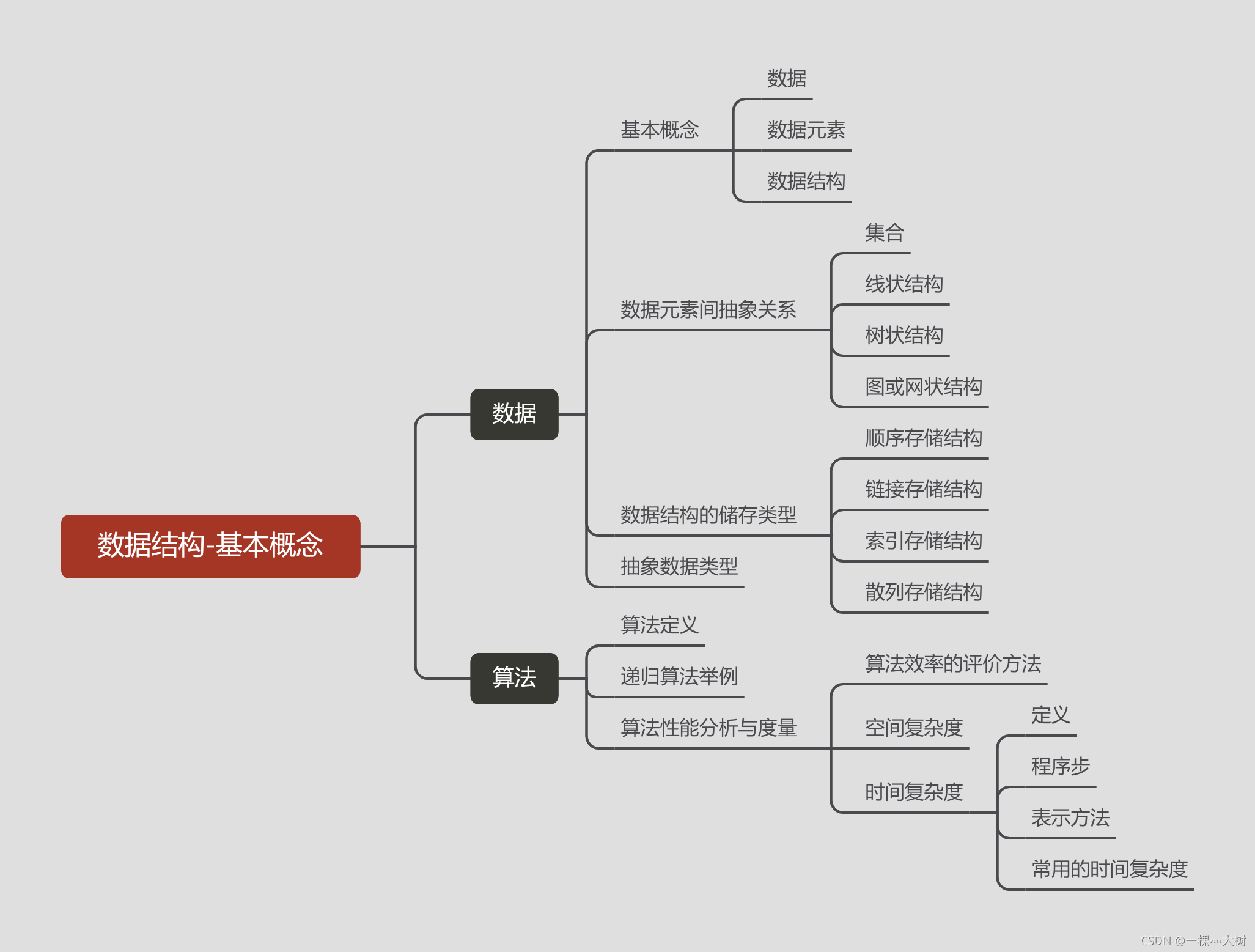
思维导图