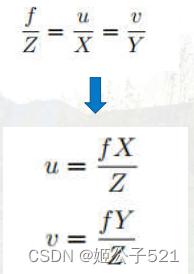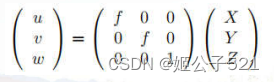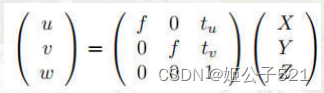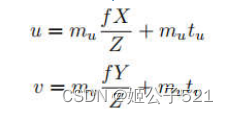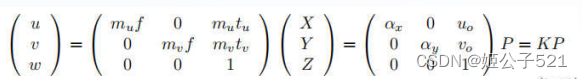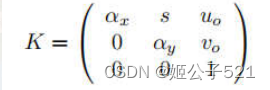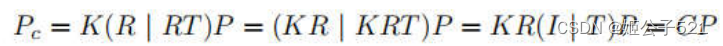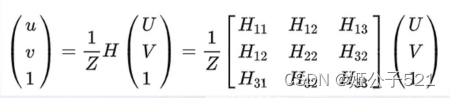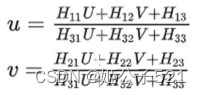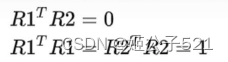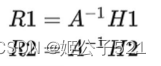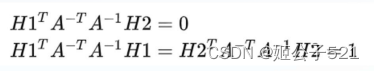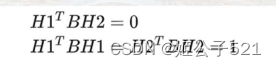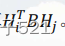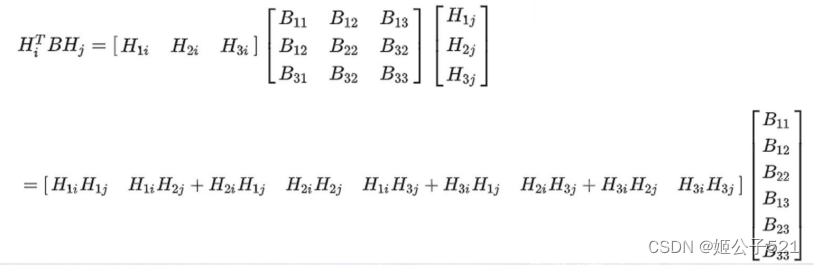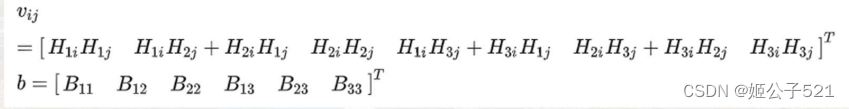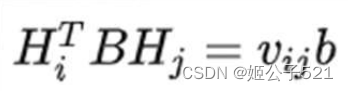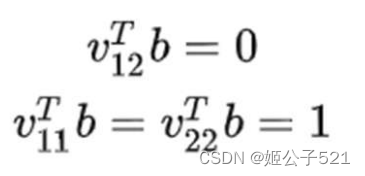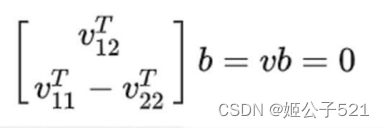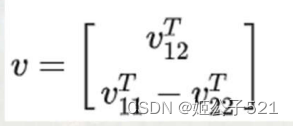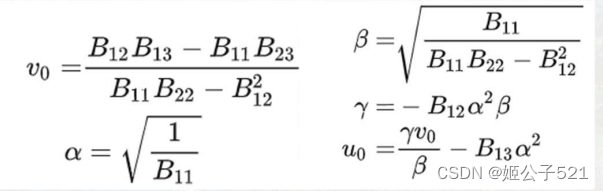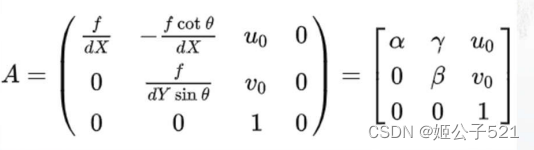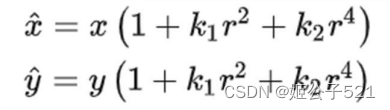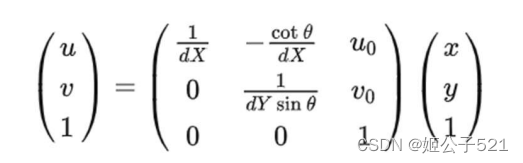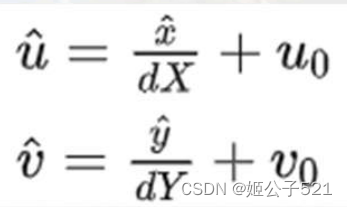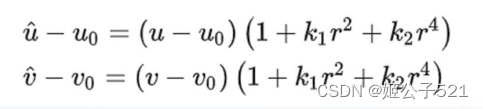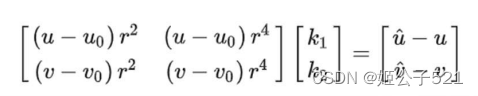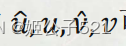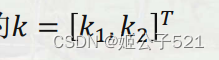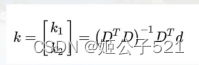本文参考王坤峰老师《计算机视觉》的课上PPT,如有错误,欢迎指正!
一、内参矩阵
针孔摄像机示意图如下:
由相似三角形(标黄色)可得:
使用齐次坐标:(可理解为上式的u,v等式最后一行还有个1=1,然后三个式子左右均乘上一个Z,那么1=1就变成了Z=Z,用w代替左边的Z,即为下式中的w=Z)
不过这是一个理想的情况,即相机图像平面平行于XY平面,其原点在主轴与像平面的交点。
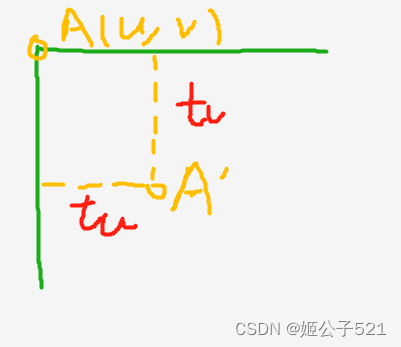
假设图像平面的原点与Z轴与图像平面相交的点不重合。在这种情况下,我们需要将Pc平移到期望的原点。(向模型中添加新的参数)
如上图,A点为理想情况,A’为现在要考虑的偏移情况。偏移的x轴的分量为tu,y轴的分量为tv,那么此时u=f * X / Z + tu,v=f * Y /Z + tv。使用齐次坐标可得:
在上式中,单位为英寸。而在相机图像中,我们需要用像素为单位。
为此,我们需要知道相机中的分辨率或像素密度。
如果像素是正方形的,u和v两个方向上
有相同分辨率。
然而,对于更一般的模型,我们假设在u和v方向上分辨率分别为mu和mv。因此,为了以像素为单位来测量,它的u和v坐标应该分别乘以mu和mv。
即为:
进一步转换:
上式中的K仅取决于相机内部参数,如焦距、主轴、像素大小和分辨率。这些参数被称为摄像机的内参。
如果图像平面不是一个标准矩形,即像平面轴彼此不正交(剪切变换),则K还包括一个扭曲参数s作为
二、外参矩阵
现在,考虑这样一种情况:相机的投影中心不在(0,0,0),主轴不在Z轴上,图像平面虽然仍然与主轴正交,但也不平行于XY平面。在这种情况下,我们必须首先使用一个变换矩阵,使得相机的投影中心与(0,0,0)重合,主轴与Z轴重合,像平面的u轴与X轴对齐(或像平面的v轴与Y轴对齐),即像平面平行于XY平面。
这个转换首先是通过一个平移变换将投影的中心移动到原点,然后通过一个旋转变换来对齐主轴和Z轴。
设这个平移矩阵为T(Tx, Ty, Tz)。让主轴与Z轴重合的旋转
矩阵由3×3旋转矩阵R给出,子矩阵相乘得到3×4变换矩阵
E被称为外参矩阵。注意,由于现在使用了平移,我们也必须使用齐次坐标表示
P。所以,P到Pc的完整变换矩阵为:
其中,3×4矩阵C通常被称为相机标定矩阵。这里,P用四维齐次坐标(X, Y, Z, 1)表示,由CP导出的Pc使用三维齐次坐标(u, v, w)。
因此,通过对三维齐次坐标进行归一化,即(u/w, v/w, 1),可以得到相机像平面上投影的精确二维位置。
内参矩阵自由度为5(2个为投影中心的位置,2个为像素在两个方向上的大小,1个扭曲因子)。
而外参矩阵有6个自由度(平移和旋转各3个)。
因此,C有11个自由度。这可以表明,C的右下角元素将永远是1。
三、张正友标定法
张正友标定法标定相机的内外参数的思路如下:
1)求解内参矩阵与外参矩阵的积
2)求解内参矩阵
3)求解外参矩阵
1、求解内参矩阵与外参矩阵的积
将世界坐标系固定于棋盘格上,则棋盘格上任一点的物理坐标W=0,因此,原单点无畸变的成像模型可以化为下式。其中,R1,R2为旋转矩阵R的前两列。为了简便,将内参矩阵记为 A。
对于不同的图片,内参矩阵A为定值;对于同一张图片,内参矩阵A,外参矩阵(R1,R2,T)为定值;对于同一张图片上的单点,内参矩阵A,外参矩阵(R1,R2,T),尺度因子 Z 为定值。
将A(R1,R2,T)记为矩阵H,H即为内参矩阵和外参矩阵的积,记矩阵H的三列为(H1,H2,H3),则有:
利用上式,消去尺度因子Z:
此时,尺度因子 Z已经被消去,因此上式对于同一张图片上所有的角点均成立。
(u,v)是像素坐标系下的标定板角点的坐标, (U,V)是世界坐标系下的标定板角点的坐标。
通过图像识别算法,我们可以得到标定板角点的像素坐标(u,v),又由于标定板的世界坐标系是人为定义好的,标定板上每一个格子的大小是已知的,我们可以计算得到世界坐标系下的(U,V)。
由这里的 H 是齐次矩阵,有8个独立未知元素。每一个标定板角点可以提供两个约束方程(u,U,V的对应关系、v,U,V的对应关系提供了两个约束方程),因此,当一张图片上的标定板角点数量等于4时,即可求得该图片对应的矩阵H。
当一张图片上的标定板角点数量大于4时,利用最小二乘法回归最佳的矩阵H。
2、求解内参矩阵
已知了矩阵H=A(R1 R2 T),接下来需要求解相机的内参矩阵A。
利用R1,R2作为旋转矩阵 R的两列,存在单位正交的关系,即:
则由 H和R1,R2的关系,可知:
代入:
另外,上述两个约束方程中均存在矩阵A的转置乘矩阵A的逆,将它记为B,则B为对称矩阵。
先试图求解出矩阵B, 通过矩阵B再求解相机的内参矩阵A。
同时,为了简便,记相机内参矩阵A:
可得B:
注意:由于B为对称阵,上式出现了两次B12, B13, B23。
再次转化:
因此,为了求解矩阵B,必须计算
这里i可以为1,2;j可以为1,2
简记为:
则:
此时,通过R1,R2单位正交得到的约束方程可化为:
转化:
由于矩阵 H已知,矩阵v又全部由矩阵 H 的元素构成,因此矩阵v已知。
此时,只要求解出向量 b,即可得到矩阵B。
每张标定板图片可以提供一个 v * b =0 的约束关系,该约束关系含有两个约束方程。
但是,向量b有6个未知元素。因此,单张图片提供的两个约束方程是不足以解出来向量b的。
因此,只要取3张标定板照片,得到3个 v * b =0 的约束关系,即6个方程,即可求解向量b。
当标定板图片的个数大于3时(事实上一般需要15到20张标定板图片),可采用最小二
乘拟合最佳的向量 b,并得到矩阵B。
根据矩阵B的元素和相机内参的对应关系(如上式),可得到:
求得内参矩阵:
3、求解外参矩阵
外参矩阵反映的是标定板和相机的位置关系。对于不同的图片,标定板和相机的位置关系已经改变,此时每一张图片对应的外参矩阵都是不同的。
在关系:A (R1 R2 T)= H中,已经求解得到了矩阵H(对于同一张图片相同,对于不同的图片不同)、矩阵A(对于不同的图片都相同)。
通过公式: (R1 R2 T)= A^(-1) H. ,即可求得每一张图片对应的外参矩阵 (R1 R2 T)
由于张正友标定板将世界坐标系的原点选取在棋盘格上,则棋盘格上任一点的物理坐标W=0,将旋转矩阵的R的第三列R3消掉,因此R3在坐标转化中并没有作用。但是 R3要使得R满足
旋转矩阵的性质,即列与列之间单位正交,因此可以通过向量 R1,R2的的叉乘,即R3=R2 x R1,计算得到R3.
此时,相机的内参矩阵和外参矩阵均已得到。
4、标定相机的畸变参数
张正友标定法仅仅考虑了畸变模型中影响较大的径向畸变。
径向畸变公式(2阶)如下:
(r^2 = x^2 +y^2)
像素坐标和图像坐标的转化关系为:
其中, (u,v)为理想的无畸变的像素坐标。由于角度接近于90°,则上式近似为:
可得畸变后的像素坐标:
代入径向畸变公式(2阶)则有:
即为:
上式中的
可以通过识别标定板的角点获得,每一个角点可以构造两个上述等式。有m幅图像,每幅图像上有n个标定板角点,则将得到的所有等式组合起来,可以得到个mn未知数为的
约束方程,将约束方程系数矩阵记为 D ,等式右端非齐次项记为 d ,可将其记着矩阵形式: Dk=d
则使用最小二乘法可求得:
此时,相机的畸变矫正参数已经标定好。
上述公式推导的时候以2阶径向畸变为例,但实际上更高阶的径向畸变同理,只是需要的约束方程个数更多而已。