写在前面的注意点：

• scanf函数是有返回值的，返回被输入函数成功赋值的变量个数。
  如：scanf ("%d",&n) != EOF 常在while()中使用
  如果输入已经到达结尾（输入文件到达末尾或在命令台输入中输入Ctrl+z），scanf函数无法再为变量n赋值，于是scanf函数返回EOF（end of file）
• 开数组要开在main函数外面，另外数组不能开得过大，比如1000010000的二维数组绝对内存超限了，10001000左右的没问题
• 奇偶是%2 二分类，013是%3 三分类，…依此类推
• 读文件输入测试用例：#include<cstdio> //需要引入的库, freopen("input.txt","r",stdin); //提交时把这行注释掉就行
• int<10的9次方，long long小于10的18次方
• 有一些题目需要先输入一个整数，然后输入多行字符串，这时候如果用gets、getline之类用来输入字符串的函数，都会把换行给接收到，导致输入的结果有问题。这时候可以考虑用getchar来接收整数后的换行，使后续的整行字符串能顺利读入。
• memset函数在string.h或cstring头文件下，可以将数组中每个元素以字节为单位赋值,最常见的就是赋值0或者-1。memset(a,0,sizeof(a))
• - 单点测试：如PAT，1个case输入；1个输出结果。
  - 多点测试：如大多数OJ

（1）while-EOF型：多个case输入，至文件结束，while(scanf(xxx)!=EOF 或 cin>>xxx ){ 执行程序操作 }；一行一个结果输出。 在while循环中，cin只有在遇到文件结束符(end-of-file)，或遇到一个无效输入时（例如输入的值不是一个整数），cin>>xxx返回cin，cin的状态会变为无效false退出循环。从键盘输入文件结束符(end-of-file): 在Windows系统中，输入文件结束符的方法是按Ctrl+Z，然后按Enter或Return键。

（2）while(n–)型：先输入case个数n，再输入多个case，int n;scanf("%d",&n);while(n--){执行程序操作}；一行一个结果输出。
- 输出格式：
（1）空格单行输出：printf("%d ",a);
（2）连续多行输出：printf("%d\n",a);
（3）连续空行输出：printf("%d\n\n",a);
（4）连续多行输出，但最后一组数据后无空行：这种一般是在while(n–)类型中，只需判断n是否已经减小到0，即while(n--){ printf("%d",a); if(n>0)printf("\n"); } 空格单行，最后无空格同理

• 背模板。其实PAT考来考去也就那么几种类型的题，常用的算法和语法模板背一下，最重要的包括：

自定义 STL中的sort规则，知道如何给结构体数组排序
vector, stack, queue, map等STL库的常规用法
并查集及路径压缩
Dijkstra最短路径算法（常规版+DFS版）
Hash表的查找模拟及hash冲突解决模拟
DFS，BFS
二叉树的遍历（前中后序+层序）
二叉树的重建（如根据前序+中序）
AVL树的判断（树的构造能写更好，不过感觉略难，考的几率不大）
数学类（素数判断、最大公约数、质因子分解等）

第一题（20分）常考数学类、逻辑类题目。如涉及到素数、最大公约数，或者自己定义一个规则，让你求或者判断这种特定的数，编程难度低（会写for循环就能做），需要认真读懂题目。建议过样例用时不超过25分钟。
第二题（25分）常考简单数据结构及应用。如栈、链表、哈希、结构体等，常见的是排序题，给出一堆数据，按要求排序（链表题本质也是结构体的排序题）。建议过样例用时不超过30分钟。
第三题（25分）常考树或图。如二叉树的重建、并查集等套路题的变形，或者是给出一些经典树、图，让你判断（红黑树、拓扑排序、欧拉图等），其实比较简单，别被吓到，根据定义来就行。建议过样例用时不超过30分钟。
第四题（30分）常考树或图。如最短路径、最近公共祖先、堆的判断等。这类题目往往也不难，但一般代码量较大，很可能需要DFS及剪枝。建议过样例用时不超过1小时。

1. 排序

$$一个sort走天下$$

快速排序 ：$O(n\ast logn)$

C++已经为我们编写了快速排序库函数sort和qsort，实际解题过程中，我们只需调用该函数，便能轻易的完成快速排序。

qsort是C的函数，在“stdlib.h”头文件中；
sort是C++的函数，在"algorithm"头文件中，最大对30w的数据排序。

qsort和sort用法上最大的不同在于比较函数上，qsort的比较函数必须是int (*fcmp)(const void *,const void *)（留意其形参的类型），返回正/0/负，而sort的比较函数则没有这样的要求，返回true/false。

//（待排序数组首地址/迭代器,待排序数组尾地址/迭代器，[比较函数]）
void sort(first, first+n, bool cmp);

忘记cmp函数的升序降序时，只需现场用int型测试一下即可!!!!! 不用死记硬背
cmp返回的bool指L是否小于R！！！

// 从小到大排(int型)
bool cmp (int L,int R) { //定义排序规则：相邻元素
	return L<R;
}
// 从大到小排(int型)
bool cmp (int L,int R) { //定义排序规则：相邻元素
	return L>R;
}

常考的是：自定义函数的多级排序(结构体排序)

• sort是不稳定的排序，若需要先进入的等值元素排在前面，则需要稳定排序stable_sort函数，用法和sort一样。

• sort：(推荐！)

#include<algorithm>
//（待排序数组首地址,待排序数组尾地址，[比较函数]）
//不写比较函数，默认升序，仅适用于int/double/char等基本类型
void sort(first, first+n, bool cmp);

// 比较函数：返回true/false,升序(L>R return flase)
// int型降序排序
bool cmp (int L,int R) { //定义排序规则
	return L > R;
}

// char型降序排序
bool cmp (char L,char R) { //定义排序规则
	return L > R;
}

// 字符串升序 (二维字符数组，每行为一个英文单词)
int cmp( char *s1, char *s2){
	int flag= strcmp(s1, s2)
	if(flag<0) return true;
	else return false;
}

// 字符串降序 (二维字符数组，每行 为一个英文单词)
int cmp( char *s1, char *s2){
	int flag= strcmp(s1, s2)
	if(flag>0) return true;
	else return false;
}

// 结构体MyStruct数组,优先对x升序，当x相等时，对y降序，排序
struct MyStruct{
	int x,y;
};
int cmp( MyStruct& L, MyStruct& R){//&引用避免复制开销
	if(L.x>R.x) return false;
	else if(L.x<R.x) return true; 
	else if(L.x==R.x){
		if(L.y<R.y) return true;
		else return false;
	}
}

例题：有 N 个学生的数据，将学生数据按成绩高低排序，如果成绩相同则按姓名字符的字母序排序，如果姓名的字母序也相同则按照学生的年龄排序，并输出> N个学生排序后的信息。

测试数据有多组，每组输入第一行有一个整数 N（N<=1000），接下来的 N行包括 N 个学生的数据。每个学生的数据包括姓名（长度不超过 100 的字符串）、年龄（整形数）、成绩（小于等于 100 的正数）。

样例输入：
3
abc 20 99
bcd 19 97
bed 20 97

样例输出：
bcd 19 97
bed 20 97
abc 20 99

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std; 
struct E { 
char name[101]; 
int age; 
int score; 
}buf[1000]; 
bool cmp(E a,E b) { //实现比较规则
if (a.score != b.score) return a.score < b.score; //若分数不相同则分数低者在前
int tmp = strcmp(a.name,b.name); 
if (tmp != 0) return tmp < 0; //若分数相同则名字字典序小者在前
else return a.age < b.age; //若名字也相同则年龄小者在前
} 
int main () { 
int n; 
while (scanf ("%d",&n) != EOF) { 
 for (int i = 0;i < n;i ++) { 
 scanf ("%s%d%d",buf[i].name,&buf[i].age,&buf[i].score); 
 } // 输入
 sort(buf,buf + n,cmp); //利用自己定义的规则对数组进行排序
 for (int i = 0;i < n;i ++) { 
 printf ("%s %d %d\n",buf[i].name,buf[i].age,buf[i].score); 
 } //输出排序后结果
} 
return 0; 
} 

建立了 cmp 函数，该函数是重点，便可作为计算机对其进行排序的依据，也可以直接定义该结构体的小于运算符。

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std; 
struct E { 
char name[101]; 
int age; 
int score; 
bool operator < (const E &b) const { //利用C++算符重载直接定义小于运算符
 if (score != b.score) return score < b.score; 
 int tmp = strcmp(name,b.name); 
 if (tmp != 0) return tmp < 0; 
 else return age < b.age; 
} 
}buf[1000]; 
int main () { 
int n; 
while (scanf ("%d",&n) != EOF) { 
 for (int i = 0;i < n;i ++) { 
 scanf ("%s%d%d",buf[i].name,&buf[i].age,&buf[i].score); 
 } 
 sort(buf,buf + n); 
 for (int i = 0;i < n;i ++) { 
 printf ("%s %d %d\n",buf[i].name,buf[i].age,buf[i].score); 
 } 
} 
return 0; 
}

建议使用第二种方法（重载运算符）。这样，首先可以对重载算符的写法有一定的了解；其次，在今后使用标准模板库时，该写法也有一定的用处。
有了 sort函数，你所需要做的只是按照题面要求为其定义不同的排序规则即可，不会再对排序问题感到恐惧。

海量排序：机试很少考较难。
以下都是一些数据很特殊且数据量非常大的情况下的解决方案。

1.如果题目给的数据量很大，上百万的数据要排序，但是值的区间范围很小，比如值最大只有10万，或者值的范围在1000W到1010W之间，对于这种情况，我们可以采用空间换时间的计数排序(开一个计数数组，每出现一次计数+1)。

2、字符串的字典序排序是一个常见的问题，需要掌握，也是用sort，结合string对象的compare函数实现。

3、如果题目给你一个数的序列，要你求逆序数对(a[i]>a[i+1])有多少，这是一个经典的问题，解法是在归并排序合并是进行统计，复杂度可以达到nlogn。如果数据量小，直接冒泡排序即可。

4、如果题目让你求top10，即最大或最小的10个数，如果数据量很大，建议使用选择排序，也就是一个一个找，这样复杂度比全部元素排序要低。

5、如果题目给的数据量有几百万，让你从中找第K大的元素，这时候sort是会超时的。解法是利用快速排序的划分的性质，进入到其中一个分支继续寻找。

针对上述数据量较大的排序，可以使用partial_sort()排序函数：（位于 <algorithm> 头文件中）

//按照默认的升序排序规则，对 [first, last) 范围的数据进行筛选并排序
void partial_sort (RandomAccessIterator first,
                   RandomAccessIterator middle,
                   RandomAccessIterator last);
//按照 comp 排序规则，对 [first, last) 范围的数据进行筛选并排序
void partial_sort (RandomAccessIterator first,
                   RandomAccessIterator middle,
                   RandomAccessIterator last,
                   Compare comp);

其中，first、middle 和 last 都是随机访问迭代器，comp 参数用于自定义排序规则。
partial_sort() 函数会以交换元素存储位置的方式实现部分排序的。具体来说，partial_sort() 会将 [first, last) 范围内最小（或最大）的 middle-first 个元素移动到 [first, middle) 区域中，并对这部分元素做升序（或降序）排序。

需要注意的是，partial_sort() 函数受到底层实现方式的限制，它仅适用于普通数组和部分类型的容器：

• 容器支持的迭代器类型必须为随机访问迭代器。这意味着，partial_sort() 函数只适用于 array、vector、deque 这 3 个容器。
• 当选用默认的升序排序规则时，容器中存储的元素类型必须支持 <小于运算符；同样，如果选用标准库提供的其它排序规则，元素类型也必须支持该规则底层实现所用的比较运算符；
• partial_sort() 函数在实现过程中，需要交换某些元素的存储位置。因此，如果容器中存储的是自定义的类对象，则该类的内部必须提供移动构造函数和移动赋值运算符。

2. Hash散列

这里的 Hash映射表 旨在讲述其在机试试题解答中的作用，而不像《数据结构》教科书上，对各种 Hash 方法、冲突处理做过多的阐述。

当我们已知输入的范围和具体的个数时，可以利用与数组下标对应的方法，分别统计各数出现的次数。

int Hash[101] = {0};//初始时，我们将数组初始化为 0，代表着每一个分数出现的次数都是 0

利用读入的数直接作为数组下标来访问该元素，因此这个过程十分快捷，进行Hash[x]++。当输入完成后，Hash 数组中就已经保存了每一个数出现的次数。当我需要查询 数 x 出现的次数时，只需访问统计其出现次数的数组元素 Hash[x],便能得知答案。

//假如输入范围是1-100的整数，统计输入n个数的次数
int n,x,a[101],find;
    cin>>n;
    for (int i = 1; i < 101; i++) a[i]=0;
    for (int i = 0; i < n; i++){
        cin>>x;
        a[x]++;
    }
    //查看find的在n个输入中的个数
    cin>>find;
    cout<<a[find]<<endl;

若输入数据中出现了负数，于是我们不能直接把输入数据当做数组下标来访问数组元素，而是将每一个输入的数据都加上一个固定的偏移值。

如果输入范围非常大，哈希属于空间换时间的操作，需要注意定义的哈希数组的长度是否过大，如a[SIZE];：
①分配在静态空间，在栈上（局部变量）或全局静态区（全局变量）上分配的，一般栈的内存是1M到2M，所以静态分配的空间不能太大，比如如果定义a[1024*1024];运行时就会报”段错误“，遇到要申请大的空间时，就需要动态申请。
②函数内申请的变量，数组，是在栈（stack）中申请的一段连续的空间。栈的默认大小为2M或1M，开的比较小；
③全局变量，全局数组，静态数组（static）则是开在全局区（静态区）（static）。大小为2G，所以能够开的很大；
④而malloc、new出的空间，则是开在堆（heap）的一段不连续的空间。理论上则是硬盘大小。
综上，将哈希数值定义为全局数值较为常见。

例.“臭味相投”——这是我们描述朋友时喜欢用的词汇。两个人是朋友通常意味着他们存在着许多共同的兴趣。然而作为一个宅男，你发现自己与他人相互了解的机会并不太多。幸运的是，你意外得到了一份北大图书馆的图书借阅记录，于是你挑灯熬夜地编程，想从中发现潜在的朋友。
首先你对借阅记录进行了一番整理，把N个读者依次编号为1,2,…,N，把M本书依次编号为1,2,…,M。同时，按照“臭味相投”的原则，和你喜欢读同一本书的人，就是你的潜在朋友。你现在的任务是从这份借阅记录中计算出每个人有几个潜在朋友。

输入描述:
每个案例第一行两个整数N,M，2 <= N ，M<= 200。接下来有N行，第i(i = 1,2,…,N)行每一行有一个数，表示读者i-1最喜欢的图书的编号P(1<=P<=M)

输出描述:
每个案例包括N行，每行一个数，第i行的数表示读者i有几个潜在朋友。如果i和任何人都没有共同喜欢的书，则输出“BeiJu”（即悲剧，^ ^）

示例1 输入
4 5
2
3
2
1

输出
1
BeiJu
1
BeiJu

#include<iostream>
using namespace std;

int main(){
    int n,m,a[201]={0},hash[201]={0};
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>a[i]; //a[i]表示第i个读者喜欢的书号
        hash[a[i]]++; //书号喜欢的人数++
    }
    for(int i=0;i<n;i++){
        if(hash[a[i]]==1) cout<<"BeiJu"<<endl;
        else cout<<hash[a[i]]-1<<endl;
    }
    return 0;
}

3.模拟

3.1 简单模拟

简单模拟不涉及太多算法，题目怎么说，你就怎么做。考察基本代码能力。
题目都很基础，自己去PTA上刷几道就知道了。
比如什么水仙花数之类的…

下面列举一道，在我刷本章题的过程中，遇到的一个比较有意思的问题，它源自"三位数"，但把原来的3位整数改为了任意位整数。

eg.给定一个三位数，输出它的百位、十位、个位。
在一行中先后输出的百位、十位、个位，中间用空格隔开，行末不允许有多余空格。
输入 823
输出 8 2 3

如果是三位数，我们只需暴力求解三位数的各个位即可

#include <cstdio>

int main() {
    int n;
    scanf("%d", &n);
    printf("%d %d %d", n / 100, n % 100 / 10, n % 10);
    return 0;
}

但如果扩展到了任意位，位数不固定，就无法暴力求解。

eg，要求输出 任意长度整数 的 各个位，输出行末无多余空格。
样例.
输入 8231834
输出 8 2 3 1 8 3 4

思想：取位只能通过%10获得最后一位，先进后出(递推/栈)，即可顺序获得所有位。
代码1(递推)：

#include<iostream>
using namespace std;

void cout_wei(int num,int verify){
    if(num/10==0){
        cout<<num<<" "; 
        return;
    }
    cout_wei(num/10,-1);
    
    if(num==verify) 
        cout<<num%10;
    else 
        cout<<num%10<<" ";
}

int main(){
    int num;
    cin>>num;
    cout_wei(num,num);
    return 0;
}

代码2(栈)：

#include <iostream>
#include <stack>
using namespace std;

int main() {
    int x;
    cin >> x;
    stack<int> s;
    while (x) s.push(x % 10), x /= 10;
    while (!s.empty()) cout << s.top() << ' ', s.pop();
    //(注意 这里我懒得写最后判断多余的空格了)
    return 0;
}

3.2 提示信息

同时要注意题目给的提示条件，一定会派上用场，否则不就白给了嘛。

如果测试样例非常大，比如2的98314次方，那么pow函数就会输出负数，这里提示就很有用了，可以自己实现2的n次方，在*2的过程中每次都可以%1007，使得x永远不大于1007。

#include<iostream>
using namespace std;


int main(){
    int x=1,n;
    cin>>n;
    for (int i = 0; i < n; i++) {
        x = (x * 2) % 1007; //每次都可以%1007，使得x永远不大于1007
    }
    cout<<x%1007;
    return 0;
}

3.3 查找

查找不仅会在题目中直接单独考察(本小节所讲)，同时也可能是其他算法中的重要组成部分(STL的find函数)。

• 顺序查找：如果需要在一个比较小范围的数据集里进行查找，那么直接遍历每一个数据即可;O(n)
• 二分/红黑树查找：如果需要查找的范围比较大，那么可以用map / sort+二分查找等算法来进行更快速的查找。O(logn)

查找题型：
1、数字查找：给你一堆数字，让你在其中查找x是否存在。 题目变形：如果x存在，请输出有几个。
2、字符串查找：给你很多个字符串，让你在其中查找字符串s是否存在。

不能用顺序查找：
1、数据量特别大的时候，比如有10W个元素。
2、查询次数很多的时候，比如要查询10W次。

解决办法：map容器！！！（底层是红黑树实现的，也就意味着它的插入和查找操作都是logn级别的，复杂度和二分查找是一个量级的，且更加简便，可以通过99.9%的静态/动态查找题目）
map.find(key)!=map.end()就是查到了
map[key]返回对应值

动态查找：数的集合在不断的改变。如果我们用先排序再二分的方法就会遇到困难，因为加入新的数的时候我们需要去移动多次数组，才能将数插入进去，最坏情况每次插入都是O(n)的复杂度，这是无法接受的。但用map来解决这个问题就很简单：

if(map.find(key)!=map.end()) return map[key];//查到就返回
else map[key]=val;//没查到就向map中添加

二分查找：当然不是说二分查找就没用了，我们也需要了解二分查找的原理(左右取中间)，只不过。二分的前提是单调性，只要满足单调性就可以二分，不论是单个元素还是连续区间。$$map=sort排序+二分查找$$

STL内置find()复杂度：
algorithm的find 复杂度是O(n)，对vector，string等 顺序查询。
map::find 和 set::find 复杂度是O(logn)，因为map和set底层都是红黑树。

3.4 图形

两种输出图像的方法：

• 通过数学规律，直接进行输出。
• 定义一个二维字符数组，通过规律填充之，然后输出整个二维数组。

3.5 日期

日期问题中处理平年/闰年 和 大月/小月问题，比较繁琐，需要耐心处理即可。
日期格式限制：

// 输出日期 2019-01-01
int year,month,day;
scanf("%d-%d-%d",&year,&month,&day);
printf("%d-%02d-%02d\n",year,month,day); //0填充，2位宽

// 输入时间 12:12:12
int hour,minute,second;
scanf("%d:%d:%d",&hour,&minute,&second);
printf("%02d:%02d:%02d\n",hour,minute,second);

经典例题：
求两个YYYYMMDD日期之间的天数(包括这两天)。

解题思路：

• 建平润年表：months[13][2],j=平年0，闰年1
• 判断闰年：被4且不被100整除 或 被400整除
• 取y m d：用%和/运算
• 累加day(核心思想：d每+1进行一次判断，是否m要+1，是否y要+1)，d=每月最大天数+1时，m++；m=13时，y++。

#include <cstring>
#include <iostream>
using namespace std;

//建平年/闰年数组，j=平年0，闰年1
int months[13][2]={
  {0,0}, //空出第0行，只看1-13行，共12个月
  {31,31},//1月
  {28,29},
  {31,31},
  {30,30},
  {31,31},
  {30,30},
  {31,31},
  {31,31},
  {30,30},
  {31,31},
  {30,30},
  {31,31},
};

//判断闰年(被4且不被100整除 或 被400整除)
int isLeep(int year){
  //平年0，闰年1
  if((year%4==0 && year%100!=0)||(year%400==0))
    return 1;
  else
    return 0;
}

int main( ){ 
  int temp1,temp2,y1,y2,m1,m2,d1,d2;
  while(cin>>temp1>>temp2)//若输入成功进入while
  {
    if (temp1>temp2){//temp1小于temp2
      int temp=temp1;
      temp1=temp2;
      temp2=temp;
    }
    //从YYYYMMDD中提取YYYY,MM,DD
    y1=temp1/10000;
    m1=temp1%10000/100;
    d1=temp1%100;

    y2=temp2/10000;
    m2=temp2%10000/100;
    d2=temp2%100;
    
    int days=1;//初始天数差=1
    while (y1<y2||m1<m2||d1<d2){
      //day不断从temp1增加到temp2
      d1++;
      if(d1==months[m1][isLeep(y1)]+1){
        ++m1;
        d1=1;
      }
      if(m1==13){
        ++y1;
        m1=1;
      }
      ++days;            
    }
    cout<<days<<endl;   
  }    
  return 0;
}

3.6 进制转换

本质是数位拆解问题

P进制 转换为 Q进制：

Step1：P进制数x -> 10进制数y:末位累加法

• x=a1a2a3a4…an
• y=a1* P(n-1次方) + a2* P(n-2次方) + … + an-1* P(1次方)+an

适用于2和8和16进制(可能有ABCDE！！！)：
k进制数 radixK(字符串) -> 10进制数 radix10

#include <cstdio>
#include <cstring>

const int MAXN = 8;
char radixK[MAXN];

int main() {
    int k;
    scanf("%s %d", radixK, &k);
    int radix10 = 0, base = 1, lenRadixK = strlen(radixK);
    for (int i = lenRadixK - 1; i >= 0; i--) {
        int thisPosition = (radixK[i] >= '0' && radixK[i] <= '9') ? (radixK[i] - '0') : (radixK[i] - 'A' + 10);
        radix10 += thisPosition * base;
        base *= k;
    }
    printf("%d", radix10);
    return 0;
}

Step2：10进制数y -> Q进制数:除基取余法
如10进制数11->2进制数，不断除基Q，余数数组z倒过来(从z[num-1]到z[0])，逐位输出，即为结果。

适用于2和8和16进制(可能有ABCDE！！！)：
10进制数 radix10 -> k进制数/字符串 radixK

#include <cstdio>

const int MAXN = 11;
int radixK[MAXN], len = 0;

int main() {
    int radix10, k;
    scanf("%d%d", &radix10, &k);
    do {
        radixK[len++] = radix10 % k;
        radix10 /= k;
    } while (radix10 > 0);
    for (int i = len - 1; i >= 0; i--) {
        if (radixK[i] <= 9) {
            printf("%d", radixK[i]);
        } else {
            printf("%c", radixK[i] - 10 + 'A');
        }
    }
    return 0;
}

总结：x进制数 转化为 y进制(s-ans-out)。
(string字符串的长度不能超过65534)(用10进制转化)

#include <bits/stdc++.h>
using namespace std;
int main(){
    string s;
    int x, y;  
    //输入二进制字符串 、 x进制字符串s 转化为 y进制字符串out
    cin>>s>>x>>y;
    //1.末位累加法：s转化为ans
    long long ans = 0;   //若ans位数超过long long范围，则需要构造大数运算
    for (int i = 0; i < int(s.size()); i++) {  
        ans = ans * x;  
        if (s[i] >= '0' && s[i] <= '9') ans += (s[i] - '0');  //如果是0-9
        else ans += (s[i] - 'A') + 10;  //如果是A-F
    }  
    //2.除基取余法：ans转化为out（逆序存入）
    string out;
    int w;
    while (ans > 0) {  
        w = (ans % y);  
        if (w < 10) out += w + '0';  //如果是0-9
        else out += (w-10) + 'A';  //如果是A-F
        ans /= y;  
    }  
    //3.倒序输出
    out.reserve();
    cout<<out<<endl;
    return 0;  
}

3.7 字符串

看清输入输出格式、边界、细节信息。

• C风格常用API：#include<cstring> ， strlen(str)：返回字符数组char[]长度。

• C++风格常用API：#include<string>，string类有很多成员函数可供调用，熟练掌握STL可以薄纱这些题目。

保存一句英文句子(无标点，单词用空格分隔)：使用string，每行保存一个句子(空格不断句，换行断句)。

//指定n行
vector<string> text;
string tmp;
int n;
cin>>n;
getchar();
for(int i=0;i<n;i++){
	getline(cin,tmp)；//读取一行句子，\n截止，getline在<string>中，可以接收第三个参数终止字符，默认为'\n'
	//getline读取一行字符时，默认遇到’\n’(自定义结束符)时终止，并且将’\n’(自定义结束符)直接从输入缓冲区中删除掉
	//gets相比，可以接收第三个参数终止字符，默认为'\n'
	text.push_back(tmp);
}    

【重点】：类似未指定个数的读取，都可以使用while(cin/getline/scanf)结构，但注意cin>>不回收\n，getline回收\n，用完cin再用getline就需要清空缓冲区里的\n：在getline(cin,line)之前添加一句：cin.ignore()。但连续的getline之间就不需要清空\n，因为getline会默认将\n删除。

//未指定行数
vector<string> text;
string tmp;
while(getline(cin,tmp)){//当读取到文件尾时，while终止
	if(tmp==终止串)break；
	text.push_back(tmp);
	在循环里面进行cin>>操作；
	cin.ignore();
}
//如int型也可以用cin实现
vector<int> arr;
int a;
while(cin>>a){
	arr.push_back(a);
}

• 字母的ASCII码：A(65)~ Z(90), a(97)~z(122)

• 需要统计字母个数时，注意Hash映射思想，a ~ z，0 ~ 23。

• 处理字符数组复杂的关系时，要有游标扫描思想(游标i，j就像指针一样对str[]进行扫描判断)

删除字符串内重复字符:

string str="aadfgggh";
//去重复
sort(str.begin(),str.end());
str.erase(unique(str.begin(),str.end()),str.end());  

删除字符串内某个指定字符:

string str="aadfgggh";
str.erase(remove(str.begin(),str.end(),'a'),str.end()); //在容器中, 删除[begin,end)之间的所有值等于'a'的值.

#include<string>
string::erase(begin,end)：删除[begin,end)之间的所有值

#include<algorithm>
remove(begin,end,val)：
可以从它的前两个正向迭代器参数指定的序列中移除和第三个参数相等的对象。基本上每个元素都是通过用它后面的元素覆盖它来实现移除的。
返回的迭代器指向通过这个操作得到的新序列的尾部，所以可以用它作为被删除序列的开始迭代器来调用 samples 的成员函数 erase()。

4. 递归与分治

递归：是程序调用自身的编程技巧。边界条件+递归方程是递归函数的两个要素。

分治：①将原问题分解为若干和原问题拥有相同或相似结构的子问题(子问题应当是相互独立、没有交叉的)。②使用递归函数求出每个局部子问题的解，③再将合并子问题的解，最终解决原问题，的编程手法。

另外，分治法作为一种算法思想，既可以使用递归的手段去实现，也可以通过非递归的手段去实现，可以视具体情况而定，一般来说，递归较容易实现。

5. 贪心

贪心思想，是追求当前局部最优解，从而得到全局最优解。贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，只做出在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。使用贪心的时候，往往需要先按照某个特性先排好序，也就是说贪心一般和sort一起使用。

解题的通用步骤
1、建立数学模型来描述问题；
2、把求解的问题分成若干个子问题；
3、对每一子问题求解，得到子问题的局部最优解；
4、把子问题的局部最优解合成原来问题的一个解。

题型总结
贪心问题在很多机试难度低的学校，可以成为压轴题。在机试难度高的学校也是中等难度及以上的题目，为什么明明贪心看起来这么容易的题目，却成为大多数学生过不去的坎呢？ 一、是很多同学根本就没有想到这个题目应该用贪心算法，没能将题目抽象成数学模型来分析，简单说就是没有读懂题目隐藏的意思。二、是读懂题了，知道应该是贪心算法解这个题目，但是排序的特征点却没有找准，因为不是所有题目都是这么明显的看出来从小到大排序，有的题目可能隐藏的更深，但是这种难度的贪心不常见。
所以机试中的贪心题，你要你反应过来这是一个贪心，99%的情况下都能解决。

6.前缀和与差分

前缀和=积分：求子序列和 或 子矩阵和。
(在连续区间以O(1)时间复杂度求子序列和)

差分=微分：通过差分序列/矩阵(改变边界+-c) 操作 前缀和序列/矩阵某一区间内的值(统一+c)。
(在连续区间以O(1)时间复杂度±一个常数)

6.1 一维前缀和

前缀和可以简单理解为高中的「数列的前 n 项的和」，是一种重要的预处理方式，能大大降低查询的时间复杂度。C++ 标准库中实现了前缀和函数 std::partial_sum，定义于头文件 #include<numeric> 中。

递推公式（i从1开始）：sum[i] = sum[i-1] + arr[i] (i>1), sum[1] = arr[1]
作用：快速求出原数组arr中[l,r]的区间和 = sum[r] - sum[l]

#include<bits/stdc++.h>
using namespace std;

const int N = 1e6+10;
int sum[N],arr[N];
int l,r,n,m;

int main(){
	cin>>n>>m;
	//0 2 1 3 6 4
	for(int i=1;i<=n;i++) cin>>arr[i];
	//0 2 3 6 12 16
	for(int i=1;i<=n;i++) sum[i] = sum[i-1]+arr[i];
	//sum[r] - sum[l-1] 
	while(cin>>l>>r) cout<<sum[r]-sum[l-1]<<endl;
    return 0;
}

6.2 二维前缀和

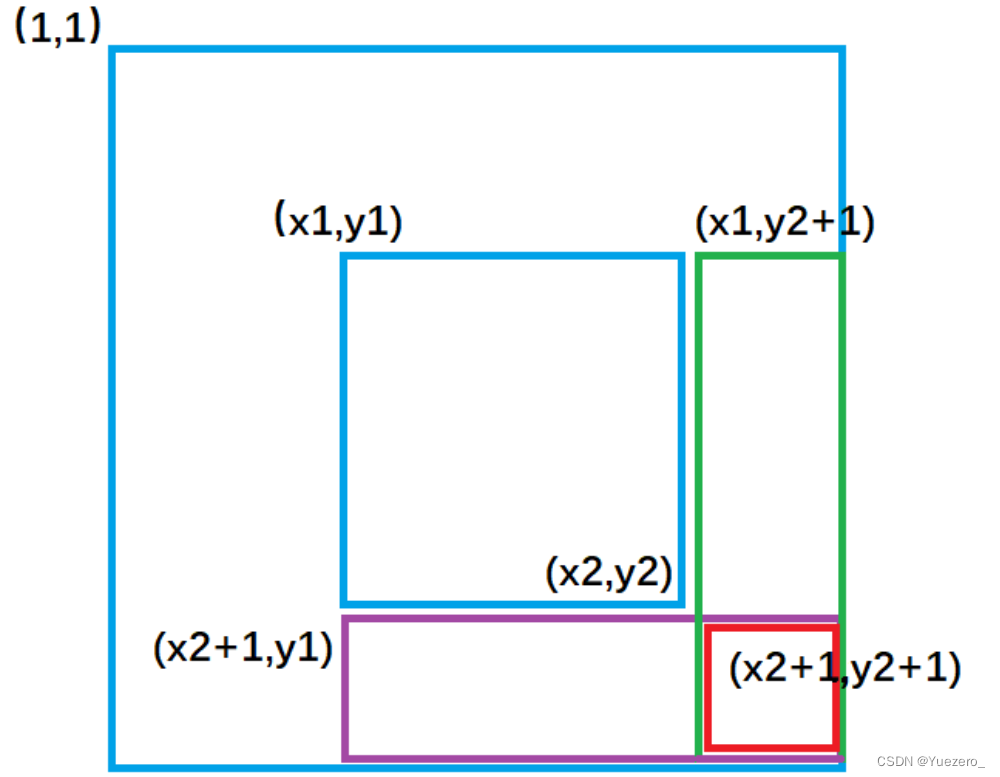
矩阵中 某点左上角区域之和 sum[i][j]（容斥原理）。
递推公式：sum[i][j] = sum[i][j-1] + sum[i-1][j] -sum[i-1][j-1] + arr[i][j]

作用：求矩阵中子矩阵和= 左上点A(x1,y1)到右下点B(x2,y2)的区域之和，A点右下角区域的和 与 B点左上角区域的和 的交, area[A][B] = sum[x2,y2] - sum[x1][y2] - sum[x2,y1] + sum[x1,y1]

• 全局变量和静态变量存储在全局数据段中
• 局部变量存储在栈上
• 动态分配的内存存储在堆上。

#include<bits/stdc++.h>
using namespace std;

const int N = 1e3+10;
int sum[N][N],arr[N][N];
int n,m,q,x;


int main(){
	cin>>n>>m>>q;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>arr[i][j];
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + arr[i][j];
	int x1,y1,x2,y2;
	while(cin>>x1>>y1>>x2>>y2){cout<<sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1] <<endl;}
    return 0;
}

6.3 一维差分

差分可以维护多次对序列的一个区间加上一个数c，并在最后询问某一位的数或是多次询问某一位的数。

b数组是a数组的差分，a数组是b数组的前缀和：a[i] = b[1]+......+ b[i]

递推公式（i从1开始）：b[i] = a[i] - a[i-1] (i>1), b[1] = a[1]

作用：如果要求a数组[l,r]区间内的所有数+=c，则需要将b[l] += c(给l后的所有前缀和a[i]加一个c)，且b[r+1] -= c(给r+1后的所有前缀和a[i]减一个c)

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5+10;
int a[N],b[N];
int n,m,l,r,c;

void insert_c(int l, int r, int c){
	b[l]+=c;
	b[r+1]-=c;
}

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i]; a[0]=0;
	for(int i=1;i<=n;i++) b[i]=a[i]-a[i-1];
	while(cin>>l>>r>>c)	insert_c(l,r,c);
	for(int i=1;i<=n;i++) b[i]+=b[i-1];//把b数组变成自己的前缀和数组
	for(int i=1;i<=n;i++) cout<<b[i]<<' '; 
    return 0;
}

6.4 二维差分

已知数组b[i][j]，它的前缀和矩阵a[i][j] = b矩阵左上角区域和。(但一般给前缀和矩阵a，递推求b，再进行a矩阵的子矩阵±c操作->转换成对b矩阵进行操作，再递推回操作后的a矩阵)

递推公式：b[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] +a[i-1][j-1]

作用：每次在子矩阵的每个元素+c（容斥原理），b[x1][y1] += c(对[x1,y1]右下区域的前缀和a都+c)，b[x2][y1] -= c(对[x2,y1]右下区域的前缀和a都-c)，b[x1][y2] -= c(对[x1,y2]右下区域的前缀和a都-c)，b[x2][y2] += c(对[x2,y2]右下区域的前缀和a都+c)

#include<bits/stdc++.h>
using namespace std;

const int N = 1e3+10;
int a[N][N],b[N][N];
int n,m,q;

void insert_c(int x1, int y1, int x2, int y2, int c){//对b数组执行插入操作，等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
	b[x1][y1]+=c;
	b[x2+1][y1]-=c;
	b[x1][y2+1]-=c;
	b[x2+1][y2+1]+=c;
}

int main(){
	cin>>n>>m>>q;
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) cin>>a[i][j];
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
	int x1,y1,x2,y2,c;
	while(cin>>x1>>y1>>x2>>y2>>c) insert_c(x1,y1,x2,y2,c);
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  //把b矩阵变成自己的前缀和矩阵a
	for(int i=1;i<=n;i++){for(int j=1;j<=m;j++) cout<<b[i][j]<<' ';cout<<endl;}
    return 0;
}

7.双指针

7.1 快慢指针

面对链表无法高效获取长度，无法根据偏移快速访问元素，是链表的两个劣势。然而面试的时候经常碰见诸如获取倒数第k个元素，获取中间位置的元素，判断链表是否存在环，判断环的长度 等（和链表长度与位置有关的问题）。这些问题都可以通过灵活运用双指针来解决。

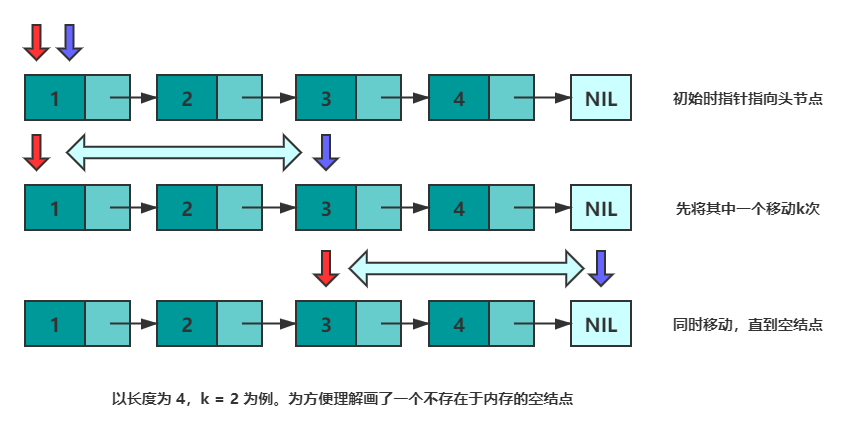
①先来看倒数第k个元素的问题(快指针fast先走k下)。设有两个指针 fast 和 slow，初始时均指向头结点。首先，先让 fast 沿着 next 移动 k 次。此时，fast 指向第 k+1个结点，slow 指向头节点，两个指针的距离为 k 。然后，同时移动 fast 和 slow，直到 fast 指向空，此时 slow 即指向倒数第 k 个结点。

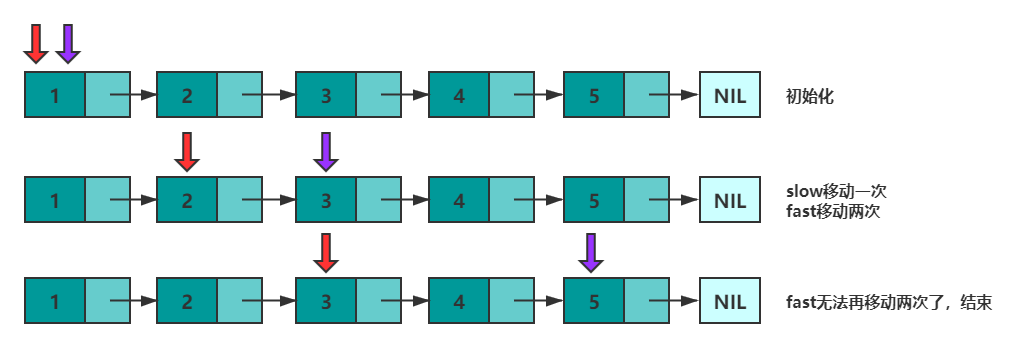
②获取中间元素的问题(快指针fast走2下，慢指针slow走1下)。设有两个指针 fast 和 slow，初始时指向头节点。每次移动时，fast向后走两次，slow向后走一次，直到 fast 无法向后走两次。这使得在每轮移动之后。fast 和 slow 的距离就会增加一。设链表有 n 个元素，那么最多移动 n/2 轮。当 n 为奇数时，slow 恰好指向中间结点，当 n 为 偶数时，slow 恰好指向中间两个结点的靠前一个(可以考虑下如何使其指向后一个结点呢？)。

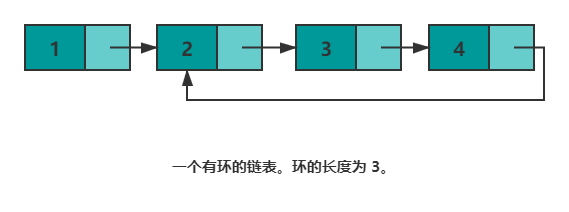
③是否存在环的问题(如果一个链表存在环，fast走2，slow走1，那么快慢指针必然会相遇。)。如果将尾结点的 next 指针指向其他任意一个结点，那么链表就存在了一个环。快慢指针的特性 —— 每轮移动之后两者的距离会加一。下面会继续用该特性解决环的问题。 当一个链表有环时，快慢指针都会陷入环中进行无限次移动，然后变成了追及问题。想象一下在操场跑步的场景，只要一直跑下去，快的总会追上慢的。当两个指针都进入环后，每轮移动使得慢指针到快指针的距离增加一，同时快指针到慢指针的距离也减少一，只要一直移动下去，快指针总会追上慢指针。

	bool hasCycle(ListNode *head) {
        ListNode* fast=head,* slow=head;
        while(fast!=NULL){
            fast = fast->next;
            if(fast!=NULL) fast = fast->next;  //如果fast没结束就再走第2步
            else return false;  //如果结束了就无循环
            slow = slow->next;
            if(slow==fast) return true;  //如果fast追上slow就有循环
        }
        return false;  //如果fast结束了就无循环
    }

④如果存在环，如何判断环的长度(fast和slow两次相遇之间的步数)。方法是，快慢指针相遇后，继续移动，直到第二次相遇。两次相遇间slow指针的移动次数即为环的长度。第一次在3相遇，开始计数，第二次还在3相遇，slow共走了3步，所以环长度为3。