AI in Finance＜量化交易&人工智能&金融投资＞(下)

7 机器学习量化策略
8 强化学习量化策略

7 机器学习量化策略

与传统策略的区别：传统策略的条件是人为设定的，机器学习的条件是从数据中学习的。

机器学习量化应用：

基于价格的分类模型（历史价格->涨跌）
基于文本的分类模型（新闻文本->选股/风控）

机器学习量化流程：

第一步：确定数据(如股票池)，划分训练集、测试集
首先我们应明确我们构建何种AI量化策略，如A股、港股还是期货等，确定数据后，接着我们把历史数据按时间顺序切分为两部分，类比于分瓜任务中的两堆瓜。
训练集：第一部分的数据用来训练模型，类比第一堆瓜；
验证集：第二部分的数据用来验证模型效果，类比第二堆瓜；

第二步：定目标：数据标注
其次我们要明确我们模型的训练目标，是预测股票收益率高低还是波动率高低，就好比是预测西瓜好坏还是年份；
在样例模板中，我们用5日收益率高低来定义股票的走势好坏等级，并将每只对应等级标记在每只股票上，类比于上述切瓜后记录每个瓜的好坏。
AI量化策略的目标(Label)：人为定义的模型预测目标，例如未来N日收益率、未来N日波动率、未来N日的收益率排序等统计量,平台AI量化策略默认使用股票收益率作为目标。
AI量化策略的标注：我们计算训练集数据所在时间阶段的每日目标值，比如按每日的未来N日收益率高低来定义股票的走势好坏等级，计算出每只股票未来N日收益率的好坏等级并标记在每只股票上。

第三步：找因子
选择构建可能影响目标的特征（量化策略中可称为因子），如模板策略中的return_5(5日收益)、return_10(10日收益)等，类比于瓜的产地、大小等特征。
AI量化策略的特征(features)：反映事物在某方面的表现或性质的事项，在AI量化策略中，特征可以是换手率、市盈率、KDJ技术指标等等

第四步：数据连接+缺失数据处理
将上述每只股票的标注数据与特征数据注意链接，以便下一步模型的学习与使用，类比于上述将每个西瓜特征与好坏一一对应；

第五步：模型训练+股票预测
我们通过“好坏等级”对股票进行标注，贴上标签，连同其所对应的特征值一起来构建训练模型，类比于上述我们获取每个瓜的特征与其对应的好坏结果，通过归纳总结找到瓜的好坏与瓜的属性之间的关联，总结出瓜的分类经验；
用验证集数据来检验训练前面构建好的模型，即检验模型根据验证集的特征数据预测出的目标值（股票走势好坏等级）是否准确。这步类比于鉴瓜任务中根据第一堆瓜总结的鉴瓜经验用第二堆西瓜的大小、颜色等特征数据来判断预测瓜的好坏。

第六步：回测
将验证集的预测结果放入历史真实数据中检测，类比于鉴瓜过程中根据第二堆瓜预测出瓜的好坏最后进行切瓜验证。

7.1 基于股价涨跌分类/回归模型

传统策略的技术因子/指标indicator = 机器学习的特征feature。

目标：基于历史数据(价格、交易量)，选择指标组合(如使用遗传算法选择)，计算指标X(features)，数据归一化normalize(x=(x-mean)/std，消除不同feature量纲的影响)，运用机器学习模型训练 $y = f (f e a t u res)$ ，预测未来大盘涨跌趋势y(回归close/二分类涨跌)
(短期预测用技术面特征，长期预测用基本面特征)。

基本技术指标features：
①Momentum动量线： mom[t] = price[t] / (price[t-n])-1
②SMA移动平均线.(smooth,laggged) 可以看作一种滤波器，反映真实价格。
③BOLL布林带:决策上下边界线是两个标准差。

常见机器学习模型用于时间序列分析：线性回归、Logistic regression、SVM、Random Forest、LSTM。

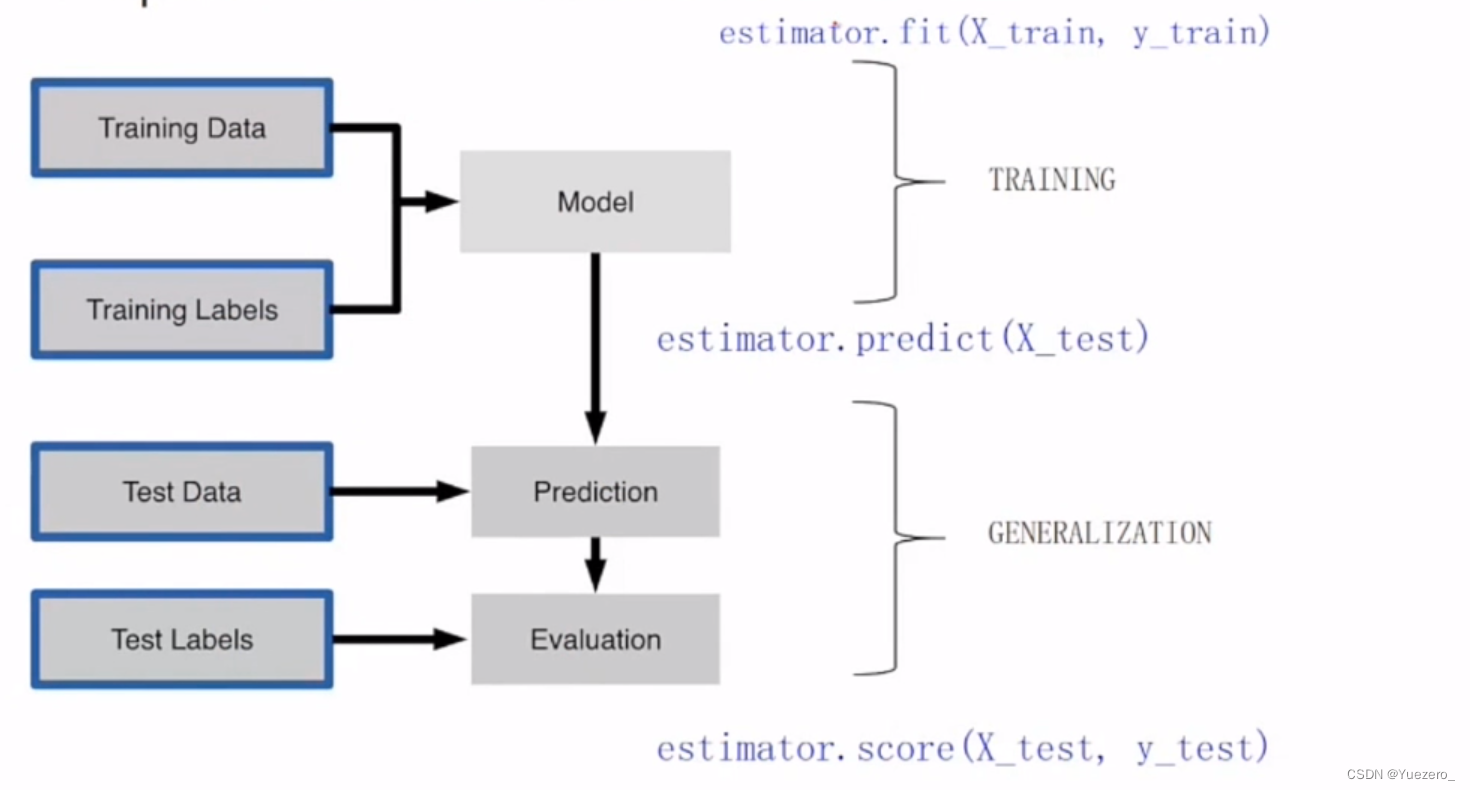
sklearn模型使用范式：
在这里插入图片描述

7.1.1 特征选择(遗传算法因子挖掘)

特征X选择与构造十分重要，一开始我们可能构造了成百上千个因子，计算特征放入df中，但哪些是真正有效的，我们无从得知。
我们可以按照公式构建自己的FeatureUtils.py，里面定义各种指标的计算函数。只需import FeatureUtils就可用使用定义好的函数计算各种指标。

特征选择本质上是一个组合优化问题[背包问题]：可用使用遗传算法进行因子挖掘解决。

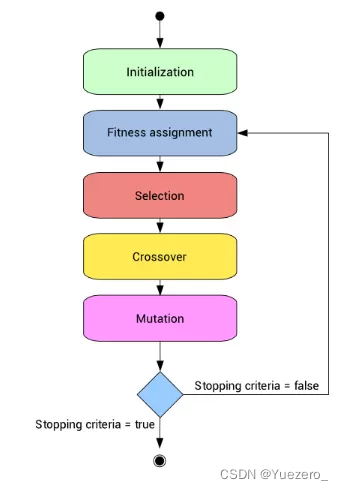
遗传算法 (Genetic Algorithms，简称GA)：
一种启发式算法，先进行定向的选择，再进行不定向的变异，根据能体现目标的适应度函数，来体现每一代个体的适应度，从而依据适应度进行选择操作，然后再进行遗传迭代，产生带有新的基因组合的个体。可用TPOT 库（树形传递优化技术）实现。
在这里插入图片描述
遗传算法因子挖掘实战：
[注]：迭代时间太短，它就不会为你的问题找出最可能传递方式。

pip install deap update_checker tqdm
pip install tpot

# import basic libraries
import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
%matplotlib inline 
from sklearn import preprocessing 
from sklearn.metrics import mean_squared_error 
# Big Mart Sales


## preprocessing
### mean imputations
# Big Mart Sales
train = pd.read_csv("./data/Train_UWu5bXk.csv")
test = pd.read_csv("./data/Test_u94Q5KV.csv")
train['Item_Weight'].fillna((train['Item_Weight'].mean()), inplace=True)
test['Item_Weight'].fillna((test['Item_Weight'].mean()), inplace=True)

# Big Mart Sales

### reducing fat content to only two categories
number = preprocessing.LabelEncoder()
# number = LabelEncoder()
train['Item_Fat_Content'] = train['Item_Fat_Content'].replace(['low fat','LF'], ['Low Fat','Low Fat'])
train['Item_Fat_Content'] = train['Item_Fat_Content'].replace(['reg'], ['Regular'])
test['Item_Fat_Content'] = test['Item_Fat_Content'].replace(['low fat','LF'], ['Low Fat','Low Fat'])
test['Item_Fat_Content'] = test['Item_Fat_Content'].replace(['reg'], ['Regular'])
train['Outlet_Establishment_Year'] = 2013 - train['Outlet_Establishment_Year']
test['Outlet_Establishment_Year'] = 2013 - test['Outlet_Establishment_Year']

train['Outlet_Size'].fillna('Small',inplace=True)
test['Outlet_Size'].fillna('Small',inplace=True)

train['Item_Visibility'] = np.sqrt(train['Item_Visibility'])
test['Item_Visibility'] = np.sqrt(test['Item_Visibility'])

col = ['Outlet_Size','Outlet_Location_Type','Outlet_Type','Item_Fat_Content']
test['Item_Outlet_Sales'] = 0
combi = train.append(test)
for i in col:
    combi = number.fit_transform(combi.astype('str'))
    combi = combi.astype('object')
train = combi[:train.shape[0]]
test = combi[train.shape[0]:]
test.drop('Item_Outlet_Sales',axis=1,inplace=True)
## removing id variables
from sklearn.model_selection import train_test_split
tpot_train = train.drop(['Outlet_Identifier','Item_Type','Item_Identifier'],axis=1)
tpot_test = test.drop(['Outlet_Identifier','Item_Type','Item_Identifier'],axis=1)
target = tpot_train['Item_Outlet_Sales']
tpot_train.drop('Item_Outlet_Sales',axis=1,inplace=True)
# finally building model using tpot library

from tpot import TPOTRegressor
X_train, X_test, y_train, y_test = train_test_split(tpot_train, target,
train_size=0.75, test_size=0.25)

tpot = TPOTRegressor(generations=5, population_size=50, verbosity=2)
tpot.fit(X_train, y_train)
print(tpot.score(X_test, y_test))
tpot.export('tpot_boston_pipeline.py')



## predicting using tpot optimised pipeline

tpot_pred = tpot.predict(tpot_test)
sub1 = pd.DataFrame(data=tpot_pred)
#sub1.index = np.arange(0, len(test)+1)
sub1 = sub1.rename(columns = {'0':'Item_Outlet_Sales'})
sub1['Item_Identifier'] = test['Item_Identifier']
sub1['Outlet_Identifier'] = test['Outlet_Identifier']
sub1.columns = ['Item_Outlet_Sales','Item_Identifier','Outlet_Identifier']
sub1 = sub1[['Item_Identifier','Outlet_Identifier','Item_Outlet_Sales']]
sub1#.to_csv('tpot.csv',index=False)

7.1.2 Linear Regression股价回归预测

①线性回归：
$y=X\theta, (\theta 是权重参数)$
$loss=J(\theta)=(y-X\theta)^T(y-X\theta)$

②Ridge回归(L2正则项)：
$y=X\theta, (\theta 是权重参数)$
$loss=J(\theta)=(y-X\theta)^T(y-X\theta)+λ\theta^T\theta$

③Lasso回归(L1正则项)：
$y=X\theta, (\theta 是权重参数)$
$loss=J(\theta)=(y-X\theta)^T(y-X\theta)+λ||\theta||$

④非线性Kernel回归(核函数)：思想同DL中的激活函数，如高斯核函数。
$y=\varphi(X\theta), (\varphi为非线性函数)$
$loss=J(\theta)=(y-\varphi(X\theta))^T(y-\varphi(X\theta)) + [λ\theta^T\theta 或 λ||\theta||]$

CrossValidation实战回归模型：
[注意]：工程中正常训练，在验证集上选择超参数，然后在测试集测试后，再把训练集和测试集一起用于训练，再去回测和实盘，不然会有数据浪费。
这里的测试并不规范！得在测试集上测试，且faetures仅用[“date”, “open”, “high”, “low”, “close”, “volume”]

from Ashare import *
from MyTT import *  # myTT麦语言工具函数指标库  https://github.com/mpquant/MyTT
import numpy as np
import pandas as pd  # 数据处理, 读取 CSV 文件
import matplotlib.pyplot as plt
# from plotly.offline import init_notebook_mode, iplot, iplot_mpl
# import plotly.graph_objs as go
from sklearn.linear_model import LinearRegression
from sklearn import preprocessing
import sklearn

# 导入数据
Stock_Code = 300015
df = get_price(f'{Stock_Code}.XSHE', frequency='1d', count=120, end_date='2023-03-06')  # 可以指定结束日期，获取历史行情
df.to_csv(f'{Stock_Code}.csv')
df = pd.read_csv(f'{Stock_Code}.csv')
df.columns = ["date", "open", "high", "low", "close", "volume"]
# 将日期的键值的类型从字符串转为日期
df['date'] = pd.to_datetime(df['date'])

CLOSE = df.close.values  # 基础数据定义，只要传入的是序列都可以  Close=df.close.values
OPEN = df.open.values   # 例如  CLOSE=list(df.close) 都是一样
HIGH = df.high.values
LOW = df.low.values
df['ma5'] = MA(CLOSE, 5)  # 获取5日均线序列
df['ma10'] = MA(CLOSE, 10)  # 获取10日均线序列
df['ma20'] = MA(CLOSE, 20)  # 获取10日均线序列
# df = df.drop(labels=np.arange(20).tolist(), axis=0)


categories = {'volume', 'ma5', 'ma10', 'ma20'}
'''数值大小尽量统一化'''
for cate in categories:
    df[cate] = abs(df[cate]-df[cate].mean()) / np.std(df[cate])
df = df.set_index('date')
# 按照时间升序排列
df.sort_values(by=['date'], inplace=True, ascending=True)
# 检测是否有缺失数据,丢弃含NaNs的行
df.dropna(axis=0, inplace=True)
# print(df.tail())

# 日期
Min_date = df.index.min()
Max_date = df.index.max()
print("First date is", Min_date)
print("Last date is", Max_date)
print(Max_date - Min_date)


# 线性回归
# 创建新的列label，, 包含预测值, 根据当前的数据预测5天以后的收盘价
date = "2023-01-17"
num = 30  # 预测date  num天后的情况
df['label'] = df['close'] # 预测值  每天的最终股票价格
# 丢弃 ‘label’, ‘price_change’, ‘p_change’, 不需要它们做预测
Data = df.drop(['label'], axis=1)
print(df.tail())
# 线性回归模型的特征/指标： open   high    low  close  ...       ma5      ma10      ma20
X = Data.values
# Standardize
X = preprocessing.scale(X)
df.dropna(inplace=True)
# 回归结果Target=label=close
Target = df.label
y = Target.values
# print(np.shape(X), np.shape(y))
'''x 特征，y 股价'''
# 将数据分为训练数据和测试数据
X_train, X_test,  y_train ,y_test= sklearn.model_selection.train_test_split(X,y,test_size=0.1,random_state=42)
lr = LinearRegression()
lr.fit(X_train, y_train)
lr.score(X_train,y_train)  # 使用绝对系数 R^2 评估模型
sc = lr.score(X_test, y_test)
print('score=',sc*100,'%')

# 做预测，最近num天的股价
# 此处使用的特征是最近num=30天的特征，而目前使用的数据是之前的特征量，由于归一化，
# 实际上若真要预测，首先要预测这些特征的值随时间变化的概率
X_Predict = X[-num:]
Forecast = lr.predict(X_Predict)
# 画预测结果
trange = pd.date_range(f'{date}', periods=num, freq='d')
# print(trange)
# 产生预测值dataframe
Predict_df = pd.DataFrame(Forecast, index=trange)
Predict_df.columns = ['forecast']

# 将预测值添加到原始dataframe
df = pd.read_csv(f'./{Stock_Code}.csv')
# print(df['date'][30:])
df.columns = ["date", "open", "high", "low", "close", "volume"]
print(df.loc[:,['date','close']].tail(30))
print(Predict_df)

# 画预测值和实际值


plt.subplot(2, 1, 1)
df.tail(30)['close'].plot(color='blue', linewidth=3)

plt.subplot(2, 1, 2)
Predict_df['forecast'].plot(color='orange', linewidth=3)
plt.xlabel('Time')
plt.ylabel('Price')
plt.legend()
plt.show()

7.1.3 Logestic Regression涨跌分类预测

7.1.4 Random Forests涨跌分类预测

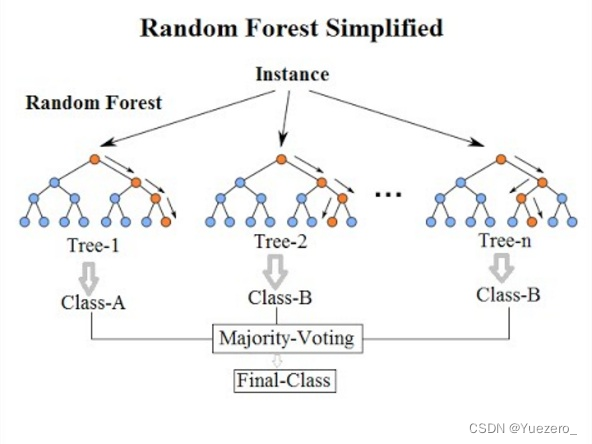
随机森林是一个包含多个决策树的分类器，每个决策树都对特征空间进行贪心划分，决策时输出的类别是由个别树输出的类别的众数而定，数模型需要大量调参。

决策树：
每个内部节点上选用一个属性进行分割
每个分叉对应一个属性值
每个叶子节点代表一个分类

集成学习：每个决策树训练时，每次在所有n个因子中随机选择 $\sqrt{n}$ 个因子进行训练，保证了每棵树学习能力的多样性。

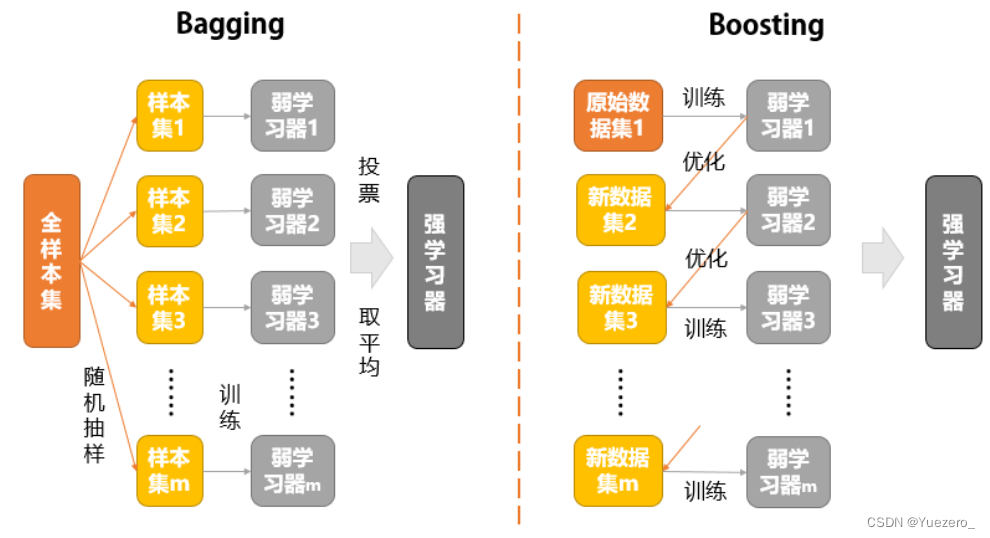
Bagging：Sklearn库(随机森林)并行训练
Boosting：XGBoost库(GDBT)串行拟合

在这里插入图片描述
Boosting和Bagging作为集成学习的两大分支，区别在于：

Bagging采用bootstrap随机抽样从整体数据集中得到很多个小数据集（小袋），用每一个小数据集分别并列训练弱学习器，最后采纳投票或者取均值的方式得到强学习器。
Boosting的想法是加强，用整体数据集训练出第一个弱学习器后，在此基础上采用调整权值或者拟合残差的方法降低数据集的损失，最后采用加权平均或者加法原理得到强学习器。Boosting每一步的优化都要在得到上一步弱学习器的基础上进行，是一种“串行”的方法。

在这里插入图片描述
随机森林二分类(涨or跌)实战：，使用集成机器学习建模解决。[‘close’, ‘volume’, ‘close-open’, ‘MA5’, ‘MA10’, ‘high-low’, ‘RSI’, ‘MOM’, ‘EMA12’, ‘MACD’, ‘MACDsignal’, ‘MACDhist’]，12个技术指标作为分类的特征，对随机森林模型进行训练。最后发现，模型中决策树个数增加，模型准确率增加并有收敛趋势；并且，预测的时间窗口越长，模型越准确。

from Ashare import *
from MyTT import *  # myTT麦语言工具函数指标库  https://github.com/mpquant/MyTT
import numpy as np  # 科学计算相关库
import pandas as pd  # 科学计算相关库
import matplotlib.pyplot as plt  # 引入绘图相关库
from sklearn.ensemble import RandomForestClassifier  # 引入分类决策树模型
from sklearn.metrics import accuracy_score  # 引入准确度评分函数
import warnings

warnings.filterwarnings("ignore")  # 忽略警告信息，警告非报错，不影响代码执行

# 1.股票基本数据获取
# 导入数据
Stock_Code = '000666'
df = get_price(f'{Stock_Code}.XSHE', frequency='1d', count=3000, end_date='2023-03-08')  # 可以指定结束日期，获取历史行情
df.to_csv(f'{Stock_Code}.csv')
df = pd.read_csv(f'{Stock_Code}.csv')
df.columns = ["date", "open", "high", "low", "close", "volume"]
# 将日期的键值的类型从字符串转为日期
df['date'] = pd.to_datetime(df['date'])
df = df.set_index('date')  # 设置日期为索引
CLOSE = df.close.values  # 基础数据定义，只要传入的是序列都可以  Close=df.close.values
OPEN = df.open.values  # 例如  CLOSE=list(df.close) 都是一样
HIGH = df.high.values
LOW = df.low.values

# 2.简单衍生特征构造
df['close-open'] = (df['close'] - df['open']) / df['open']
df['high-low'] = (df['high'] - df['low']) / df['low']

df['pre_close'] = df['close'].shift(1)  # 该列所有往下移一行形成昨日收盘价
df['price_change'] = df['close'] - df['pre_close']
df['p_change'] = (df['close'] - df['pre_close']) / df['pre_close'] * 100

# 3.移动平均线相关特征构造
df['MA5'] = MA(CLOSE, 5)  # 获取5日均线序列
df['MA10'] = MA(CLOSE, 10)  # 获取10日均线序列
df.dropna(inplace=True)  # 删除空值

# 4.通过Ta_lib库构造衍生变量
df['RSI'] = RSI(df['close'])  # 相对强弱指标
_, df['MOM'] = MTM(df['close'])  # 动量指标
df['EMA12'] = EMA(df['close'], N=12)  # 12日指数移动平均线
df['EMA26'] = EMA(df['close'], N=26)  # 26日指数移动平均线
df['MACDhist'], df['MACDsignal'], df['MACD'] = MACD(df['close'])  # MACD值
df.dropna(inplace=True)  # 删除空值

# 查看此时的df后五行
# print(df.tail())
X = df[['close', 'volume', 'close-open', 'MA5', 'MA10', 'high-low', 'RSI', 'MOM', 'EMA12', 'MACD', 'MACDsignal', 'MACDhist']]
# 涨1，跌-1
y = np.where(df['price_change'].shift(-1)> 0, 1, -1)


# 5.按照时间序列划分数据集
# 因为我们是根据当天数据来预测下一天的股价涨跌情况，而不是任意一天的股票数据来预测下一天的股价涨跌情况。
# 因此，我们将前90%的数据作为训练集，后10%的数据作为测试集
X_length = X.shape[0]  # shape属性获取X的行数和列数，shape[0]即表示行数
split = int(X_length * 0.9)

X_train, X_test = X[:split], X[split:]
y_train, y_test = y[:split], y[split:]


# 6.模型搭建
model = RandomForestClassifier(max_depth=3, n_estimators=10, min_samples_leaf=10, random_state=1)
model.fit(X_train, y_train)

# 7.预测下一天的涨跌情况
y_pred = model.predict(X_test)
print(y_pred)
a = pd.DataFrame()  # 创建一个空DataFrame
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)
print(a.tail())

# 查看预测概率
y_pred_proba = model.predict_proba(X_test)
# print(y_pred_proba[0:5])

# 模型准确度评估
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)
# 此外，我们还可以通过模型自带的score()函数记性打分，代码如下：
model.score(X_test, y_test)

# 分析不同数据因子特征的重要性
features = X.columns
importances = model.feature_importances_
a = pd.DataFrame()
a['特征'] = features
a['特征重要性'] = importances
a = a.sort_values('特征重要性', ascending=False)
print(a)

XGBoost与随机森林相比，明显的优势在于回测速度很快，这和其并行处理特征的特点相关。从回测结果来看，XGBoost策略不及随机森林，收益率比随机森林低10%，且最大回撤稍稍高出随机森林2%。当然，经过进一步调参，相信XGBoost的效果会有比较大的提升。