在大量的应用领域中,很少能直接用分析方法求得系统变量之间函数关系,一般都是
利用测得的一些分散的数据节点,运用各种拟合方法来生成一条连续的曲线。例如,我们
经常会碰到形如
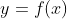 的函数。从原则上说,该函数在某个[a,b]区间上是存在的,但通
的函数。从原则上说,该函数在某个[a,b]区间上是存在的,但通
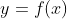 的函数。从原则上说,该函数在某个[a,b]区间上是存在的,但通
的函数。从原则上说,该函数在某个[a,b]区间上是存在的,但通
常只能获取它在
[a,b]上一系列离散节点的值,这些值构成了观测数据
。函数在其他 x
点上的取值是未知的,这时只能用一个经验函数
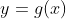 对真实函数
对真实函数
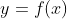 作近似。
作近似。
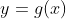 对真实函数
对真实函数
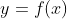 作近似。
作近似。
根据实验数据描述对象的不同,常用来确定经验函数
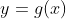 的方法有两种:插值和
的方法有两种:插值和
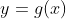 的方法有两种:插值和
的方法有两种:插值和
拟合。如果测量值是准确的,没有误差,一般用插值;如果测量值与真实值有误差,一般用曲线拟合。在 MATLAB 中,无论是插值还是拟合,都有相应的函数来处理。
项式通过全部已知的观测节点。
拟合和插值有许多相似之处,但是这两者最大的区别在于拟合要找出一个曲线方程式,
而插值仅是要求出插值数值即可。
用
MATLAB
可以很容易地实现插值和拟合,与插值有关的常用函数有:
interp1(
一维
插值
)
、
interp1q(
快速一维线性插值
)
、
interpft(
采用
FFT
法的一维插值
)
、
spline(
三次样条插
值
)
、
interp2(
二维插值
)
、
interp3(
三维插值
)
、
interpn(n
维插值
)
。
1.多项式插值函数(interp1)
yi = interp1(x,y,xi,method)
对应于插值函数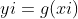
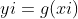
其中
x
和
y
是原已知数据的
x
、
y
值,
xi
是要内插的数据点,
method
是插值方法,可以设定的内插方法有:
‘nearest’
为寻找
最近数据节点,由其得出函数值;
‘linear’
为线性插值;
‘spline’
为样条插值函数,在数据节
点处光滑,即左导等于右导;
‘cubic’
为三次方程式插值。其中
‘nearest’
执行速度最快,输出
结果为直角转折;
‘linear’
是默认值,在样本点上斜率变化很大;
‘spline’
最花时间,但输出
结果也最平滑;
‘cubic’
最占内存,输出结果与
‘spline’
差不多。如果数据变化较大,以
‘spline’
函数内插所形成的曲线最平滑,效果最好。
线性插值也就是分段线性插值,它是将每两个相邻的节点用直线连起来,如此形成的
一条折线就是分段线性插值函数。线性内插是最简单的内插方法,但其适用范围很小;如
果原来数据的函数
f
有极大的变化,则假设其数据点之间为线性变化并不合理。而且线性
插值虽然在
n
足够大时精度也相当高,但是折线在各个节点处不光滑,即插值函数在节点
处导数不存在,从而影响了线性插值在需要光滑插值曲线
(
如机械加工等
)
的领域中的应用。
在
MATLAB
中,调用分段线性插值的语句为:
y=interp1(x0,y0,x)
,其中
x0
、
y0
为已
知的离散数据,求对应
x
的插值
y
;调用三次样条插值的语句为:
y=interp1(x0,y0,'spline')
或
y=spline(x0,y0,x)
,
x0
、
y0
、
x
和
y
的意义同上。
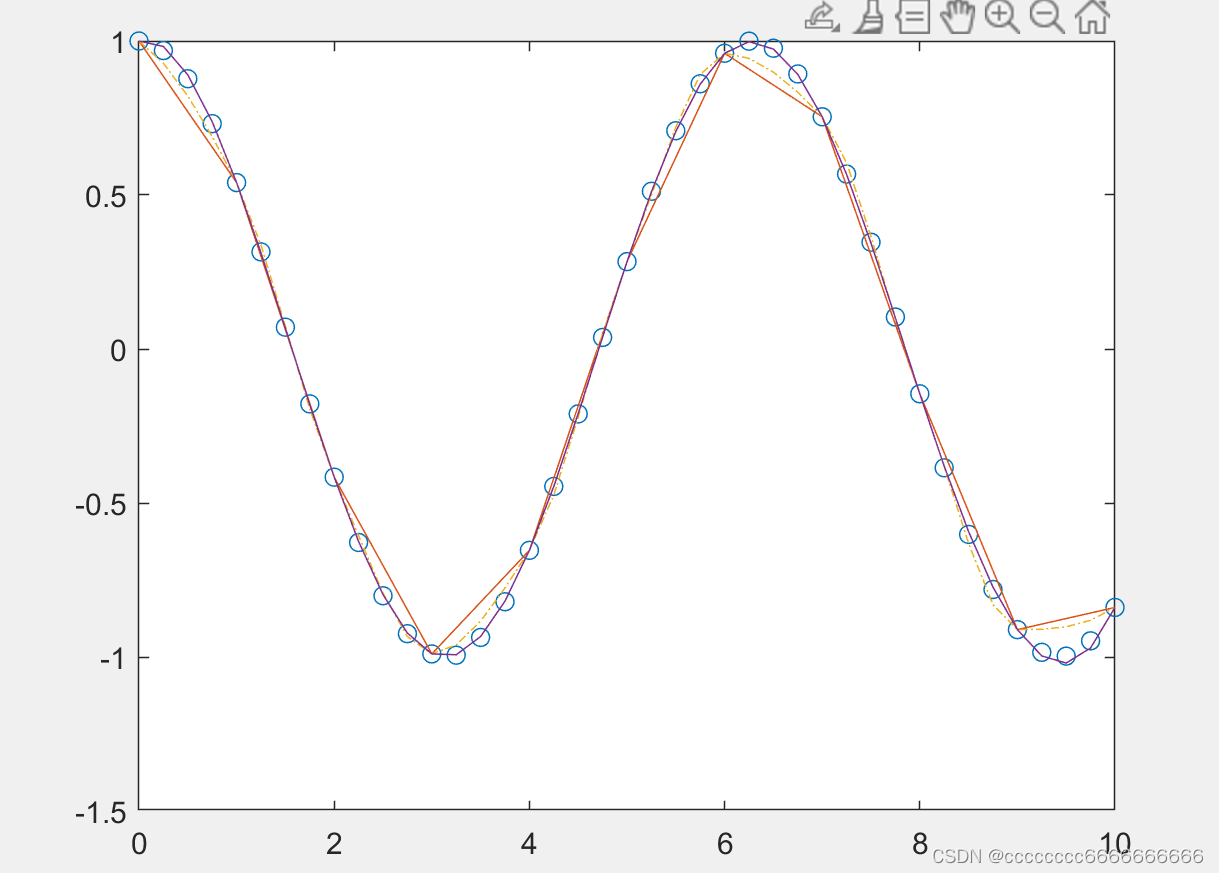
x=0:10; y=cos(x); xi=0:.25:10;
y0=cos(xi); %精确值
y1=interp1(x,y,xi); %线性插值结果
y2=interp1(x,y,xi,'pchip'); %三次方程式插值结果
y3=interp1(x,y,xi,'spline'); %样条插值结果
plot(xi,y0,'o',xi,y1,xi,y2,'-.',xi,y3)注意:书上的和现版本不同,在以后的版本中将会更改 INTERP1(...,'CUBIC')。请改用 INTERP1(...,'PCHIP')。
2.多项式拟合函数 polyfit
MATLAB
的
polyfit
函数提供了从一阶到高阶多项式的拟合,其调用方法有两种
p=polyfit(x,y,n)
[p,s]=polyfit(x,y,n)
其中
x,y
为已知的数据组,
n
为要拟合的多项式的阶次,向量
p
为返回的要拟合的多项
式的系数,向量
s
为调用函数
polyval
获得的错误预估计值。一般来说,多项式拟合中阶数
n
越大,拟合的精度就越高
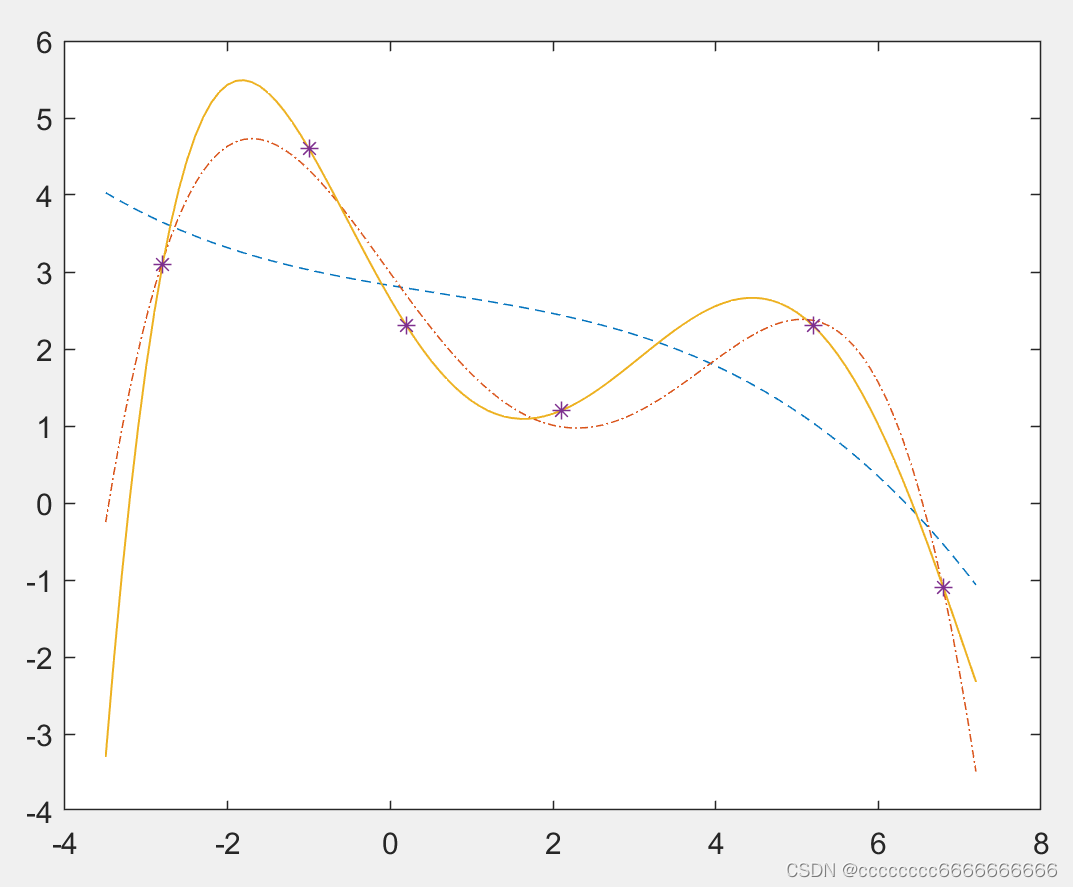
x=[-2.8 -1 0.2 2.1 5.2 6.8];
y=[3.1 4.6 2.3 1.2 2.3 -1.1];
p3=polyfit(x, y, 3); % 用不同阶数的多项式拟合 x 和 y
p4=polyfit(x, y, 4);
p5=polyfit(x, y, 5);
xcurve= -3.5:0.1:7.2; % 生成 x 值
p3curve=polyval(p3, xcurve); % 计算在这些 x 点的多项式值
p4curve=polyval(p4, xcurve);
p5curve=polyval(p5, xcurve);
plot(xcurve,p3curve,'--',xcurve,p4curve,'-.',xcurve,p5curve,'-',x,y,'*');最小二乘法拟合
我们常说的最小二乘拟合通常指最小二乘多项式拟合。比多项式更一般的拟合函数形式为
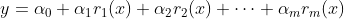
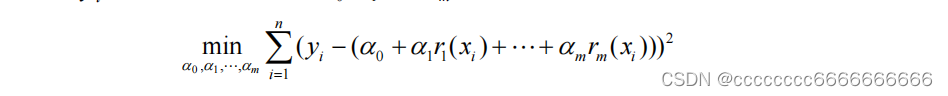
这种使
y
i
与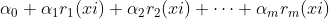 的误差平方和在最小二乘意义下最小所确定的 函数 y
称为最小二乘拟合函数。
的误差平方和在最小二乘意义下最小所确定的 函数 y
称为最小二乘拟合函数。
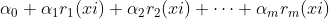 的误差平方和在最小二乘意义下最小所确定的 函数 y
称为最小二乘拟合函数。
的误差平方和在最小二乘意义下最小所确定的 函数 y
称为最小二乘拟合函数。
如果定义的拟合模型是关于参数
α
k
的线性函数,则称为线性模型;如果拟合模型关于
参数
α
k
是非线性函数,则称为非线性模型。在多数情况下,可以通过函数变换的方式将非
线性模型转化为线性模型。例如:假设拟合模型为
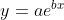 其中
a
,
b
为待定参数,是一个
其中
a
,
b
为待定参数,是一个
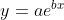 其中
a
,
b
为待定参数,是一个
其中
a
,
b
为待定参数,是一个
非线性模型。这时可对模型取对数
(
也可取常用对数
)
,得到
ln
y
=
ln
a
+
bx
,令
Y
=
ln
y
,
A
=
ln
a
,则模型转化为
Y
=
A
+
bx
,即变成一个线性模型。这样就可以利用
MATLAB
中的
polyfit
函数进行拟合计算。

x=[3 6 9 12 15 18 21 24];
y=[1.7604 1.6222 1.4914 1.3560 1.2201 1.0864 0.9494 0.8129];
%这里的 y 值是对原始 y 值求对数后得出的 Y 值
p1=polyfit(x,y,1)
b=p1(1)/0.4343
a=10.^p1(2);
y1=polyval(p1,x); %拟合值
结果也是有点奇怪,a在命令行窗口中不存在,但是可以在工具栏看到