235. 二叉搜索树的最近公共祖先

点此跳转题目链接

题目描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

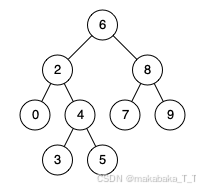
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

题解

这题是 236. 二叉树的最近公共祖先 的特殊情况，所以也可以采取通用解法：

TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
{
    // 基于后序遍历
    if (!root)
        return nullptr;
    if (root == p || root == q)
        return root;

    TreeNode *left = lowestCommonAncestor(root->left, p, q);   // 左
    TreeNode *right = lowestCommonAncestor(root->right, p, q); // 右

    // 中
    if (left && !right)
        return left;
    if (!left && right)
        return right;
    if (left && right)
        return root;
    else // 左右孩子都为空
        return nullptr;
}

但是这样就没有利用二叉搜索树的性质特点了。由于二叉搜索树是有序的，我们可以发现：

从根节点开始搜索，第一次出现值处于 $[p,q]$ 区间的节点，就是 p 和 q 的最近公共祖先。

此处不失一般性，假设 $p<q$ ，下同

以下图为例：

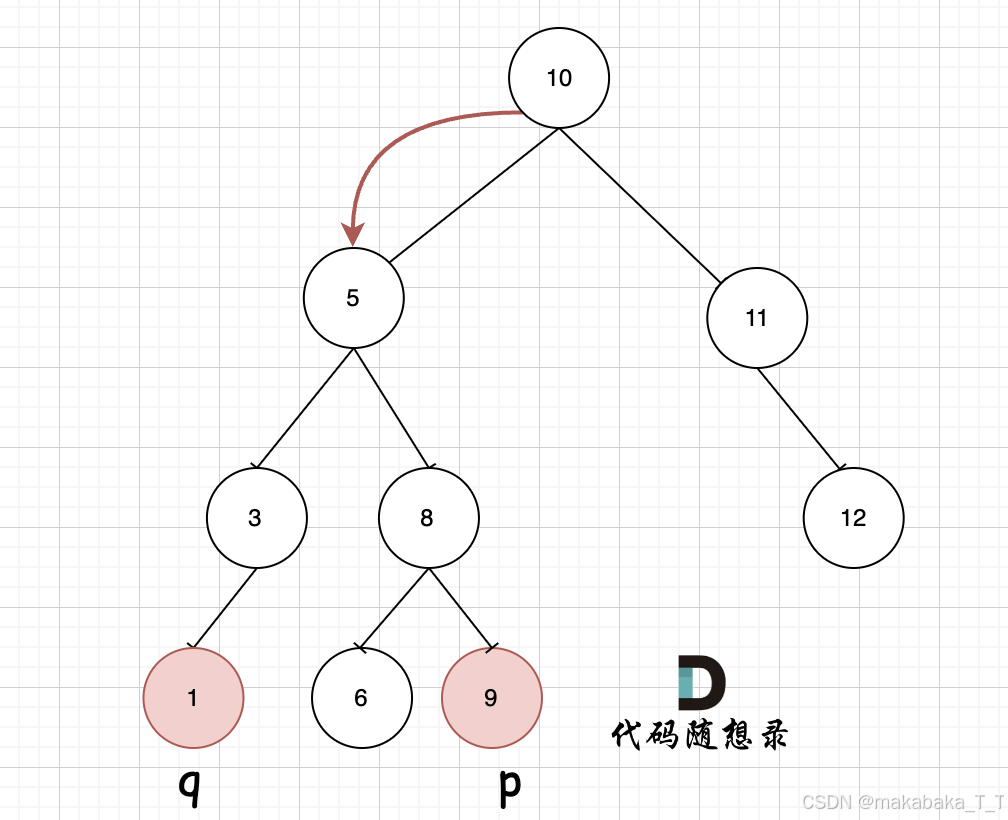
图片来源：代码随想录

可以看到，节点 5 是第一次出现在目标区间 $[1,9]$ 中的节点。此时，

• 如果再向左搜索 q ，就必然错过 p
• 如果再向右搜索 p ，就必然错过 q

所以， 5 就是它们的最近公共节点了。利用这一性质，我们可以直接采用层序遍历，找到第一个处于 $[p,q]$ 区间的节点即可：

TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
{
    // 层序遍历，第一次遇到p，q节点值区间内的节点即为它们的最近公共祖先
    queue<TreeNode*> que;
    que.push(root); // 题目确定了树不为空
    int big = p->val > q->val ? p->val : q->val;
    int small = p->val > q->val ? q->val : p->val;
    while (!que.empty()) {
        int size = que.size();
        for (int i = 0; i < size; ++i) {
            if (que.front()->val >= small && que.front()->val <= big)
                return que.front();
            if (que.front()->left)
                que.push(que.front()->left);
            if (que.front()->right)
                que.push(que.front()->right);
            que.pop();
        }
    }
    return nullptr;
}

701. 二叉搜索树中的插入操作

点此跳转题目链接

题目描述

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

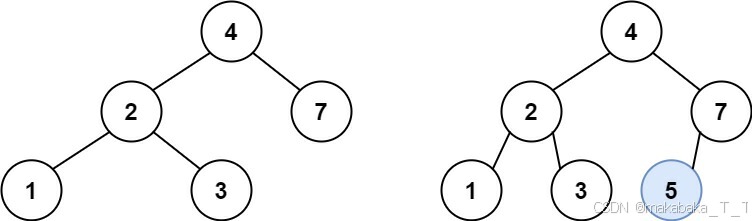
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

• 树中的节点数将在 [0, 104]的范围内。
• -108 <= Node.val <= 108
• 所有值 Node.val 是 独一无二 的。
• -108 <= val <= 108
• 保证 val 在原始BST中不存在。

题解

最简单直接的方法显然是将新节点作为叶子节点插入：从根节点开始搜索，直到空节点，然后将该空节点替换为待插入节点即可。

TreeNode *insertIntoBST(TreeNode *root, int val)
{
    // 在叶子节点插入
    if (!root)
        return new TreeNode(val);
    TreeNode *cur = root;
    TreeNode *pre;
    while (cur) {
        pre = cur;
        if (val < cur->val)
            cur = cur->left;
        else
            cur = cur->right;
    }
    if (val < pre->val)
        pre->left = new TreeNode(val);
    else 
        pre->right = new TreeNode(val);
    return root;
}

看了下官方题解也是如此，不知道为啥把这个简单题标记为“中等”难度 🤔 ​

450. 删除二叉搜索树中的节点

点此跳转题目链接

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

题解

为了深入理解删除节点的方法，我们用迭代法解决，需要考虑清楚各种情况，然后分类讨论。对于要删除的节点 d ，存在以下三种情况：

1️⃣ d 是叶子节点

2️⃣ d 只有单侧子树（左右孩子有且仅有一个不为空）

3️⃣ d 的左右孩子都不为空

前两种情况比较简单。 当 d 是叶子节点时 ，显然，直接将其删除即可：

if (!d->left && !d->right)
{
    if (d->val < pre->val) // 待删除节点是其父节点的左孩子
        pre->left = nullptr;
    else // 待删除节点是其父节点的右孩子
        pre->right = nullptr;
}

当 d 只有单侧子树时 ，将 d 替换成不为空的那个孩子节点即可：

else if (d->left && !d->right)
{
    if (d->val < pre->val)
        pre->left = d->left;
    else
        pre->right = d->left;
}
else if (!d->left && d->right)
{
    if (d->val < pre->val)
        pre->left = d->right;
    else
        pre->right = d->right;
}

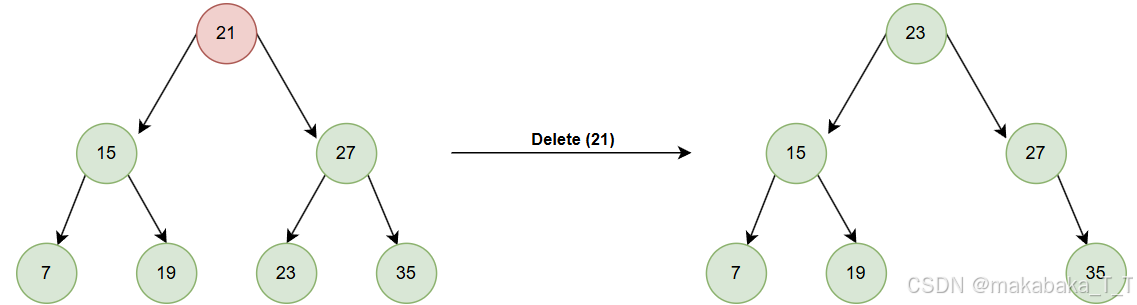
第三种情况——当 d 的左右孩子都不为空时，就比较复杂了。我采取的方法是：将 d 替换为其右子树中的最小节点（最左下节点）。下面证明一下这么做的正确性。

记 d 的节点值为 $v_d$ ， d 的左子树节点值的集合为 $\mathbf{L}$ ， d 的右子树节点值集合为 $\mathbf{R}$ 。根据二叉树的性质，

$$\begin{gathered} \forall v_l\in \mathbf{L}:v_l<v_d \\ \forall v_r\in \mathbf{R}:v_r>v_d \\ 即v_l<v_r \end{gathered}$$

现取出右子树的最小节点，即 $\mathbf{R}$ 中的最小值 v r ′ = m i n { v r } v_r' = min\{v_r\} vr′​=min{vr​} ，则

$$\begin{gathered} \forall v_r\in \mathbf{R}-v_r^{\prime }:v_r^{\prime }<v_r \\ 因为v_r^{\prime }\in \mathbf{R},所以\forall v_l\in \mathbf{L}:v_l<v_r^{\prime } \\ 所以v_l<v_r^{\prime }<v_r \\ 所以v_r^{\prime }可以替代v_d的位置 \end{gathered}$$
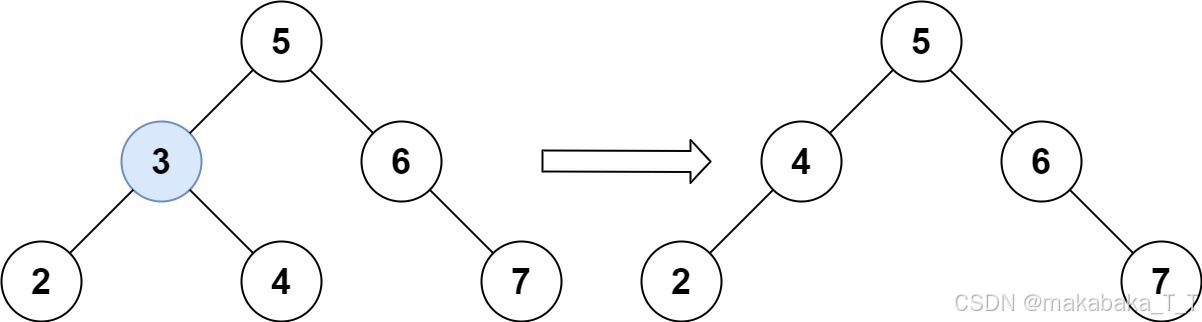
结合下面的示例图可以更好理解：

图片来源：二叉搜索树删除 | D栈 - Delft Stack

简而言之： d 右子树的最小值，大于 d 左子树中所有值、小于 d 右子树中除了它本身的所有值，故可以替代 d ，成为 d 的左右子树的新根节点。

同理，也可以用左子树的最大节点来替换待删除节点

这部分的代码实现如下：

// 找到待删除节点右孩子的最左下节点（右子树中的最小节点）
TreeNode *mostLeft = d->right;
// 特殊情况：待删除节点的右孩子无左孩子（自身就是最小节点）
if (!mostLeft->left)
{
    if (!mostLeft->right)
        d->right = nullptr;
    else
        d->right = mostLeft->right;
}
else
{
    TreeNode *preMostLeft = d; // 最左节点的父节点
    while (mostLeft->left)
    {
        preMostLeft = mostLeft;
        mostLeft = mostLeft->left;
    }
    // 将最左节点从原来的位置移除
    if (mostLeft->right)
        preMostLeft->left = mostLeft->right;
    else
        preMostLeft->left = nullptr;
}
// 将待删除节点替换为该最左节点
mostLeft->left = d->left;
mostLeft->right = d->right;
if (d->val < pre->val)
    pre->left = mostLeft;
else
    pre->right = mostLeft;

综上所述，迭代法的整体代码实现如下：

TreeNode *deleteNode(TreeNode *root, int key)
{
    TreeNode *d = root; // 待删除节点d
    TreeNode *pre = new TreeNode(INT_MAX, d, nullptr);
    TreeNode *dummyRoot = pre; // 虚拟根节点
    while (d)
    {
        if (d->val == key)
            break;
        pre = d;
        if (key < d->val)
            d = d->left;
        else
            d = d->right;
    }
    if (!d) // 没找到要删除的节点
        return root;
    else
    {
        // 待删除节点是叶子节点的情况
        if (!d->left && !d->right)
        {
            if (d->val < pre->val) // 待删除节点是其父节点的左孩子
                pre->left = nullptr;
            else // 待删除节点是其父节点的右孩子
                pre->right = nullptr;
        }
        // 待删除节点只有单侧子树的情况
        else if (d->left && !d->right)
        {
            if (d->val < pre->val)
                pre->left = d->left;
            else
                pre->right = d->left;
        }
        else if (!d->left && d->right)
        {
            if (d->val < pre->val)
                pre->left = d->right;
            else
                pre->right = d->right;
        }
        // 待删除节点左右孩子都不为空
        else
        {
            // 找到待删除节点右孩子的最左下节点（右子树中的最小节点）
            TreeNode *mostLeft = d->right;
            // 特殊情况：待删除节点的右孩子无左孩子（自身就是最小节点）
            if (!mostLeft->left)
            {
                if (!mostLeft->right)
                    d->right = nullptr;
                else
                    d->right = mostLeft->right;
            }
            else
            {
                TreeNode *preMostLeft = d; // 最左节点的父节点
                while (mostLeft->left)
                {
                    preMostLeft = mostLeft;
                    mostLeft = mostLeft->left;
                }
                // 将最左节点从原来的位置移除
                if (mostLeft->right)
                    preMostLeft->left = mostLeft->right;
                else
                    preMostLeft->left = nullptr;
            }
            // 将待删除节点替换为该最左节点
            mostLeft->left = d->left;
            mostLeft->right = d->right;
            if (d->val < pre->val)
                pre->left = mostLeft;
            else
                pre->right = mostLeft;
        }
        delete d; // 释放删除节点的空间
    }
    return dummyRoot->left;
}

可以看出，该算法从根节点起，仅向下搜索一次即可完成删除，满足题目进阶要求的 $O(h)$ 时间复杂度， $h$ 为树的高度。

同时，该算法处理待删除节点左右子树均不为空的情况时，虽然相对复杂，但是删除节点后树的高度和结构基本不会变化（最多减少一层，可以从上面的示例图看出），可以维护二叉搜索树的搜索效率（因为搜索删除节点附近的节点时，路径基本不变）。

代码随想录 中Carl的处理方法是 将待删除节点的左子树，连接到右子树的最左下节点的左孩子处，然后用该右子树替代已删除节点 。这样的代码会简单一些，也便于递归实现，但是存在每次删除节点都可能增加树的高度、降低搜索效率的问题。