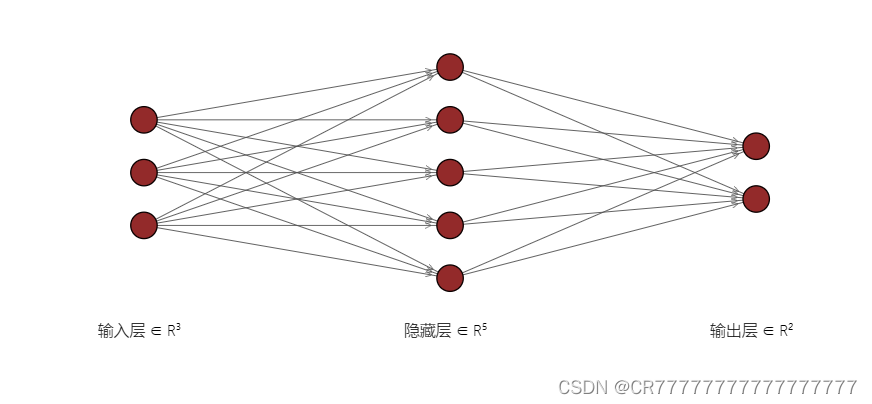
前馈神经网络(Feedforward Neural Network)是一种最基本的人工神经网络模型。它也被称为多层感知器(Multilayer Perceptron,MLP)。
在前馈神经网络中,信息只能在输入层向前传递到输出层,不存在反馈连接。网络的信息流是单向的,从输入层经过一系列的隐藏层,最终到达输出层。每个神经元都连接到下一层的所有神经元(当然这是最开始的情况,后面出现了可以dropout的连接),但不与同一层的其他神经元相连接。
前馈神经网络的基本组成单位是神经元(neuron),也称为节点(node)或单元(unit)。每个神经元都有一个或多个输入和一个输出。输入通过与权重相乘并经过激活函数处理后传递给输出。权重决定了输入对神经元的影响程度,激活函数则将输出映射到特定的范围内。
前馈神经网络通常通过训练来学习数据的模式和特征。这一过程中,网络的权重被调整以最小化输出与期望输出之间的误差。训练方法包括反向传播算法(Backpropagation)等,用于更新前向传播中参数的更新。
前馈神经网络在机器学习和深度学习中得到广泛应用,用于解决分类、回归、模式识别等问题。它的简单结构和可扩展性使得它成为许多复杂神经网络模型的基础,如卷积神经网络(Convolutional Neural Network)和循环神经网络(Recurrent Neural Network)。
1.上来直接贴代码,这是我定义的一个神经网络,很简单,一个输入层,一个全连接层,一个relu函数激活层,再接一个全连接输出层,直接输出特征得分,当然这个score不一定正确,因为没有经过反向传播网络的权重更新过程,仅作为一次前向传播的示例。
import torch
import torch.nn as nn
# 定义神经网络类
class NeuralNetwork(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(NeuralNetwork, self).__init__()
# 定义网络的层
self.fc1 = nn.Linear(input_size, hidden_size,bias=False) #3→5
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size,bias=False) #5→2
def forward(self, x):
print('输入的数据',x)
out = self.fc1(x)
print("全连接层1的输出值:", out)
out1 = self.relu(out)
print("relu层的输出值:", out1)
out2 = self.fc2(out1)
print("全连接层2的输出值:", out2)
return out2
# 创建神经网络实例
input_size = 3
hidden_size = 5
output_size = 2
model = NeuralNetwork(input_size, hidden_size, output_size)
# 定义输入数据
input_data = torch.randn(1, input_size)
print('输入数据',input_data)
argument1_weight=model.fc1.weight
argument2_weight=model.fc2.weight
argument1_bias=model.fc1.bias
argument2_bias=model.fc2.bias
print('全连接层1-nn.linear的权重参数:',argument1_weight)
print('全连接层2-nn.linear的权重参数:',argument2_weight)
print('全连接层1-nn.linear的偏置参数:',argument1_bias)
print('全连接层2-nn.linear的偏置参数:',argument2_bias)
# 前向传播
output = model(input_data)
print('最终输出值',output)2.讲解Class类
# 定义神经网络类
class NeuralNetwork(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(NeuralNetwork, self).__init__()
# 定义网络的层
self.fc1 = nn.Linear(input_size, hidden_size,bias=True) #3*5
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size,bias=True) #5*2
def forward(self, x):
print('输入的数据',x)
out = self.fc1(x)
print("全连接层1的输出值:", out)
out1 = self.relu(out)
print("relu层的输出值:", out1)
out2 = self.fc2(out1)
print("全连接层2的输出值:", out2)
return out2该类继承自torch库中的nn.Module类,其中魔法方法 __init__用于初始化网络的层(输入层,隐藏层,输出层),super(NeuralNetwork, self).__init__()作用是调用父类的nn.Module的构造函数,以确保神经网络正确继承父类的属性和方法,同时也避免了钻石继承的问题。
此初始函数定义了三个层,self.fc1是线性变换层,使用nn.Linear对输入的数据进行线性变化,nn.Linear是 PyTorch 中的一个类,用于创建一个线性变换(linear transformation)。它表示一个全连接层,将输入张量与权重矩阵相乘(内积,即相同位置点乘),然后加上偏置向量。nn.Linear的输入为特征的数量,输出也为特征的数量,这个特征的数量在神经网络中以神经元的数量来表示,当然这两个数量可以不一样。
# 创建神经网络实例
input_size = 3
hidden_size = 5
output_size = 2比如在我的这个示例中,输入数据是一个样本(batch),具有3个特征,这三个特征可以用动物来举例,比如动物需要有眼睛,鼻子,嘴巴,心脏等……才能确定它是一个动物(当然有些动物也不一定拥有这些特征),因此具体是什么动物,就要看最后输出层(output层)的特征样本了。在这里我定义的input_size为3(在神经网络中用三个神经元表示),第一个nn.Linear线性变化层将这输入的3个特征变换成了5个特征(为什么是5个特征呢,因为hidden_size层神经元有5个,我已经定义好了),这里我使用torch.randn随机定义了三个个特征值。
那肯定有人会问,为什么隐藏层(hidden_size)的特征(神经元)不是2个,10个,30个,100个,因为过多的隐藏层会引入更多的参数和非线性变换,增大隐藏层的数量会造成网络的复杂性,增加计算机的计算量。虽然有可能使得网络可以更好的拟合训练数据,避免泛化,但是太多的隐藏层也有可能造成过拟合现象,从而导致在训练数据上表现的很好,但是在测试集上表现较差。较少的隐藏层的缺点就很明显了,虽然没有引入很多参数,但是轻量化计算的网络,很容易造成检测过于泛化的现象。因此,选择隐藏层大小时需要考虑训练数据的复杂性、样本数量和计算资源等因素。如果训练数据较少或者趋势简单,增加隐藏层的大小可能不会带来明显的好处,反而可能增加过拟合的风险。如果训练数据较多或者问题比较复杂,增加隐藏层的大小可能有助于提高模型的性能。(这一段是补充,与原文没有太多关系)
言归正传,创建NeuralNetwork类的实例,命名为model,你也可以命名为其他都可以,自己认识即可。
model = NeuralNetwork(input_size, hidden_size, output_size)创建特征输入的特征数据,这里是tensor格式的数据,这里torch.randn(1,input_size)中的1就是这的上文中的一个样本,即一个动物,input_size在前文定义为了3,即输入的十个特征。
# 定义输入数据
input_data = torch.randn(1, input_size)
print('输入数据',input_data)系统随机生成的输入数据如下
输入数据 tensor([[ 1.9422, 1.7758, -0.7594]]) 输入的数据在这一层通过nn.Linear进行线性变换,nn.Linear会根据你输入的数据随机生成权重参数和偏置参数,这里我为了方便读者理解和计算就没有引入偏置参数,这个线性变换就很像大家初中学的一次函数,kx+b,k就是权重参数,b就是偏置参数,x就是你输出的特征,这里输入的是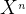
self.fc1 = nn.Linear(input_size, hidden_size,bias=True) #3*5这里为了直观理解,我这里使用下面代码可视化了self.fc1=nn.Linear的偏置参数
argument1_weight=model.fc1.weight
argument2_weight=model.fc2.weight
print('全连接层1-nn.linear的权重参数:',argument1_weight)
print('全连接层2-nn.linear的权重参数:',argument2_weight)全连接层1-nn.linear的权重参数: Parameter containing:
tensor([[ 0.1705, -0.4163, -0.4241],
[ 0.2933, -0.2816, -0.0617],
[ 0.1904, -0.3508, -0.0984],
[ 0.3392, -0.1995, 0.4307],
[ 0.2553, 0.3612, -0.4327]], requires_grad=True)
全连接层2-nn.linear的权重参数: Parameter containing:
tensor([[-0.3870, -0.2549, -0.4185, 0.3972, 0.2011],
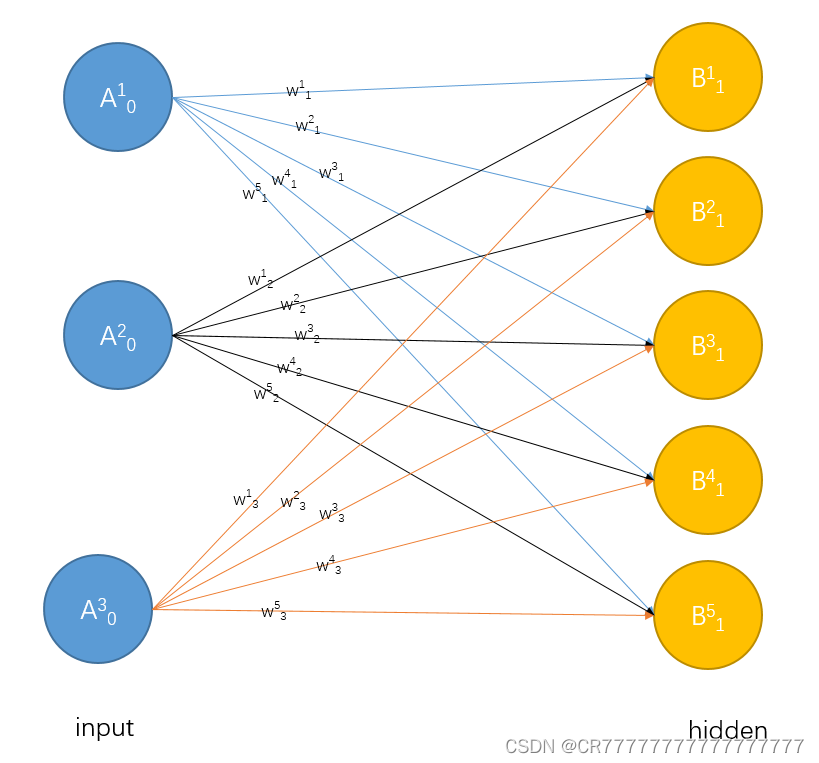
[ 0.1088, -0.0173, 0.1252, 0.0926, 0.1368]], requires_grad=True) 这是我画的全连接结构示意图,每一根连接线就是一个权重参数(因为我前文代码没有设置偏置参数),每一个输入层(input_size)的特征都会和隐藏层(hidden_size)相连接。
但是会有同学想问了,命名nn.Linear不是(输入3行,输出5列)吗,而看到上面代码中nn.Linear生成了的权重参数却是5行×3列的,这是因为torch.nn.Linear(3,5)建立了一个输入特征为 3 个分量的向量,输出特征为 5 个分量的向量的 nn.Linear 对象。我们可以用程序print检验一下这个权重参数矩阵的shape。
import torch
weight_tensor = torch.tensor([[ 0.1705, -0.4163, -0.4241],
[ 0.2933, -0.2816, -0.0617],
[ 0.1904, -0.3508, -0.0984],
[ 0.3392, -0.1995, 0.4307],
[ 0.2553, 0.3612, -0.4327]])
print(weight_tensor.shape)结果是
torch.Size([5, 3])因为输入数据是1*3格式的,但是根据矩阵乘法原理,1*3和5*3的矩阵是不能相乘的,这里我想了很久,然后画了下面示意图来思考
根据如下示意图可以理解一下
该式用矩阵形式表示
参数矩阵W就是指的全连接层FC1矩阵。
input_size和hidden_size分别是3和5,这是因为后面每一个神经元都要接受前面一层每个神经元的传过来的输入,即
再看每个参数W的排列,是不是五行×三列,这样就一目了然啦,这就是为什么在nn.Linear生成参数矩阵的时候会生成五行三列的参数矩阵,同时解答了我的疑惑,这样相乘就解答了为什么会生成5*3的参数矩阵了。
self.fc1 = nn.Linear(input_size, hidden_size,bias=False)
out = self.fc1(x)后来我仔细看了一下官方对nn.Linear类的解析。下面贴出源代码
class Linear(Module):
r"""Applies a linear transformation to the incoming data: :math:`y = xA^T + b`
This module supports :ref:`TensorFloat32<tf32_on_ampere>`.
Args:
in_features: size of each input sample
out_features: size of each output sample
bias: If set to ``False``, the layer will not learn an additive bias.
Default: ``True``
Shape:
- Input: :math:`(*, H_{in})` where :math:`*` means any number of
dimensions including none and :math:`H_{in} = \text{in\_features}`.
- Output: :math:`(*, H_{out})` where all but the last dimension
are the same shape as the input and :math:`H_{out} = \text{out\_features}`.
Attributes:
weight: the learnable weights of the module of shape
:math:`(\text{out\_features}, \text{in\_features})`. The values are
initialized from :math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})`, where
:math:`k = \frac{1}{\text{in\_features}}`
bias: the learnable bias of the module of shape :math:`(\text{out\_features})`.
If :attr:`bias` is ``True``, the values are initialized from
:math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})` where
:math:`k = \frac{1}{\text{in\_features}}`
Examples::
>>> m = nn.Linear(20, 30)
>>> input = torch.randn(128, 20)
>>> output = m(input)
>>> print(output.size())
torch.Size([128, 30])
"""
__constants__ = ['in_features', 'out_features']
in_features: int
out_features: int
weight: Tensor
def __init__(self, in_features: int, out_features: int, bias: bool = True,
device=None, dtype=None) -> None:
factory_kwargs = {'device': device, 'dtype': dtype}
super(Linear, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.empty((out_features, in_features), **factory_kwargs))
if bias:
self.bias = Parameter(torch.empty(out_features, **factory_kwargs))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self) -> None:
# Setting a=sqrt(5) in kaiming_uniform is the same as initializing with
# uniform(-1/sqrt(in_features), 1/sqrt(in_features)). For details, see
# https://github.com/pytorch/pytorch/issues/57109
init.kaiming_uniform_(self.weight, a=math.sqrt(5))
if self.bias is not None:
fan_in, _ = init._calculate_fan_in_and_fan_out(self.weight)
bound = 1 / math.sqrt(fan_in) if fan_in > 0 else 0
init.uniform_(self.bias, -bound, bound)
def forward(self, input: Tensor) -> Tensor:
return F.linear(input, self.weight, self.bias)
def extra_repr(self) -> str:
return 'in_features={}, out_features={}, bias={}'.format(
self.in_features, self.out_features, self.bias is not None
)他在第一行就说了
y = xA^T + b
这里的x就是输入数据,A是参数矩阵,^T就是转置!原来还需要转置一下,这和我推算的结果一样,只不过我在这里没有添加偏置b了。
因此全连接层的偏置由我的代码中这两句体现
argument1_bias=model.fc1.bias
argument2_bias=model.fc2.bias
输出
全连接层1-nn.linear的偏置参数: None
全连接层2-nn.linear的偏置参数: None接下来就是relu函数激活层,他把第一个全连接层的输出进行了非线性变换,第一个全连接层的输出如下。
全连接层1的输出值: tensor([[-0.0862, 0.1165, -0.1784, -0.0227, 1.4657]], grad_fn=<MmBackward0>)ReLU函数的作用是将输入值小于零的部分设置为零,而大于零的部分保持不变。换句话说,对于负数输入,ReLU函数输出为零;对于非负数输入,ReLU函数输出等于输入本身。ReLU函数在神经网络中起到引入非线性、增强表示能力、缓解梯度消失、提高计算效率等作用,被广泛应用于深度学习领域。
ReLU函数的主要作用有以下几个方面:
-
非线性映射: ReLU函数能够引入非线性映射,使神经网络能够学习更加复杂的函数关系。线性变换的叠加仍然是线性的,而ReLU函数能够在网络中引入非线性性质,使其能够学习更加复杂的模式和特征。
-
稀疏激活性: 由于ReLU函数对负数输入输出为零,它具有稀疏激活性的特点。这意味着在网络中,只有一部分神经元会被激活,而其他神经元的输出为零。这种稀疏激活性可以增加网络的表示能力,并有助于减少过拟合。
-
解决梯度消失问题: 在深层神经网络中,梯度消失是一个常见的问题。通过使用ReLU作为激活函数,它能够在反向传播过程中更好地传递梯度,从而缓解梯度消失问题。由于ReLU在正数部分斜率为1,因此梯度能够得到有效传递。
-
计算高效: ReLU函数的计算非常简单,只需比较输入和零的大小即可。相比于其他激活函数,如Sigmoid和Tanh,ReLU函数的计算速度更快,更适合在大规模神经网络中使用。
下面验证一下relu对全连接层1的输出的激活结果,使用一下代码
import torch
data = torch.tensor([[-0.0862, 0.1165, -0.1784, -0.0227, 1.4657]])
relu_data = torch.relu(data)
print(relu_data)
out1的结果
tensor([[0.0000, 0.1165, 0.0000, 0.0000, 1.4657]])
然后再进行第二个全连接层样本特征输出。全连接层2的权重也是根据第二个nn.Linear随机生成的,如下:
全连接层2-nn.linear的权重参数: Parameter containing:
tensor([[-0.3870, -0.2549, -0.4185, 0.3972, 0.2011],
[ 0.1088, -0.0173, 0.1252, 0.0926, 0.1368]], requires_grad=True)再进行前面的矩阵乘法,输出结果为
全连接层2的输出值: tensor([[0.2651, 0.1984]], grad_fn=<MmBackward0>)
最终输出值 tensor([[0.2651, 0.1984]], grad_fn=<MmBackward0>)这就是最终输出的两个值,也就是代表两个特征,这个把一开始的三个特征进行了线性和非线性的变换,最终得到两个特征
将输入的3个特征通过一个权重矩阵映射到2个输出特征,其中每个输出特征都是由输入特征经过不同的线性组合得到的。
因此,不存在特征“丢失”的情况。在这里,每个输出特征都是由输入特征的不同线性组合得到的,因此它们可能包含输入特征的不同部分。
权重矩阵的设定通常是在模型训练过程中学习得到的。具体来说,在使用 nn.Linear 建立线性层时,PyTorch 会自动为该层创建一个可训练的参数 weight,并将其随机初始化。