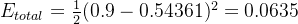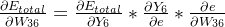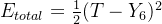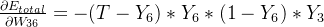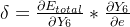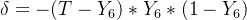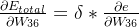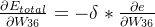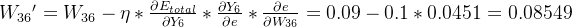一.反向传播理论简介
反向传播(Backpropagation)是神经网络中一种常用的训练算法,用于根据给定的输入和期望输出来调整网络的权重,以使网络能够更好地逼近期望的输出。
反向传播算法的基本思想是通过计算输出误差对网络中各个权重的偏导数,然后根据这些偏导数调整权重,使得网络的输出误差逐渐减小。它使用了链式法则来计算网络中每个神经元的偏导数。
以下是反向传播算法的基本步骤:
-
正向传播:将输入样本通过网络的前向传递,计算出网络的输出。
-
计算误差:将网络的输出与期望的输出进行比较,计算出网络的输出误差。
-
反向传播误差:从输出层开始,根据误差的链式法则,逐层计算每个神经元的误差贡献。
-
计算权重调整量:根据每个神经元的误差贡献,计算每个权重的调整量。通常使用梯度下降法则来计算权重调整量,即将每个权重按照其梯度方向进行微小的调整。
-
更新权重:将计算得到的权重调整量应用于网络中的权重,更新它们的数值。
-
重复以上步骤:重复执行步骤1到步骤5,直到网络的输出误差达到可接受的范围或达到预定的训练轮数。
上面的2,3,4,5,6都是我今天要讲的点
反向传播算法的关键在于通过链式法则计算每个神经元的误差贡献,并根据这些误差贡献来调整权重。它使得神经网络能够学习如何将输入映射到期望的输出,并且可以处理大量的训练样本以提高网络的泛化能力。
反向传播算法通常结合使用梯度下降法则来进行权重的调整。梯度下降法则是一种基于优化的方法,通过沿着误差曲面的负梯度方向进行迭代,以找到误差最小的权重值。反向传播算法利用了梯度下降法则来计算权重调整量,从而优化神经网络的性能。
反向传播是一种通过计算输出误差的梯度,并将该梯度反向传播到网络中的每个神经元来调整权重的训练算法。它是神经网络中常用的学习算法,被广泛应用于各种任务,如图像识别、自然语言处理等。
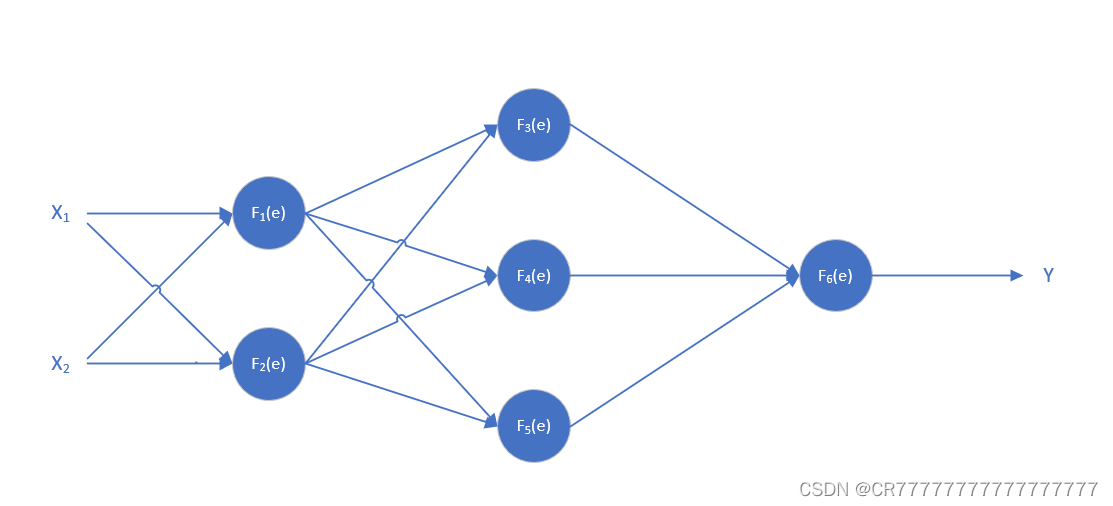
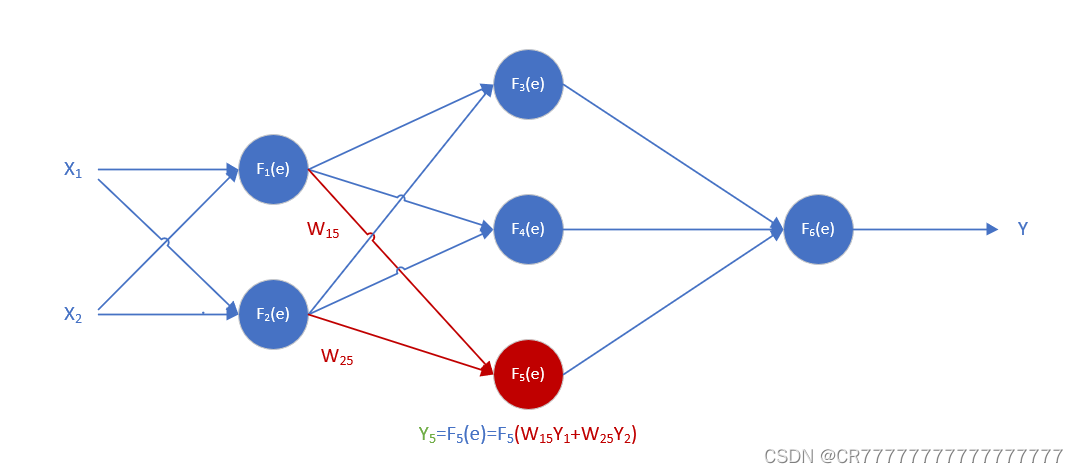
二.简单的神经网络来解释什么是前向传递,同时也可以参考我上一篇文章。
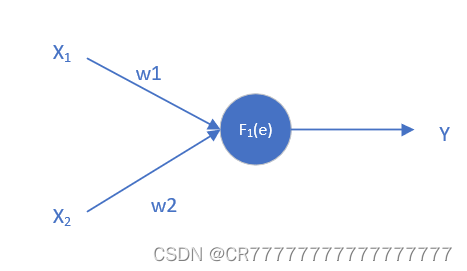
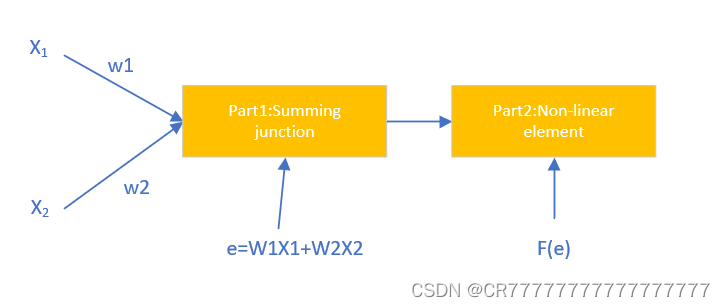
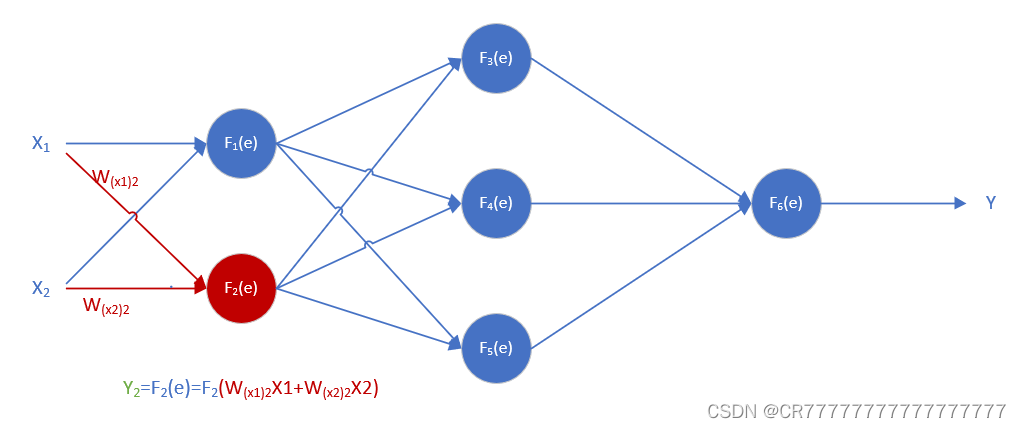
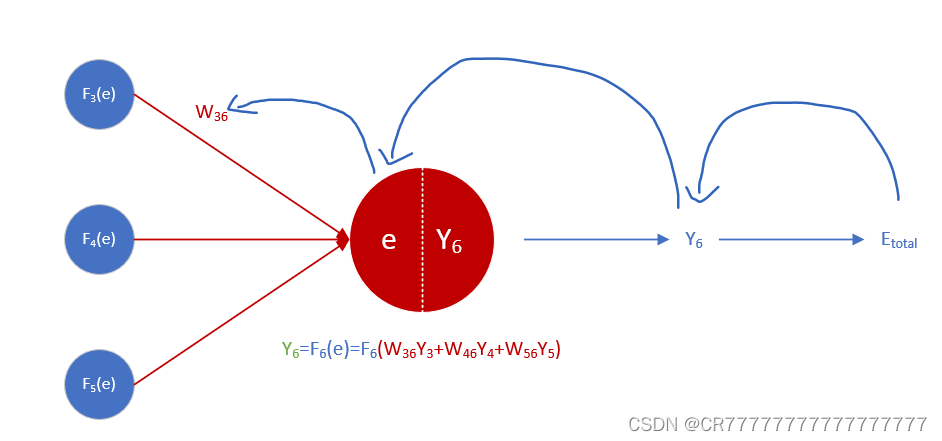
这是一个简单的三层神经网络X1和X2都是输入的数据,每个蓝色球就代表一个神经元,而每个神经元是由两个部分组成,一个是输入值X和权重系数W的线性方程,即表示为e=WX+b,b是偏置,在我的示例中我把所有偏执b都设置成0,方便理解什么是反向传播;另一部分是激活函数F(e),这样能够使得每一个神经元的输出能够呈非线性,图中的每一根连线都表示一个权重W,这些权重一般都是随机的,可大可小。
上图等价于:
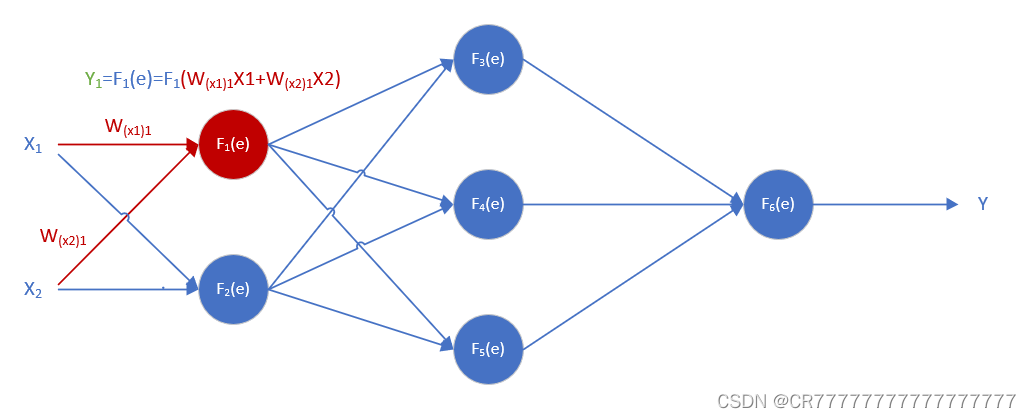
二.为了方便理解,下面详细描绘一下前向传播过程。
在此处我定义一下整个神经网络各个部分的函数,
输入值X1=2,X2=4,标签值(真实值)T=0.9
W(x1)1=0.01,W(x2)1=0.02,
W(X1)2=0.05,W(x2)2=0.08,
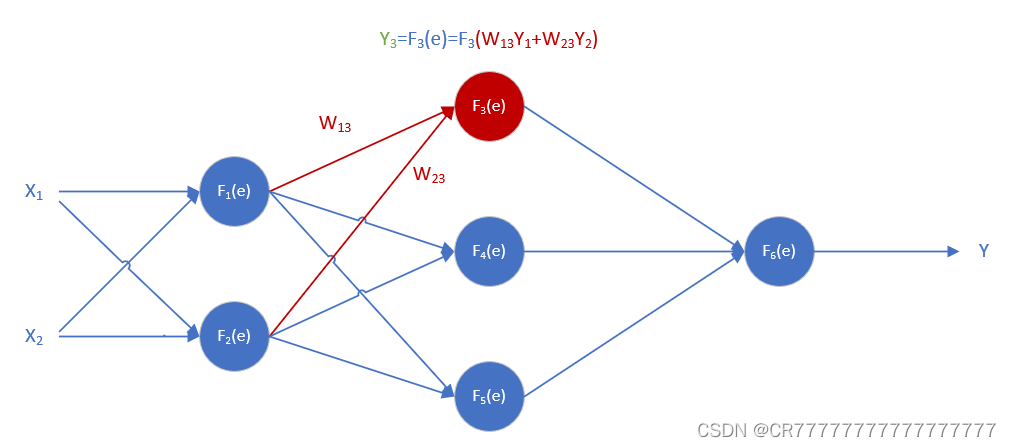
W13=0.03,W23=0.04,
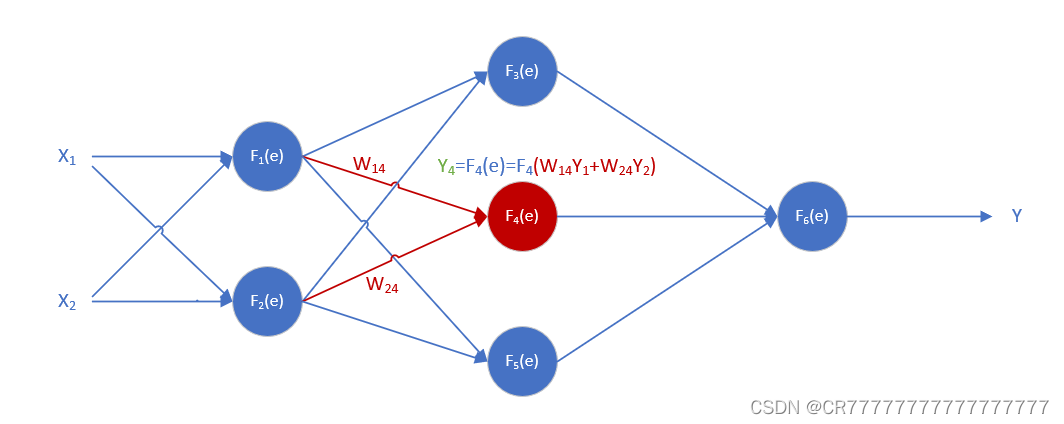
W14=0.05,W24=0.06,
W15=0.07,W25=0.08,
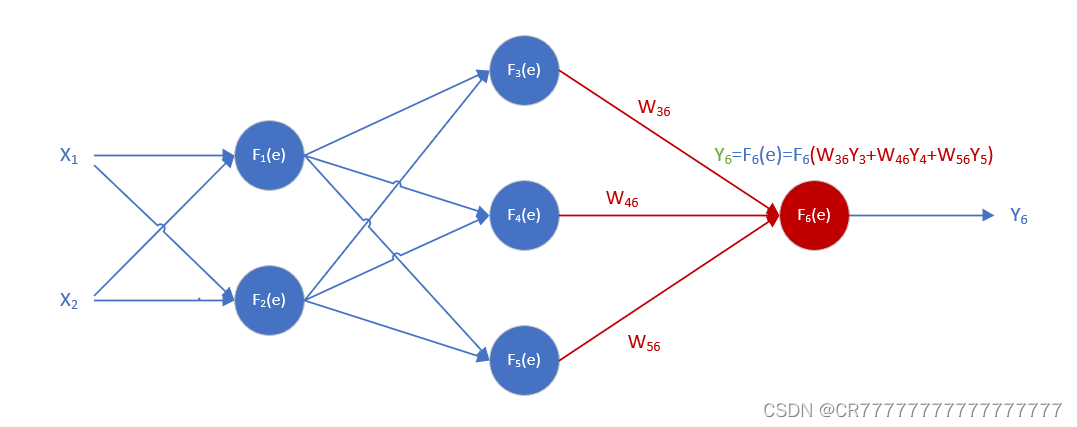
W36=0.09,W46=0.1,W56=0.15
这几个参数我都是按顺序定义的为了方便计算,实际上都应该是随机的,这里仅用作示范
激活函数Sigmoid函数:
这里计算出第一个神经元的第一部分输出为e=0.01*2+0.02*4=0.1
第二部分即为激活函数,可以得到第一个神经元的输出输出Y1==0.52498
同理e=0.05*2+0.08*4=0.42
Y2=0.60348
开始隐藏层的分析
e=0.03*0.52498+0.04*0.60348=0.0399
Y3=0.50997
e=0.05*0.52498+0.06*0.60348=0.06246
Y4=0.50615
Y5=0.52124
最后一个输出层
e=0.09*0.50997+0.1*0.50614+0.15*0.52124=0.1748973
Y6=0.54361
到了这里,神经网络的前向传播过程就已经完成了,最后输出的Y就是Y6,但是这个Y6只是前向神经网络计算出来的预测结果,并不一定是准确值(真实的标签值T,也就是咱们标定的时候标定的那个数值,例如坐标的值)
因此,最终输出的预测结果Y6与T是有一定出入,把这个出入记作θ=T-Y6。
下面我们引入损失函数这个概念,损失函数的作用是衡量模型的预测结果与目标值之间的差异或损失程度(即我们上面所说的误差θ=T-Y)。在训练机器学习模型的过程中,我们希望通过调整模型的参数W来使得模型的预测结果尽可能接近目标值。最常见的损失函数就是最小二乘法损失函数:1/2∑(目标值 - 预测值)²。即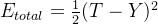
所以这里的总误差
我们现在开始进行反向传播,反向传播的目的是为了更新权重W,至于每个权重W对最后的误差θ造成了多少影响,可以用整体误差对W36求偏导得出:这是根据链式法则得到的
下面我分别计算上面链式当中的最后一个偏导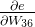
第二个偏导就是对Sigmoid函数求导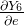
(这个分母中的底数e是自然对数的底数,指数这个e表示每个神经元的e=0.17489)
上面这一行的e就是指的神经元的e
最后计算就是第一个偏导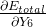
这是计算最小二乘法的导数,
最后三者连乘
到这里我们就计算出整体误差Etotal对w36的偏导值,这个值的含义就是指这个参数都最后整体误差的影响程度(叫做梯度值),可正可负。
把上面这个求偏导的过程可以简化成一个公式:
为了方便,我这里把每个神经元的输出误差用δ来表示
所以对W36的偏导可以用这个来表示:
如果偏导为负数,可以加个符号:
所以我们对W36的梯度值为0.0451
最后可以设置学习率η来更新参数W36,这里设置成0.1
因此更新后的W36为:
这就是对一个前向传播中的某个参数进行梯度更新的过程,当然这个更新过程不可能是一次完成的,在进行完一次反向传播更新梯度后紧接着会进行下一个前向传播,然后重新计算误差,这样多次循环之后会使得损失值逐渐降低,当达到某个设定值时这个循环更新梯度的过程就会停止,从而完成一整个训练流程。
如果有何错误欢迎指正,如果有引用请注明出处!后续会对这篇文章继续完善,会将验证损失是否降低以及一个完整的梯度更新流程补充好~