目录
浮点数存储规则
根据国际标准IEEE754(电气和电子工程协会)规定:任意一个 浮点数F的二进制 都可以表示成以下形式:科学计数法
(-1)^S * M * 2^E
解析科学计数法:
1.解析:(-1)^S
(-1)^S 表示的是 浮点数F 的 符号位
当 S = 0 时,原式 = (-1)^0 = 1,此时的 1 就表示 浮点数F 为 正数
当 S = 1 时,原式 = (-1)^1 = -1,此时的 -1 就表示 浮点数F 为 负数
2.解析:M
M 表示 有效数字,且 M 的取值范围是:M >= 1 && M < 2
3.解析:2^E
2^E 表示 指数位,E 的取值为:有效数字M 的 小数点 的 移动位数
举例说明:浮点数5.5 如何表示成 科学计数法
1.十进制的浮点数5.5 如何转换为 二进制:
整数部分的 5 转换为 二进制 为:101 ---> 1*2^2 + 0*2^1 + 1*2^0 = 4 + 0 + 1 = 5
小数部分的0.5 转换为 二进制 为: 0.1 ---> 1*2^(-1) = 0.5
合并:浮点数5.5 转换成 二进制 为:101.1
2. 浮点数5.5 表示为 科学计数法
F = 5.5 = (-1)^0 * 1.011 * 2^2
其中:S = 0;M = 1.011;E = 2
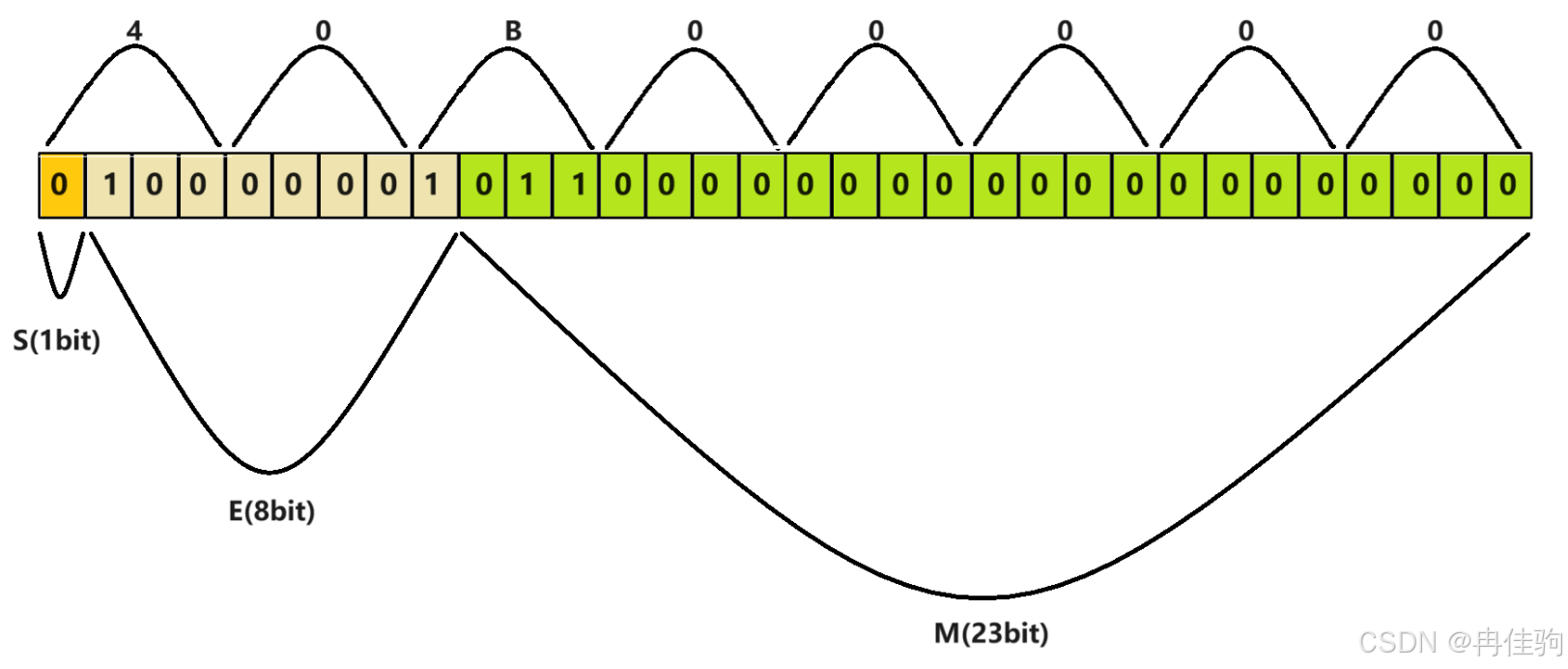
单\双精度浮点数 存储 S、M、E 的布局
由以上结论可以得出:只要有 S、M、E 这三个数时,就能 还原浮点数F
所以 IEEE754规定:在 内存中存储浮点数 时,存储的是 S、M、E 这三个数
单精度浮点数存储 S、M、E 的布局:
最高位存储的是 符号位S,后面的 8个bit位 存储的是 指数位E,剩下的 23个bit位 存储的是 有效数字M
单精度浮点数存储 S、M、E 的布局:
最高位存储的是 符号位S,后面的 11个bit位 存储的是 指数位E,剩下的 52个bit位 存储的是 有效数字M
有效数字M 和 指数位E 的特殊规定
有效数字M 的特殊规定:
M 的取值范围:M >= 1 && M < 2
那么 M 的表示形式:1.xxxxxxxx,其中 xxxxxxxx 为小数部分
所以 IEEE754 规定:省去 小数点前面 的 1,在内存 中 只保存小数点后面 的 部分,等到 读取 的时候,再把 小数点前面 的 1 加上
举例说明:M = 1.011
那么在内存中只会存储 011,只有等到 读取时加上 小数点前面的 1
指数位E 的特殊规定:
IEEE754 规定:指数位E 是一个 无符号整数(unsigned int )
但 指数位E 在实际情况下 会 有为 负数 的情况:
如:浮点数0.5 转换为 二进制为:0.1
F = 0.5 = (-1)^0 * 1.0 * 2^(-1) ;此时的 指数位E 就为 -1
所以为了规避这种情况:
IEEE754 规定:指数位E 存入内存时的真实值 必须再加上一个中间数
中间数值 的规定:
对于 8个bit的E(单精度浮点数),中间数是127
对于 11个bit的E(双精度浮点数),中间数是1023
浮点数在内存中是否存储的S、M、E
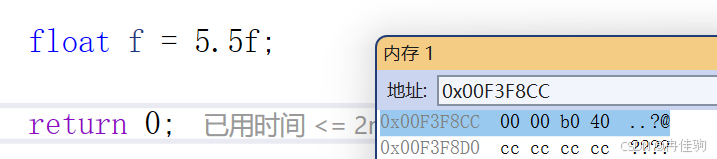
创建 浮点数变量,调试代码,查看 浮点数 在内存 中 存储的模式即可
代码演示:
float f = 5.5f;代码解析:
浮点数默认为 double类型,所以要在 5.5 后面加一个 f,用来强调 5.5 是 float类型
浮点数f 表示为科学计数法:
f = 5.5 = (-1)^0 * 1.011 * 2^2
S = 0
M = 1.011 ---> M只存储小数点后的有效位:011
E = 2 ---> E+127 = 129(float为单精度浮点类型)
浮点数f 的 S、M、E 在内存中表示形式:
S = 0;转换为二进制:0
M = 011;
E = 129;转换为二进制:1000 0001(记住:E是无符号整数,所以最高位是有效位)
转换为内存示意图如下:
大小端存储的相关知识请见:C语言 ——— 大/小端存储模式的介绍及判断-CSDN博客
那么 浮点数5.5 以 十六进制的形式 在 内存中 以 小端字节序存储 为:00 00 B0 40
代码验证: