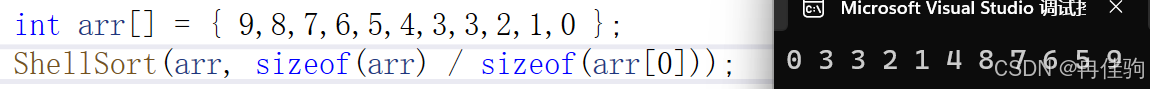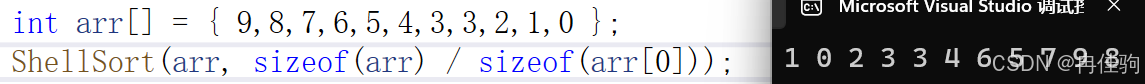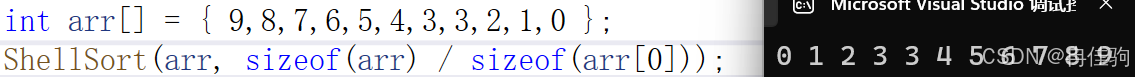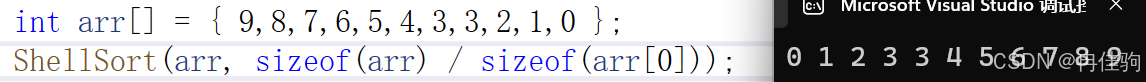目录
前言
在上一章学习了直接插入排序算法的实现
接下来要学习的是希尔排序,是在直接插入排序算法上优化的排序
希尔排序算法的思想
第一步:先预排序
预排序也就是把数组排成接近有序的状态
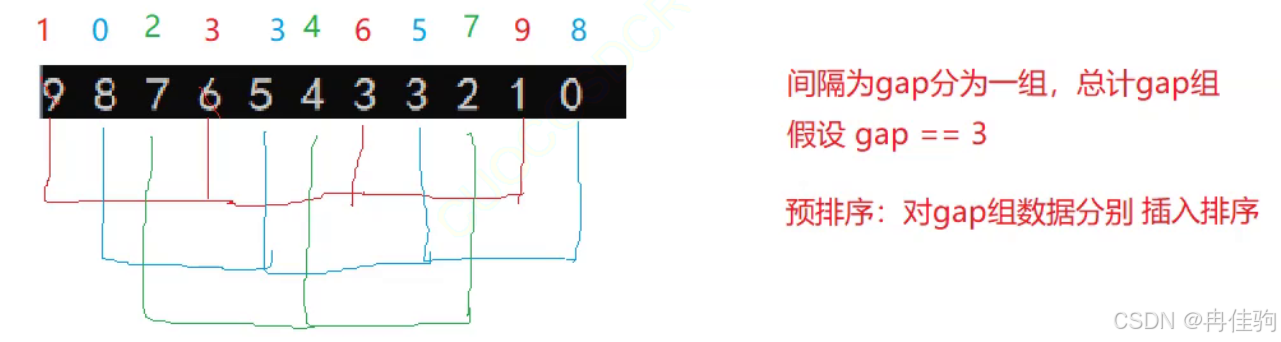
预排序的步骤:间隔为 gap 的长度分为一组,总计 gap 组,gap 的大小根据数组的长度改变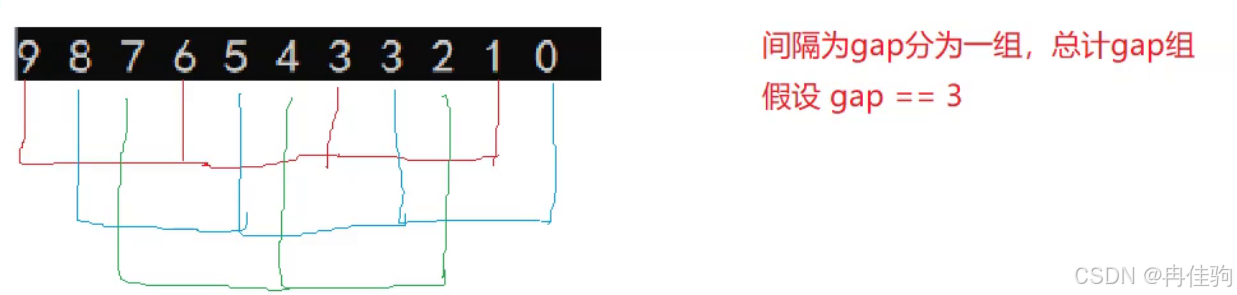
举例来说:9,6,3,1 为一组,那么就对这一组排序
排好后的结果就是 1,3,6,9 (默认升序)
其他各组和举例相同,最后预排序的结果如下
第二步:再直接插入排序
对数组预排序完成后,数据就是接近有序的状态了,这时再对数组进行直接插入排序即可
注意:第二步并不是调用直接插入排序函数,而是通过预排序的代码进行优化直接得出希尔排序,详情请见以下代码
代码实现(默认排升序)
预排序思路的代码
代码演示:
int gap = 3; //待定
for (int i = 0; i < size - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}代码解析:
gap 的具体大小还需待定,先通过 a[] = { 9,8,7,6,5,4,3,3,2,1,0 },这组数据来举例说明
以上预排序代码的核心逻辑类似于直接插入排序算法
不同之处在于直接插入排序算法的 a[end] 和 tmp 间隔了 1
而预排序的 a[end] 和 tmp 间隔了 gap
这也就实现了相同颜色为一组,各自进行预排序
需要注意控制变量 i 的大小,防止越界
代码验证:
当 gap == 5 时:
当 gap == 3 时:
当 gap == 1 时:
结论:
当 gap 越大时,说明间隔越大,越不接近有序
当 gap 越小时,说明间隔越小,越接近有序
当 gap 为 1 时,就是直接插入排序算法,因为直接插入排序算法的 a[end] 和 tmp 的间隔就是 1
所以可以得出,想要将预排序直接优化成希尔排序,那么就要控制 gap 的大小
希尔排序算法的代码实现
代码演示:
void ShellSort(int* a, int size)
{
int gap = size;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < size - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}代码解析:
gap 初始值赋值为数组元素总个数的大小 size
每次循环 gap = gap / 3 + 1
+1 的作用是为了保证 gap 最后一次能被赋值为 1,因为 gap 为 1 时就是直接插入排序,这样做的作用避免了调用直接插入排序算法的函数,且在一个逻辑里面就对数组直接排好了序
当 gap == 1 时,进行预排序后,此时数组就是有序状态了,所以最外部的 while 循环判断 gap > 1 即可完成排序
代码验证: