系列文章戳这里👇
- 什么是上下文无关文法、最左推导和最右推导
- 如何判断二义文法及消除文法二义性
- 何时需要消除左递归
- 什么是句柄、什么是自上而下、自下而上分析
- 什么是LL(1)、LR(0)、LR(1)文法、LR分析表
- LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系
- 编译原理第三章习题
- 词法分析、构建DFA、上下文无关文法、LL(1)分析、提取正规式
- 证明LL(1)、SLR(1)、LALR(1)文法
- 翻译方案、属性栈代码
- 【运行时环境】什么是活动记录、 活动记录与汇编代码的关系
如何判断二义文法
给定一个文法 G G G,如果这个文法 G G G的一些句子中存在不止一棵分析树,或者这些句子存在不止一种最左(最右推导), 我们就称该文法为二义性的, G G G也叫二义性文法。
注意:文法二义并不代表语言一定是二义的,只有当产生一个语言的所有文法都是二义时,这个语言才成为二义的。
举个栗子
S
→
a
S
b
S
∣
b
S
a
S
∣
ϵ
S→aSbS\ |\ bSaS\ |\ \epsilon
S→aSbS ∣ bSaS ∣ ϵ
(
a
)
(a)
(a)为句子
a
b
a
b
abab
abab构造两个不同的最左推导,以此说明该文法是二义的
第一种最左推导:
S
→
a
S
b
S
→
a
b
S
a
S
b
S
→
a
b
a
S
b
S
→
a
b
a
b
S
→
a
b
a
b
S→aSbS→abSaSbS→abaSbS→ababS→abab
S→aSbS→abSaSbS→abaSbS→ababS→abab
第二种最左推导:
S
→
a
S
b
S
→
a
b
S
→
a
b
a
S
b
S
→
a
b
a
b
S
→
a
b
a
b
S→aSbS→abS→abaSbS→ababS→abab
S→aSbS→abS→abaSbS→ababS→abab
因此该文法是二义的
如何消除文法二义性
举个栗子
有下列描述命题演算公式的二义文法,为它写一个等价的非二义文法
S
→
S
a
n
d
S
∣
S
o
r
S
∣
n
o
t
S
∣
p
∣
q
∣
(
S
)
S→S\ and\ S|S\ or\ S|not\ S|\ p\ |\ q\ |(S)
S→S and S∣S or S∣not S∣ p ∣ q ∣(S)
由于该文法没有体现算符
a
n
d
、
o
r
、
n
o
t
and、or、not
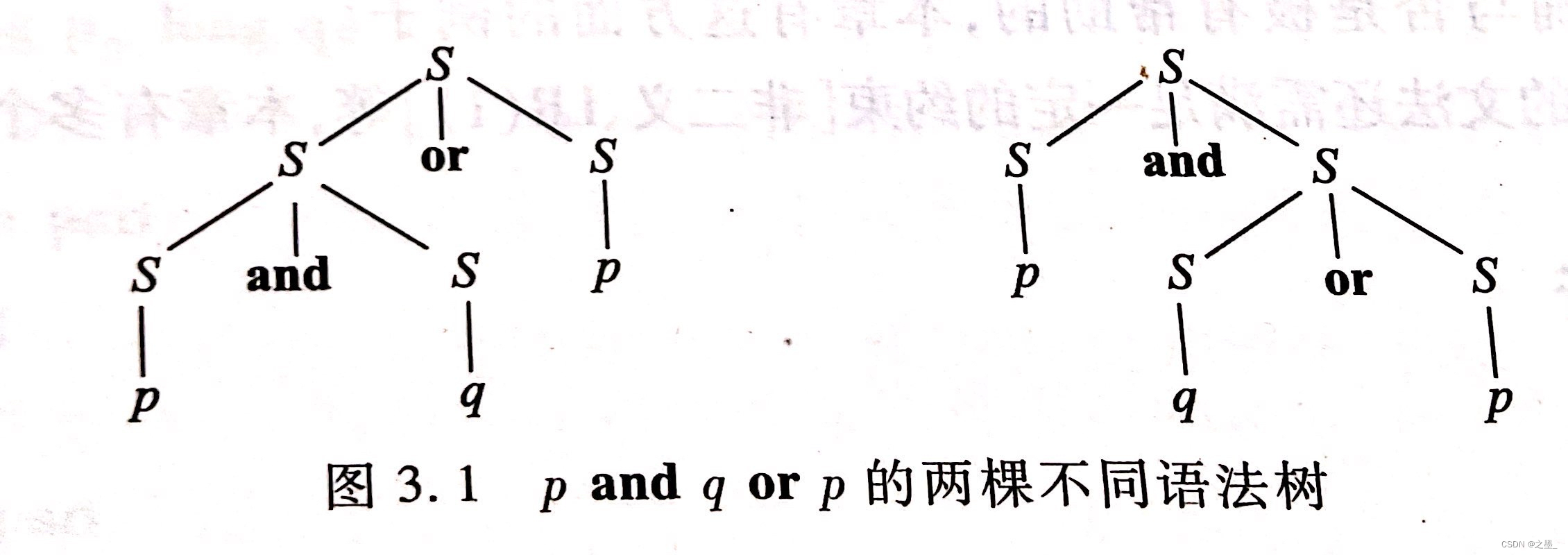
and、or、not的优先次序和结合规则,因此该文法二义。如
p
a
n
d
q
o
r
p
p\ and\ q\ or\ p
p and q or p可以分解成两个子表达式,见下图的两棵不同语法树。
从我的理解来看,消除二义性,无非就是体现出各算符的优先次序,因此我总结如上形式的消除二义方法如下:
- 将最低优先级的运算提至第一层产生式
- 最后一层上的各层产生式添加 ′ ∣ ′ '|' ′∣′单独推导向下一层
- 其余按照优先级高低逐层向下写
- 使用新的非终结符代替原终结符
- 最后一层产生式要能够推回第一层产生式
则上述二义文法消除二义性如下
E → E o r T ∣ T T → T a n d F ∣ F F → n o t F ∣ p ∣ q ∣ ( E ) E→E\ or\ T\ | \ T\\ T→T\ and\ F\ |\ F\\ F→not\ F|\ p\ |\ q\ |(E) E→E or T ∣ TT→T and F ∣ FF→not F∣ p ∣ q ∣(E)
做一个简要的解释
因为 o r or or的优先级是最低的, n o t not not最高,所以第一层是 o r or or运算的产生式,可以看到最后一层存在 ( E ) (E) (E),括号保证了 o r or or运算的分解是唯一的
以下是书本中的解释
再举个栗子
改写二义文法
E
→
E
+
E
∣
E
∗
E
∣
(
E
)
∣
−
E
∣
i
d
E→E+E | E*E |(E)| -E | id
E→E+E∣E∗E∣(E)∣−E∣id
优先级从低到高:
[
+
]
;
[
∗
]
;
[
(
)
,
−
,
i
d
]
[+];[*];[( ), -, id]
[+];[∗];[(),−,id]
结合性:
左结合:
[
+
,
∗
]
[+, *]
[+,∗]
右结合:
[
−
]
[-]
[−]
无结合:
[
i
d
]
[id]
[id]
非终结符与运算:
E
:
+
E:+
E:+(
E
E
E产生式,左递归)
T
:
∗
T:*
T:∗(
T
T
T产生式,左递归)
F
:
−
,
(
)
,
i
d
F:-,( ),id
F:−,(),id (
F
F
F产生式,右递归)
得到:
E
→
E
+
T
∣
T
T
→
T
∗
F
∣
F
F
→
(
E
)
∣
−
F
∣
i
d
E → E + T | T\\ T → T * F | F\\ F → (E) | -F | id
E→E+T∣TT→T∗F∣FF→(E)∣−F∣id
何时要消除二义性
有些类型的分析器,它希望处理的文法是无二义性的,否则它不能唯一确定对某个句子应选择哪棵分析树。出于某些需要也可以构造允许二义文法的分析器,不过这样的文法要附带消除二义性的规则,以便分析器扔掉不希望的分析树,为每个句子只留一棵分析树。
但大多数编程语言都不用无二义的文法,而是采用二义文法,因为一般来讲,二义文法较无二义文法会更加简洁(下面的例子可以让你看到这一点)。定义语言语法的文法有二义性并不可怕,只要有消除二义性的规则就可以了。
并且,LL(1)文法既不是二义性的,也不含左递归,在什么是LL(1)、LR(0)、LR(1)文法有相关介绍。